四連桿膝關節假肢的動力學建模與分析1)

呂 陽 方虹斌 徐 鑒 馬建敏 王啟寧 張曉旭

(復旦大學航空航天系，上海 200433)

(復旦大學智能機器人研究院，上海 200433)

(上海智能機器人工程技術研究中心，復旦大學，上海 200433)

(智能機器人教育部工程研究中心，復旦大學，上海 200433)

(北京大學工學院，北京 100871)

引言

根據全國第二次殘疾人抽樣調查的結果[1]，我國肢體殘疾2412 萬人，占殘疾人總數的29.07%，其中下肢截肢患者大概有158 萬人.為了使大腿截肢患者能夠正常地生活和工作，越來越多的研究者開始致力于假肢的結構設計與優化研究.

膝關節假肢在結構上可分為單軸式膝關節和多軸式膝關節.單軸式膝關節具有結構簡單、可靠性高的優點，其代表性產品主要有奧托博克公司的CLeg、奧索公司的Rheo Knee 等[2].多軸式膝關節如四連桿膝關節則具有良好的仿生特性[3]，能夠較為真實地逼近人體膝關節轉動瞬心(小腿相對大腿轉動時的速度瞬心，簡稱轉動瞬心)的J 形軌跡，其代表性產品主要有奧索公司的Parso Knee、北京工道風行公司的K301 等.值得一提的是，近年來，折紙結構由于其結構輕、可編程以及超材料特性被廣泛研究，這些特性在膝關節的J 形軌跡實現上也有一定的應用潛力[4].在運動性能上，J 形軌跡意味著小腿假肢在站立時的瞬心較高，從而實現較好的穩定性；在擺動時的瞬心較低，有較好的靈活性[5].因此，相比于單軸式膝關節，四連桿膝關節兼顧運動穩定性，具有更好的運動性能.

為了對四連桿膝關節的運動性能有更好的認識，需要明確影響其運動性能的因素.從動力學的角度來看，影響運動性能的因素包括足--地交互作用力、膝關節單邊約束產生的強非線性作用力、液壓阻尼器提供的彈性回復力及阻尼力等.要明確各因素對假肢性能的影響機制，就必須建立考慮足--地交互作用力和膝關節單邊接觸力的一體化動力學模型，并就該模型產生的動力學響應進行分析.

目前，對于假肢的建模，常用的建模方法是利用第一類拉格朗日方程.這種方法將假肢運動階段分為站立相(假肢與地面接觸，處于站立狀態)和擺動相(假肢未與地面接觸，處于擺動狀態)，對不同的步態階段分別進行建模[6-10].在站立相階段，該方法將足--地接觸簡化為理想鉸接約束，通過在動力學方程中引入拉格朗日乘子求解模型；在膝關節存在單邊約束時，假設大腿和小腿為一根剛性桿，引入拉格朗日乘子對模型進行求解.這種建模方法未對足--地交互作用力以及膝關節單邊接觸力直接進行建模，而是基于假設將這兩種力看作理想約束力.實際上足--地交互作用力以及膝關節單邊接觸力等強非線性因素為非理想約束力，上述處理方式無法體現這一點，因此需要運用更合理的方式對這兩種力進行建模.

足--地交互作用力本質上是足--地接觸時產生的接觸力和摩擦力，膝關節單邊接觸力本質上是膝關節連桿間限位碰撞產生的接觸力，因而其建模方式可以借鑒多剛體動力學對接觸力和摩擦力的描述.接觸力模型中有赫茲接觸力模型[11]以及改進的赫茲接觸力模型[12].赫茲接觸力模型形式相對簡單，但不考慮能量耗散，不適用于真實的接觸情況；改進的赫茲接觸力模型通過各種方式加入了能量耗散項，常用的有Hunt-Crossley 模型[13]、Gonthier 模型[14]、Kelvin-Voigt[15]模型等，更適用于真實的接觸情況.摩擦力模型主要包括：庫倫摩擦模型[16]、Stribeck 摩擦模型[17-19]以及更為復雜的LuGre 摩擦模型[20-23].實驗研究[24-27]表明，當剛體相對運動尺度為毫米量級或更高時，若要分析摩擦對系統動力學行為的影響，采用庫倫摩擦模型即可達到足夠高的精度.為解決庫倫摩擦模型中非光滑本構對動力學分析帶來的困難，還可進一步利用非線性函數[28]對庫倫摩擦模型進行光滑化.近年來，基于上述接觸和摩擦模型的雙足行走機器人[29-32]動力學分析已經取得一定進展，但基于上述接觸和摩擦模型的假肢動力學分析仍處于起步階段.

綜上所述，足--地交互作用力以及膝關節單邊接觸力等強非線性因素對假肢步態的影響尚未得到深入分析，其難點在于考慮足--地交互作用力和膝關節單邊接觸力的一體化動力學建模.針對該問題，基于多剛體動力學中關于接觸力及摩擦力的研究，本文將采用Kelvin-Voigt 模型和庫倫模型描述足--地接觸力和摩擦力，采用Kelvin-Voigt 模型描述膝關節單邊接觸力，從而基于第一類拉格朗日方程對四連桿膝關節被動假肢進行動力學建模.將步態實驗測得的髖關節運動數據作為動力學模型的驅動信號，四連桿膝關節被動假肢的步態可以通過數值計算得到.進一步，為了評價假肢步態與健康人實測步態的一致性，本文定義了步態相關系數作為評價指標，并分析四連桿膝關節液壓阻尼器剛度、阻尼參數對相關系數的影響.

本文的貢獻和創新點在于：首先，進一步完善四連桿膝關節假肢的動力學模型，重點關注足--地交互作用力以及膝關節單邊接觸力等強非線性因素對下肢假肢步態的影響，為殘疾人行走時的代償行為提供一種新的力學解釋；其次，以實測數據為參考信號進行步態一致性評估和參數分析，為四連桿膝關節被動假肢的進一步優化提供理論支撐，提高結論的可靠性.

本文第1 節介紹四連桿膝關節假肢動力學模型的建立.首先分析四連桿的運動學特性，接著引入足--地交互作用力和膝關節單邊接觸力，最后基于第一類拉格朗日方程對假肢進行建模.第2 節介紹健康被試的步態測試.一方面，實測髖關節運動數據作為假肢動力學模型的驅動信號，用于假肢步態分析；另一方面，實測膝關節運動數據作為假肢步態運動的對比信號，用于步態一致性評估及參數分析.第3 節為基于假肢動力學模型的步態分析.將數值計算所得結果與實驗測得的步態進行比較，討論四連桿液壓阻尼器剛度、阻尼參數對步態周期失諧及步態一致性的影響.第4 節給出研究結論.本文通過數值計算研究了四連桿膝關節被動假肢動力學模型的響應，分析了四連桿膝關節液壓阻尼器的阻尼、剛度參數對假肢步態指標的影響，總結了提高步態性能的一般經驗，以期為四連桿膝關節被動假肢的參數設計提供參考依據.

1 四連桿膝關節被動假肢動力學模型

四連桿膝關節被動假肢具有良好的仿生特性，但由于結構更為復雜，足--地交互作用力、膝關節單邊接觸力等強非線性因素會導致下肢假肢產生更為豐富的動態響應，進而在整體上影響步態的周期性和穿戴舒適性.因此，本文有必要從動力學角度對四連桿膝關節假肢進行分析.

1.1 四連桿機構的運動學模型

如圖1 所示，人體膝關節由股骨踝(femoral ankle)和脛骨踝(tibia ankle)組成，依賴于股踝和脛踝接觸面的幾何外形，人體膝關節的運動屬于非定軸轉動，小腿相對于大腿轉動的速度瞬心軌跡實際是一條J 形曲線.其生物學優勢在于，在站立相時，膝關節瞬心升高，小腿相對于瞬心的轉動慣量較大，不易實現轉動，因而穩定性好；反之，在擺動相時，小腿靈活性好，這也是四連桿膝關節仿生學研究的主要動機.

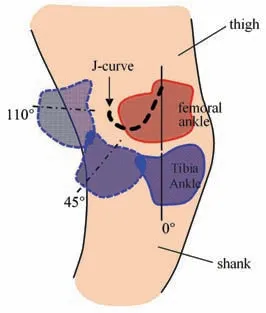
圖1 人體膝關節非定軸轉動及其J 形瞬心軌跡Fig.1 Non-fixed axis rotation of human knee joint and its J-curve of instantaneous rotation center

四連桿膝關節可以較好地模擬人體膝關節非定軸轉動過程，主要由四根連桿和液壓阻尼器組成，其結構示意圖及實物圖如圖2 所示.以工道風行公司(GDFX)設計的一款四連桿膝關節為例，其幾何參數及慣量參數如表1 所示.根據四連桿的連接關系，四連桿機構的運動約束方程可以表示為

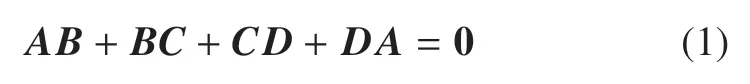
在二維笛卡爾坐標系下，式(1)可以具體表示為

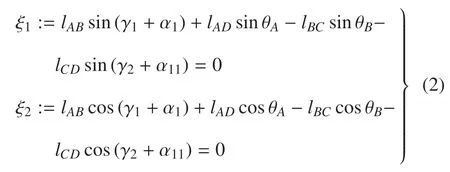
圖2 四連桿膝關節Fig.2 Four-bar linkage prosthesis knee

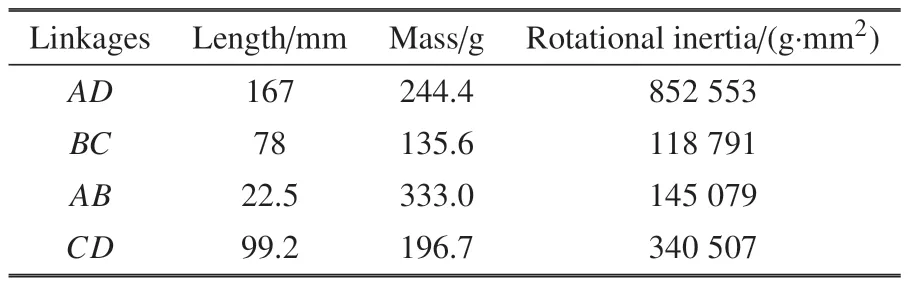
表1 四連桿膝關節物理參數表Table 1 Physical parameter values of the four-bar-linkage knee prosthesis

其中，lAB，lAD，lBC和lCD分別為連桿AB，AD，BC和CD的長度，γ1=90?為連桿AB與大腿股骨夾角，γ2=24?為連桿CD與小腿脛骨夾角，θA，θB分別為連桿AD，BC與豎直方向夾角，α1為大腿股骨與豎直方向夾角，α11為小腿股骨與豎直方向夾角.

由幾何關系可知，四連桿膝關節在轉動過程中小腿相對于大腿的瞬心P在CB和DA的延長線上.在平面笛卡爾坐標系下，瞬心P的坐標可以表示為

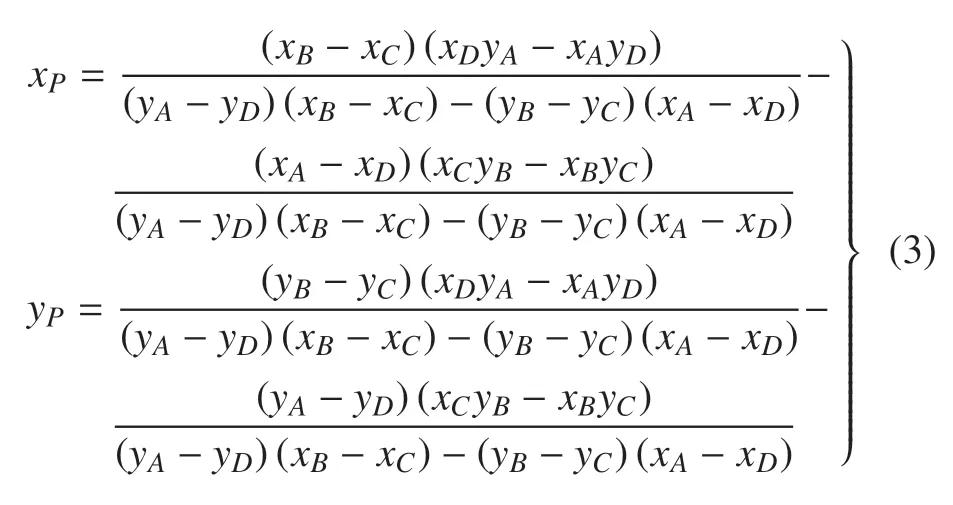
其中，xP為瞬心P的橫坐標，yP為瞬心P的縱坐標，xk和yk分別為四連桿頂點k(k=A,B,C,D)的橫坐標和縱坐標.圖3 展示了小腿相對于大腿轉動時速度瞬心P的軌跡曲線，其中假肢大腿與AB桿剛性連接，假肢小腿與CD桿剛性連接.可以看到，在膝關節由伸直狀態至110?屈曲狀態過程中，瞬心P形成的軌跡是一條J-curve 線，與人體膝關節瞬心的J 形軌跡相似，展現了良好的仿生特性.

1.2 足--地交互力和膝關節單邊接觸力模型

足--地交互作用力主要有地面對假肢足底的接觸力和摩擦力兩部分.為方便分析，本文假設只有腳跟和腳尖這兩點與地面存在接觸力和摩擦力.

地面對足底的接觸力可以通過Kelvin-Voigt 模型來描述

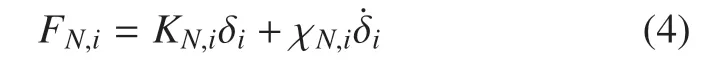
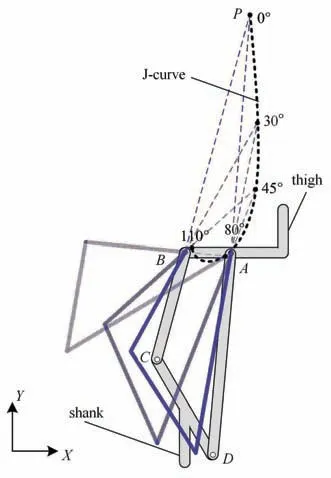
圖3 四連桿膝關節J 形瞬心軌跡Fig.3 Four-bar linkage prosthesis knee’s J-curve of instantaneous rotation center

式中，FN,i表示接觸力，方向垂直于地面，下標i為heel 或toe，分別表示腳跟和腳尖與地面接觸時接觸力的描述.KN,i表示接觸剛度，χN,i表示接觸阻尼.δi表示腳尖或腳跟與地面之間的壓痕深度，當腳尖或腳跟離地時，規定δi=0.地面對足底的摩擦力采用庫倫摩擦模型描述[16]

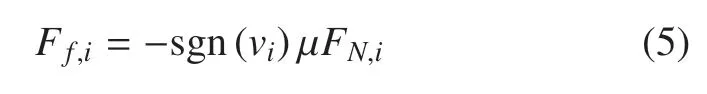
式中，Ff,i表示摩擦力，方向沿水平方向，下標i為heel 或toe，分別表示腳跟和腳尖與地面接觸時摩擦力的描述.μ表示動摩擦系數(此處忽略靜摩擦系數)，vi表示腳尖或腳跟相對地面的切向速度.為方便動力學分析，本文對式(4)所述接觸力模型和式(5)所述摩擦力進行光滑化處理，具體光滑化形式分別為

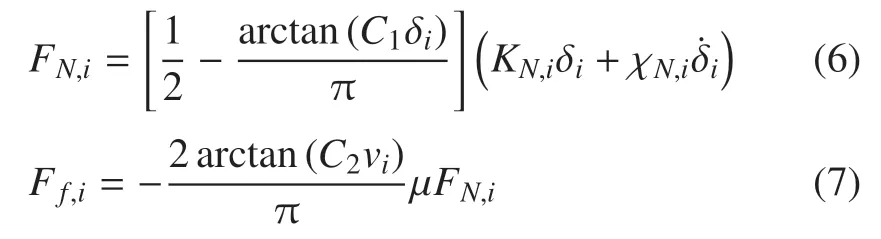
其中C1和C2為常數，表征接觸力和摩擦力的光滑化程度.

此外，如圖4 所示，當假肢小腿擺動到與大腿呈同一角度時(即膝關節打直)，為保證穿戴者安全性，四連桿的AB和BC兩桿之間將通過限位裝置鎖死，鎖死端面垂直于AB連桿.這種結構鎖死是一種單邊約束，力學上可以簡化為單邊接觸模型.因此，本文同樣通過光滑化的Kelvin–Voigt 模型來描述膝關節打直的單邊接觸力，具體形式為

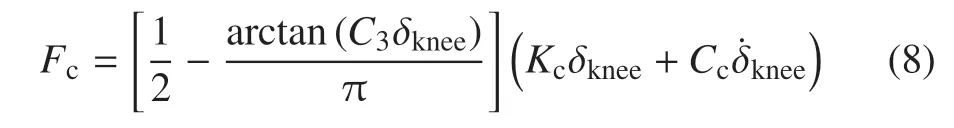
其中，Fc表示單邊接觸力，方向為AB連桿方向，Kc表示接觸剛度，Cc表示接觸阻尼，δknee表示兩桿之間的壓痕深度.需要注意的是，如圖4 中細節放大圖所示，AB和BC兩桿間限位接觸點與B點不重合，其偏心距為d=1 cm，因此式(8)所示接觸力作用于連桿BC和AB的力矩分別為

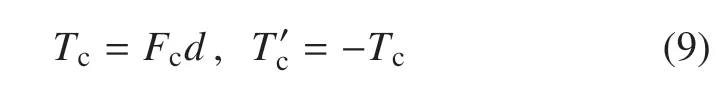
至此，本文得到了足--地交互作用力和膝關節單邊接觸力的模型.

圖4 膝關節幾何鎖死時接觸力示意圖Fig.4 The contact force when the knee is locked geometrically

1.3 基于第一類拉格朗日方程的動力學建模

假設四連桿膝關節的接受腔與殘疾人大腿殘肢為剛性連接，因此四連桿膝關節被動假肢的運動模型可簡化為圖5 所示形式.其中x和y分別為髖關節在平面笛卡爾坐標系下的橫坐標和縱坐標，α1為大腿與豎直方向的夾角，α11為小腿與豎直方向夾角，β1為足部與水平方向夾角.

如圖5 所示，四連桿機構中的液壓阻尼器主要是在運動過程中提供阻尼力和回復力，其合力可以表示為

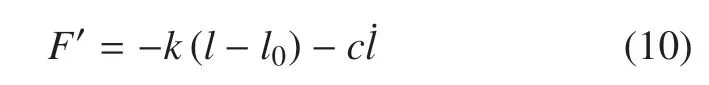
式中，k和c分別為液壓阻尼器的剛度和阻尼系數，l0=168.79 mm 為液壓阻尼器原長，l為當前長度.基于虛功原理，合力F0作用于廣義坐標θ1上的廣義力為

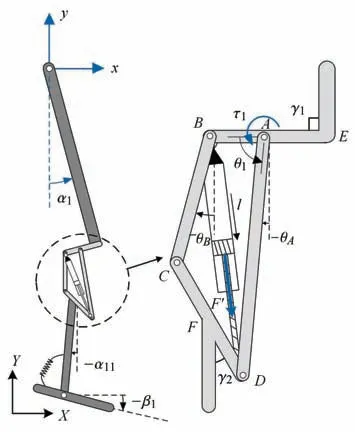
圖5 四連桿膝關節被動假肢運動模型Fig.5 Model of passive four-bar linkage prosthesis knee

此外，由于θ1=0.5π ?α1+θA，因此合力F0作用于廣義坐標α1和θA上的廣義力矩分別為?τ1和τ1.

此外，本文假設踝關節受到帶阻尼的扭簧作用，作用力矩表示為

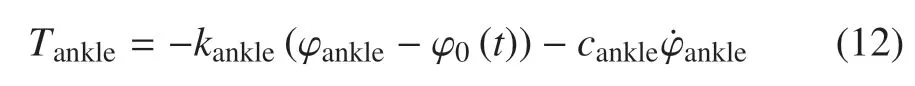
其中，kankle=10 N/m 和cankle=0.2N/(m·s?1)分別為扭簧的剛度和阻尼系數，為踝關節角度，為踝關節期望角度.在步態分析中，本文以實測踝關節角度作為.由圖5 可知，踝關節角度滿足=β1?α11，因此扭簧作用于廣義坐標α11和β1的扭矩分別為?Tankle和Tankle.

得到基于四連桿約束的運動學模型、足--地交互力和膝關節單邊接觸力模型后，圖5 所示的四連桿膝關節被動假肢的動力學模型可以用第一類拉格朗日方程表示

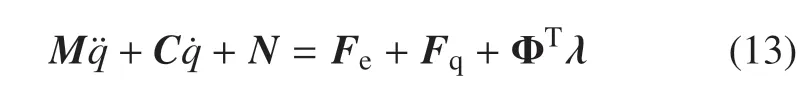
式中，q=(x,y,α1,α11,θA,θB,β1)T為廣義坐標向量，是質量陣，是科氏力和離心力項，是重力項.M(q),及N(q)中各元素表達式見附錄A.Fe為足--地交互作用力和膝關節單邊接觸力構成的廣義力向量，具體表示為

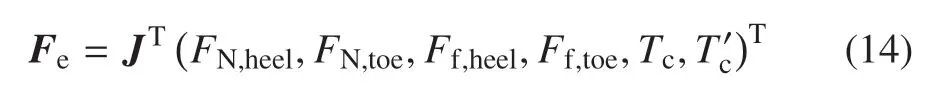
其中，FN,heel和FN,toe由式(6)給出，Ff,heel和Ff,toe由式(7)給出，Tc和由式(9)給出，J為將足--地交互作用力和膝關節單邊接觸力變換為廣義力的Jacobi 矩陣，具體形式見附錄A.Fq為膝關節的液壓阻尼器和踝關節的阻尼彈簧施加的廣義力向量，具體表示為

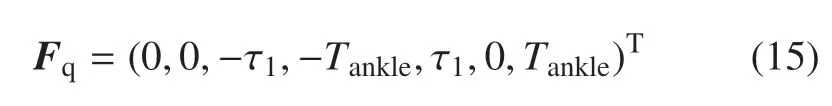
其中，τ1由式(11)給出，Tankle由式(12)給出.Φ 為四連桿約束矩陣，具體表示為

其中，ξ1和ξ2為式(2)所示約束方程.λ 為拉格朗日乘子，表示四連桿約束產生的約束力.

需要指出的是，被動假肢是由髖關節運動驅動的，髖關節運動信號x，y，α1為假肢系統的輸入，α11，θA，θB和β1為假肢系統的響應.為方便步態分析，式(13)可以改寫為

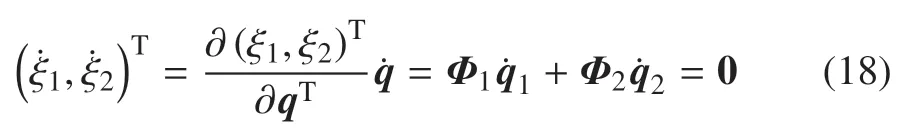
將式(18)對時間t求導可得

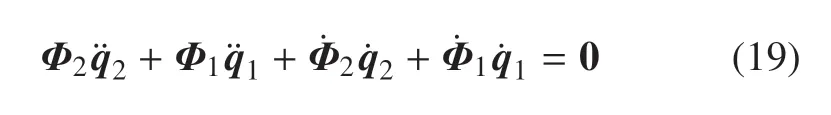
代入式(17)可得

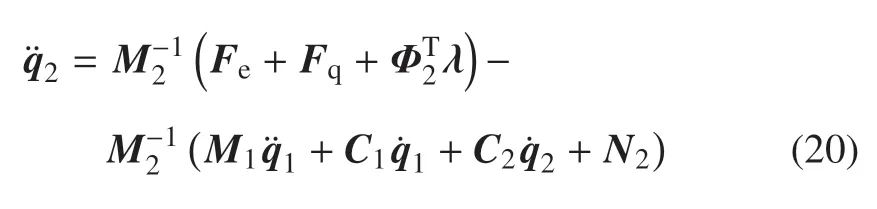
進一步，將式(20)代入式(19)可解得

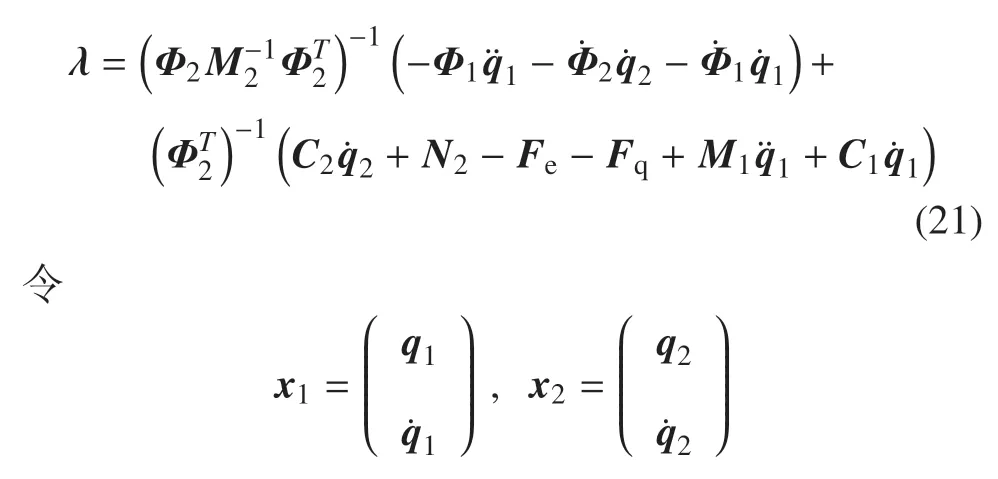
式(17)可以改寫為如下狀態方程形式

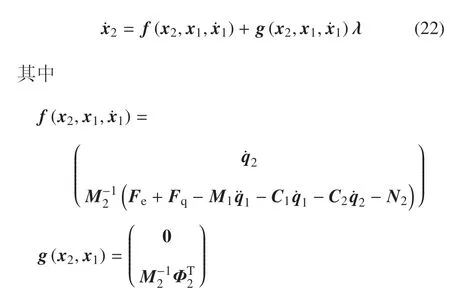
至此，我們得到了考慮四連桿約束、足--地交互力和膝關節單邊接觸力的四連桿膝關節被動假肢的動力學模型.如前所述，被動假肢是由髖關節運動驅動的，髖關節運動信號q1=(x,y,α1)T及其速度和加速度為式(22)的輸入.后續，在基于該模型的動力學分析中，q1為健康被試的實測運動信號.

2 健康被試的步態測試

該人體步態測試實驗已獲得北京大學倫理委員會批準.實驗目的在于：第一，獲得式(22)右端所需要的輸入q1，，用于四連桿膝關節被動假肢的動力學仿真；第二，將健康被試的步態信號作為健肢步態信號，與動力學仿真所得假肢步態進行比較，用于假肢運動與健肢運動的步態分析.

實驗所用設備為Cosmos Gaitway 跑臺和Vicon光學運動捕捉系統及配套分析系統.其中，Cosmos Gaitway 跑臺用于實現勻速步行環境，Vicon 光學運動捕捉系統用于捕捉人體靶點運動信號，并換算為各關節角度信息.參考步態分析軟件OrthoTrak 用戶指南中的Helen-Hayes 模型，健康被試身共貼有18 個靶點，分別為右肩靶點(R.shoulder)、左肩靶點(L.shoulder)、補償靶點(offset)、左髂前上棘靶點(R.asis)、右髂前上棘靶點(L.asis)、骶骨靶點(V.sacral)、右大腿靶點(R.thigh)、左大腿靶點(L.thigh)、右膝靶點(R.knee)、左膝靶點(L.knee)、右小腿靶點(R.shank)、左小腿靶點(L.shank)、右腳跟靶點(R.heel)、左腳跟靶點(L.heel)、右腳踝靶點(R.ankle)、左腳踝靶點(L.ankle)、右腳尖靶點(R.toe)和左腳尖靶點(L.toe).步態測試實景如圖6 所示，圖中Y軸沿著被試行走正前方，X軸沿著被試行走側向，Z軸沿著豎直向上方向.實驗過程中，健康被試(男性，身高182 cm，體重92 kg)在Cosmos Gaitway 跑臺上行走(坡度0，速度1 m/s)，Vicon 光學運動捕捉系統采樣頻率為100 Hz，采樣時長180 s.

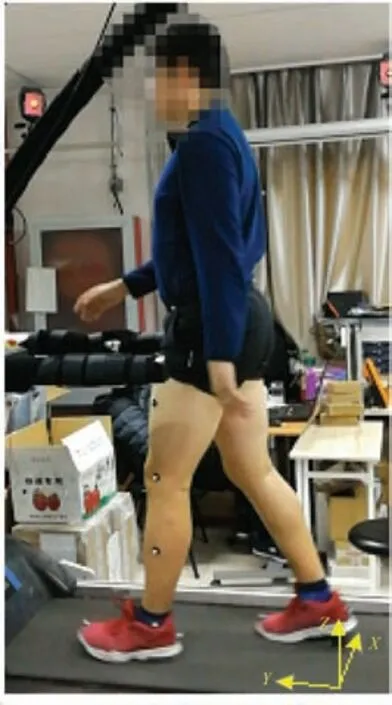
圖6 健康被試步態測試過程Fig.6 Able-bodied subject test process

實驗最終得到的數據是各靶點的空間坐標，采用Helen-Hayes 模型的角度解算方法可以得到髖關節處的空間坐標和髖、膝、踝關節的空間轉角[33].式(22)所示動力學模型為平面模型，根據坐標對應關系，本文取圖6 中髖關節處的Y軸坐標和Z軸坐標分別作為廣義坐標q中x，y坐標，取各關節繞X軸方向的轉角作為廣義坐標q中的α1，α11，β1坐標.

為使實驗數據反映健康人步態的普遍規律，本文以兩次腳跟著地(heel strike，HS)之間的時間間隔作為一個步態周期T，選取實驗數據中的30 個周期進行平均，同時將時間歸一化.處理后得到的q1數據如圖7 所示.圖7(a)中的藍色實線表示平均后的q1時程，陰影部分的上下界分別表示30 個周期中各個時刻點的最大值和最小值.從陰影部分的面積可以看出，各周期步態較為一致，實驗結果較為可靠，因此取30 個周期進行平均是合理的，能夠準確地反映q1廣義坐標的運動特征.圖7(b)中展示了廣義坐標y和α1的頻譜圖(廣義坐標x的運動不具有周期性，因此無需進行頻譜分析).可以看到，y信號中2 Hz 頻率成分的振幅較大，這是因為健康被試在一個步態周期中，左腿和右腿各走了一步，導致髖關節在豎直方向呈現兩次近似相同的起伏；α1信號中1 Hz頻率成分的振幅較大，這一點并不難理解.上述分析可以說明輸入信號q1的激勵頻率為1 Hz，這為第3 中對系統響應的分析奠定基礎.

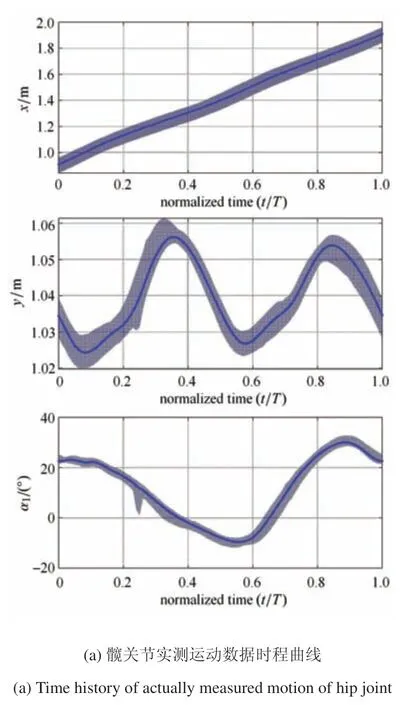
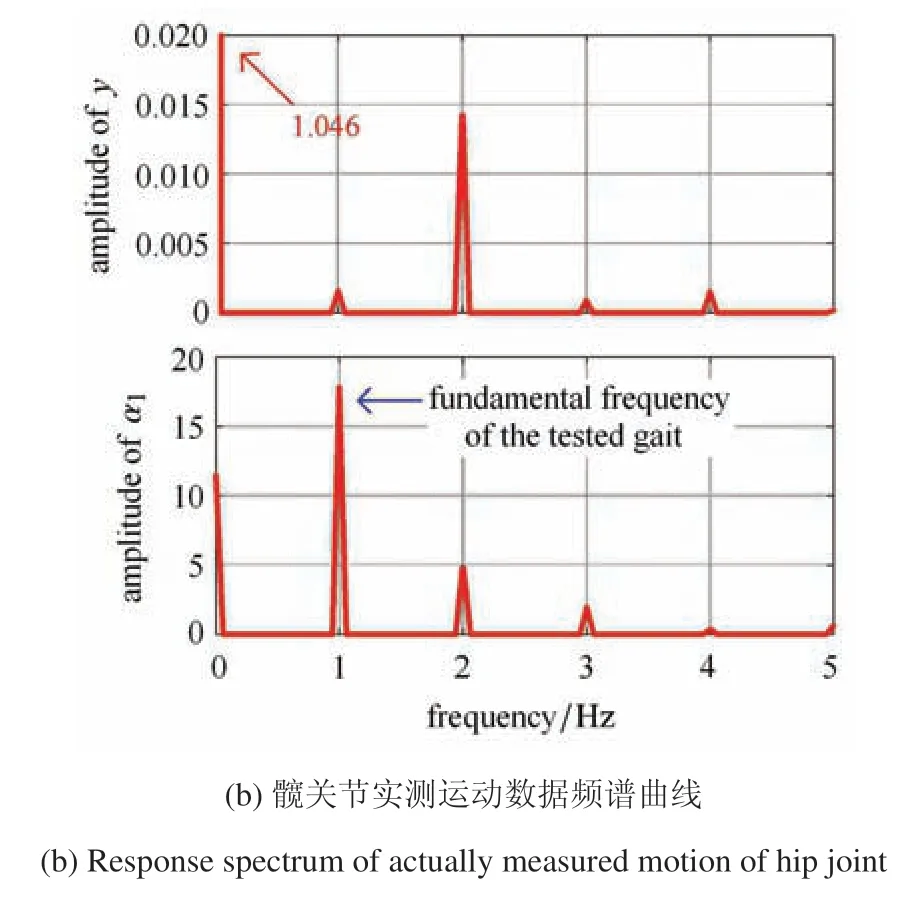
圖7 髖關節實測運動數據時程和頻譜曲線Fig.7 Time history and response spectrum of actually measured motion of hip joint

3 四連桿被動假肢的步態分析

基于式(22)并以第2 節的實驗數據作為輸入，對四連桿膝關節假肢進行動力學仿真，仿真所采用的物理參數如表2 所示.足--地交互作用力和膝關節單邊接觸力的模型參數如下

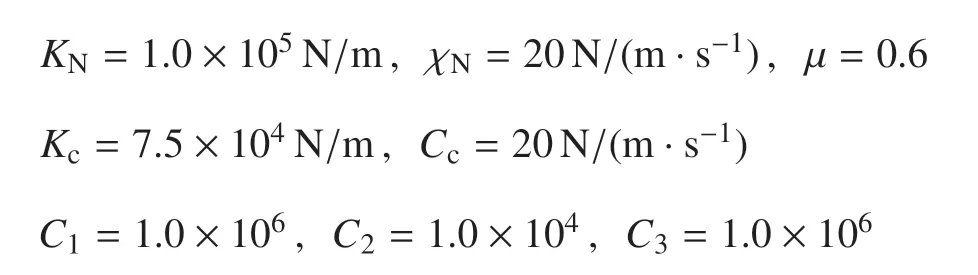
為保證仿真所得數據為假肢的穩態響應，仿真時長設置為20 個步態周期，取末5 個步態周期用于分析.

表2 仿真中的部分物理參數值Table 2 Physical parameters in numerical simulation

3.1 亞諧波頻率響應

動力學仿真中，設置液壓阻尼器阻尼/剛度比為c/k=0.05，剛度系數分別為k=1.4 × 104N/m和k=1.52×104N/m.圖8(a)展示了健康被測的實測步態數據及基于動力學模型的仿真數據，其中縱坐標定義為=α1?α11.則從圖8(a)陰影部分可以看出，當k=1.4×104N/m 時，四連桿膝關節被動假肢的動力學仿真響應的周期為2T；當k=1.52×104N/m，動力學仿真響應的周期為3T.

圖8 亞諧波響應時程曲線與頻譜曲線Fig.8 Time history and response spectrum of subharmonic response

進一步地，我們對動力學響應信號進行FFT頻譜分析.圖8(b)展示了對應于兩個時間歷程的頻譜圖.圖8(b)表明，當k=1.4 × 104N/m 時，主要的頻率成分為1 Hz 和2 Hz，同時出現了1/2 Hz 頻率成分，這一亞諧頻率成分使得響應的周期為2T；當k=1.52×104N/m 時，主要頻率成分仍為1 Hz 和2 Hz，同時出現了1/3 Hz 頻率成分，這一亞諧頻率成分使得響應的周期為3T.這些亞諧波頻率成分出現的原因在于，足--地交互作用力和膝關節單邊接觸力含有強非線性因素，可以誘發四連桿被動假肢的亞諧波響應這一強非線性動力學行為.1/2 或1/3 亞諧波響應表明，此時假肢的步態周期為健肢步態周期的2 倍或3 倍，破壞了行走時雙腿步態的協調性，本文將這種亞諧波響應稱為步態周期失諧.

通過進一步的非線性動力學分析，我們發現，通過調整激勵參數(如初始條件、相位、幅值等)，系統的穩態響應可以切換回單周期狀態.反映到式(22)所示的四連桿膝關節被動假肢模型中，即表現為髖關節運動信號的調整.例如，圖9(a)和圖9(b)分別展示了將髖關節豎向運動信號y放大為原信號1.006 倍后假肢膝關節角度的時程曲線和頻譜曲線.從圖9(a)可以看出，在增大髖關節豎向運動幅值后，假肢響應在兩個剛度值下均達到單周期穩態，周期和實測數據相同為T，并與實測數據有較好的步態一致性.圖9(b)表明，假肢的亞諧波頻率成分消失，其基頻與健肢的基頻相同，為1 Hz，步態周期不再失諧.

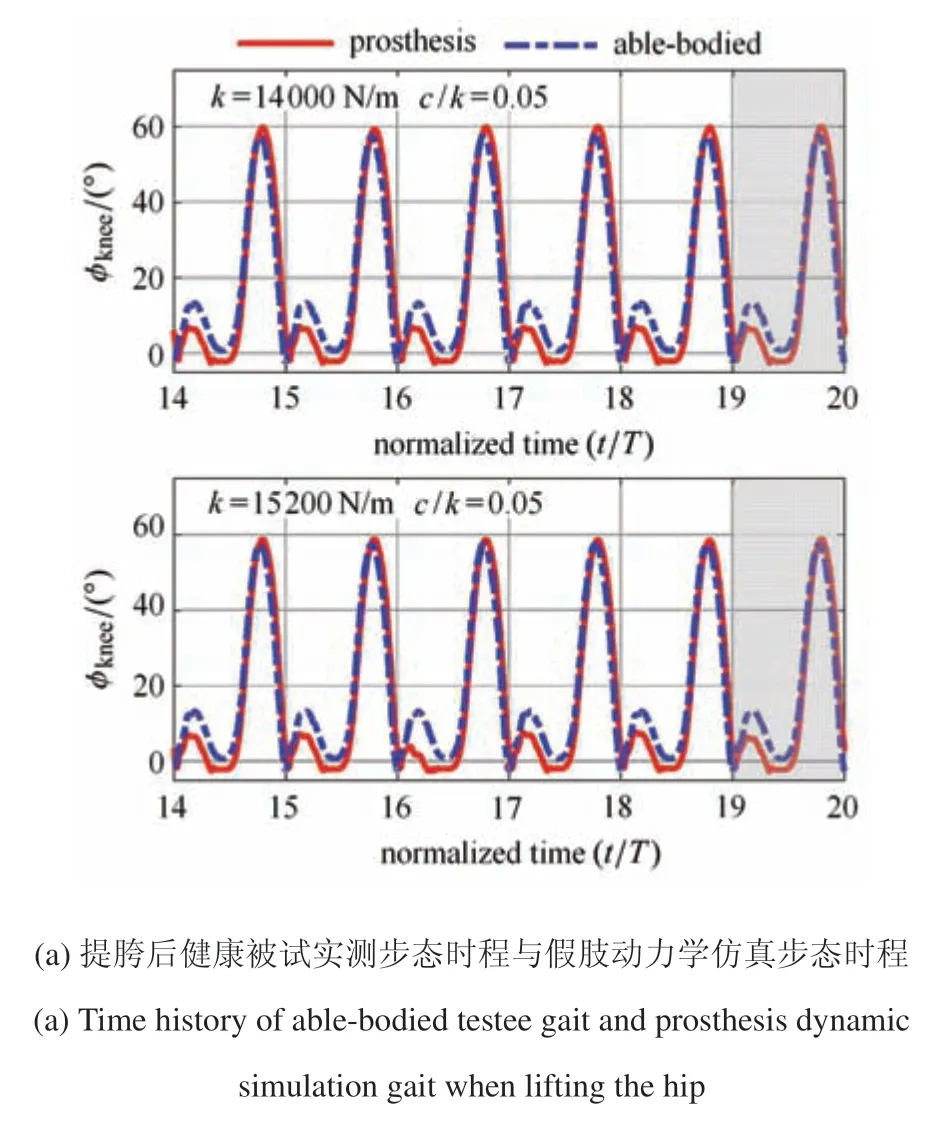
圖9 提胯后響應時程曲線與頻譜曲線Fig.9 Time history and response spectrum when lifting the hip

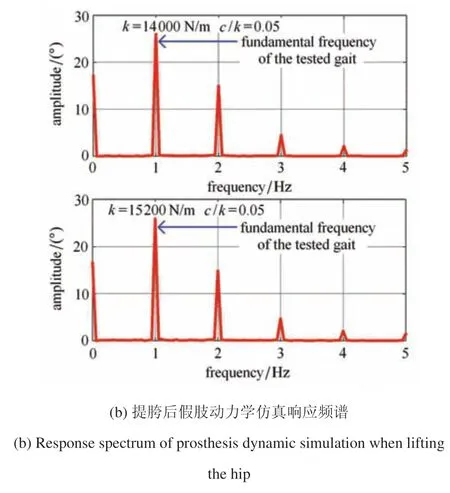
圖9 提胯后響應時程曲線與頻譜曲線(續)Fig.9 Time history and response spectrum when lifting the hip(continued)

放大髖關節豎向運動信號所反映的生物意義類似于提胯，即殘疾人在運動過程中提高胯部動作幅度的行為.圖9 呈現的結論說明，提胯動作將改善假肢步態周期的協調性，使步態不再失諧，這在定性上解釋了殘疾人穿戴假肢行走時會出現提胯等代償動作產生的原因.

注意到，在式(22)所示的四連桿膝關節被動假肢動力學模型中，四連桿的幾何參數、模型所受激勵信號均是基于實驗實測所得，因而所得結果具有較高的可信度.但上述亞諧波頻率成分和亞諧波響應，尚未在四連桿膝關節的研究文獻中見到相關報道.

數值分析進一步發現，保持四連桿膝關節液壓阻尼器阻尼比值不變，在k值達到1.6×104N/m 以上時，亞諧波頻率響應基本消失，假肢膝關節的運動恢復為單周期的穩態解，因此將k=1.6×104N/m 稱為此時的臨界k值.圖10 展示了k=1.6×104N/m 時假肢動力學仿真時程和響應頻譜，顯見假肢響應達到了單周期穩態，且周期與實測數據相同.

圖10 單周期穩態下假肢動力學仿真步態時程和響應頻譜Fig.10 Time history and response spectrum of prosthesis dynamic simulation gait under uniperiodic steady state

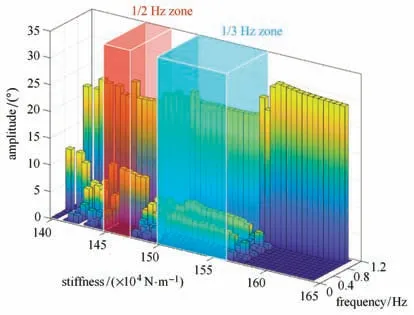
圖11 不同剛度值下假肢膝關節頻率響應圖Fig.11 Response spectrum of prosthesis knee under different values of stiffness

圖11 給出了c/k=0.05 時各個剛度值下膝關節的時程響應的頻譜圖.可以看到，在剛度值在(1.4～1.65)×104N/m 變化的過程中，響應在紅色區域(1.45～1.47)×104N/m 出現了持續且顯著的1/2 亞諧波頻率成分，在(1.47～1.5)×104N/m 進入多亞諧波頻率成分混雜的階段，在藍色區域(1.5～1.56)×104N/m 出現了持續且顯著的1/3 亞諧波頻率成分，隨后各亞諧波頻率成分逐漸減少并進入單一穩態階段(1.56～1.65)×104N/m.另外值得注意的是，在(1.4～1.45)×104N/m 階段，響應在(1.4～1.42)×104N/m 時出現了1/2 亞諧波頻率成分，而在(1.42～1.45)×104N/m 時出現多亞諧波頻率成分混雜的情況，這一部分值得在之后的研究中進一步探討.根據以上分析，可以認為在剛度值增大到一定程度時，亞諧波頻率成分會消失，將亞諧波頻率成分完全消失時的k值叫作臨界k值，并在表3 中給出了其他c/k值下的臨界k值.

分析表3 可以發現，阻尼比值越大，單周期穩態解對應的臨界k值越低.這表明，可以通過適當調大四連桿膝關節液壓阻尼器的阻尼、剛度系數來改善假肢步態周期的協調性.

表3 臨界k 值Table 3 Critical value of k

3.2 假肢膝關節最大屈曲角度

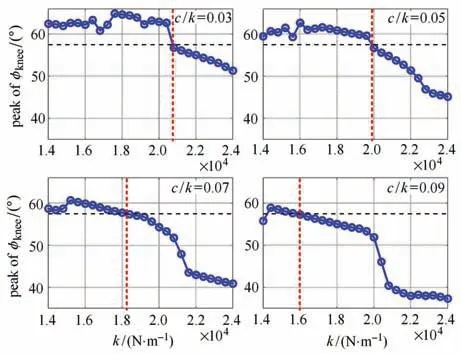
圖12 不同阻尼比值下膝關節最大屈曲角Fig.12 Peak of knee angle under different damping ratios

可以看出，隨著k值增大，膝關節最大屈曲角度呈現遞減趨勢.同時可以看出，隨著阻尼比值的增大，假肢膝關節最大屈曲角與實測膝關節最大屈曲角相等時所對應的剛度值k(紅色豎直虛線所對應的k值)也呈現遞減規律.這表明，若調大膝關節液壓阻尼器的阻尼、剛度系數，盡管假肢步態周期的協調性能夠得到改善，但假肢膝關節的最大屈曲角卻有可能偏離最優值.因此，未來的工作中，我們有必要選擇或定義合理的步態協調性指標，以便對四連桿膝關節假肢進行優化.

3.3 假肢與健肢膝關節步態一致性

為了定量衡量假肢與健肢步態的一致性，本文定義假肢與健肢膝關節信號的相關系數(correlation coefficient)，計算公式如下

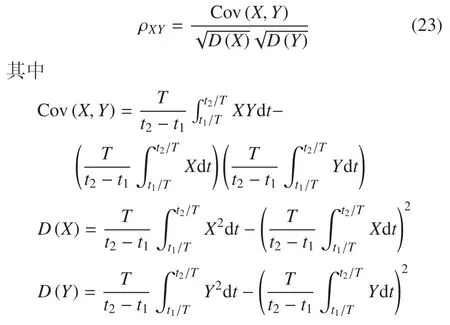
式中X=α1?α11為動力學仿真所得膝關節角度信號，Y為健康被試實測膝關節角度信號，Cov(X,Y)為X和Y信號的協方差，D(X)和D(Y)分別為X和Y信號的方差，t1/T和t2/T分別為15 和20.理論上，，ρXY越大，表示假肢膝關節角度信號與健肢膝關節角度信號一致性越高.當且僅當X≡Y時，ρXY=1.

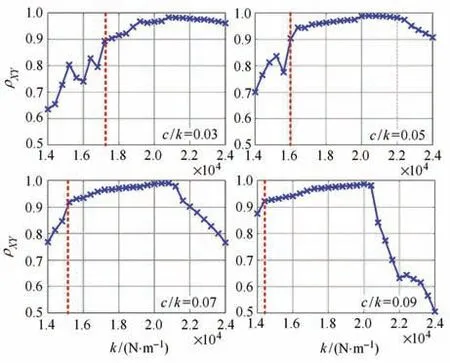
圖13 不同阻尼比值下假肢-健肢膝關節相關系數Fig.13 Prosthesis-intact knee joint correlation coefficient under different damping ratios

圖13 展示了不同的c/k值下ρXY隨液壓阻尼器剛度的變化.可以看出，在c/k較小(c/k=0.03,0.05)且k較小時，ρXY呈現抖動的狀態，這是因為，此時假肢的響應出現亞諧波頻率成分，導致ρXY出現極小值點，呈現抖動的狀態.根據3.1 節的分析可知，k在超過一定值時，假肢響應會轉變為單周期穩態響應，圖13 中已根據表3 標出臨界k值(紅色豎直虛線所對應的k值).在達到臨界k值后，ρXY呈現先增大后減小的規律性變化.這進一步驗證了3.1 節所述臨界k值的合理性.

在轉變為單周期穩態響應之后，在不同的c/k下，隨著k增大，ρXY均呈現先增大后減小的規律，因此ρXY存在一個最大值點.這表明我們可以通過四連桿膝關節液壓阻尼器阻尼、剛度參數的設計，對假肢的步態一致性進行優化.表4 反映了不同液壓阻尼器阻尼比值設置下，最大相關系數ρXY及其對應的液壓阻尼器剛度值.可以看出，在不同的液壓阻尼器阻尼比值下，最大相關系數的值均相近，且最大可得到0.989 6，這為設計液壓阻尼器的剛度和阻尼值提供了一定的理論依據.

表4 最大相關系數及對應液壓阻尼器剛度Table 4 Max ρ and its corresponding hydraulic damper stiffness

同時可以發現，隨著c/k增大，ρXY在達到最大值后的下降速度增大.因此可以發現，c/k越小，ρXY越能在一個較大的k范圍內保持平緩的變化.這表明，為了使假肢與健肢在較大的k值范圍內達到較好的步態一致性，c/k不宜取得過大.

以上分析表明，為了實現最好的步態一致性，可以通過單目標優化方法找到最合適的k值和c值.另外，也可以圍繞著步態一致性探究一些多目標優化問題，如為了實現在較大的k值范圍內達到較好的步態一致性，通過多目標優化方法找到最合適的c/k值.關于這部分的研究工作可以在后續展開.

4 結論

本文以一款四連桿膝關節假肢為研究對象，考慮足--地交互作用力和膝關節單邊接觸力等強非線性因素，采用光滑化的Kelvin-Voigt 接觸模型和庫倫摩擦模型描述足--地接觸力和摩擦力，采用光滑化的Kelvin-Voigt 接觸模型描述膝關節單邊接觸力，并基于第一類拉格朗日方程對四連桿膝關節被動假肢進行動力學建模，得到了考慮足--地交互作用力和膝關節單邊接觸力的一體化假肢動力學模型.本文將假肢動力學仿真結果與健康被試實測結果對比，系統分析了假肢動力學響應與四連桿膝關節液壓阻尼器的剛度、阻尼參數與假肢動力學響應和步態評價指標之間的關系.通過本文的研究，主要結論如下：

(1)考慮足--地交互作用力、單邊接觸力等強非線性因素后，假肢的動力學響應呈現出豐富的非線性現象，如出現了1/2 和1/3 亞諧波頻率，這種現象破壞了行走時雙腿步態的協調性.在髖關節運動中加入提胯動作后，假肢的動力學響應中的亞諧波頻率成分消失，轉變為單周期穩態響應，這為殘疾人行走時提胯等代償行為的提供了一種新的力學解釋.

(2)假肢膝關節液壓阻尼器剛度k和阻尼c對膝關節最大屈曲角度有影響.通過減小剛度k和阻尼c可以增大膝關節最大屈曲角，這有利于增大足部離地間隙，進而提高運動安全性，但過低的剛度有可能導致步態失諧，從另一方面降低運動安全性.

(3)數值計算結果表明，通過調整膝關節液壓阻尼器剛度k和阻尼c，可以使得假肢-健肢步態相關系數達到0.9 以上，這表明膝關節液壓阻尼器剛度k和阻尼c是提高假肢--健肢步態一致性的關鍵參數，為四連桿膝關節被動假肢的進一步優化提供了理論支撐.

本文的研究從動力學角度出發，對現有膝關節假肢設計技術進行了補充和完善，為基于動力學的假肢設計提供了依據.后續工作中，我們將以最大屈曲角、步態一致性等為指標，深入研究假肢動力學性能的多目標優化.

附錄A

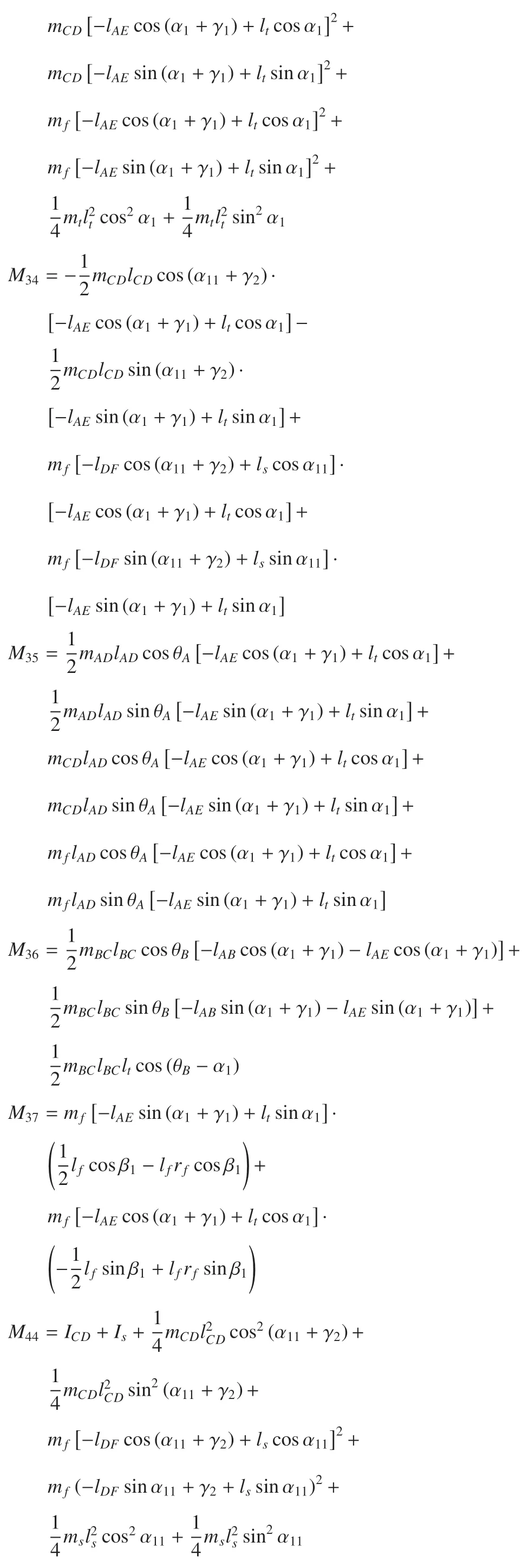
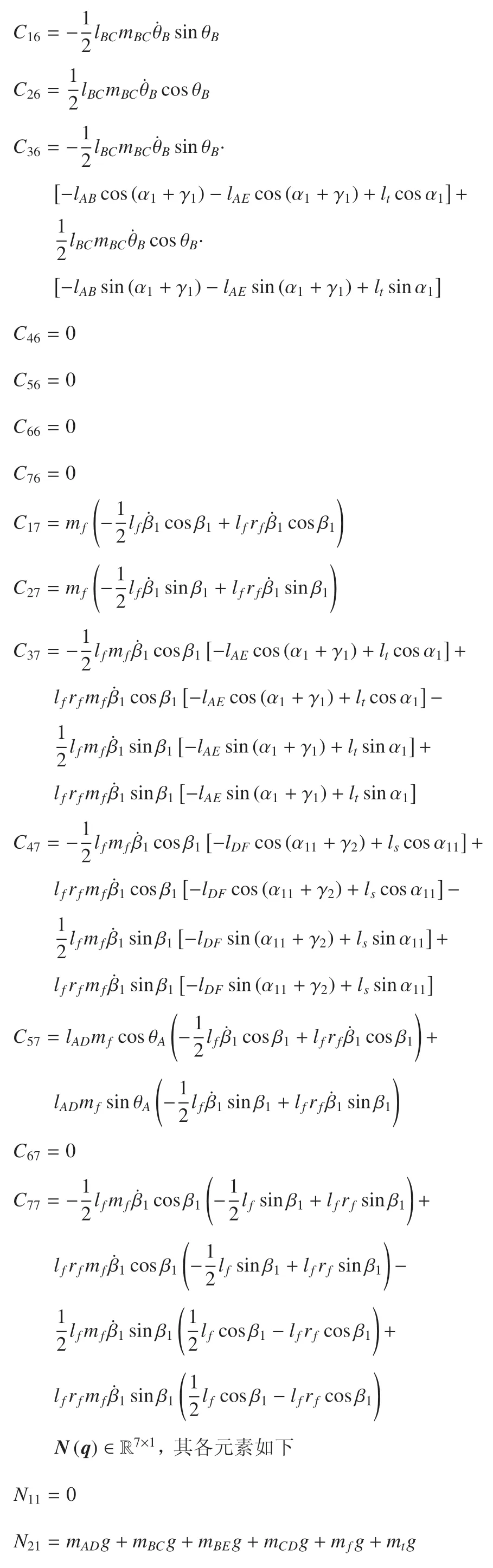
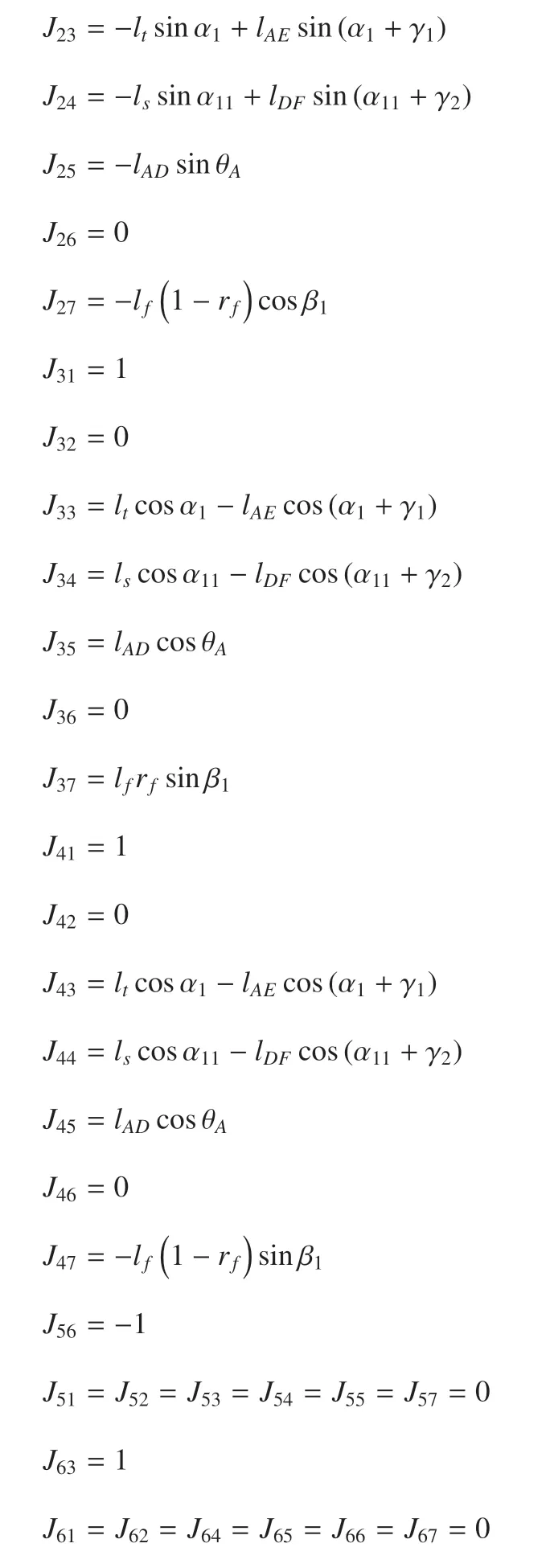
致謝本研究的第2 節實驗工作由北京大學高思源協助完成，特此感謝.