孔隙率各向異性下飽和多孔彈性地基動(dòng)力響應(yīng)1)
熊春寶 胡倩倩 郭 穎
(天津大學(xué)建筑工程學(xué)院,天津 300072)
引言
溫度、滲流及應(yīng)力場(chǎng)等多場(chǎng)耦合問(wèn)題在地?zé)豳Y源開(kāi)發(fā)、核廢料處理以及垃圾填埋等工程領(lǐng)域中十分常見(jiàn),學(xué)者們針對(duì)多孔介質(zhì)熱?水?力耦合作用理論開(kāi)展了一系列研究.Biot[1]將多孔介質(zhì)視為線彈性體,提出了耦合熱彈性理論以消除經(jīng)典熱彈理論中彈性變化對(duì)溫度沒(méi)有影響的悖論;Lord 和Shulman[2]發(fā)現(xiàn)Biot 理論中因熱傳導(dǎo)方程擴(kuò)散而使得熱傳播速度無(wú)限大的錯(cuò)誤,通過(guò)修正熱傳導(dǎo)模型建立了Lord-Shulman 廣義熱彈性理論;Noorishad 等[3]首次推導(dǎo)了飽和土體的溫度?應(yīng)力?滲流耦合基本方程,打開(kāi)了飽和土體熱?水?力三場(chǎng)耦合模型研究的新方向.國(guó)內(nèi),白冰[4-5]建立了飽和多孔介質(zhì)熱?水?力完全耦合模型的基本控制方程,分析了熱源作用下多孔飽和介質(zhì)的動(dòng)力響應(yīng)問(wèn)題及循環(huán)溫度載荷的影響;Liu等[6-7]利用Laplace 變換及反變換,分析了一維多孔彈性圓柱以及空腔球殼的熱流固耦合問(wèn)題;熊春寶等[8-10]引入正則模態(tài)法對(duì)飽和多孔彈性地基熱?水?力耦合模型進(jìn)行求解并分析參數(shù)變化對(duì)相應(yīng)物理量的影響;劉干斌等[11]推導(dǎo)了飽和多孔介質(zhì)熱流固耦合效應(yīng)下的熱彈性波動(dòng)控制方程;陳迪等[12-13]通過(guò)建立考慮熱滲效應(yīng)和熱流固耦合效應(yīng)的飽和土體固結(jié)方程,研究了圓柱熱固結(jié)問(wèn)題;劉碩等[14]提出一種新的近場(chǎng)動(dòng)力學(xué)與有限元法的耦合方法求解材料的熱傳導(dǎo)問(wèn)題;朱強(qiáng)華等[15]提出一種基于特征正交分解和有限元法的瞬態(tài)非線性熱傳導(dǎo)問(wèn)題的模型分析方法等.
以上這些研究基本都是將土體視為各向同性介質(zhì),忽略了其本身的各向異性特征.實(shí)際上,自然界中絕大多數(shù)土體是天然形成的,在產(chǎn)生的過(guò)程中由于沉積作用會(huì)呈現(xiàn)出各向異性的特征[16].國(guó)外,Rajapakse 和Wang[17-18]給出了二維均質(zhì)半無(wú)限大地基在橫觀各向同性和正交各向異性基礎(chǔ)上受簡(jiǎn)諧載荷作用的位移、應(yīng)力響應(yīng);Abousleiman 和Ekbote[19]以及Kanj 和Abousleiman[20]給出了橫觀各向同性材料熱力學(xué)問(wèn)題的一般控制方程,分析了中空?qǐng)A柱的熱力學(xué)特性;Ai 等[21-23]利用不同的積分變換方法研究了各向異性彈性體的熱彈動(dòng)力響應(yīng)和平面應(yīng)變問(wèn)題;Beskou 等[24-25]采用傅里葉級(jí)數(shù)展開(kāi)法分析了半無(wú)限大各向同性彈性地基上橫觀各向異性板受到移動(dòng)載荷作用時(shí)的動(dòng)力響應(yīng)問(wèn)題.國(guó)內(nèi),艾智勇等[26-27]推導(dǎo)了層狀橫觀各向同性地基平面變形問(wèn)題的解;韓澤軍等[28]提出了一種新的算法,用于求解橫觀各向同性層狀地基在時(shí)間簡(jiǎn)諧載荷作用下任意點(diǎn)的應(yīng)力響應(yīng);張春麗等[29-30]基于薄板理論建立了直角坐標(biāo)系正交各向異性彈性地基上覆無(wú)限大彈性板的路基路面三維空間力學(xué)模型,推導(dǎo)了板和地基在移動(dòng)載荷作用下穩(wěn)態(tài)響應(yīng)的微分方程;鄭保敬等[31]提出一種模型降階方法分析非均質(zhì)材料結(jié)構(gòu)在復(fù)雜載荷作用下的動(dòng)態(tài)響應(yīng)等.還有一些學(xué)者研究了特殊的各向異性參數(shù)對(duì)土體熱?水?力耦合作用的影響,比如Wang 等[32]研究了熱傳導(dǎo)系數(shù)各向異性參數(shù)以及滲透系數(shù)各向異性參數(shù)變化對(duì)介質(zhì)的影響;夏建中等[33]考慮滲透系數(shù)各向異性提出了在熱源作用下的二維熱固結(jié)模型;Ai 和Cang[34]研究了滲透系數(shù)各向異性參數(shù)變化對(duì)二維多層地基非軸對(duì)稱(chēng)固結(jié)的影響等.還有一些學(xué)者將孔隙率看做各向同性物理量來(lái)考慮孔隙率的影響,比如王立安等[35]基于Biot波動(dòng)理論,建立了孔隙率、密度、剪切模量和滲透系數(shù)相互耦合的非均勻飽和半空間模型;李騰風(fēng)等[36]考慮了孔隙率變化對(duì)熱源作用下非飽和土體水熱耦合作用影響等.針對(duì)孔隙率各向異性的研究較為少見(jiàn),戴婷等[37]基于功能梯度圓板中細(xì)觀孔隙依賴于各自組分變化得到整體孔隙計(jì)算式,在考慮溫度影響下建立了材料濕熱模型等.
本文在飽和多孔彈性地基基礎(chǔ)上引入孔隙率各向異性參數(shù),并結(jié)合Lord-Shulman 廣義熱彈性理論,建立了考慮孔隙率各向異性的熱?水?力耦合動(dòng)力響應(yīng)模型并推導(dǎo)其基本控制方程,采用正則模態(tài)法對(duì)控制方程進(jìn)行求解,得到了各物理量的解析表達(dá),研究了孔隙率各向異性參數(shù)變化對(duì)飽和多孔彈性地基的影響.此外,還將控制方程進(jìn)行退化驗(yàn)證模型的合理性.
1 控制方程
1.1 基本假設(shè)
本文將孔隙率各向異性參數(shù)引入飽和多孔彈性地基模型中,研究孔隙率各向異性參數(shù)變化對(duì)飽和多孔彈性地基熱?水?力耦合作用下的動(dòng)力響應(yīng)問(wèn)題的影響,基本假設(shè)如下:
(1)飽和多孔地基為流固耦合兩相介質(zhì),內(nèi)部固體顆粒不可壓縮,同時(shí)不考慮溶質(zhì)的影響;
(2)假設(shè)地基為二維半無(wú)限大彈性體,介質(zhì)變形為小變形;
(3)孔隙水滲流服從達(dá)西定律;
(4)滿足Lord-Shulman 廣義熱彈性理論;
(5)固液兩相處于熱平衡狀態(tài);
(6)假設(shè)地基孔隙率處于各向異性狀態(tài),假定豎直方向孔隙率為固定參數(shù),水平方向孔隙率由各向異性參數(shù)控制.
1.2 問(wèn)題模型
在地基上表面分別受到溫度載荷和機(jī)械載荷作用,孔隙率各向異性飽和多孔彈性地基熱?水?力耦合問(wèn)題的計(jì)算模型示意圖如圖1 所示.
1.3 基本控制方程
幾何方程
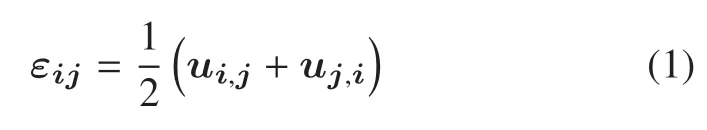
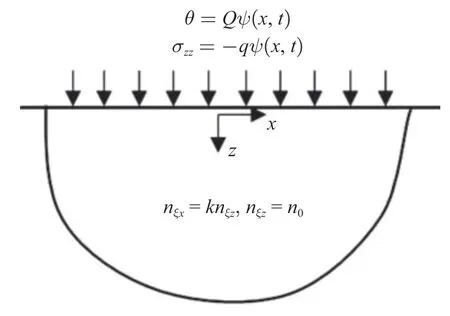
圖1 計(jì)算模型示意圖Fig.1 Schematic diagram of calculation model
式中,εij表示應(yīng)變張量,ui表示位移張量,“,” 表示對(duì)于坐標(biāo)求導(dǎo).
本構(gòu)方程
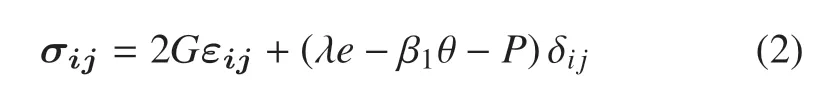
式中,σij表示應(yīng)力張量,λ,G表示拉梅常數(shù),e表示體積應(yīng)變,θ 表示溫度變化,θ=T?T0,T表示絕對(duì)溫度,T0表示初始溫度,δij表示Kronecker 符號(hào),β1表示體積應(yīng)變,β1=(3λ+2G)αs,αs表示土顆粒線性熱膨脹系數(shù),P表示超孔隙水壓力.
運(yùn)動(dòng)方程
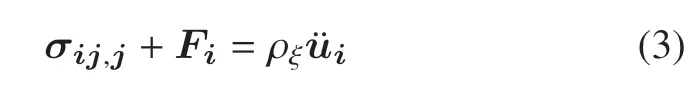
式中,Fi表示體力張量,ρξ表示不同方向的密度,表示孔隙水密度,ρs表示土顆粒密度,字母上方“.”表示對(duì)于時(shí)間t的求導(dǎo).
熱傳導(dǎo)方程
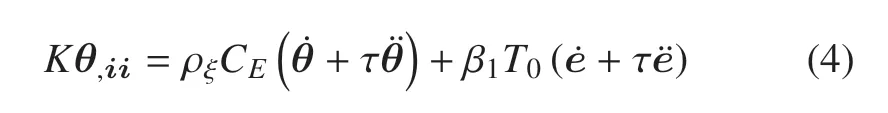
式中,K表示熱傳導(dǎo)系數(shù),CE表示單位質(zhì)量介質(zhì)的比熱容,τ 表示弛豫時(shí)間.
不計(jì)體力的運(yùn)動(dòng)平衡方程
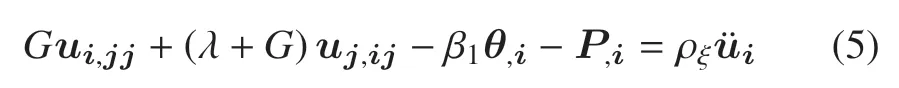
能量方程
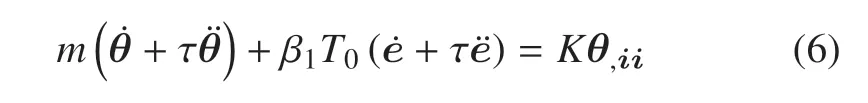
式中,m表示介質(zhì)比熱容,cw表示孔隙水比熱容,cs表示土顆粒比熱容,.
結(jié)合達(dá)西定律的流體平衡方程
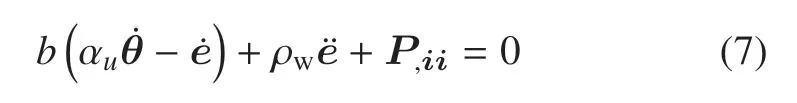
式中,αu表示介質(zhì)線膨脹系數(shù),αw表示孔隙水線性熱膨脹系數(shù),αs表示土顆粒線性熱膨脹系數(shù),其中,表示介質(zhì)的滲透系數(shù),g表示重力加速度,b=ρwg/kd.
基于二維半無(wú)限大彈性地基假設(shè),同時(shí)為使后續(xù)公式推導(dǎo)過(guò)程更為簡(jiǎn)化,引入笛卡爾坐標(biāo)系(x,y,z),將位移分量表示為ui=(u,0,w).
為使計(jì)算結(jié)果具有一定的普適性,引入下列無(wú)量綱量,該組無(wú)量綱量同參考文獻(xiàn)[38]
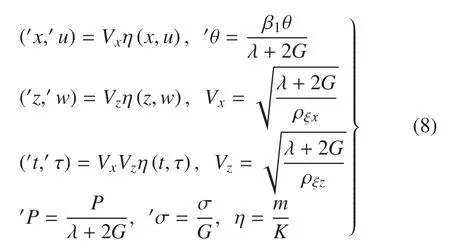
根據(jù)方程(8),方程(1)~(7)可簡(jiǎn)化為(為書(shū)寫(xiě)簡(jiǎn)便,省略點(diǎn)號(hào))
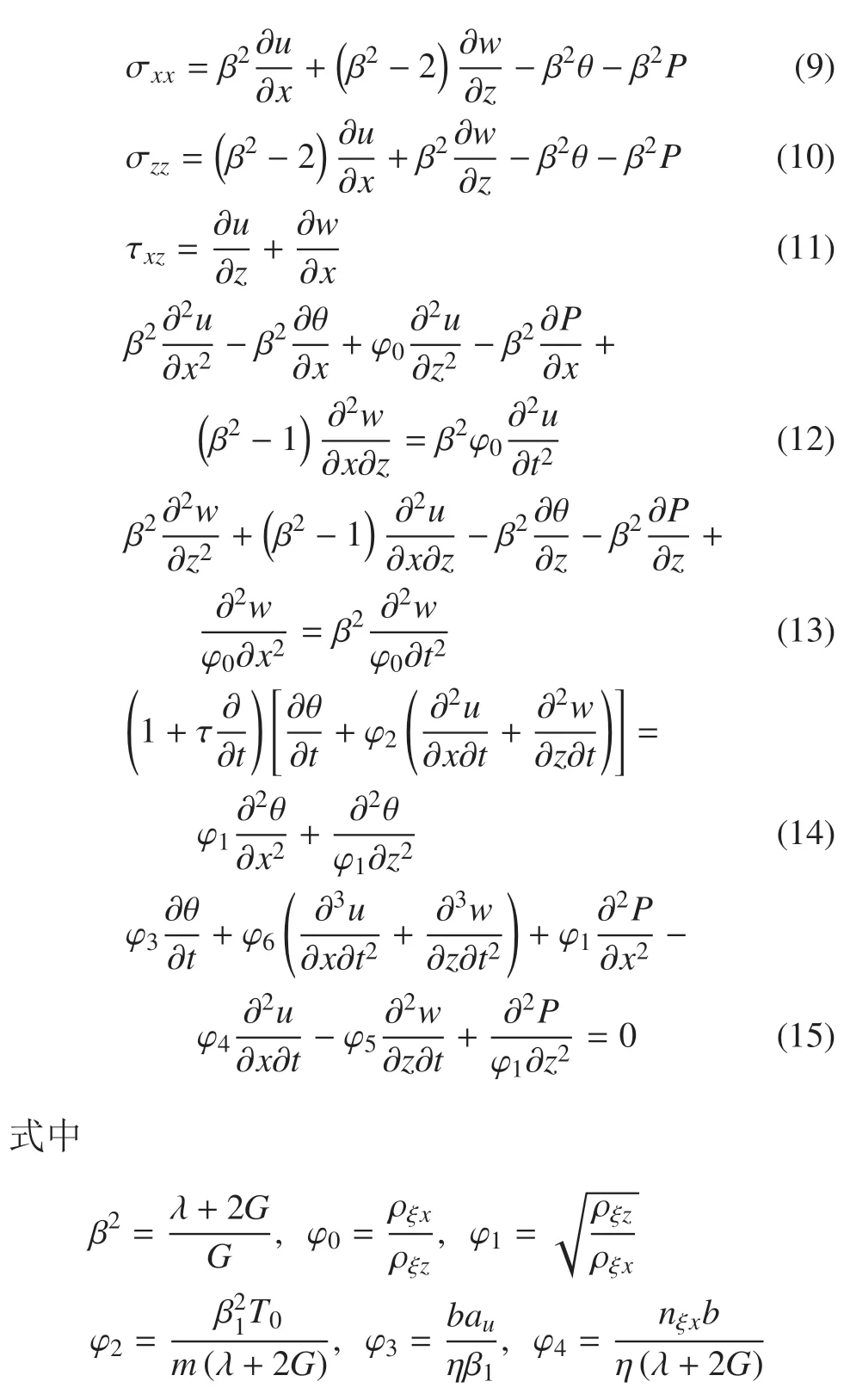
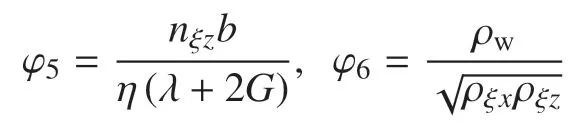
1.4 邊界條件
本文討論地基上表面受到溫度載荷、機(jī)械載荷作用時(shí)的熱?水?力耦合動(dòng)力響應(yīng)問(wèn)題,其中邊界條件如下.
(1)地基上表面受溫度載荷作用
①地基上表面應(yīng)力自由
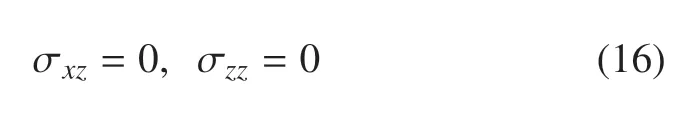
②地基上表面受到溫度載荷作用
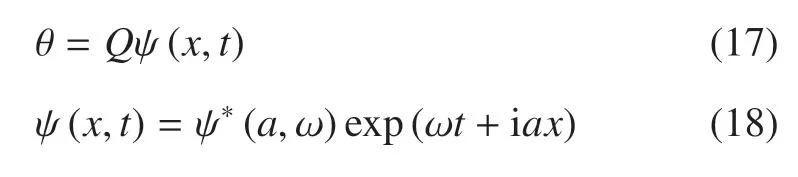
式中,Q表示溫度載荷,ω 表示頻率(復(fù)時(shí)間常數(shù)),a表示x軸方向的波數(shù),ψ(a,ω)表示載荷振幅,i 為虛數(shù)單位,i=.
③地基上表面可透水

(2)地基上表面受機(jī)械載荷作用
①地基上表面受機(jī)械載荷作用

式中,q表示機(jī)械載荷.
②地基上表面不考慮溫度載荷

③地基上表面可透水

2 二維熱?水?力耦合問(wèn)題的正則模態(tài)分析
所考慮的物理量的解均可以按照以下正則模態(tài)的形式進(jìn)行分解
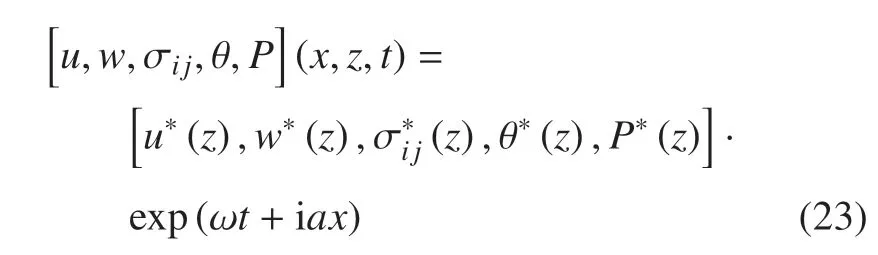
式中,u(z),w(z),,θ(z),和P(z)分別表示所考慮的物理場(chǎng)的振幅.
對(duì)方程(9)~(15)進(jìn)行正則模態(tài)分解可得如下方程

令?=?/?z,對(duì)分解后的方程進(jìn)行簡(jiǎn)化整理
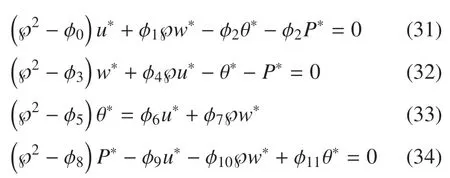
消去w(z),θ(z)和P(z),可以得到一個(gè)關(guān)于u(z)的8 階偏微分方程
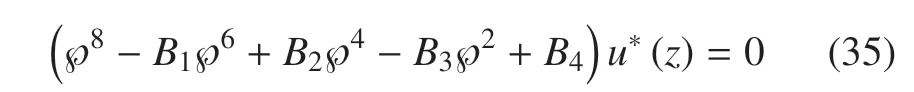
將方程(35)因式分解后可得
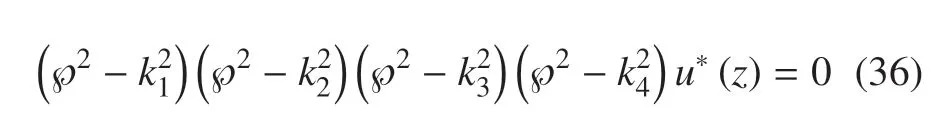
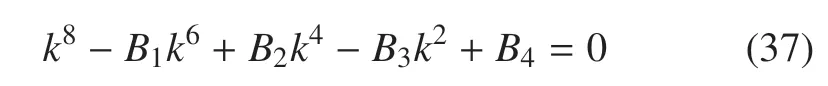
其中
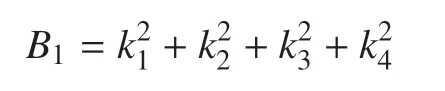
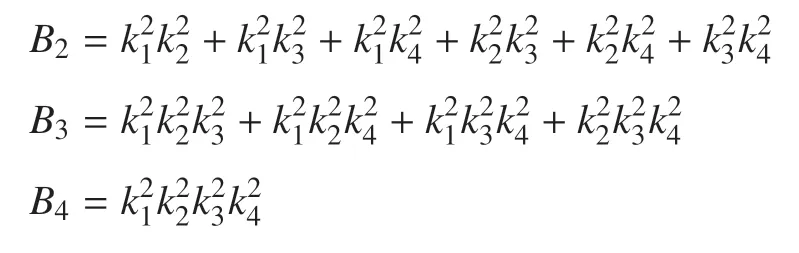
方程的解可表示為如下形式
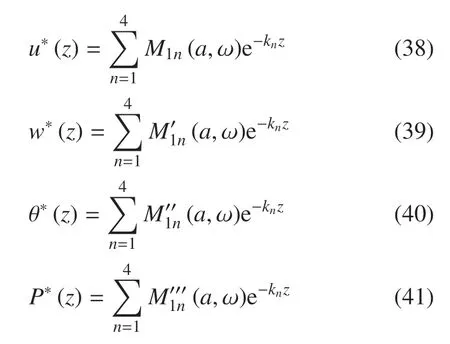
其中
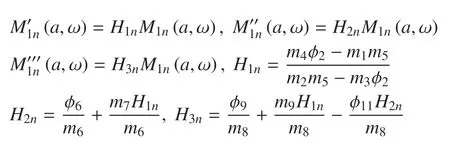
代入應(yīng)力分量表達(dá)式中得

3 算例分析及結(jié)果討論
以飽和多孔半無(wú)限大彈性地基為例,分別在地基的上表面施加溫度載荷和機(jī)械載荷,研究孔隙率各向異性參數(shù)變化對(duì)地基深度增加方向和波的傳播方向上豎向位移、超孔隙水壓力、豎向應(yīng)力及溫度的影響.根據(jù)求得的解析解表達(dá)式,利用Maple 軟件,結(jié)合邊界條件得到了各物理的分布規(guī)律圖.
3.1 計(jì)算模型驗(yàn)證
本文是考慮孔隙率各向異性參數(shù)的影響而建立的控制方程,當(dāng)孔隙率各向異性參數(shù)k=1.0 時(shí)方程可退化為各向同性耦合動(dòng)力響應(yīng)方程,其結(jié)果可與參考文獻(xiàn)[38]進(jìn)行對(duì)比,從而驗(yàn)證模型的合理性.
研究中所需要的基本參數(shù)取值同參考文獻(xiàn)[38]一致,ψ=1,a=1.2.其他參數(shù)詳見(jiàn)表1.

表1 飽和多孔彈性地基熱?水?力多物理場(chǎng)耦合基本參數(shù)Table 1 Basic parameters of themo-hydro-mechanical coupling of saturated porous elastic foundation
3.2 地基深度增加方向各物理量變化規(guī)律
在地基上表面分別施加溫度載荷和機(jī)械載荷作用,研究地基深度增加方向上孔隙率各向異性參數(shù)變化對(duì)各物理量的影響.以下8 幅圖為x=1.0 平面上t=0.5 時(shí)各物理量的變化規(guī)律圖.其中,退化模型曲線與參考文獻(xiàn)結(jié)果曲線吻合較好,進(jìn)而驗(yàn)證了模型的合理性.
圖2~圖5 為溫度載荷下豎向位移、超孔隙水壓力、豎向應(yīng)力和溫度變化規(guī)律圖,整體來(lái)說(shuō),孔隙率各向異性參數(shù)變化對(duì)豎向位移和溫度影響較小,對(duì)超孔隙水壓力和豎向應(yīng)力影響較大.豎向位移變化趨勢(shì)都是由壓縮狀態(tài)逐漸轉(zhuǎn)為膨脹最后趨于平緩衰減至零;溫度則是逐漸衰減至零.超孔隙水壓力曲線和豎向應(yīng)力曲線峰值均逐漸減小,且峰值出現(xiàn)位置向地基深度減小方向移動(dòng),超孔隙水壓力減幅為52.72%和61.06%,豎向應(yīng)力減幅為16.92%和26.13%.這主要是由于孔隙水對(duì)溫度較為敏感,隨著孔隙率各向異性參數(shù)增大,兩個(gè)方向孔隙分布更不均勻影響地基排水速率,進(jìn)而使得超孔隙水壓力變小,而超孔隙水壓力變化影響了豎向應(yīng)力的變化.
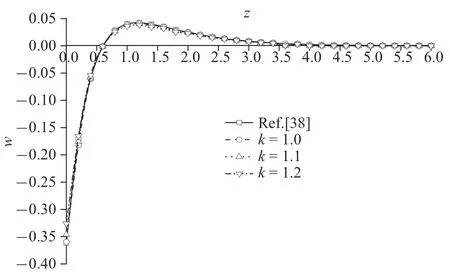
圖2 溫度載荷作用時(shí)無(wú)量綱豎向位移分布規(guī)律圖Fig.2 The distribution of non-dimension vertical displacement under thermal load
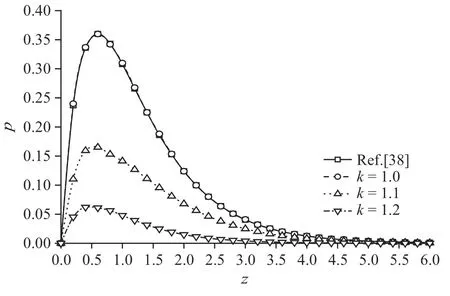
圖3 溫度載荷作用時(shí)無(wú)量綱超孔隙水壓力分布規(guī)律圖Fig.3 The distribution of non-dimension excess pore water pressure under thermal load
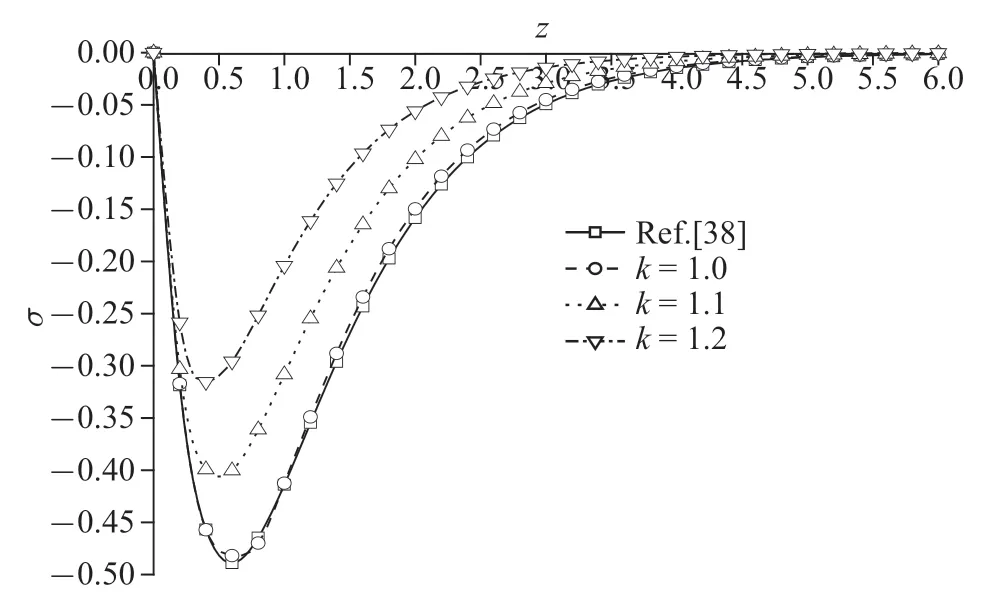
圖4 溫度載荷作用時(shí)無(wú)量綱豎向應(yīng)力分布規(guī)律圖Fig.4 The distribution of non-dimension vertical stress under thermal load
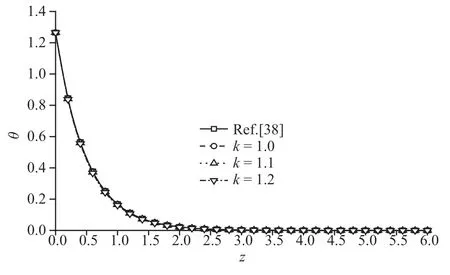
圖5 溫度載荷作用時(shí)無(wú)量綱溫度分布規(guī)律圖Fig.5 The distribution of non-dimension temperature under thermal load
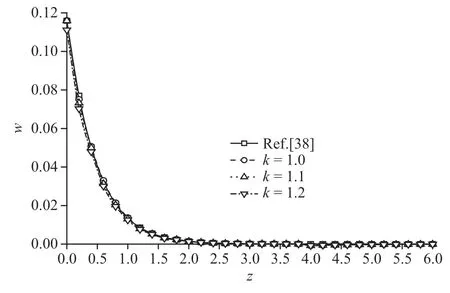
圖6 機(jī)械載荷作用時(shí)無(wú)量綱豎向位移分布規(guī)律圖Fig.6 The distribution of non-dimension vertical displacement under mechanical load
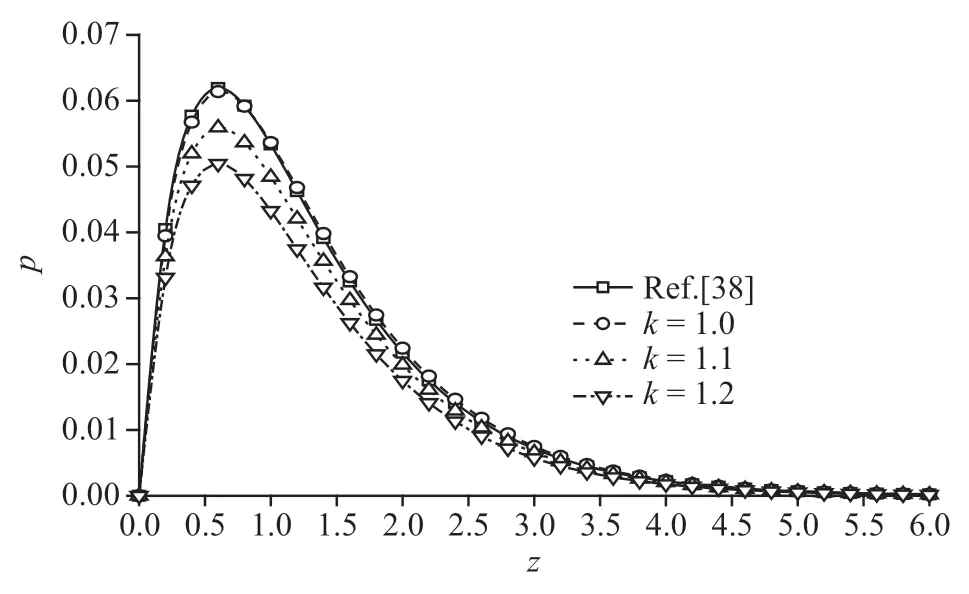
圖7 機(jī)械載荷作用時(shí)無(wú)量綱超孔隙水壓力分布規(guī)律圖Fig.7 The distribution of non-dimension excess pore water pressure under mechanical load
圖6~圖9 為機(jī)械載荷下豎向位移、超孔隙水壓力、豎向應(yīng)力和溫度變化規(guī)律圖,整體來(lái)說(shuō),孔隙率各向異性對(duì)豎向位移和豎向應(yīng)力影響較小,對(duì)超孔隙水壓力和溫度影響較大.圖6 和圖8 中,豎向位移和豎向應(yīng)力均逐漸衰減至零,但應(yīng)力衰減速率比位移衰減速率略快.圖7 超孔隙水壓力曲線隨各向異性參數(shù)的增加逐漸減小,尤其是峰值處,有較為明顯變化,峰值減幅為8.89%和9.82%;圖9 中隨著各向異性參數(shù)的增大,溫度的峰值逐漸減小,減幅依次為18.46%和19.74%.
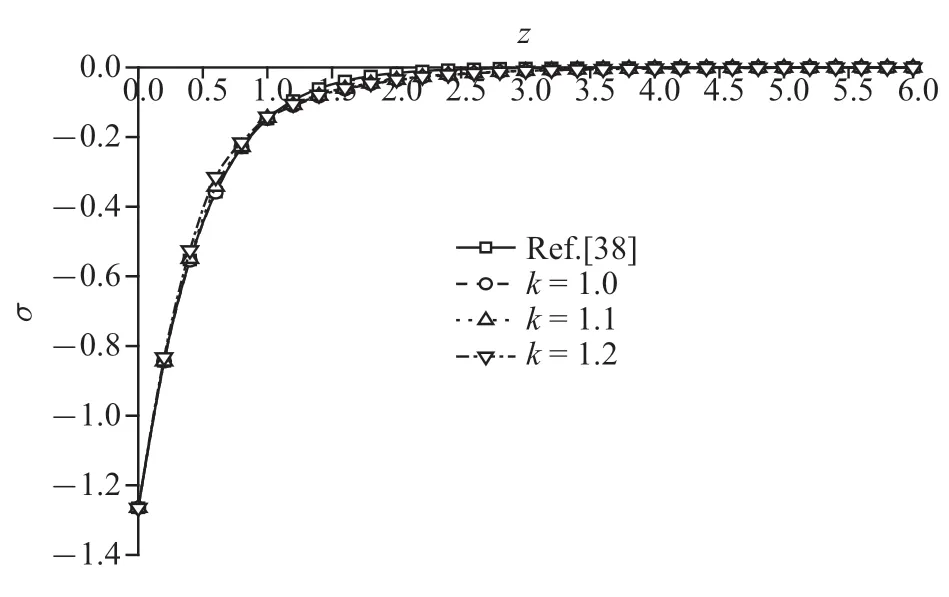
圖8 機(jī)械載荷作用時(shí)無(wú)量綱豎向應(yīng)力分布規(guī)律圖Fig.8 The distribution of non-dimension vertical stress under mechanical load
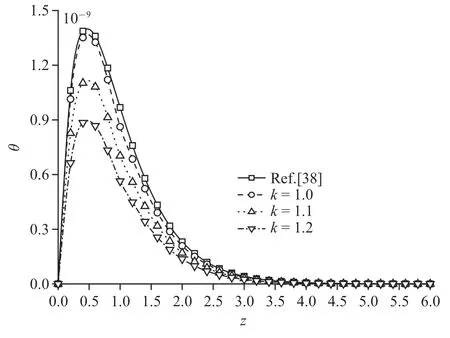
圖9 機(jī)械載荷作用時(shí)無(wú)量綱溫度分布規(guī)律圖Fig.9 The distribution of non-dimension temperature under mechanical load
從圖6~圖9 可以看出,溫度曲線量級(jí)相對(duì)較小,說(shuō)明單純的機(jī)械載荷作用產(chǎn)生的熱量不多,可忽略不計(jì).孔隙率各向異性參數(shù)變化對(duì)超孔隙水壓力和溫度的影響趨勢(shì)相同,但對(duì)溫度的影響更明顯,這是由于隨著各向異性參數(shù)增大,使得地基熱量耗散更為迅速,引起明顯的溫度變化,而孔隙率各向異性參數(shù)的變化影響了地基中孔隙的分布,參數(shù)增大,孔隙分布更為不均勻,導(dǎo)致超孔隙水壓力峰值減小.
3.3 波的傳播方向上各物理量變化規(guī)律
本節(jié)從波的傳播方向上研究了地基上表面分別施加溫度載荷和機(jī)械載荷作用時(shí)孔隙率各向異性參數(shù)變化對(duì)所考慮物理量的影響.圖10~圖17 為z=1.0 平面上t=0.5 時(shí)各物理量的變化規(guī)律圖.
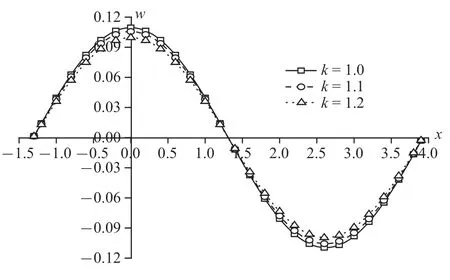
圖10 溫度載荷作用時(shí)無(wú)量綱豎向位移分布規(guī)律圖Fig.10 The distribution of non-dimension vertical displacement under thermal
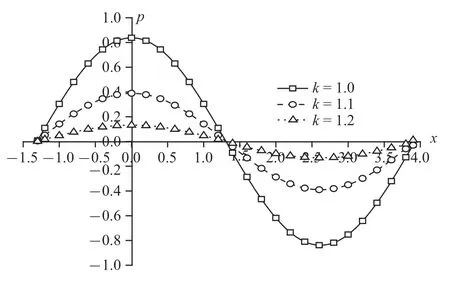
圖11 溫度載荷作用時(shí)無(wú)量綱超孔隙水壓力分布規(guī)律圖Fig.11 The distribution of non-dimension excess pore water pressure under thermal load
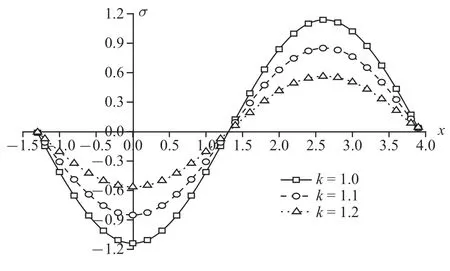
圖12 溫度載荷作用時(shí)無(wú)量綱豎向應(yīng)力分布規(guī)律圖Fig.12 The distribution of non-dimension vertical stress under thermal load
圖10~圖13 為溫度載荷下豎向位移、超孔隙水壓力、豎向應(yīng)力和溫度變化規(guī)律圖.整體來(lái)說(shuō),隨著孔隙率各向異性參數(shù)的增大,物理量峰值逐漸減小.可以明顯看出,孔隙率各向異性參數(shù)變化對(duì)超孔隙水壓力和豎向應(yīng)力的影響遠(yuǎn)超于豎向位移和溫度.其中,超孔隙水壓力減幅依次為53.50%和66.15%,豎向應(yīng)力減幅依次為25.26%和33.77%,而豎向位移減幅在4%附近,溫度減幅穩(wěn)定在2%左右.這是因?yàn)榭紫堵实淖兓绊懙娇紫端?隨著各向異性參數(shù)增大,孔隙分布更為不均勻,孔隙水排出速率受到影響,導(dǎo)致超孔隙水壓力減幅明顯,而超孔隙水壓力變化又會(huì)影響豎向應(yīng)力,使得豎向應(yīng)力變化.
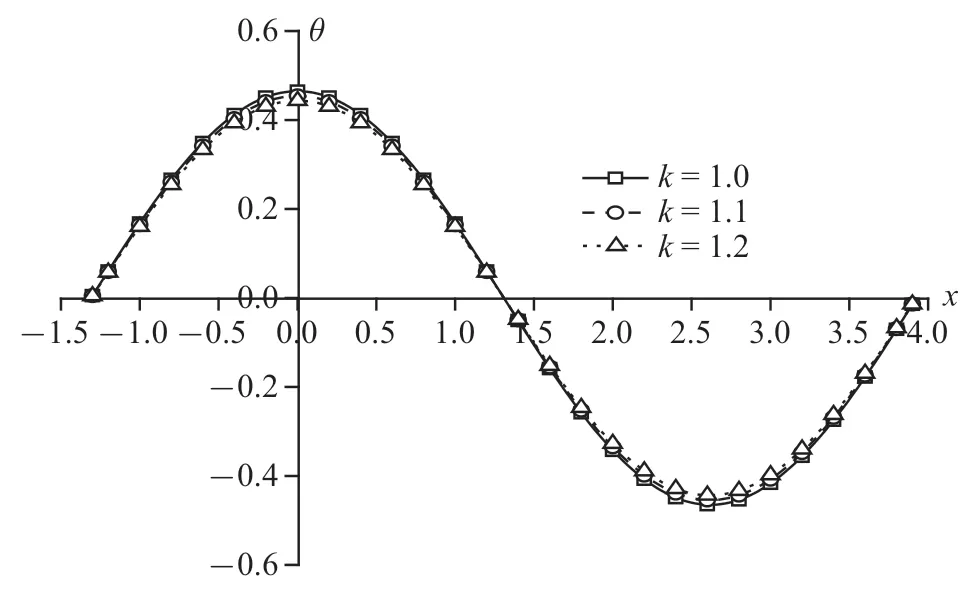
圖13 溫度載荷作用時(shí)無(wú)量綱溫度分布規(guī)律圖Fig.13 The distribution of non-dimension temperature under thermal load
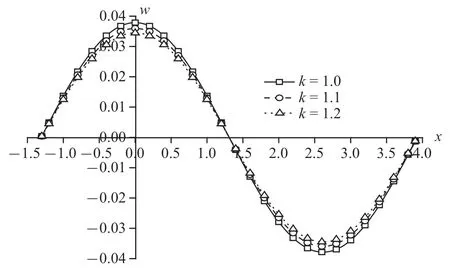
圖14 機(jī)械載荷作用時(shí)無(wú)量綱豎向位移分布規(guī)律圖Fig.14 The distribution of non-dimension vertical displacement under mechanical load
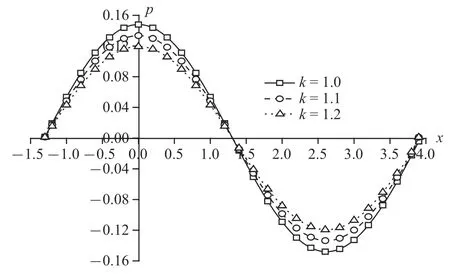
圖15 機(jī)械載荷作用時(shí)無(wú)量綱超孔隙水壓力分布規(guī)律圖Fig.15 The distribution of non-dimension excess pore water pressure under mechanical load

圖16 機(jī)械載荷作用時(shí)無(wú)量綱豎向應(yīng)力分布規(guī)律圖Fig.16 The distribution of non-dimension vertical stress under mechanical load
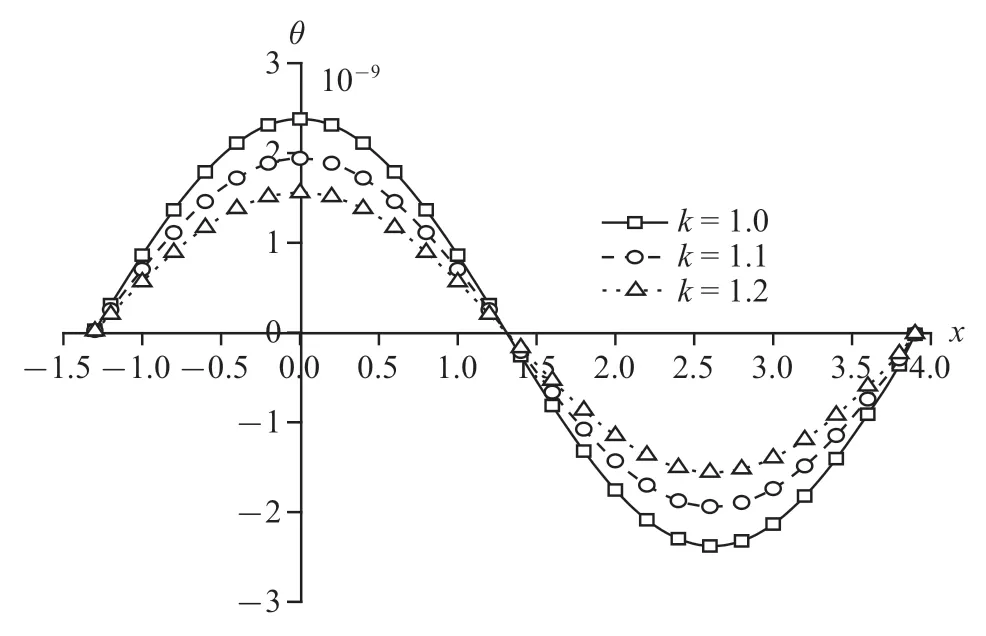
圖17 機(jī)械載荷作用時(shí)無(wú)量綱溫度分布規(guī)律圖Fig.17 The distribution of non-dimension temperature under mechanical load
圖14~圖17 為機(jī)械載荷下豎向位移、超孔隙水壓力、豎向應(yīng)力和溫度的變化規(guī)律圖.孔隙率各向異性對(duì)豎向位移和豎向應(yīng)力變化不太明顯,減幅相對(duì)較小;對(duì)超孔隙水壓力和溫度變化明顯,其中溫度減幅更大,為18.46%和19.74%.單純的機(jī)械載荷作用產(chǎn)生于地基中的溫度很小,孔隙率的變化使得地基散熱更為迅速,所以對(duì)溫度的影響更加明顯.
4 結(jié)論
本文在飽和多孔彈性地基基礎(chǔ)上引入孔隙率各向異性參數(shù),并結(jié)合Lord-Shulman 廣義熱彈性理論,建立了考慮孔隙率各向異性的熱?水?力耦合動(dòng)力響應(yīng)模型并推導(dǎo)其基本控制方程,采用正則模態(tài)法對(duì)簡(jiǎn)化方程進(jìn)行求解,得到了各物理量的解析表達(dá),分析了孔隙率各向異性參數(shù)變化對(duì)相關(guān)物理量的影響.主要結(jié)論如下:
(1)考慮孔隙率各向異性參數(shù)的飽和多孔彈性地基熱?水?力耦合動(dòng)力響應(yīng)模型可退化為各向同性飽和多孔彈性地基熱?水?力耦合動(dòng)力響應(yīng)模型,退化后物理量變化規(guī)律與參考文獻(xiàn)[38]曲線分布規(guī)律一致,驗(yàn)證了模型的合理性;
(2)地基深度增加方向上,地基上表面受溫度載荷作用時(shí),孔隙率各向異性參數(shù)變化對(duì)超孔隙水壓力和豎向應(yīng)力影響明顯,隨著各向異性參數(shù)增大,峰值逐漸減小,峰值所在位置向靠近地基上表面移動(dòng);地基上表面受機(jī)械載荷作用時(shí),孔隙率各向異性參數(shù)變化對(duì)超孔隙水壓力和溫度影響明顯,隨著各向異性參數(shù)增大,峰值逐漸減小,峰值所在位置向靠近地基上表面移動(dòng);
(3)波的傳播方向上,孔隙率各向異性參數(shù)變化對(duì)各物理量均有影響,使得峰值逐漸減小,地基上表面受溫度載荷作用時(shí),對(duì)超孔隙水壓力和豎向應(yīng)力影響明顯;地基上表面受機(jī)械載荷作用時(shí),對(duì)超孔隙水壓力和溫度影響明顯.
附 錄
εij應(yīng)變張量
σij應(yīng)力張量
e體積應(yīng)變
T絕對(duì)溫度
δijKronecker 符號(hào)
P超孔隙水壓力
ρξ不同方向的密度
ρξz豎直方向的密度
ρs土顆粒密度
nξx水平方向的孔隙率
K熱傳導(dǎo)系數(shù)
τ 熱弛豫時(shí)間
cw孔隙水比熱容
αu介質(zhì)線膨脹系數(shù)
αw孔隙水線性熱膨脹系數(shù)
g重力加速度
ω 頻率(復(fù)時(shí)間常數(shù))
ψ(a,ω) 載荷振幅
ui位移張量
λ,G拉梅常數(shù)
θ 溫度變化
T0初始溫度
β1體積應(yīng)變
Fi體力張量
ρξx水平方向的密度
ρw孔隙水密度
nξ不同方向的孔隙率
nξz豎直方向的孔隙率
CE單位質(zhì)量介質(zhì)比熱容
m介質(zhì)比熱容
cs土顆粒比熱容
kd介質(zhì)的滲透系數(shù)
αs土顆粒線性熱膨脹系數(shù)
Q溫度載荷
ax軸方向的波數(shù)
q機(jī)械載荷

