柔性鉸柔性桿機器人動力學建模、仿真和控制1)

方五益 郭 晛 黎 亮 章定國

(南京理工大學理學院,南京 210094)

引言

空間機械臂[1]是一種強耦合、高度非線性的復雜柔性多體系統(tǒng).而關(guān)節(jié)柔性和臂桿柔性的客觀存在是引起空間機械臂振動的根本原因,因此柔性鉸柔性桿機器人的研究具有實際工程意義.

對于柔性桿件的研究,Likins[2]用混合坐標法建立柔性多體動力學零次近似剛?cè)狁詈夏Ｐ?Book[3]采用假設模態(tài)法表示桿件的彈性變形,借助于齊次變換矩陣,推導出遞推形式的多桿柔性機械臂系統(tǒng)的拉格朗日動力學方程.章定國[4]在Book 的研究基礎(chǔ)上,考慮了桿件的扭轉(zhuǎn)效應,優(yōu)化了遞推過程,并給出了仿真算例.洪嘉振等[5]從連續(xù)介質(zhì)力學的基本原理出發(fā),建立了一次近似剛?cè)狁詈蟿恿W模型,并通過實驗驗證其正確性.文獻[6～9]運用一次近似剛?cè)狁詈夏Ｐ蛯θ嵝粤哼M行了相關(guān)研究.陳思佳等[10]保留一次近似耦合模型中耦合變形量的高階項,建立了更精確的高次剛?cè)狁詈蟿恿W模型.最近幾年,吳吉等[11]用絕對節(jié)點坐標法研究了帶集中質(zhì)量的旋轉(zhuǎn)柔性曲梁動力學特性.范紀華等[12]用絕對節(jié)點坐標法對柔性單擺的動力學問題進行研究.另外,范紀華等[13]對旋轉(zhuǎn)中心剛體?功能梯度材料梁剛?cè)釤狁詈蟿恿W特性進行了研究.

關(guān)于柔性關(guān)節(jié)的研究,Spong[14]將柔性關(guān)節(jié)簡化為線性扭轉(zhuǎn)彈簧模型.Bridges 等[15]考慮了摩擦、柔性非線性和運動誤差等,提出了更精確的關(guān)節(jié)模型.周勝豐等[16]用Kane 方法推導出柔性多桿多鉸機器人動力學方程,通過仿真算例說明鉸的柔性不可忽略.劉俊[17]用遞推拉格朗日方法推導出柔性多桿多鉸機器人剛?cè)狁詈蟿恿W方程,方程中還考慮了鉸的質(zhì)量效應和扭轉(zhuǎn)變形.范紀華等[18]研究了關(guān)節(jié)柔性對機器人動力學的影響.Xi 等[19]建立了由單根柔性桿和單個柔性鉸組成的全柔機器人的動力學模型,且研究了柔性桿與柔性鉸之間的耦合關(guān)系.邊樞宇[20]基于Kane 法建立了多桿全柔機器人的動力學方程,并通過單桿全柔機器人的仿真算例說明桿柔性與關(guān)節(jié)柔性對機器人動力學響應的影響.Al-Bedoor 等[21]建立了末端帶有載荷的單桿全柔機器人的動力學模型.Zhang 等[22]建立了多個柔性桿和柔性鉸并存的空間全柔機器人的動力學模型,模型中考慮了柔性桿件的彎曲、扭轉(zhuǎn)和拉伸變形.Qian 等[23]詳細推導了空間全柔機器人的動力學模型,并開發(fā)了多桿機械臂的通用軟件包.陳思佳等[24]推導了帶桿端集中質(zhì)量的柔性單桿單鉸機器人高次剛?cè)狁詈蟿恿W方程,并進行了仿真分析.

為保證復雜系統(tǒng)的動力學方程得以高效高精度的求解,諸多學者們對于柔性多體系統(tǒng)動力學的數(shù)值積分方法也進行了相關(guān)研究.如芮筱亭等[25]對柔性多體系統(tǒng)動力學建模理論和數(shù)值求解方法都進行了研究.郭晛等[26]對柔性多體系統(tǒng)動力學的數(shù)值積分方法進行了研究.

對于空間機械臂動力學控制的研究,與逆動力學求解息息相關(guān).Guaraci[27]詳細介紹并討論了欠驅(qū)動機械臂前饋控制的逆動力學方法.Krzysztf[28]提出了一種基于逆動力學的柔性鉸機器人的非線性反饋控制方法.Jankowski[29]使用柔性鉸機器人動力學模型,提出了一種基于逆動力學的離散控制方法.

以上關(guān)于柔性鉸機器人的研究,暫未考慮鉸阻尼的存在.在太空中,空間機械臂發(fā)生振動后,需要很長時間才能恢復到穩(wěn)定的狀態(tài).此時鉸阻尼的存在可使系統(tǒng)快速穩(wěn)定下來,因此鉸阻尼的研究具有工程意義.本文采用遞推拉格朗日方法,推導出考慮鉸阻尼的柔性機器人剛?cè)狁詈蟿恿W方程,研究鉸的柔性對機器人動力學響應和動力學控制的影響,以期為柔性機器人的減振與控制提供參考.

1 柔性鉸柔性桿機器人的動力學建模

1.1 柔性鉸柔性桿機器人的物理模型

柔性鉸柔性桿機器人是由n個鉸和n根桿件組成的空間鏈式多體系統(tǒng),如圖1 所示.

圖1 柔性鉸柔性桿機器人Fig.1 The robot with flexible joints and flexible links

柔性桿模型基于Euler-Bernoulli 梁,變形處于線彈性階段.模型中考慮了桿件拉壓、彎曲變形和扭轉(zhuǎn)變形.柔性鉸模型基于Spong 的柔性關(guān)節(jié)簡化模型,將柔性鉸看成線性扭轉(zhuǎn)彈簧,并考慮鉸阻尼的存在.τi為鉸i的驅(qū)動力矩,ki為鉸i扭轉(zhuǎn)剛度系數(shù),ci為鉸i阻尼系數(shù),qi1為鉸i驅(qū)動裝置的角位移,qi2為鉸i傳到桿件i的角位移.qi2?qi1為鉸柔性引起的扭轉(zhuǎn)變形.

1.2 柔性機器人的運動學描述

在建模過程中,引入齊次坐標和齊次變換矩陣來描述桿件的位置和姿態(tài).為清楚表示各坐標系之間的轉(zhuǎn)換關(guān)系,在i桿的近端和遠端各建立兩個正交坐標系:坐標系(XbYbZb)i固定在i桿的近端,沿Xb沿桿件i未變形時的中性軸;坐標系(XdYdZd)i固定在i桿的遠端,在桿i未變形時,(XdYdZd)i看作是(XbYbZb)i沿桿件i的軸線方向平移桿件i的長度Li而成;坐標系(HxHyHz)i固定在i桿件的遠端,z軸沿著關(guān)節(jié)的轉(zhuǎn)軸;坐標系固定在桿件i的近端,鉸i未動時,與(HxHyHz)i?1重合.可見,坐標系(XdYdZd)i與坐標系(HxHyHz)i之間的4×4齊次變換矩陣dHi是一個常數(shù)陣,坐標系(HxHyHz)i與(XbYbZb)i之間的變換矩陣Hbi也是一個常數(shù)陣,與(HxHyHz)i?1之間的變換矩陣只是鉸i鉸變量qi2的函數(shù).

定義鉸i的變換矩陣為Ai,即從坐標系(Xd Yd Zd)i?1到坐標系(Xb Yb Zb)i的變換矩陣,則

定義Ei是桿件i的變形變換矩陣,即從坐標系(XbYbZb)i到桿件i變形后的坐標系(XdYdZd)i的變換矩陣.由于桿件i的變形是基于小變形假設,故Ei可近似表達為

其中,xij,yij,zij分別是桿件i的第j變形線位移模態(tài)在坐標系(XbYbZb)i的三軸上的分量;θxij,θyij,θzij分別是桿件i的第j變形角位移模態(tài)在坐標系(XbYbZb)i的三軸上的分量;δij是桿件i的第j個模態(tài)坐標;Ni是桿件i的模態(tài)數(shù).

令Wi是基座坐標系(XbYbZb)0到(XbYbZb)i之間的齊次變換矩陣,則

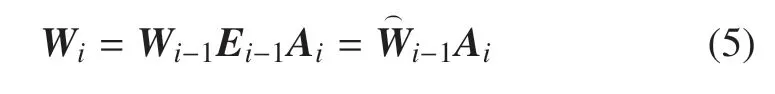
采用假設模態(tài)法描述桿件的變形,考慮由桿件橫向變形引起的縱向耦合變形.桿i上某點P(η,0,0)變形后在連體坐標系中的齊次坐標ihi為

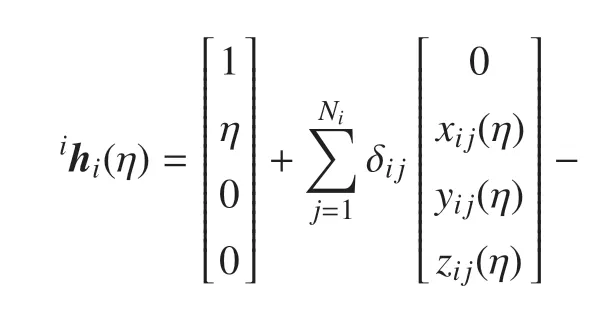
式中,xijk(η)是采用非線性應變場產(chǎn)生的高階耦合項,與傳統(tǒng)零次動力學模型不同,考慮了該項的高次剛?cè)狁詈蟿恿W模型能夠捕捉到大范圍運動與變形的相互影響,所得結(jié)果更加精確.xijk(η)可表示為

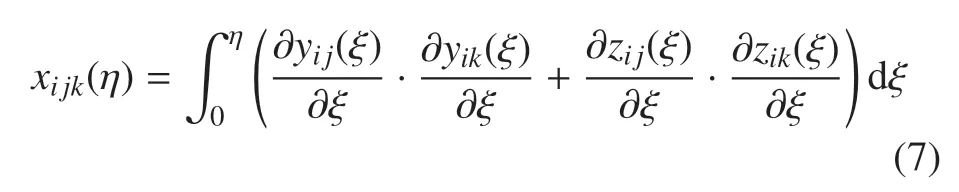
該點在基座坐標系中的齊次坐標hi可以表示為

將hi對時間求導,可以得到該點的速度為

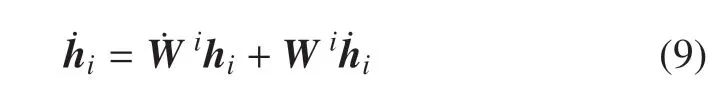
1.3 系統(tǒng)的動能和勢能

系統(tǒng)的動能包括桿的動能和鉸的動能.桿i的動能可表示為

上式中,Li為桿i長度,μi為柔性桿單位長度質(zhì)量,Tr(·)表示對括號中的矩陣求跡,Jxi為桿i繞xi軸單位長度轉(zhuǎn)動慣量,θxi為桿i繞xi軸扭轉(zhuǎn)角.式(10)中,右邊的第一項為桿件大范圍運動、縱向拉壓變形運動和橫向彎曲變形運動引起的動能,第二項為桿件扭轉(zhuǎn)變形運動引起的動能.其中,θxi可表示為

柔性鉸i的動能分為平動動能和轉(zhuǎn)動動能.對于平動動能,把鉸i看作桿i靠近鉸i端的集中質(zhì)量計入桿的動能.而柔性鉸i的轉(zhuǎn)動動能可表示為

式中,Jri為鉸i轉(zhuǎn)動慣量,φi是轉(zhuǎn)子的角位移,經(jīng)過齒輪變速后輸出角位移qi1到柔性鉸上,因此qi1=φi/ni,其中ni為齒輪傳動比.于是式(12)可表示為

綜上,系統(tǒng)的總動能為

系統(tǒng)的勢能包括柔性桿和柔性鉸的彈性變形勢能以及它們的重力勢能.柔性桿i的彈性勢能包括拉壓變形勢能、彎曲變形勢能、扭轉(zhuǎn)變形勢能

其中,Ei是桿i的楊氏模量,Gi是桿i的剪切模量,Axi是桿i的橫截面積,Ixi是桿i橫截面關(guān)于中性軸的極面積慣性矩,Iyi和Izi是桿i橫截面關(guān)于yi和zi軸的面積慣性矩,θyi和θzi為桿i繞yi和zi軸轉(zhuǎn)角.θxi如式(11)所示,θyi,θzi可表示為

xi為桿件i的拉壓變形,可表示為

柔性鉸i的彈性勢能為

系統(tǒng)的彈性勢能為

系統(tǒng)的重力勢能為

其中,g為重力加速度陣,ri為桿i質(zhì)心位置矩陣,其具體形式見參考文獻[23].于是系統(tǒng)的總勢能為

1.4 系統(tǒng)的動力學方程

取廣義坐標

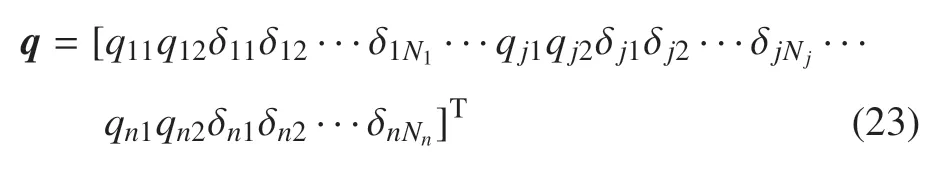
將系統(tǒng)的動能(14)和勢能(22)代入到第二類拉格朗日方程

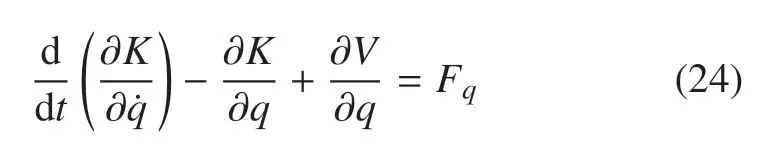
得到系統(tǒng)的動力學方程組為

以上得到的方程為考慮鉸阻尼的柔性桿柔性鉸機器人剛?cè)狁詈蟿恿W方程,其中的相關(guān)變量可以參看文獻[6-7,17,23].雙下劃線部分為考慮鉸阻尼時產(chǎn)生項,該項會使系統(tǒng)的動力學響應衰減.以上方程最終可整理成如下矩陣形式

其中,J為廣義質(zhì)量矩陣,R為廣義力矩陣.

2 柔性鉸柔性桿機器人的動力學仿真

2.1 驗證算例

使用文獻[17]中由兩個柔性桿和兩個柔性鉸組成的空間機器人模型,如圖2 所示.桿件1 與桿件2 之間的間距為d=0.475 m,由于此間距的存在,桿件1 會發(fā)生扭轉(zhuǎn)變形.考慮鉸質(zhì)量產(chǎn)生的項為=5 kg·m2.桿件1 初始角度為π/4,系統(tǒng)在重力作用下運動.取與文獻[17]中相同的模型參數(shù),如表1 所示.

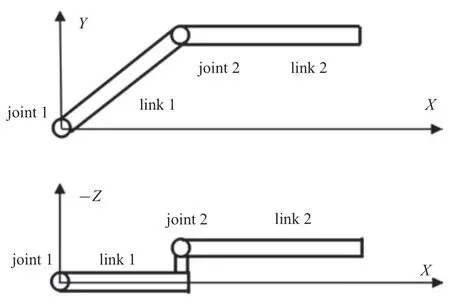
圖2 柔性二連桿機器人Fig.2 The flexible robot with two joints and two links

表1 柔性機器人桿件參數(shù)Table 1 The parameters of the flexible robot

將本文不考慮鉸阻尼時(即雙下劃線項為零時)桿1 的扭轉(zhuǎn)變形與參考文獻[17]中桿1 的扭轉(zhuǎn)變形進行對比,如圖3 所示.本文結(jié)果與文獻[17]中結(jié)果一致,驗證了本文建模和程序的正確性.

2.2 柔性單鉸單桿機器人動力學仿真

圖3 結(jié)果對比Fig.3 The comparison of results from the present model with those from Ref.[17]

圖4 柔性單鉸單桿模型Fig.4 The flexible robot with single joint and single link

柔性單鉸單桿機器人模型如圖4 所示.柔性桿長度L=1.8 m,桿密度ρ=2.766×103kg/m3,桿的橫截面積S=2.5×10?4m2,桿截面慣性矩I=1.302 1×10?10m4,桿的彈性模量E=6.9×1010N/m2,驅(qū)動轉(zhuǎn)子齒輪的傳動比ni=10,驅(qū)動轉(zhuǎn)子的轉(zhuǎn)動慣量Jr=7.0×10?3kg·m2.q1為驅(qū)動轉(zhuǎn)子傳到鉸上的角位移,q2為鉸傳到桿件的角位移.驅(qū)動力矩為τ,鉸的剛度系數(shù)為k,鉸的阻尼系數(shù)為c.由于鉸柔性的存在,鉸存在扭轉(zhuǎn)變形,驅(qū)動轉(zhuǎn)子上的驅(qū)動轉(zhuǎn)角q1并不等于桿件的實際轉(zhuǎn)角q2.

輸入的驅(qū)動力矩為

該驅(qū)動力矩的大小為一個周期的正弦函數(shù),故對于剛性鉸剛性桿機器人,在所給力矩作用下,機器人從靜止開始轉(zhuǎn)動,先加速后減速最終回到靜止狀態(tài).

2.2.1 鉸剛度對機器人動力學響應的影響

為了探究鉸剛度對柔性機器人動力學響應的影響,對不考慮鉸阻尼時不同鉸剛度的情況進行仿真分析.圖5 為不同鉸剛度時鉸的驅(qū)動轉(zhuǎn)角.圖6 為不同鉸剛度時鉸的實際轉(zhuǎn)角.圖7 為不同鉸剛度時驅(qū)動轉(zhuǎn)角與實際轉(zhuǎn)角的差值.

圖5 鉸的驅(qū)動轉(zhuǎn)角Fig.5 The driving angular displacements of the joint

圖6 鉸的實際轉(zhuǎn)角Fig.6 The actual angular displacements of the joint

圖7 驅(qū)動轉(zhuǎn)角與實際轉(zhuǎn)角的差Fig.7 The difference between the driving angles and the actuating angles

在剛性鉸情況下驅(qū)動轉(zhuǎn)角q1和實際轉(zhuǎn)角q2相等,而在柔性鉸情況下,鉸存在扭轉(zhuǎn)變形,驅(qū)動轉(zhuǎn)角q1和實際轉(zhuǎn)角q2不相等.鉸的剛度越大,驅(qū)動轉(zhuǎn)角q1和實際轉(zhuǎn)角q2越接近.隨著鉸剛度的增大,驅(qū)動轉(zhuǎn)角q1和實際轉(zhuǎn)角q2的振動幅值變小,振動頻率變大.故可調(diào)節(jié)鉸的剛度系數(shù)的大小來實現(xiàn)柔性機器人的減震和控制.

2.2.2 鉸阻尼對機器人動力學響應的影響

為了探究鉸阻尼對柔性機器人動力學響應的影響,對相同鉸剛度時不同鉸阻尼的系統(tǒng)進行仿真分析.將柔性鉸的剛度取k=50 N·m/rad.圖8 為不同鉸阻尼時鉸的驅(qū)動轉(zhuǎn)角.圖9 為不同鉸阻尼時鉸的實際轉(zhuǎn)角.圖10 為不同鉸阻尼時鉸驅(qū)動轉(zhuǎn)角與實際轉(zhuǎn)角的差值.

圖8 鉸的驅(qū)動轉(zhuǎn)角Fig.8 The driving angles of joint

圖9 鉸的實際轉(zhuǎn)角Fig.9 The actuating angles of joint

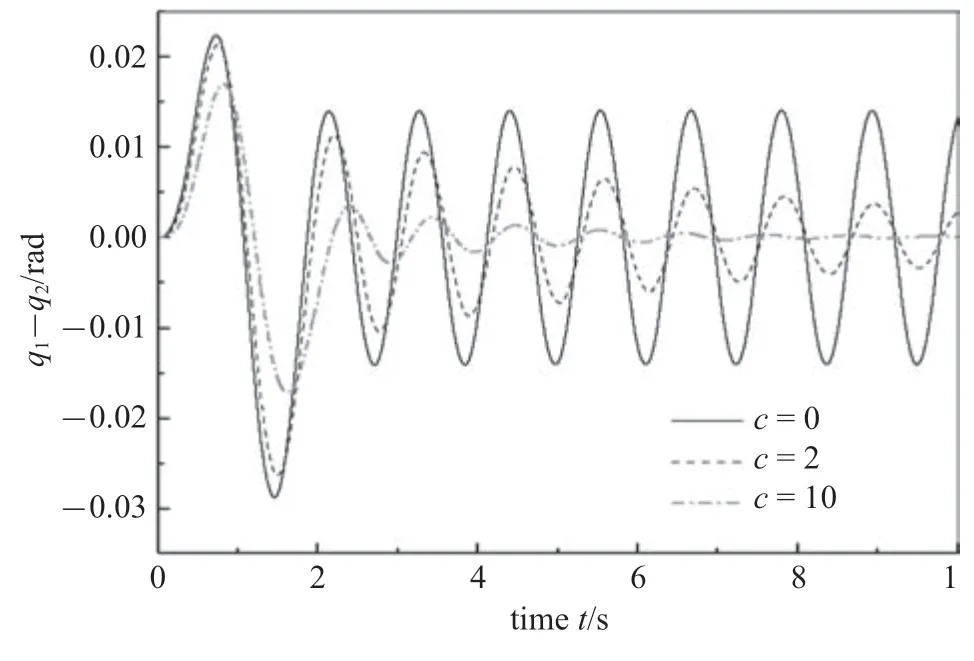
圖10 驅(qū)動轉(zhuǎn)角與實際轉(zhuǎn)角的差Fig.10 The difference between the driving angles and the actuating angles

不考慮鉸阻尼時,驅(qū)動轉(zhuǎn)角q1、實際轉(zhuǎn)角q2、會一直振動下去.鉸阻尼的存在,會使驅(qū)動轉(zhuǎn)角q1、實際轉(zhuǎn)角q2的振動衰減.且鉸阻尼越大,驅(qū)動轉(zhuǎn)角q1、實際轉(zhuǎn)角q2衰減越快.故可調(diào)節(jié)鉸阻尼系數(shù)的大小來實現(xiàn)柔性機器人的減振和控制.

3 鉸柔性對機器人動力學控制的影響

機器人控制屬于動力學逆問題,即已知系統(tǒng)軌跡對應的位移、速度和加速度求解所需關(guān)節(jié)力或力矩.在系統(tǒng)動力學方程中,廣義力可分為與控制有關(guān)的廣義力和包含了重力、離心力等與控制無關(guān)的其他部分的廣義力.其中,控制廣義力作為控制變量,對機器人運動實施跟蹤控制.這里,控制廣義力可以是作動器驅(qū)動力、阻尼力、彈簧力或者它們的線性組合.為求解此控制變量,首先需要建立系統(tǒng)無控制時的動力學方程,通過在此動力學方程中添加機器人末端運動所需要的約束方程,建立機器人系統(tǒng)帶有約束方程的動力學微分代數(shù)方程.其次,按照相關(guān)控制要求,釋放一定數(shù)量的控制變量,在此情況下求解微分代數(shù)形式的動力學方程,獲得滿足運動需求的系統(tǒng)運動參數(shù).最后由求解得到的運動參數(shù),通過逆動力學求解得到所需要的控制變量,以此控制變量為前饋輸入,再通過反饋控制方法(如PID 方法)施加到系統(tǒng)上,便可使系統(tǒng)完成指定的運動.

以圖11 所示機械臂為例,系統(tǒng)由3 根剛性桿和3 個轉(zhuǎn)動鉸組成.系統(tǒng)參數(shù)為:Li=7.11 m,ρiSi=44.287 kg/m,=5 kg·m2,i=1,2,3.使三連桿末端執(zhí)行器做如下圓周運動

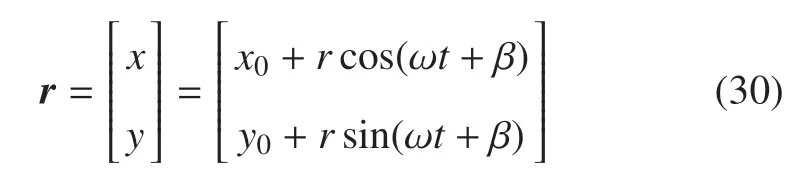
式中r=5 m,ω=0.314 rad/s,β=?π/2.

圖11 三連桿機械臂Fig.11 Three-link robot

在剛性鉸情況下,經(jīng)過逆動力學求解得到機械臂3 個鉸上所需施加的驅(qū)動力矩如圖12 所示,此剛性鉸系統(tǒng)的運動位形如圖13 所示.

圖12 關(guān)節(jié)力矩Fig.12 The joint-torques

圖13 三連桿機械臂的位形Fig.13 The configuration of the 3-link system

將圖12 中剛性鉸情況下求得的驅(qū)動力矩施加到柔性鉸系統(tǒng)時,得到柔性鉸系統(tǒng)末端執(zhí)行器的運動軌跡如圖14 所示.此時,柔性鉸的剛度取k1=k2=k3=1330 N·m/rad.

圖14 末端執(zhí)行器運動軌跡Fig.14 The movement of end-effector

由圖14 可見,桿末端軌跡為不規(guī)則運動,與指定圓周運動差別巨大.因此在機器人動力學控制時,鉸的柔性不可忽略,需要對柔性鉸系統(tǒng)進行研究.對柔性鉸系統(tǒng)進行動力學逆問題求解得到的3 個鉸上所需施加的驅(qū)動力矩如圖15 所示.

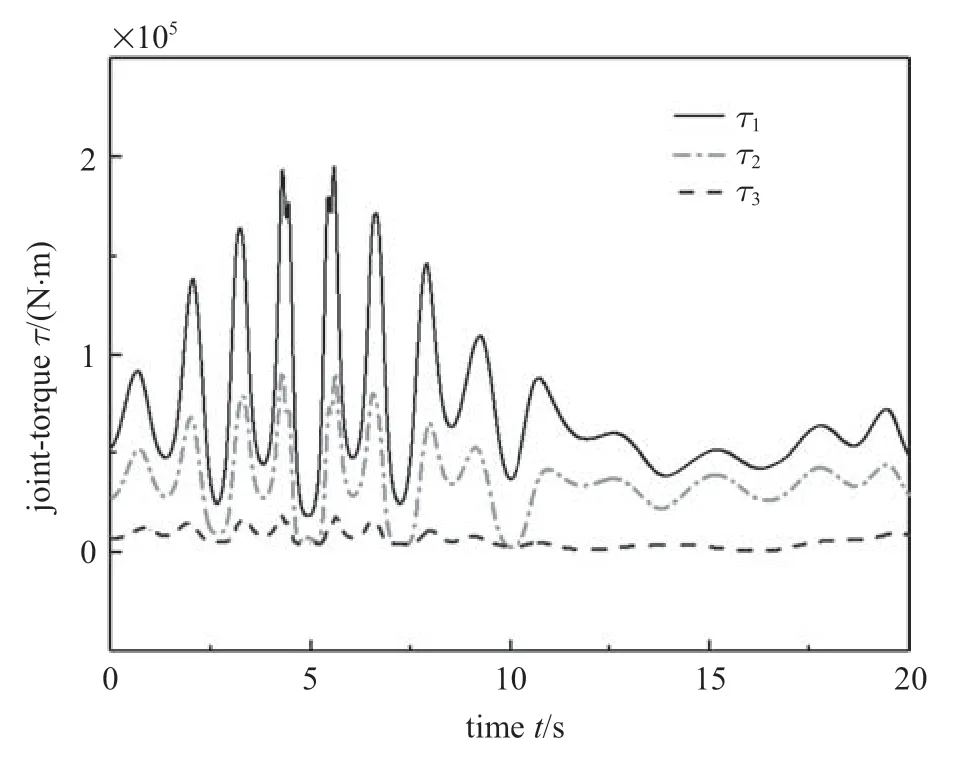
圖15 關(guān)節(jié)力矩Fig.15 The joint-torques

由圖12 和圖15 可見,完成相同指定運動,柔性鉸情況下所需的驅(qū)動力矩小于剛性鉸情況下所需的驅(qū)動力矩.將圖15 力矩施加在柔性鉸系統(tǒng)上,得到柔性鉸的三連桿機械臂運動的位形與圖13 一樣.

4 結(jié)論

本文對考慮鉸阻尼的柔性鉸柔性桿機器人進行動力學建模,推導出包含桿扭轉(zhuǎn)變形、鉸質(zhì)量效應的剛?cè)狁詈蟿恿W方程.并對兩個具體模型進行仿真,得到以下結(jié)論:

(1)隨著柔性鉸剛度的增大,柔性鉸柔性桿機器人的動力學響應幅值減小.

(2)鉸阻尼的存在,會使系統(tǒng)的振動衰減.隨著柔性鉸阻尼的增大,柔性鉸柔性桿機器人的動力學響應衰減變快.

(3)在機器人動力學控制時,鉸的柔性不可忽略.