遵循學(xué)生邏輯走向數(shù)學(xué)邏輯

徐曉良

[摘要]“雞兔同籠”是一線教師非常關(guān)注的一個(gè)熱點(diǎn)教學(xué)內(nèi)容。分析多個(gè)版本教材的“雞兔同籠”，解讀教材編排的意圖，從學(xué)生的調(diào)查問(wèn)卷、訪談中了解學(xué)生的學(xué)習(xí)起點(diǎn)與難點(diǎn)，提出了“雞兔同籠”重組后的學(xué)習(xí)路徑，以促進(jìn)學(xué)生深度學(xué)習(xí)的發(fā)生。

[關(guān)鍵詞]雞兔同籠;邏輯;單元重組

[中圖分類號(hào)]

G623.5

[文獻(xiàn)標(biāo)識(shí)碼]A

[文章編號(hào)] 1007-9068（ 2020）26-0009-04

“雞兔同籠”是人教版教材四年級(jí)下冊(cè)第九單元“數(shù)學(xué)廣角”的內(nèi)容。“雞兔同籠”在我國(guó)古代的數(shù)學(xué)名著《孫子算經(jīng)》中就已經(jīng)出現(xiàn)，為了體現(xiàn)其數(shù)學(xué)文化歷史與獨(dú)特的解決問(wèn)題方法，不同版本的小學(xué)數(shù)學(xué)教材（如人教版、北師大版、蘇教版、青島版等）都把它納入其中。“雞兔同籠”進(jìn)入教材的十幾年里，教師投入了極高的教學(xué)與研究熱情，在百度網(wǎng)頁(yè)輸入“雞兔同籠”四字進(jìn)行搜索，相關(guān)結(jié)果多達(dá)10 700 000個(gè)，可見(jiàn)專家與一線教師對(duì)它的關(guān)注度非常高。但同時(shí)也說(shuō)明了“雞兔同籠”是教學(xué)上的難點(diǎn)，特別是一線教師存在非常多的困惑與疑問(wèn)。通過(guò)對(duì)一線教師的訪談、教材的分析與學(xué)生的調(diào)查問(wèn)卷，給出“雞兔同籠”重組后的學(xué)習(xí)路徑。

一、“雞兔同籠”的教學(xué)困惑

1.復(fù)雜的數(shù)學(xué)問(wèn)題，如何遵循學(xué)生起點(diǎn)？

“雞兔同籠”對(duì)四年級(jí)的學(xué)生來(lái)說(shuō)是一個(gè)非常復(fù)雜的問(wèn)題。復(fù)雜的原因有兩個(gè)：一是很難人手。雖然解法很多，但這些方法都不是平時(shí)解決數(shù)學(xué)問(wèn)題的常用方法。因此，學(xué)生面對(duì)問(wèn)題時(shí)，很難用以前的經(jīng)驗(yàn)來(lái)解決問(wèn)題;二是“假設(shè)法”太抽象。“假設(shè)法”是解決“雞兔同籠”問(wèn)題非常好的數(shù)學(xué)方法，但對(duì)四年級(jí)學(xué)生來(lái)說(shuō)比較陌生，而且解題步驟較多，解題的每一步表示的意思都要很清楚。而小學(xué)四年級(jí)的教材只要求學(xué)生能解決兩步計(jì)算的數(shù)學(xué)問(wèn)題，學(xué)生對(duì)于步驟較多的方法難以理解。因而，如何順著四年級(jí)學(xué)生的學(xué)習(xí)起點(diǎn)，搭起學(xué)生的思維水平與數(shù)學(xué)思想方法之間的橋梁是關(guān)鍵。

2.多樣化的數(shù)學(xué)方法，該面面俱到嗎？

“雞兔同籠”曾經(jīng)是嘉興小學(xué)數(shù)學(xué)團(tuán)隊(duì)研究的一個(gè)內(nèi)容，從一線教師、名優(yōu)教師到知名的特級(jí)教師都親身參與研究，呈現(xiàn)課例。但聽(tīng)完一線教師的課后，都有一個(gè)感覺(jué)——課堂中眉毛胡子一把抓，最后啥都沒(méi)抓住。究竟是什么原因呢？教材呈現(xiàn)的解題方法有畫圖法、列舉法、假設(shè)法、方程法等。但縱觀不同版本教材，“雞兔同籠”無(wú)論編排在哪個(gè)年級(jí)，教材對(duì)于該年級(jí)的學(xué)生所能采用的方法都進(jìn)行了呈現(xiàn)。的確，每種方法都對(duì)應(yīng)著不同的價(jià)值，但這么多種方法都要在一節(jié)課中呈現(xiàn)嗎？都要求學(xué)生掌握嗎？從實(shí)際情況來(lái)看，教師上得手忙腳亂，但學(xué)生還是一知半解。如果不需要面面俱到或是需要梯度呈現(xiàn)，那么面對(duì)四年級(jí)的學(xué)生，雞兔同籠問(wèn)題的落腳點(diǎn)和切人點(diǎn)又在哪里呢？

3.學(xué)生的兩極分化，如何滿足不同學(xué)生的需求？

在雞兔同籠問(wèn)題的教學(xué)中，往往會(huì)出現(xiàn)兩極分化的現(xiàn)象：當(dāng)問(wèn)題呈現(xiàn)時(shí)，學(xué)過(guò)奧數(shù)的學(xué)生立刻用假設(shè)法解題，沒(méi)有接觸過(guò)此類問(wèn)題的學(xué)生就無(wú)從下手。那么面對(duì)全體學(xué)生教學(xué)時(shí)，該如何滿足不同學(xué)生的需求？讓沒(méi)有接觸過(guò)的、能力較弱的學(xué)生如何有法可循？讓學(xué)過(guò)的、能力強(qiáng)的學(xué)生如何深入學(xué)習(xí)，理解“雞兔同籠”問(wèn)題的本質(zhì)？

4.統(tǒng)一編排的教材，如何突破教材編排的順序？

“雞兔同籠”一般是安排兩個(gè)課時(shí)完成相關(guān)教學(xué)，第一課時(shí)是例題學(xué)習(xí)，第二課時(shí)是鞏固練習(xí)。教學(xué)后發(fā)現(xiàn)，許多學(xué)生還是沒(méi)有較好地理解“雞兔同籠”問(wèn)題，一線教師只能通過(guò)增加課時(shí)進(jìn)行相應(yīng)補(bǔ)救，有些教師甚至用了5個(gè)課時(shí)，但最后的效果還是很差。如何突破教材編排的順序，真正讓每個(gè)學(xué)生都能理解并解決“雞兔同籠”問(wèn)題？

帶著這些困惑，深度探究教材編排，從學(xué)生學(xué)習(xí)的起點(diǎn)人手，進(jìn)行了思考、分析、實(shí)踐。

二、知事——“雞兔同籠”問(wèn)題的多版本教材分析

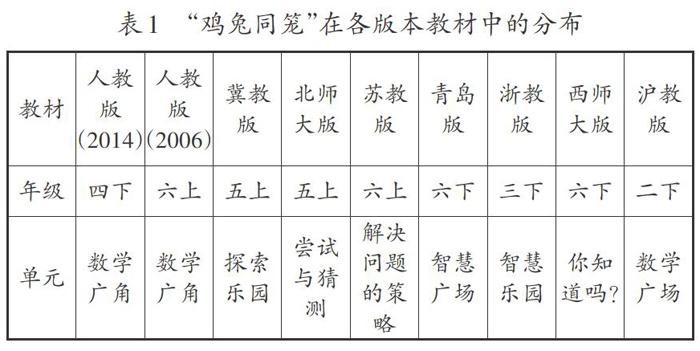
筆者查閱了九個(gè)版本的數(shù)學(xué)教材，發(fā)現(xiàn)“雞兔同籠”問(wèn)題在不同版本的教材中均有編排，但編排的年級(jí)、解決方法介紹及側(cè)重點(diǎn)是不同的（如表1）。

浙教版、西師大版、滬教版教材是將“雞兔同籠”做知識(shí)增量介紹的，其中滬教版教材以“列表枚舉”作為標(biāo)題，借助“雞兔同籠”的素材，側(cè)重列表枚舉方法的學(xué)習(xí);蘇教版、青島版、冀教版、北師大版、2006年與2014年人教版教材將“雞兔同籠”單列單元，作為數(shù)學(xué)廣角中的問(wèn)題解決的內(nèi)容，并采用“例題+練習(xí)”格式呈現(xiàn);蘇教版、青島版教材的例題中均未出現(xiàn)“雞兔同籠”原型題，分別采用了“公園租船問(wèn)題”“停車場(chǎng)問(wèn)題”這樣的生活實(shí)例，再在練一練中加入了“雞兔同籠”原型題、古題等資料。

北師大版和冀教版教材，均以“雞兔同籠”為例題，組織了一個(gè)數(shù)學(xué)主題活動(dòng)。而新、舊人教版教材都將“雞兔同籠”安排在數(shù)學(xué)廣角單元，內(nèi)容充實(shí)，方法多樣，能給學(xué)生提供基本建模和變式提升的空間。 人教版教材將“雞兔同籠”的教學(xué)編排從十一冊(cè)下移到第八冊(cè)，跨度有三個(gè)學(xué)期。在對(duì)比2006年與2014年人教版教材內(nèi)容編排中發(fā)現(xiàn)：編排的內(nèi)容整體變化不大，教學(xué)目標(biāo)定位略有微調(diào)，主要減少了“方程”這種解題思路，其他（含練習(xí)題）則大體相同。

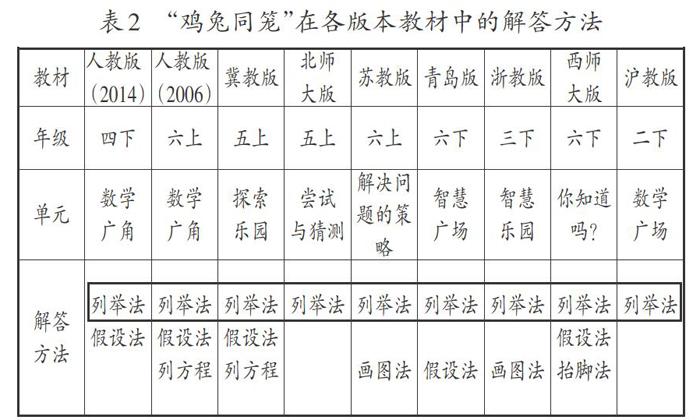
綜合上述對(duì)各版本教材的分析，整理成表2：

不同版本教材安排“雞兔同籠”的年級(jí)不同，學(xué)生學(xué)習(xí)能力差異，教材滲透的解決方法并不完全一致，呈現(xiàn)多樣性，如“列舉法”“畫圖法”“假設(shè)法”“列方程”等。

對(duì)比各版本教材，有兩個(gè)新的思考：

思考一：教材中的諸多方法有聯(lián)系嗎？

教材中呈現(xiàn)的“列舉法…‘畫圖法…‘假設(shè)法…‘列方程”等，表面上都是獨(dú)立的。但深入分析，這些方法之間是有關(guān)聯(lián)的。畫圖法、列舉法、假設(shè)法之間是可以互相轉(zhuǎn)化的：畫圖法是假設(shè)法的具象化，將抽象的假設(shè)法用畫圖的方式，形象地表達(dá)出來(lái);列舉法既可以看作是方程的原型，更可以看作是假設(shè)法的前身，通過(guò)具體數(shù)據(jù)的假設(shè)來(lái)尋找答案。因此，蘇教版、浙教版教材在滲透了畫圖法與列舉法之后，引導(dǎo)學(xué)生總結(jié)對(duì)比兩種方法的聯(lián)系;北師大版教材就以“嘗試與猜測(cè)”為主題，做大做強(qiáng)“列舉法”。

思考二：“列舉法”真的很“土”嗎？

綜觀各版本教材，例題中所要滲透的解決方法多種多樣，但“列舉法”卻是各版本教材所唯一共同采用的解決方法。這是什么原因呢？有許多教師認(rèn)為，列舉法太土了，一一列舉，費(fèi)時(shí)間，效率低。其實(shí)，列舉法是一種重要的數(shù)學(xué)方法，它是研究數(shù)學(xué)常用而本原的方法，但往往因?yàn)樘^(guò)平常而被遺忘。“列舉法”并不“土”，列舉的過(guò)程就是學(xué)生增加數(shù)學(xué)經(jīng)驗(yàn)的過(guò)程，通過(guò)列舉，學(xué)生可以經(jīng)歷“雞兔同籠”方程的完整建模過(guò)程。

在對(duì)多個(gè)版本教材的分析中也發(fā)現(xiàn)，同為“列舉法”，各版本教材在安排上各有側(cè)重。如北師大版教材呈現(xiàn)“一一列舉”列表方法、列表法和“取中列舉”列表法三種解決問(wèn)題的方法。人教版（2014年）偏重“一一列舉”的方法，還加入了特例“8，0”的情況，目的就是銜接假設(shè)法，完善對(duì)“雞兔同籠”問(wèn)題的建模體驗(yàn)。

三、知人——學(xué)生學(xué)習(xí)“雞兔同籠”問(wèn)題的起點(diǎn)分析

對(duì)紫微小學(xué)四年級(jí)5、6兩個(gè)班共88位學(xué)生進(jìn)行了一次前測(cè)，前測(cè)內(nèi)容有兩題：一是“雞兔同籠”原題，二是變式題（共10分鐘）。

第一題：籠子里有若干只雞和兔。從上面數(shù)有8個(gè)頭，從下面數(shù)有26只腳。雞和兔各有幾只？

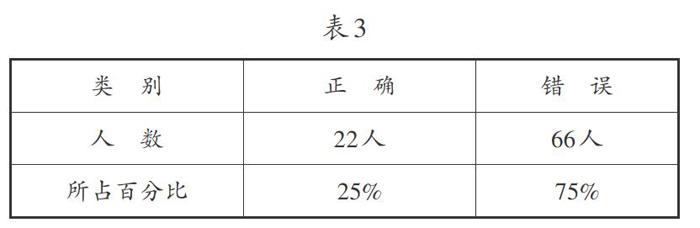
學(xué)生答題的正確率如表3：

第二題：全班一共有38人，共租8條船，大船可以坐6人，小船可以坐4人，每條船都坐滿了。大、小船各有幾條？

學(xué)生答題的正確率如表4：

從統(tǒng)計(jì)結(jié)果可見(jiàn)，無(wú)論是“雞兔同籠”的原題還是變式題，都有四分之一左右的學(xué)生能找到正確答案。那這個(gè)數(shù)據(jù)是不是可以類推到所有班級(jí)呢？答案是否定的。筆者在2018年也對(duì)紫微小學(xué)五（1）班做過(guò)一次前測(cè)，前測(cè)的正確率高達(dá)74.3%，筆者再對(duì)農(nóng)村一所小學(xué)的四年級(jí)做前測(cè)，正確率不到5%。這充分說(shuō)明了班級(jí)之間存在很大的差異。是什么原因造成了這么大的差異？筆者認(rèn)為，課前的學(xué)習(xí)，特別是課外奧數(shù)輔導(dǎo)班的學(xué)習(xí)是造成差異的主要因素。如：前測(cè)的88位學(xué)生中，就有42%的學(xué)生表示在奧數(shù)班中學(xué)習(xí)過(guò)“雞兔同籠”問(wèn)題，而農(nóng)村小學(xué)的學(xué)生只有個(gè)別接觸過(guò)奧數(shù)。

在對(duì)88位學(xué)生的訪談中發(fā)現(xiàn)，有42%的學(xué)生表示以前學(xué)過(guò)，但學(xué)過(guò)的學(xué)生正確率只有25%，從42%至25%的變化，印證了一線教師一直以來(lái)的苦惱：對(duì)四年級(jí)學(xué)生而言，“雞兔同籠”問(wèn)題真的是有難度的！學(xué)習(xí)過(guò)的學(xué)生中也有很大一部分學(xué)生不會(huì)做，沒(méi)學(xué)過(guò)的學(xué)生更是束手無(wú)策。可見(jiàn)，除了班級(jí)間的差異外，班級(jí)內(nèi)部學(xué)生對(duì)于“雞兔同籠”問(wèn)題原有的基礎(chǔ)也呈現(xiàn)兩極分化。因此，對(duì)于“雞兔同籠”問(wèn)題的起始教學(xué)需要低起點(diǎn)、低難度！

做對(duì)的學(xué)生都是采用什么方法？第一題做對(duì)的學(xué)生采用的方法如表5：第二題做對(duì)的學(xué)生采用的方法如表6：

對(duì)于典型題，做對(duì)的學(xué)生一般采用的是假設(shè)法，而對(duì)于變式題，采用假設(shè)法的學(xué)生人數(shù)卻減少了近一半，為什么會(huì)這樣？這樣的數(shù)據(jù)或多或少說(shuō)明了那5個(gè)學(xué)生對(duì)于假設(shè)法是一知半解的。在整理學(xué)生的作品中，又看到了好幾張這樣的作品：接觸過(guò)假設(shè)法、有假設(shè)法的解題模型，但不理解假設(shè)法的真正內(nèi)涵;可能還能解決“雞兔同籠”原題，但變式題就用不了了。

可喜的是，對(duì)于變式題，有學(xué)生嘗試列舉，而且做對(duì)了，做錯(cuò)的學(xué)生中也有很多學(xué)生開(kāi)始去列一列、試一試，即使沒(méi)有找到正確答案。這印證了筆者的一個(gè)想法：很多學(xué)生心中是有列舉嘗試的意識(shí)的，是有這顆種子的。可是學(xué)完“雞兔同籠”的內(nèi)容之后又有多少學(xué)生還會(huì)用列舉法呢？即使沒(méi)有學(xué)會(huì)用假設(shè)法，他依然不愿意用列舉這種“笨”方法。

四、潤(rùn)慧——“雞兔同籠”單元重組學(xué)習(xí)路徑

基于對(duì)教材和學(xué)生的分析，筆者想做的并不是學(xué)生學(xué)完“雞兔同籠”后清一色用假設(shè)法，而是想讓不同的學(xué)生都有不同的層次提升。在學(xué)習(xí)中，讓沒(méi)有接觸過(guò)的、能力較弱的學(xué)生在束手無(wú)策時(shí)，有法可循;讓有一定學(xué)習(xí)基礎(chǔ)、一知半解的學(xué)生想套用模型時(shí)，真正理解;讓已經(jīng)掌握了的、能力較強(qiáng)的學(xué)生在正確解答時(shí)，深度理解。具體安排如表7：

1.回歸原始，做強(qiáng)、做大“列舉法”

從解題方法的角度而言，方程法遠(yuǎn)比畫圖、列表之類的方法要快捷簡(jiǎn)便，但這種快捷簡(jiǎn)便是數(shù)學(xué)的價(jià)值而不是教育的價(jià)值！對(duì)于數(shù)學(xué)廣角的內(nèi)容，對(duì)于學(xué)生學(xué)習(xí)的價(jià)值，不僅僅只是得到一個(gè)答案和結(jié)果，更多的是要給予學(xué)生面對(duì)新的、未知的問(wèn)題該如何解決的一種方法和策略的指引：面對(duì)新問(wèn)題如何人手？從哪里人手？怎么進(jìn)行嘗試？怎樣在嘗試的過(guò)程中發(fā)現(xiàn)和總結(jié)？因此，通過(guò)重組，在課堂上讓學(xué)生回歸到學(xué)習(xí)的最原始狀態(tài)，嘗試用畫一畫、舉一舉的方法解決問(wèn)題，在解決問(wèn)題的過(guò)程中慢慢積累經(jīng)驗(yàn)，一步一步地優(yōu)化、提升經(jīng)驗(yàn)，放慢腳步，做強(qiáng)、做大列舉法和畫圖法。在這一過(guò)程中，學(xué)生的有序思考、觀察、分析、歸納、創(chuàng)新、發(fā)現(xiàn)等綜合能力都得到了發(fā)展，數(shù)學(xué)核心素養(yǎng)得到了培養(yǎng)。

2.拉長(zhǎng)過(guò)程，做深做厚“假設(shè)法”

面對(duì)兩極分化相對(duì)比較嚴(yán)重的“雞兔同籠”問(wèn)題，重組后的第一課時(shí)貌似忽略了“優(yōu)秀學(xué)生”的存在，但這并不是放棄假設(shè)法，而是拉長(zhǎng)體驗(yàn)的過(guò)程，給假設(shè)法做了更深更厚的鋪墊。課堂上難免有優(yōu)秀學(xué)生會(huì)提出假設(shè)法，而太快得出了如此“簡(jiǎn)易而通吃”的方法，往往會(huì)忽視結(jié)果背后的產(chǎn)生過(guò)程。假設(shè)全是雞或兔，逼近的思想在畫圖法、列表法中都有滲透，拉長(zhǎng)這個(gè)過(guò)程，就能給予“沒(méi)有接觸過(guò)或能力弱的學(xué)生”一個(gè)理解的機(jī)會(huì)，給予“貌似理解假設(shè)法的學(xué)生”一個(gè)走進(jìn)假設(shè)法背后的機(jī)會(huì)。而且，第一課中的兩個(gè)例題都不是典型的“雞兔同籠”問(wèn)題，而是用三角形與五邊形、5角與2角這樣的素材，進(jìn)一步避免了部分學(xué)生套用公式，使學(xué)生從本質(zhì)上來(lái)理解這些數(shù)學(xué)問(wèn)題。

3.溝通融合，做透、做活“綜合法”

本單元的重組中，實(shí)現(xiàn)了兩次溝通融合。第一次的溝通融合是在第一課時(shí)中，例1要求學(xué)生完整列舉，將所有情況有序地寫出來(lái)。例2引導(dǎo)學(xué)生思考：找到正確答案后，還需要列舉下去嗎？通過(guò)討論發(fā)現(xiàn)，找到正確答案后，不需要再列舉下去了，再往下列舉要么是多相關(guān)數(shù)，要么少相差數(shù)。對(duì)于例3，要求學(xué)生快速列舉。這時(shí)，學(xué)生在已有的經(jīng)驗(yàn)基礎(chǔ)上，開(kāi)始跳躍式的列舉，從隨意舉2個(gè)數(shù)后根據(jù)相差數(shù)快速調(diào)整出正確的答案，而快速調(diào)整的過(guò)程已經(jīng)是假設(shè)法的雛形了。第二次融合在第二課時(shí)，在教學(xué)了假設(shè)法后，再引導(dǎo)學(xué)生比較列舉法與假設(shè)法，學(xué)生突然發(fā)現(xiàn)列舉法就是假設(shè)法，只不過(guò)假設(shè)法是從特殊的數(shù)字開(kāi)始，而列舉法是從普通的情況開(kāi)始，而本質(zhì)不變的是關(guān)注總數(shù)的相差數(shù)與兩種不同物體的相差數(shù)。這兩個(gè)層面的溝通融合，會(huì)讓學(xué)生頓悟，讓學(xué)生豁然開(kāi)朗。

（責(zé)編金鈴）