THE α-BERNSTEIN OPERATOR OF A LIPSCHITZ CONTINUOUS FUNCTION

LIU Zhi,WANG Chu-han,CHEN Xiao-yan,TAN Jie-qing

(School of Mathematics,Hefei University of Technology,Hefei230009,China)

Abstract:The relationship between the α-Bernstein operator and its approximation function is discussed in this paper.If the α-Bernstein operator belongs to the class of Lipschitz functions,then its approximation function f(x)also does,and vice versa.Moreover,the α-Bernstein operator can maintain the Lipschitz constant of the original function.

Keywords:function approximation;α-Bernstein operators;Lipschitz continuity;Lipschitz functions

1 Introduction

In 1885,Weierstrass published his famous theorem asserting that every continuous function in a compact interval of the real line is the uniform limit of a sequence of algebraic polynomials in[1].Several different proofs of Weierstrass’s theorem are known,but a remarkable one was given by Bernstein[2]in 1912.As a generalization of the Bernstein operator,theα-Bernstein operator proposed by Chen in[3]has almost the same approximation property as the Bernstein operator.

Suppose a functionf(x)is continuous on[0,1].Thenth(n≥1)α-Bernstein operator off(x)is denoted and defined bywhereand 0≤ α ≤1.Fori=0,1,···,n,theα-Bernstein polynomialof degreenis defined byand whenn≥2,

Obviously,Tn,α(f;x)is an algebraic polynomial of degree no greater thannand its importance in approximation theory arises from the fact thatuniformly on[0,1].Whenα=1,theα-Bernstein polynomial reduces to the classical Bernstein polynomial,i.e.,

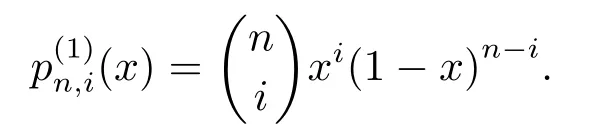
So theα-Bernstein operator has following identity

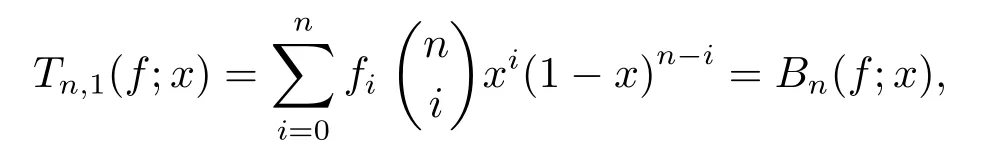
which means that the class ofα-Bernstein operators contains the classical Bernstein ones.

α-Bernstein operators are given explicitly and depend only on the values of a function for rational values of the variable.They have various shape-preserving properties and are easy to handle in computer algebra systems and these are very useful when the evaluation offis difficult and time-consuming.One of the outstanding properties of these polynomials is that they mimic the behavior of the given functionf(x)to a remarkable degree.Some results that hold for continuous functions,e.g.,an upper bound for the error is obtained in terms of the usual modulus of continuity.However,there are special classes of functions for which better estimates can be given.Thus,we consider the case of Lipschitz functions.

Lipschitz continuity,named after German mathematician Rudolf Lipschitz,is a strong form of uniform continuity for functions.In the theory of differential equations,Lipschitz continuity is the central condition of the Picard-Lindelf theorem which guarantees the existence and uniqueness of the solution to an initial value problem.A special type of Lipschitz continuity,called contraction,is used in the Banach fixed point theorem.We have the following chain of inclusions for functions over a closed and bounded interval:continuously differentiable?Lipschitz continuous?uniformly continuous=continuous.

A real-valued functionf(x):[0,1]→R is called Lipschitz continuous or to satisfy a Hlder condition of orderβ∈(0,1]if there exists a positive real constantMsuch that for every pair of pointsx1,x2∈[0,1],

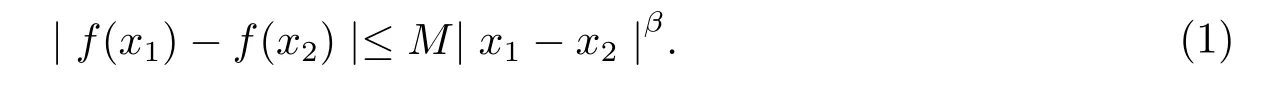
Obviously,a Lipschitz continuous function must be a continuous function for allβ∈(0,1].Intuitively,a Lipschitz continuous function is limited in how fast it can change whenβ=1:there exists a real number such that,for every pair of points on the graph of this function,the absolute value of the slope of the line connecting them is not greater than this real number.An everywhere differentiable function is Lipschitz continuous if and only if it has bounded first derivative.Iff(x)∈LipMβ,thenf(x)is uniformly continuous.

Several proofs are known for the remainder in approximations of Lipschitz functions by Bernstein operators.Kac considered these classes in[4–5].In 1987,Brown et al.[6]gave an elementary proof that the Lipschitz constant is preserved,i.e.,iff(x)∈LipMβ,then forn=1,2,···,Bn(f;x)∈LipMβalso.The caseβ=1 was considered by Hajek in[7]and the general case was studied in[8](another more complicated proof,using probabilistic methods was given in[9]).

The objective of this paper is to prove that theα-Bernstein operator belongs to the class of Lipschitz functions,then its approximation functionf(x)also does,and vice versa.

2 Main Lemma

For convenience of description,theα-Bernstein operator forf(x)is usually expressed asTn,α(f;x)=(1?α)Gn(f;x)+αBn(f;x),where

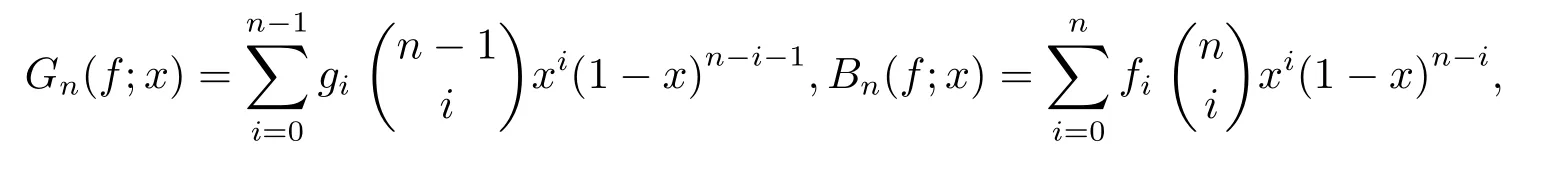
and

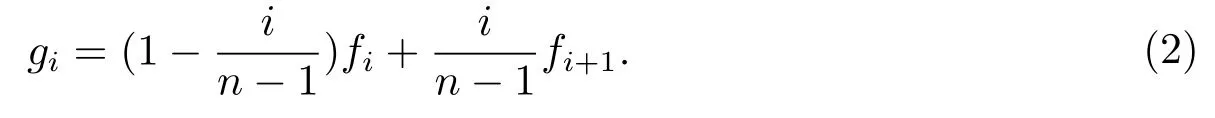
Lemma 1Iff(x)∈LipMβ,then forn=1,2,···,i,j,i+j=0,1,···,n?1,

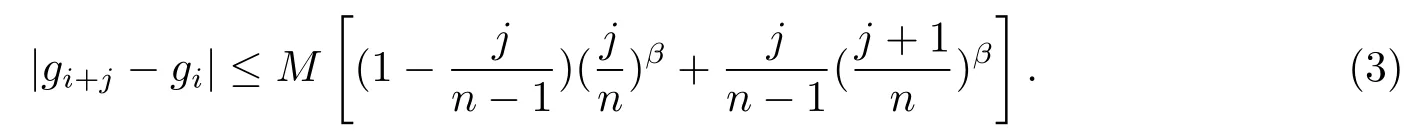
ProofIt easily follows from(1)that

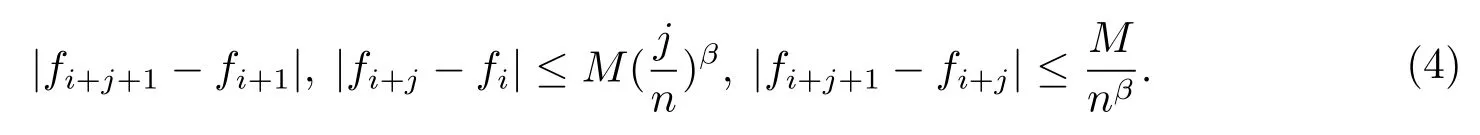
It follows from(2)that

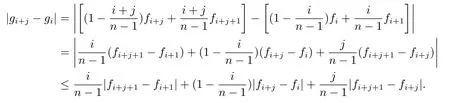
Substituting(4)into the above inequality,we can obtain

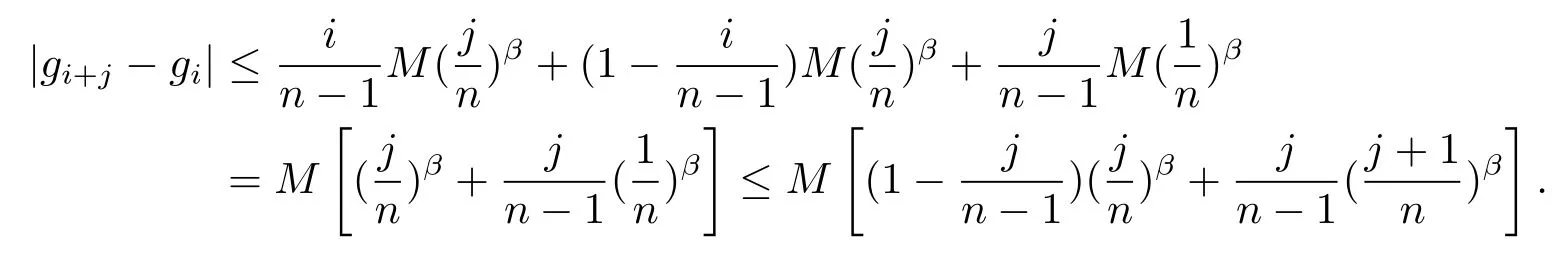
In fact,the last inequality above is equivalent tojβ+1≤(j+1)β,and Lemma 1 is proved.

Lemma 2Iff(x)is convex on[0,1],thenTn,α(f;x)≥f(x)for allx∈[0,1]andn≥1.

ProofFor eachx∈[0,1],let us define0≤r≤n.We see thatλr≥0 whenx∈[0,1],and note fromTn,α(1;x)=1 andTn,α(x;x)=x,respectively,thatThen we obtain sincef(x)is convex on[0,1],

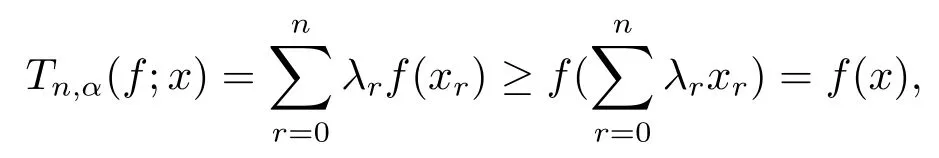
and this completes the proof.

Lemma 3Forf(x)=xβ,0<β≤1 and forn=1,2,···,Tn,α(xβ;h)≤hβ,0≤h≤1.

ProofAs a consequence of Lemma 2,we have,since the functionf(x)=?xβ,0<β≤1,is convex on[0,1],that forn=1,2,···,Tn,α(?xβ;x)≥?xβ.It follows fromTn,α(?xβ;x)=?Tn,α(xβ;x)thatTn,α(xβ;x)≤xβ,n=1,2,···.This completes the proof.

3 Main Result

One of the most interesting connections between direct and converse results forα-Bernstein operator like the classic operator is given in Theorem 1.The following theorem is the main result of this paper.

Theorem 1Fixβ∈(0,1],M>0,andf∈C[0,1].The following assertions are equivalent

(i)f(x)∈LipMβ.

(ii)For anyn≥1,Tn,α(f;x)∈LipMβ.

Proof(i)?(ii)Fix pointsx1,x2∈[0,1],x1≤x2.We use the representation

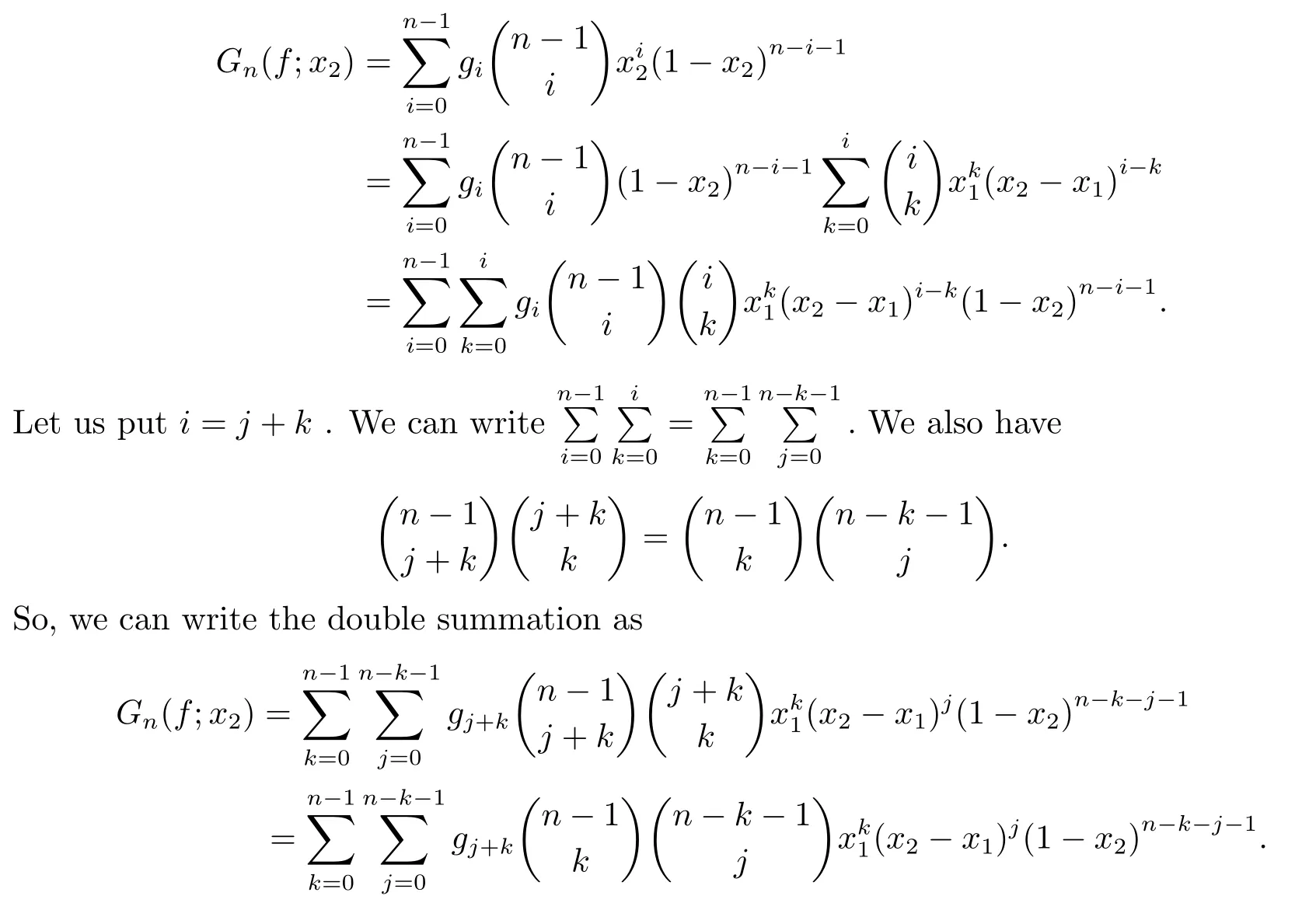
It follows from(3)that

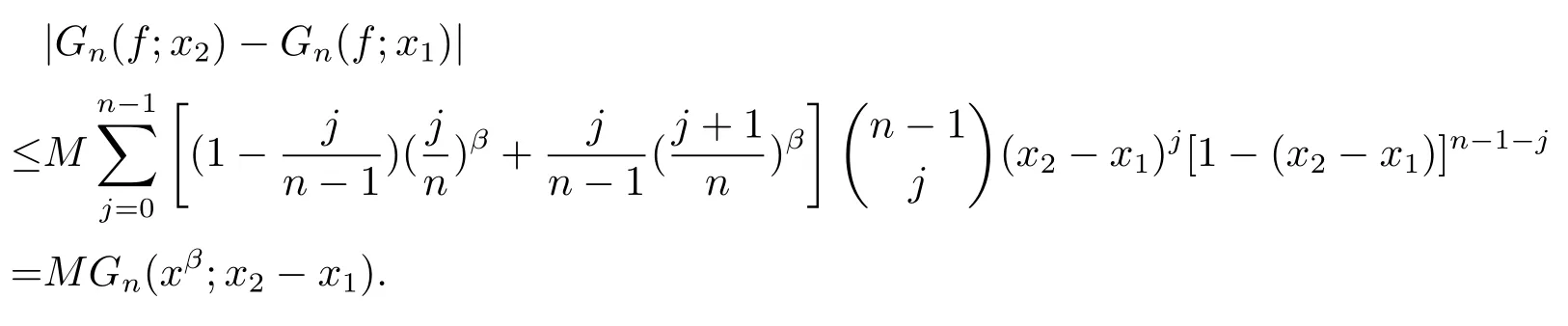
In the same way,we also have

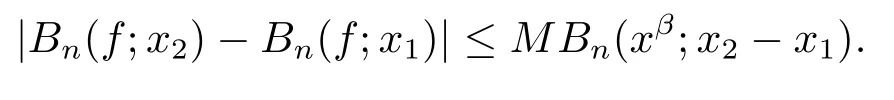
From the two inequalities obtained above,forx1≤x2,one has

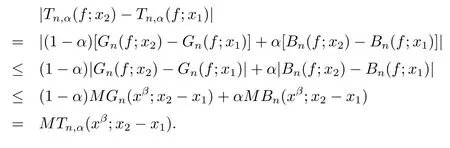
It follows from Lemma 3 that|Tn,α(f;x2)?Tn,α(f;x1)|≤M(x2?x1)β,whereMis the Lipschitz constant off.Thus,we see thatTn,α(f;x)∈LipMβ.

(ii)?(i)Fixf∈C[0,1]and assume that,forx1,x2∈[0,1]and anyn∈N,

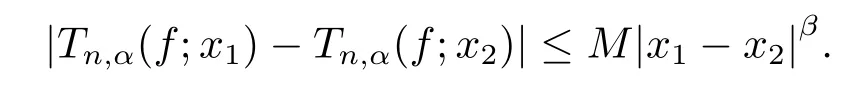
And givenε>0,there must beN∈N,such that for anyn>N,.Then

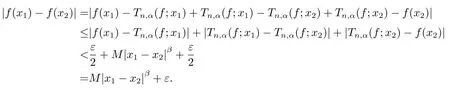
Thus we seef(x)∈LipMβ.This completes the proof.

The interesting thing about this result is that each of theα-Bernstein operatorTn,α(f;x),forn=1,2,···,has the same Lipschitz constant as the given functionfwhen considered as being in the class of functions LipMβ.