INTEGRAL FORMULAS FOR COMPACT SUBMANIFOLDS IN EUCLID SPACE
WANG Qi,ZHOU Zhi-jin
(School of Mathematics and Information Science,Guiyang University,Guiyang 550005,China)
Abstract:In this paper,we study the problem of integral formulas for an oriented and compact n-dimension isometric immersion submanifold Mnwithout boundary in the(n+p)-dimension euclid space Rn+p.At first,we define the r-th higher order mean curvature Hr(0≤r≤n)along the direction of the unit mean curvature vector field ξ to Mn,and then we attain a new integral formula,by applying the method of moving frame and exterior differential,which generalizes a classical integral formula in the case of codimension p=1,that is in the case of hypersurfaces.
Keywords:euclid space;compact submanifold without boundary;mean curvature vector field;higher order mean curvature;integral formula
1 Introduction
It is well known that study on hypersurfaces and submanifolds in euclid space is one of fundamental tasks of differential geometry.For oriented and compact isometric immersion hypersurfaces in euclid space,references[1–3]ever established a classical integral formula,that is the following Theorem 1.1.
In this paper,we study an oriented and compactn-dimension isometric immersion submanifoldMnin the(n+p)-dimension euclid spaceRn+p.Letξbe the unit mean curvature vector field ofMn.At first,we define the higher order mean curvatureHr(r=0,1,2,···,n)along the directionξ.And then,by applying the method of moving frame and exterior differential,we attain a new integral formula,that is the following Theorem 1.2.When codimensionp=1,Theorem 1.2 becomes Theorem 1.1.
Theorem 1.1(see[1–3])Let?:M→Rn+1be an oriented and compact isometric immersion hypersurface without boundary.Then the following integral formulas hold
hereNis the unit normal vector field toM,Hkis thek-th higher order mean curvature ofMandis the euclid inner product inRn+1,dMis then-dimension Riemann volume form forM.
Theorem 1.2Let?:Mn→Rn+pbe an oriented and compactn-dimension isometric immersion submanifold without boundary.Then the following integral formulas hold
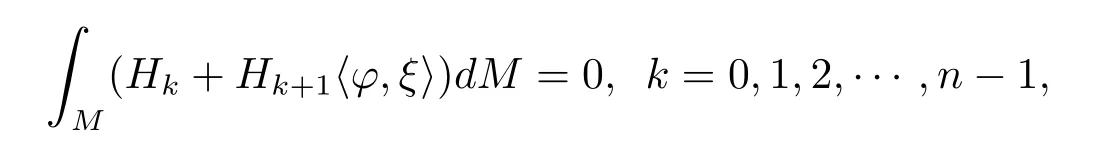
hereξis the unit mean curvature vector field toMn,Hkis thek-th higher order mean curvature along the directionξandis the euclid inner product inRn+p,dMis then-dimension Riemann volume form forMn.
2 Preparation
LetRn+pbe the(n+p)-dimension euclid space and(Mn,g)be a smoothn-dimension Riemann manifold.Denote by?:Mn→Rn+pa smooth immersion mapping between smooth manifolds.If the equationholds everywhere onMn,thenMnor?(Mn)is called an isometric immersion submanifold inRn+p.Hereis the euclid inner product ofRn+pand??is the pull-back mapping for the immersion mapping?.
In this paper,we prescribe the index range as
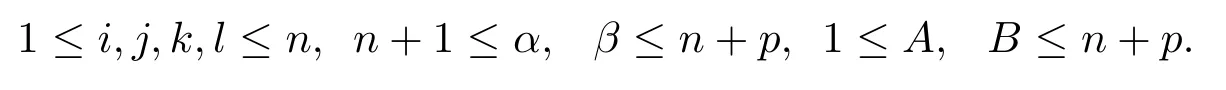
Denote by{eA}a local unit orthogonal frame field forRn+psuch that when being confined ontoMn,{ei}is a local unit tangent frame field toMnand{eα}is a local unit normal frame field toMn.
Denote by{ωA}the dual frame field for{eA},then the second fundamental formIIforMncan be expressed in component form as
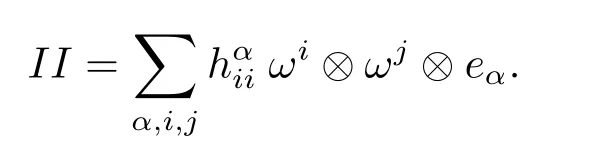
Define the mean curvature vector fieldσtoMnas
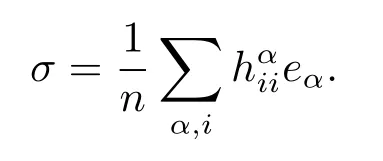
It is well-known that the definition ofσis independent on the choice of the local unit orthogonal frame field{eA}.
We consider the unit mean curvature vector fieldξ=σ/|σ|.Let{λi}be the principal curvature functions along the directionξ,then ther-th higher order mean curvatureHr(r=1,2,...,n)is defined as
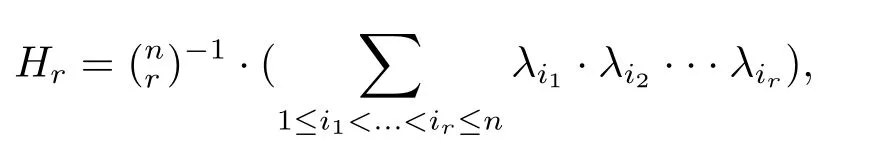
Reference[3]ever attained a fundamental integral formula that is the integral of the Codazzi tensor field on an isometric immersion hypersurface inRn+1.Similar to reference[3],forn-dimension isometric immersion submanifoldMnofRn+p,we attain the following Lemma 2.2.Here we firstly recall some relevant fundamental concepts and properties.Assume thatSis a tensor field of type(k,k)on a Riemann manifold(Mn,g).IfSis anti symmetric both to its each pair of covariant indices and to its each pair of contravariant indices,then we write
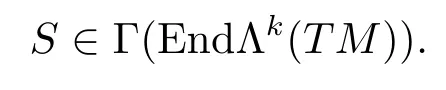
ForS∈Γ(End Λk(TM)),T∈Γ(End Λl(TM)),we also consider the tensor field of type(k+l,k+l),
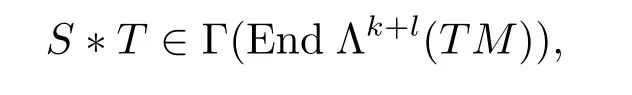
and the definition ofS?Tis that the exterior product of covariant components ofSand the covariant components ofT,and respectively the exterior product of contravariant components ofSand the contravariant components ofT.And by reference[3],this product?is associative and commutative.
Definition 2.1(see[3],Codazzi tensor field)Let(Mn,g)be an-dimension Riemann manifold andS∈Γ(End Λk(TM)).If for allC∞vector fieldX1,X2,···,Xk+1∈Γ(TM)we have
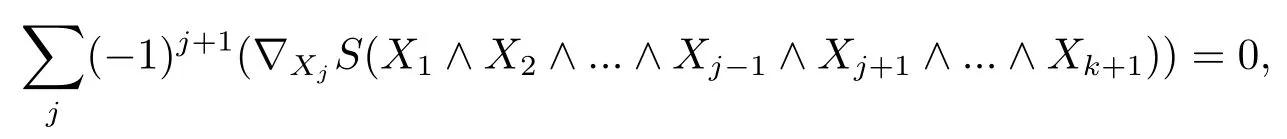
thenSis called a Codazzi tensor field onMn,here?is the Levi-Civita connection of(Mn,g).
According to reference[3],we know that ifSandTare Codazzi tensor field respectively of type(k,k)and type(l,l)on(Mn,g),thenS?Tmust be a Codazzi field tensor field of type(k+l,k+l)onMn.From reference[3],we also define a Codazzi tensor fieldAof type(1,1)onMn.Let(Mn,g)be an-dimension Riemann manifold andψ:Mn→Rn+pbe an isometric immersion mapping.LetYbe the position vector field ofψ(Mn)inRn+p,then the Codazzi tensor fieldAof type(1,1)is determined by
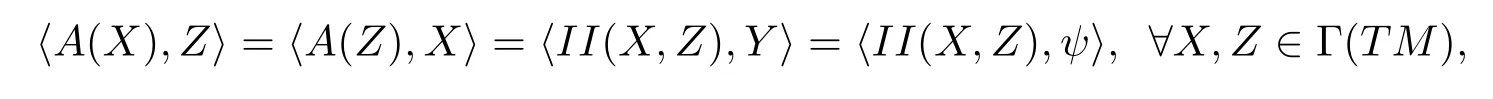
Now we are ready to prove the following Lemma 2.2.
Lemma 2.2let(Mn,g)be an-dimension Riemann manifold andψ:Mn→Rn+pbe an oriented and isometric immersion mapping.Letψ(Mn)be compact and be without boundary.Assume thatSis a Codazzi tensor field of type(k,k)onMn,then the following integral formulas hold
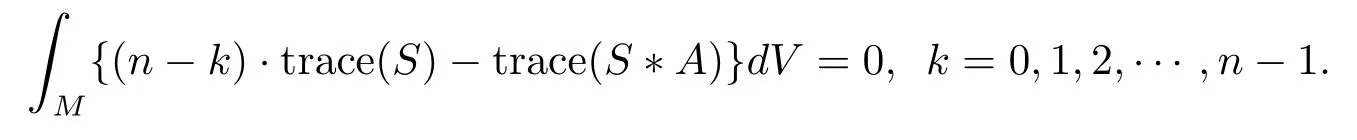
HeredVis then-dimension Riemann volume form ofMnandtraceis the trace operator.
ProofDenote bydVthen-dimension Riemann volume form ofMn,then the following equation
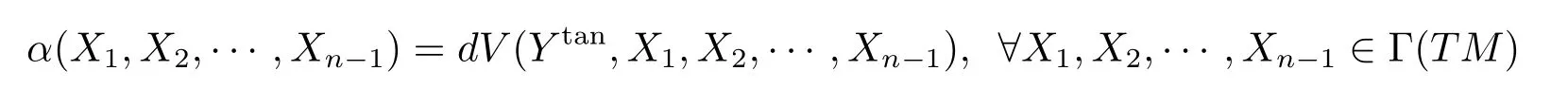
determines a(n?1)form and it is written ashereYtanis the tangent component toMnof the position vectorYforψ(Mn)inRn+p.
From reference[3]and direct computation,we have
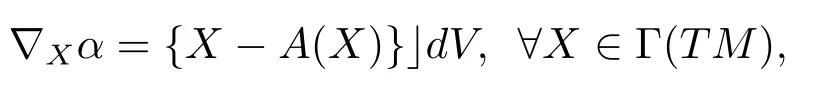
here?is the Levi-Civita connection of(Mn,g).At first we assume thatSis a Codazzi tensor field of type(n?1,n?1).
Let{ei}is an unit orthogonal frame forMnand write

We can seeω=α?Sas a(n?1)form which takes value in Γ(End Λk(TM).By the computation in reference[3],we have
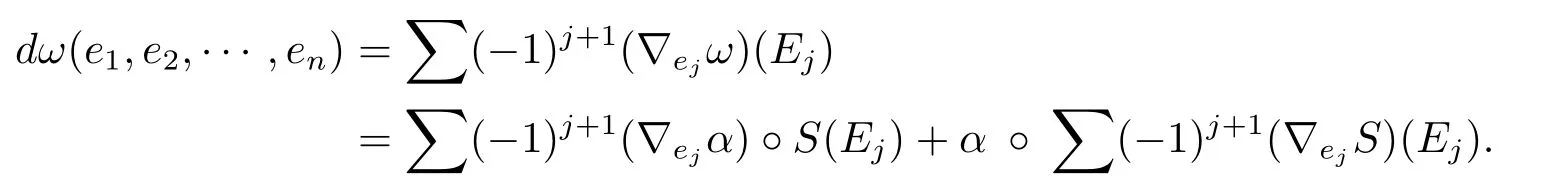
BecauseSis a Codazzi tensor field,the second term of the above equation vanishes and so we have
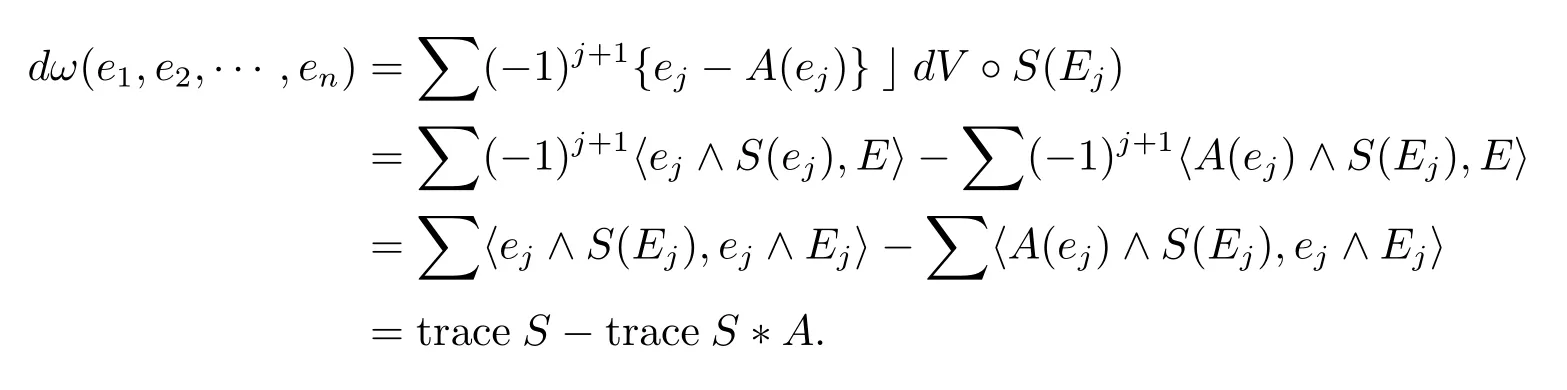
BecauseMnis compact and is without boundary,And so Lemma 2.1 holds in the case thatSis a Codazzi tensor field of type(n?1,n?1).Now we assume thatSis a Codazzi tensor field of type(k,k).Denote byIthe identity element of Γ(End Λn?k?1(TM)).
BecauseIis parallel,I?Sis a Codizza tensor field of type(n?1,n?1).So from the above conclusion we have
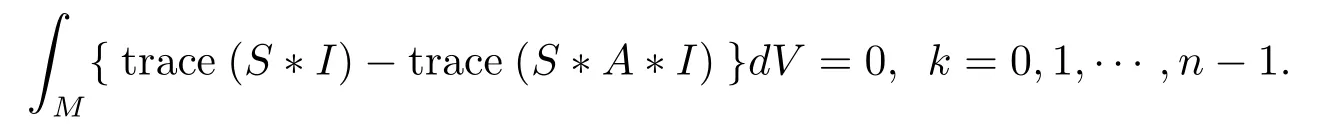
Finally we notice that
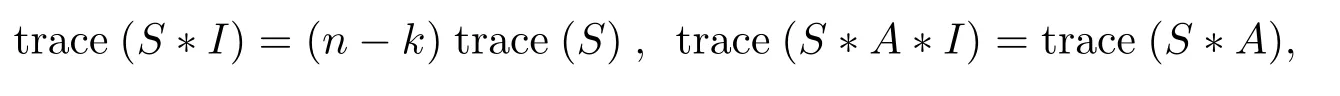
we already finish the proof of Lemma 2.2.
3 Proof of Theorem 1.2
Theorem 1.2Let?:Mn→Rn+pbe an oriented and compactn-dimension isometric immersion submanifold without boundary.Then the following integral formulas hold.
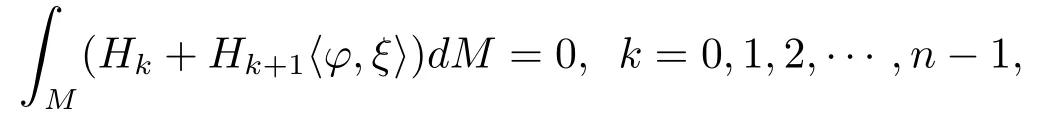
hereξis the unit mean curvature vector field toMn,Hkis thek-th higher order mean curvature along the directionξandis the euclid inner product inRn+p,dMis then-dimension Riemann volume form forMn.
ProofLetTξbe the shape operator ofMnalong the direction of the unit mean curvature vector fieldξ,that is to say,Tξis a tensor field of type(1,1)onMndefined by
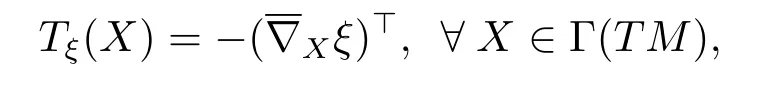
hereis the Levi-Civita connection ofRn+p.
Because the Levi-Civita connectionis flat,by the Codazzi equation for submanifold(see[4]),we know thatTξis a Codazzi tensor field of type(1,1)onMn.
Denote byλ1,λ2,···,λnthe characteristic values ofTξand byσrther-th fundamental homogeneous symmetry polynomial,that is
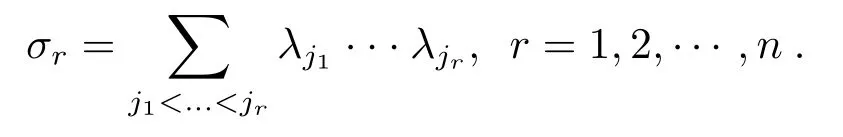

Denote by
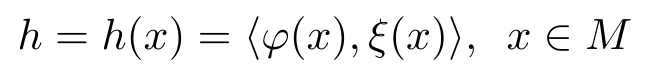
the support function ofMnalong the directionξ.Then it is easy to seeA=?hTξ.By direct computation,we have
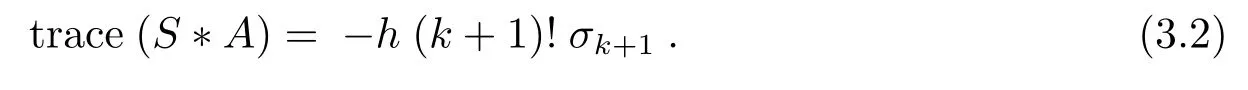
Now we recall once again the definition of the higher order mean curvatureHralong the unit mean curvature vector fieldξ
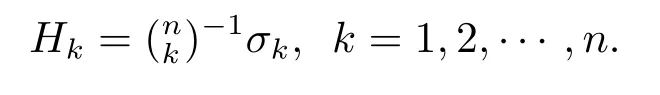
We notice the above(3.1),(3.2)and then we apply Lemma 2.2,we already finish the proof for Theorem 1.2.
- 數(shù)學(xué)雜志的其它文章
- 完整Coriolis力與弱地形作用下的非齊次mKdV-Burgers方程
- 有窮平坦維數(shù)的同調(diào)轉(zhuǎn)換刻畫(huà)
- 正合范疇的整體Gorenstein維數(shù)
- S3中等參曲面的兩個(gè)特征
- FEKETE-SZEG PROBLEMS FOR SEVERAL QUASI-SUBORDINATION SUBCLASSES OF ANALYTIC AND BI-UNIVALENT FUNCTIONS ASSOCIATED WITH THE DZIOK-SRIVASTAVA OPERATOR
- NONCONFORMING FINITE ELEMENT METHOD FOR THE NONLINEAR KLEIN-GORDON EQUATION WITH MOVING GRIDS

