公路橋梁墩柱豎直度檢測與評價

甯家成，謝應爽

(重慶市公路工程質量檢測中心，重慶 400060)

0 前 言

隨著交通強國戰略的推進，高等級公路建設不斷加密，大跨徑高墩橋梁越來越多。對高墩橋梁而言，橋梁墩柱豎直度關系重大，嚴重影響橋梁結構受力，影響橋梁結構安全和使用壽命。

橋梁墩柱豎直度檢測主要用于施工過程控制和交工驗收對墩柱初始狀態檢測評價。橋梁墩柱豎直度檢測方法主要有垂線法和全站儀測量法。研究發現，常規的豎直度檢測只針對墩柱底和墩柱頂兩個斷面的特征計算水平偏移和傾斜率，不能檢測出墩柱中心軸線的空間線形。同時橋梁墩柱施工的初始傾斜、承臺或基樁下沉、外部荷載作用和表面凹凸現象引起傾斜或傾斜假象，不能有效區分和排除[1]。因此，亟需在原有方法的基礎上進行改進。

本文結合實踐經驗對垂線法、全站儀檢測圓柱墩和矩形墩的豎直度進行了總結分析和改進，并采用最小二乘法計算豎直度參數，提高了結果的精度和可靠性。

1 垂線法

垂線法較常見的是在墩柱頂部位置上，直接或支出一點懸掛適當重量的垂球，在垂線上下部讀取(采用網格讀書板時)或量出觀測點的水平位移。計算上下兩點位移差，并記錄位移方向。

垂線法除懸掛垂球外，也可用激光垂準儀發射激光束做參考垂線。檢測時激光垂準儀務必嚴格整平、對中，保證激光束鉛垂。

公路工程質量檢驗評定標準要求檢查縱、橫兩個方向豎直度。故采用垂線法檢測時分別在縱橋向和橫橋向兩個不同方向吊垂球或架設激光垂準儀，測量墩柱頂相對墩柱底的位移偏移量。垂線法檢測豎直度示意如圖1，具體步驟如下。

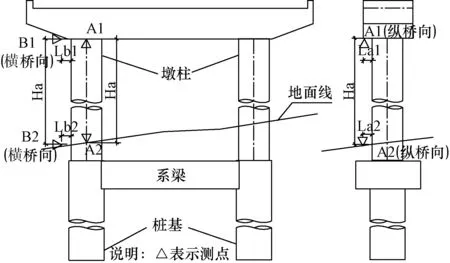
圖1 垂線法檢測豎直度示意圖

1.1 數據采集

測量縱橋向偏移值時，分別測量上吊點(或垂準儀激光光斑)與縱橋向測點A1的距離La1，下吊點(或垂準儀架設中心)與縱橋向測點A2的距離La2。同時測量測點A1和測點A2的距離Ha。

測量橫橋向偏移值時，分別測量上吊點(或垂準儀激光光斑)與橫橋向測點B1的距離Lb1，下吊點(或垂準儀架設中心)與橫橋向測點B1的距離Lb2。同時測量測點B1和測點B2的距離Hb。

1.2 數據計算分析

縱橋向偏移值：δ1=La1-La2，檢測高度Ha，方向根據δ1正負判斷；橫橋向偏移值：δ2=Lb1-Lb2，檢測高度Hb，方向根據δ2正負判斷。

垂線法原理簡單，但一般只能反映頂部底部特征點傾斜情況，對成橋狀態的墩柱豎直度檢測時常需要橋檢車配合，若采用垂球吊垂線，對于高墩柱或多風地區，垂球會擺動干擾較大。采用激光垂準儀檢測雖精確度高，但部分橋梁墩柱施工完成后底部已不具備架設儀器的條件。故垂線法常用于施工過程檢測，或高度較低的墩柱豎直度檢測。

2 全站儀法

隨著測量技術的發展和精度的提高，全站儀自動化程度越來越高，搭載的面向用戶使用程序越來越多。其中包括自由設站功能和免棱鏡無接觸測點功能，這使得采用全站儀測量橋梁墩柱豎直度更為方便快捷和準確可靠。公路橋梁中墩柱截面的形式多為圓形或矩形。下面分別介紹采用全站儀測量圓形墩柱和矩形墩柱的豎直度方法。

2.1 圓形墩柱的豎直度檢測

對圓形墩柱首先利用全站儀的自由設站功能，通過參考點建立縱橋向、橫橋向的坐標系，再快速采集墩柱上中下多個斷面的圓柱體坐標，每個斷面各采集3個以上的點坐標(常取4個點，位置分開不重合)，再計算出各斷面圓心坐標和總高差[2]。通過對圓心坐標擬合得墩柱變形曲線，進而計算出墩柱的傾斜量和傾斜方位。圓形墩柱豎直度檢測示意如圖2，具體步驟如下。

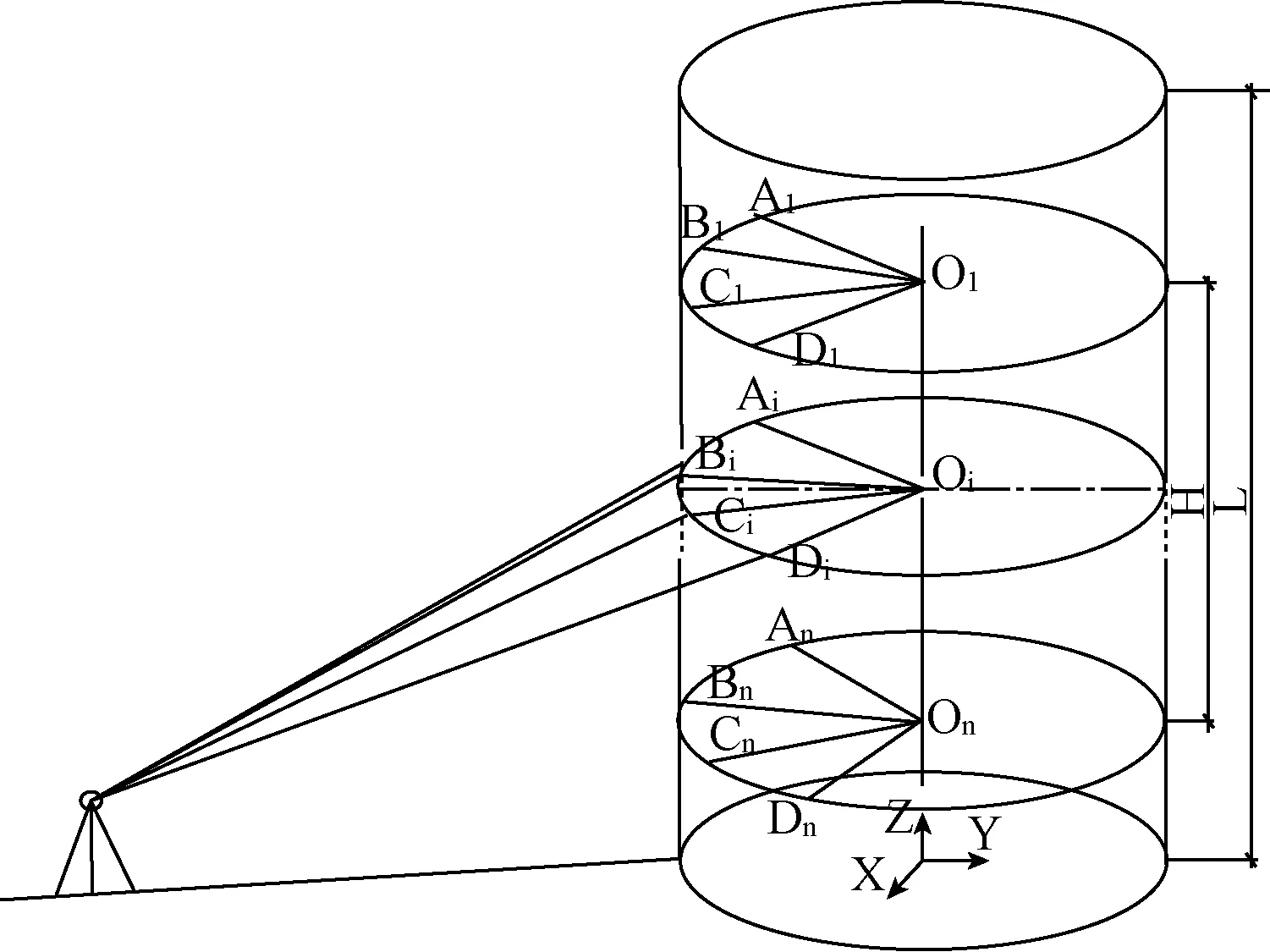
圖2 圓形墩柱豎直度檢測示意圖

2.1.1 數據采集

1)建立檢測坐標系：選擇合適位置架設儀器(一次盡可能檢測多個墩柱)，通過參考點給全站儀建立橫橋向和縱橋向的測站。可以路線前進方向(縱橋向)為X軸正方向，面向路線前進方向橫橋向左側為Y軸正方向，鉛垂向上為Z軸正方向。

2)特征斷面點坐標測量：根據墩柱高度，除靠頂部和底部的斷面外，在墩身大致均勻布置若干(一般2個)能反應墩柱特征的柱坐標采集斷面。在測站建好后，采用無棱鏡點坐標測量模式，測量各采集斷面4個不同點Ai、Bi、Ci、Di的坐標(xi1，yi1，zi1)，(xi2，yi2，zi2)，(xi3，yi3，zi3)，(xi4，yi4，zi4)。

2.1.2 數據計算分析

1)計算圓心坐標：根據各特征斷面點Ai、Bi、Ci、Di坐標計算圓心Oi坐標(Xi，Yi，Zi)。由于誤差，Ai、Bi、Ci、Di四個點，并不完全在同一個圓周上，且高程坐標也存在細微差異。計算時4個點視為在同一高度，Zi取4個點高程的平均值。根據3個點可以確定一個圓，故通過4個點中每3個點的x,y坐標均計算得一個圓心坐標，最后取平均值作為該斷面圓心Oi的坐標。

2)根據圓心坐標擬合墩柱變形曲線：求出圓心坐標后，根據X1、X2、……、Xn和對應高程坐標，按墩柱變形規律采用最小二乘法擬合出墩柱縱橋向的變形曲線。墩柱變形曲線近似為二次拋物線，故可采用拋物線基本方程X=A1Z2+B1Z+C1按最小二乘法擬合。其中系數A1、B1、C1為如下三元一次方程組的解。

同理，根據Y1、Y2、……、Yn和對應高程坐標，按最小二乘法擬合得橫橋向變形曲線方程Y=A2Z2+B2Z+C2。

3)計算墩柱偏移值：縱橋向偏移值δ1=X(Z1)-X(Zn)；橫橋向偏移值δ2=Y(Z1)-Y(Zn)；根據取值的正負判斷偏位的方向。

2.2 矩形墩柱的豎直度檢測

矩形墩柱由于自身存在相互垂直面，故用本身點便可方便建立縱、橫橋方向坐標系，無需像圓形墩柱采用其他參考點建立觀測坐標系。矩形墩柱豎直度檢測示意如圖3，具體步驟如下。

圖3 矩形墩柱豎直度檢測示意圖

2.2.1 數據采集

1)參考點坐標測量：找一個能同時觀測縱、橫橋向面的位置(也可分別兩個方向檢測，本文不做討論)，架設全站儀。在縱橋向面底部利用水平尺標記參考點E1和E2(E1和E2在同一水平面上，任意間距均可)。在同一高度的橫橋向面同樣標記參考點F1和F2。測量E1坐標(x11,y11,z11)、E2坐標(x21,y21,z21)、F1坐標(x12,y12,z12)、F2坐標(x22,y22,z22)。

2)特征點坐標測量：根據墩柱高度在墩身大致均勻位置，檢測若干個能反應墩柱特征的點(底部利用控制點，每面頂部1個測點，中間若干點，各點盡量靠近軸線)，并采用無棱鏡坐標測量模式測量縱橋向面上各點Ei的坐標(xi1,yi1,zi1)和橫橋向面上各點Fi的坐標(xi2,yi2,zi2)。

2.2.2 數據計算分析

橫橋向豎直度計算方法和縱橋向一致，故計算過程以縱橋的豎直度計算為例。

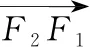
2)計算E1E2鉛垂面方程：E1E2鉛垂面方程為A(X-x11)+B(Y-y11)+C(Z-z11)=0，化簡為：A(X-x11)+B(Y-y11)=0。其中E1的坐標(x11,y11,z11)也可以用E2的坐標(x21,y21,z21)代替參與計算。

3)計算縱橋向面上各點Ei(xi1,yi1,zi1)到E1E2鉛垂面距離di1：

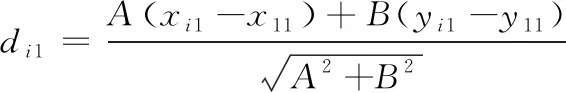
由此計算得E2、E3、……、En各點到E1E2鉛錘面的距離d21(為0)，d31、……、dn1。

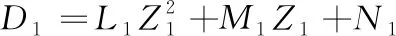
5)計算縱橋向墩柱偏移值：δ1=D1(zn1)-D1(z21)，偏位方向根據計算值的正負判斷。

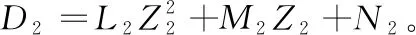
3 工程實例

以某高速公路一匝道立交橋圓柱墩的豎直度檢測為例。墩柱編號為1-0#，直徑1.8 m，高30.8 m。該墩柱臨近懸崖邊，故采用全站儀進行檢測。檢測時以縱橋方向大樁號為X軸正方向，面向大樁號橫橋向左側為Y軸正方向，豎直向上為Z軸正方向建立坐標系。約10 m布置一個檢測斷面，共4個檢測斷面，各特征斷面點坐標檢測數據見表1,表中數據已精確至mm。

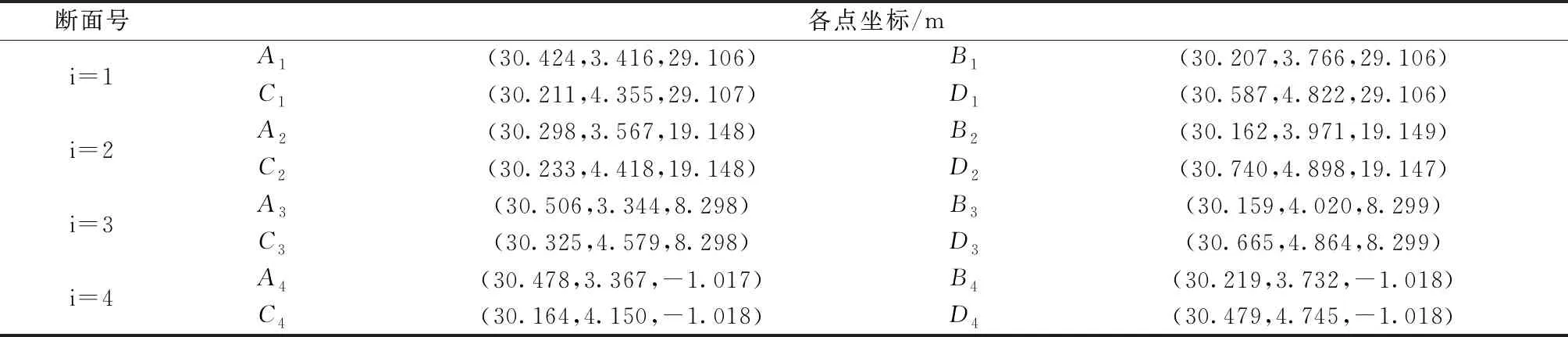
表1 各特征斷面點坐標檢測數據

根據各斷面檢測點Ai、Bi、Ci、Di坐標計算圓心坐標(Xi，Yi，Zi)得：O1(31.063,4.055,29.106)，O2(31.065,4.054,19.148)，O3(31.056,4.056,8.299)，O4(31.062,4.056,-1.018)。

分別對縱、橫橋方向數據采用最小二乘拋物線擬合。擬合出縱橋向變形曲線方程為：X=9.243×10-6Z2-1.342×10-4Z+31.0604(單位:m)；橫橋向變形曲線方程為：Y=2.744×10-6Z2-1.274×10-4Z+4.0561(單位:m)。

故縱橋向偏差為δ1=X(Z1)-X(Z4)=3.8mm，方向為大樁號側；橫橋向偏差為：δ2=Y(Z1)-Y(Z4)=-1.5mm，方向為橫橋向右側。

對于公路橋梁墩柱豎直度檢測結果均按《公路工程質量檢驗評定標準.第一冊.土建工程》(JTG F80/1—20017)中相關的要求評定。以該標準JTG F80/1—20017為例：高度H≤5 m，允許偏差≤5 mm；5 m60 m，允許偏差≤H/3000,且≤30 mm。[3]故1-0#墩柱的允許偏差為20 mm，其縱橋向和橫橋向豎直度均合格。

[ID:010014]