血栓非線性黏度性質研究

高彭松， 李 艷， 剛芹果， 王光磊， 王洪瑞， 王中陽

隨著人們生活水平提高，心腦血管疾病更為多發，成為引發其他各種疾病甚至死亡的常見疾病［1］。血栓是各類心腦血管疾病一大誘因［2］，常見治療方法包括抗凝藥物、手術取栓及系統溶栓。介入技術發展，使得導管直接插入血栓溶栓普遍推廣。然而介入取栓過程中血栓離析和重新凝結會導致患者突然死亡，這與其生物力學特性，尤其是流變學性質有著緊密聯系［3］。近年許多學者對血栓進行研究，主要通過彈性實驗、拉伸實驗評價和比較血栓模型機械力學性能（回復度、最大拉伸長度），實驗設計均從固體力學角度出發，相較于動態分析儀缺乏流變性質表述［4-7］。目前關于血栓流變性質研究相對較少。李元杰等［8］在血液和斑塊等與血栓組織成分或環境相近流變學研究中發現，血栓形成與血液黏度有著緊密聯系，認為血液黏度超過某一臨界值時血栓會首先在管壁附近形成，血黏度低于臨界值時血栓能逐漸化解，以至消失。李志勇［9］同樣研究發現，血管在斑塊生長過程中會逐漸狹窄，斑塊因此處于高剪切環境，但斑塊如何生長成為易損斑塊和斑塊最終如何破裂的生物力學機理尚不清楚。本研究在上述研究基礎上，結合真實數據，分析血栓黏度隨剪切速率變化的關系，并與已知流體黏度模型作對比，選擇出擬合效果更好的模型，同時討論方程模型中的某些參數，以此研究血栓流變行為。

1 材料與方法

1.1 臨床資料與實驗器材

2017年6月至2019年4月，與河北大學附屬醫院介入血管外科醫師合作，獲取8例患者手術取栓后離體1 h真實血栓樣本（圖1）。其中男7例，女1 例，年齡為 51～65 歲，平均（59.2±4.5）歲；發病時間 3～10 h，平均（5.8±2.4） h；病灶部位：左側頸動脈3例、右側頸動脈1例、左側大腦中動脈1例、右側大腦中動脈2例、基底動脈遠端1例。實驗儀器包括MCR301型旋轉式流變儀（奧地利Anton Paar公司）、DC-2006型恒溫水浴箱（上海舜宇恒平科學儀器公司）、BEKO系列空氣壓縮機（德國BEKO公司）；實驗試劑包括無水乙醇、4%甲醛溶液。

圖1 臨床獲取血栓實物

1.2 流變性測試

將血栓樣本從4%甲醛溶液中取出，置于旋轉式流變儀檢測平臺上。選擇直徑為25 mm CP-25錐板作為測試轉子；啟動流變儀和測試程序，設置實驗溫度為37℃，對血栓進行速率-黏度掃描。設定剪切速率變化范圍自1 s-1至100 s-1，取線性變化，每個樣本重復5次實驗，每次實驗間隔30 min，得到血栓黏度隨剪切速率變化的關系。

2 結果

實驗獲得血栓在溫度為37℃時、剪切速率自1 s-1至100 s-1變化下的黏度曲線，不同血栓樣本黏度雖有所差異，但整體變化規律基本一致。以血栓樣本1共5次實驗曲線為例（圖2，為使曲線圖更加清晰直觀，縱軸刻度按照對數規律變化），由圖可知血栓黏度隨剪切速率增加而降低，黏度在剪切速率為10 s-1左右時下降幅度最大，在較高剪切速率范圍內下降趨勢較為緩和，總體表現為剪切變稀的假塑性流體；血栓黏度同時受到實驗次數的影響，隨著實驗次數增加而逐步下降，曲線走勢基本不隨實驗次數增加而變化。Surendra［10］在生物流體力學研究中指出，血液可被認為是冪律流體或Herschel-Bulkley流體；以此為基礎，為進一步描述血栓黏度-剪切速率流變曲線，考慮應用描述假塑性流體黏度的常用模型冪律方程和Herschel-Bulkley方程。

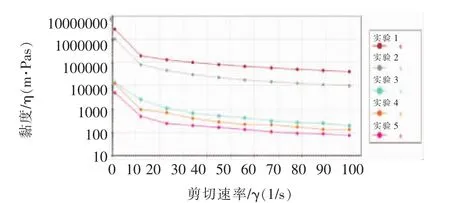
圖2 血栓黏度-剪切速率曲線

2.1 模型選擇

冪律方程是目前在工業領域應用最多的黏度模型方程，其表達式為：

若改寫成應力-剪切速率方程，則為：

式中η為黏度，γ˙為剪切速率，K為黏度指數（K值越大說明樣本黏度越高），τ為剪切應力，n為樣本非牛頓指數。材料為假塑性流體時n＜1，且材料假塑性越強，n偏離1程度越大。在γ˙一定變化范圍內，K和n可視為常數。取每個樣本第1次實驗數據，得到擬合結果見表1。

表1 冪律方程擬合血栓樣本實驗數據所得參數

結合圖2和表1擬合結果，發現冪律方程所得擬合曲線相關系數R2平均值為 0.922 0±0.011，說明擬合度一般（R2值越接近1，擬合效果越好），同時K值偏大，帶來誤差也較大。這種誤差在剪切速率較低范圍內尤為明顯，這是由于冪律方程僅適合描述屈服應力很小且流變行為無依時性的物質［11］，在物質處于很高（趨于無窮）或很低（趨于0）剪切速率時無法較準確地描述其流變性質。若觀察冪律方程的應力-剪切速率本構方程，即公式（2），其應力在極低剪切速率段理論上應趨于0；而實際實驗中可測得血栓在剪切速率趨于0時仍存在較大剪切應力，如表2。由此可認為，血栓流變學黏度性質中存在較大初始屈服應力，同時為了提高擬合精度，考慮應用帶有初始屈服應力參數的Herschel-Bulkley黏度方程進行擬合。

Herschel-Bulkley黏度模型方程基本形式為：

若改寫成應力-剪切速率方程，則為：

式中τ0為初始屈服應力。與冪律方程相比，Herschel-Bulkley方程多了初始屈服應力這一參數，其物理意義為流體僅在受力大于初始屈服應力時才會流動，受力小于初始屈服應力時流體剪切速率為0［12］。單次實驗過程中，初始屈服應力可視為常數，數值大小可取表2中數據，取每個樣本第1次實驗數據，得到擬合結果見表3。對比冪律方程與Herschel-Bulkley方程對同一次實驗擬合結果，可知Herschel-Bulkley方程有著更好的擬合精度，R2平均值為0.997±0.007，本構方程中參數設置也能更好地解釋實驗現象；不同血栓樣本因其內部組成成分不同，初始屈服應力和黏度指數差異較大，兩種方程擬合得出的K值與n值也有一定差異，但總體趨勢相同，可以說明Herschel-Bulkley方程更適合描述血栓的流變行為。

2.2 初始屈服應力分析

Herschel-Bulkley方程中初始屈服應力通常被認為是一定值常數，在部分血栓樣本中數值較大。觀察圖2可發現，血栓黏度會隨實驗次數增加而減小，若對重復實驗數據選用初次測量的初始屈服應力進行擬合，則會導致方程（3）中第1項過大而無法對黏度作準確描述。現定義每個樣本第1次實驗所得初始屈服應力為τ0，后續實驗中初始屈服應力為τ0'。實際上，羅靜等［13］在材料流變學研究中就提出流體初始屈服應力大小會因添加劑多少和溫度高低而改變。由于血栓特殊性，研究其力學行為需要在近似人體體溫環境下進行，血栓組織中也不含添加劑成分。因此，可將后續每次實驗中的τ0'視為隨實驗次數（N）和第一次實驗得到的τ0而變化的函數，即τ0'=（N， τ0）。 圖3為8例血栓樣本分別在5次實驗中初始屈服應力隨實驗次數變化的Matlab擬合曲線。

表2 剪切速率趨于0時不同血栓樣本剪切應力

表3 Herschel-Bulkley方程擬合血栓樣本實驗數據所得參數

圖3 血栓初始屈服應力-實驗次數曲線

8例血栓樣本的τ0'隨實驗次數下降表現出兩種不同趨勢，圖3①中4例樣本第1次實驗得到的τ0雖有一定差別，但數值均較大，意味著樣本本身黏度較大，僅在受到較大應力時才會流動，變化曲線體現出很強的非線性；圖3②中4例樣本τ0均較小，說明樣本本身黏度較小，隨實驗次數變化規律接近于線性。總體上，隨著實驗次數增加，血栓樣本內部流變性質均發生一定程度變化，即使在放置一段時間后也未完全恢復。τ0值大小可在一定程度上反映不同血栓樣本內部成分的差異，影響后續實驗中τ0'隨實驗次數變化的規律。若取初次實驗與末次實驗數據點對曲線作割線，所得割線斜率如下表4。割線斜率反映樣本初始屈服應力隨實驗次數增加的變化速度，可看出8例樣本曲線割線斜率大小基本可劃分為兩種狀況。圖3①中4例樣本τ0均大于500 Pa，割線斜率值較高且相互差值較大；圖3②中4例樣本τ0均小于500 Pa，割線斜率值較低且較為集中，τ0具體數值可參見表2。

表4 血栓初始屈服應力-實驗次數曲線割線斜率

根據現有樣本，可初步以τ0=500 Pa為界限，推測τ0＞500 Pa樣本中不含鈣化成分，變化規律如圖3①，τ0≤500 Pa樣本中含有鈣化成分，變化規律如圖 3②。 對于 τ0較大的血栓樣本，如樣本 1、2、4、7，前2次實驗對血栓流變屬性影響較大，實驗次數＞3后τ0'基本可視為隨實驗次數線性下降。5次試驗后8例樣本τ0'均已接近于0，即黏度也是以極低數值在很小范圍內變化。根據已有樣本實驗數據對兩種不同試驗情況進行擬合，得出τ0'=（N，τ0）函數如下：

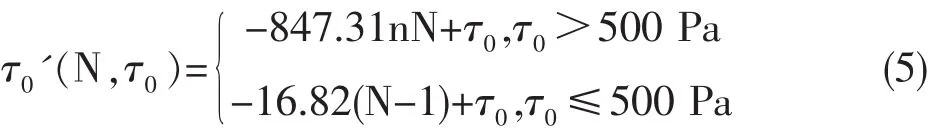
3 討論

為了定量研究血栓流變學黏度特性，本研究應用旋轉式流變儀測定了血栓樣本在不同剪切速率下的黏度數值，并將實驗數據輸入Matlab擬合工具CFtool中，評價與選擇合適的黏度模型對血栓流變行為進行描述。結果發現血栓是典型的剪切變稀的假塑性流體，與冪律方程相比，應用Herschel-Bulkley方程獲得的血栓黏度-剪切速率擬合曲線擬合精度更高，方程中參數τ0設置也更貼合血栓流變學黏度特性。為了更好地解釋重復實驗中血栓樣本黏度下降現象，對Herschel-Bulkley方程中τ0參數又進行討論，分析不同種類血栓初始屈服應力的變化規律，以τ0=500 Pa為指標對血栓種類進行初步劃分，并給出數學模型。該模型能夠為臨床上腔內介入取栓提供一定的生物力學依據。

本研究主要根據真實血栓實驗數據在數值上分析血栓流變學黏性行為，然而對于一些數值差異難以給出準確的基于病理學的解釋。血栓中有無鈣化成分、是否存在炎癥，均會影響其黏度及初始屈服應力，不同患者個體差異性也會導致血栓流變行為有所改變，如何精確建立分類標準還需要積累更多樣本。此外，若按組織成分劃分血栓類型，總體上可分為紅色血栓和白色血栓兩大類，不同血栓類型決定了不同治療措施［14］，如何根據血栓黏度性質確定其內部成分還有待進一步研究。