從某些一元二次方程的另類方法引起的思考

滕曉梅

摘要：從一道中考新題引到應用題的教學環節，通過多種方法的碰撞，體會數學偽生活化的危害。從具體的事例反思數學應用題的教學應該放手讓學生去探討-總結-回顧，進而建模。讓學生充分體會學習的樂趣。

關鍵詞：應用題;建模;偽生活化

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2020）14-106-2

浙江省2011年初中數學學業考試（衢州卷）的21題改編浙教版八年級下冊36頁的例1，這是一道印象深刻的例題，當時在教學這一內容時很還頗讓我苦惱。至今教學片斷還留在我的腦海中。現在把這一例題的教學片斷呈現出來：

一、情境再現，發現問題

1.創設情境

師：方程是刻畫數量關系的典型模型，現在讓我們共同回顧列方程解應用題的基本步驟有哪些？

生1：找數量關系根據數量關系列方程

生2：審題→設元→列方程→解方程→答

師：主要流程不錯，其實大體上分四個步驟：⑴理解問題;⑵制定計劃;⑶執行計劃;⑷回顧。

2.引導探究

師：現在有個實際問題，需要同學們去解決（幻燈片出示例題1）

某花圃用花盆培育某種花苗，經過試驗發現每盆的盈利與每盆的株數構成一定的關系.每盆植入3株時，平均單株盈利3元;以同樣的栽培條件，若每盆增加1株，平均單株盈利就減少0.5元.要使每盆的盈利

達到10元，每盆應該植多少株？

（學生安靜的思考，不一會有幾個學生小聲的討論，些許有些爭論.）

師：問題解決了嗎？

生眾：解決了！

師：下面請一位同學說一下自己的解決辦法.

生1：可以通過列表格的方式來解決，表格如下：

增加（株）123456

盈利（元）10109740

師：（繼續追問）你是怎么想到這個解決方案的？

生1：因為增加的株數是為正整數，而盈利應該是非負數，符合條件的就這幾種，從表格上看只要增加1株或2株就可以了，也就是得出結論每盆應該植入4株或5株。

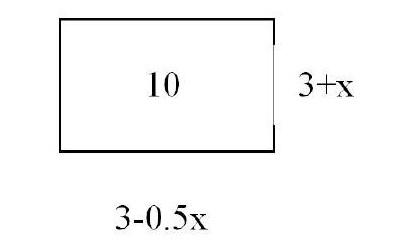
生2：可以把這個題目轉化為已知長方形的面積求邊長的問題

10=1×10=2×5=4×2.5前面的1，2，4代表可以每盆的株數（取整），后面的因數10，5，2.5代表每盆的利潤。根據這個算式可以得出結論每盆應該植入4株或5株。

（課上到這，作為教師的我有點費解，本身不難的題目為什么提問兩個學生還沒得到我滿意的答案，也就是沒有用方程的思想來解決這個題目，我只好再提示，一定要出現我想要的形式為止 。）

師：其實這種方法采用的是數形結合的想法，巧妙地把10分成兩個數之積的樣子，結合題意找出符合條件的答案，其實這個長方形的引入關系不大，還有別的解決方案嗎？可否用設元的方式解決呢？

生3：可以設每盆花苗增加x株，則每盆花苗有（3+x）株，平均單株盈利為（3-0.5x）株，由題意可以列如下方程：（3+x）（3-0.5x）=10解出方程即可。

（終于出現我想要的方法了，稍作總結此類題目的解決方法，匆匆的進入下一個環節講解另外一個例題了。）

二、思考問題，初步診斷

下課之后，再次回想這個教學片段，不禁思考對于此例題學生為什么不喜歡用方程的思想來解決呢？而選擇用列算式的方法去運算。與其說不喜歡還不如說不知如何用列一元二次方程的方法去解決。發現此問題不由得讓我反思起來，按慣例初二的學生已經適應用方程來解決實際問題，已經可以批量化解決題目，這也變成約定俗成的事情了。問題到底出現在哪？

1.我的教學思路

我看到此例題之后建立如下講解思路：

（1）先考慮設直接未知數，即設“每盆植x株”，讓學生通過嘗試發現這樣設未知數對表示相關量不方便，因為題設中和各相關量是“每盆花苗增加”的株數，通過上述啟發，讓學生想到設間接未知數“設每盆花苗增加的株數為x”株。

（2）啟發學生用關于x的代數式表示相關的數量，根據等量關系：平均單株盈利x株數=每盆盈利10元，列出方程。

我自認為這是多么好的啟發式教學呀。其實大多數老師碰到這個題目都會首選這種方法，因為我們已經被“格式化”了，我們已經變成解題機器了。其實我們也希望自己的學生變成解題機器，現在想想對于初二的學生如果老師在平時的教學中沒有充分讓學生體會做題目的樂趣，如何能讓他們堅持到初三的復習，這也許就是大多數老師講的初二的學習將會是個分水嶺的一個原因所在。

2.學生的解決辦法

大部分學生的解法避開方程，而采用枚舉法來解決，教學片斷中予以體現。（還有一些相類似的解法不在此列舉），還有學生用函數的思想來解決，通過畫圖驗證出平均單株盈利是每盆株數的一次函數，由于此法工作量大，就沒在班里介紹。

現在想想為什么不花上一節課真的讓他們開動腦筋把能想到的方法都深入下去，讓他們真正的體會算法多樣化的樂趣，只有在平時把這些落實下去，才能避免初三復習的題海戰，真正的能作到減負于學生，才能更好的應付千變萬化的中考題目。

3.例題的缺點

其實，這個例題老師都清楚，它只不過是披著生活化的外皮實際上是偽生活化的一個題型而已。在教學中學生不領情，這就是原因所在，生活中花農真的是按照這種方式來培育花苗嗎？真的是增加7株，就會單株盈利負0.5元嗎？顯然這不符合生活道理，也無法讓學生理解這個例題的生活化。真的要他們做，他們只能在老師的強制下按部就班的用方程的思想解決此題，其實放手讓他們自己去解決或許有多數人不會用方程來解決，這個題目其實這個題目就是編者編出來的，學生知道老師也知道，現實生活真的會這樣嗎？難道這樣的培育花苗是生活中存在的嗎？這明顯是一道偽生活化的題目，放在這無非是引入一類題型，我們需要這樣的實際問題來充填這部分知識點。 很多知識都要體現從生活中抽象而來，反過來又作用于生活，其實一定要從生活中來確實難為編者了，生活中沒這樣的例子，那就編造一個出來，經過加工提煉或者說是偽造的生活情景，從實際教學的情況來看，學生也根本不感興趣，體現不出數學的應用價值。學生只能體會到這只是做數學題而已，呀. 其實我們老師都清楚這一節課我們就是在傳授一個模型。

總利潤（費用）=總數量×單個利潤（費用）-其它費用

4.例題的復制

有了例1這樣的例題，接著來的就是批量生產出一類練習題，比如本節作業題的第一題，題目如下：某超市銷售一種飲料，平均每天可售出100箱，每箱利潤120元，為了擴大銷售，增加利潤，超市準備適當降價，據測算，若每箱每降價1元，每天可多售出2箱，如果要使銷售飲料獲利14000元，每箱應降價多少元？其實做此類應用題時，要明確題目中所給的信息，并找到其中相等的量可以用不同的表達式表示就可以列出方程。這就是編者編寫它的理由所在，知道本質所在大家都可以編此類題，只不過是冠上不同的生活情景而已，其實都是大家杜撰的生活化，這是出題目的人和做題目的人都心照不宣的事情了。我們老師也要把學生培養成只要看到此類題就可以把模型找出來，進而設元，找等量關系，再列方程解決它。

這類題型的出現把做數學題目當成了零件的批量生產，到了換個馬甲我也認識的地步，其實題目做過之后什么也不會留下，學生就變成了做題目的機器。日以至此，我們的數學變成了什么？數學來源于生活，也必須根植于生活” 。這是每個人教師都會掛在嘴邊的一句話，僅是說說而已嗎？緊密聯系學生的生活實際，讓數學從生活中來，到生活中去，學有應用價值的數學是新課程改革的重要理念。僅是讀讀而已嗎？

三、反思問題，再次診斷

中考題換了一個角度來審視此題，給出學生最熟悉的方法——方程解決此題，要求用一種與之不同的方法求解上述問題。這無疑是給我當頭一棒。敲醒了我，使我對此題有了更深刻認識。基礎知識看似獨立，實際上彼此之間的微妙聯系需要我們老師給學生去總結去提升，我們要在學生現有知識體系下把一張網呈現給學生，引導學生多角度分析一類問題的實質。這樣才能在理性、輕松的學習數學，教師要把基礎知識的來龍去脈多方面的展示給學生。就那此題為例，在講授新課的時候教師要從三方面提煉出此題的解決策略，方法一，列表法（此方法直觀形象體現了未知數的變化過程）;方法二，圖像法（此方法在一次函數的基礎上利用圖像直觀性把兩個變量：株數和單株盈利，體現在直角坐標系，代數問題轉化為幾何問題）;方法三，方程法（解決實際問題需要最簡單的設元法把未知的變換成已知的，借助方程來解決）。其實這里老師還需要一個最優化的講解，以及這三種方法的聯系要引導學生去歸納。這樣也為后續的二次函數打下一個大大的伏筆。我們都相信好的老師只應是引路者而非灌輸者。

（作者單位：浙江省衢州市實驗學校，浙江 衢州 324000）