TI圖形計數器在線性回歸中的應用探究
鄺國均

【摘要】 ?本文主要內容是:通過TI圖形計算器在高中數學線性回歸分析中的應用,展示“TI圖形計算器”其豐富的數學功能,完善的數學設計,不但能夠滿足常規的數學學習和數學教學的需要,而且以其方便于攜帶、操作簡單等特點,為學生提供了一個良好的“玩數學”的環境,成為高中學生手中“流動的數學實驗室”。利用圖形計算器,學生可以隨時隨地的研究數學,讓學生沉浸在“玩數學”的樂趣中。在某種意義上講,TI圖形計算器成為學生手中的一個認知數學的工具,一個了解數學規律的窗口。
【關鍵詞】 ?回歸分析方法 TI圖形計算器 一元線性回歸分析 多元線性回歸分析
【中圖分類號】 ?188 ? ? ? ?? ? ? ? ? 【文獻標識碼】 ?A?【文章編號】 ?1992-7711(2020)21-188-02
0
一、回歸分析方法概述
(1)回歸分析是一種建立統計觀測值之間的數學關系的方法,它通過自變量的變化來解釋因變量的變化,從而由自變量的取值預測因變量的可能值,它是概論、統計學中的重要組成部分。
(2)線性回歸分析方法
包括:一元線性回歸,多元線性回歸。
(3)線性回歸模型的檢驗
判定系數r2——用來判斷線性回歸方程的擬合優度。通常認為當r2大于0.5時,所得到的回歸直線擬合得比較好,而當r2小于0.5時,所得到的線性回歸直線很難說明變量之間的依賴關系。可以說r2越大,函數擬合效果越好。
(4)回歸預測的步驟
第1步,獲得自變量和因變量的觀測值
第2步,繪制X-Y散點圖
第3步,求出含未知參數的回歸方程
第4步,觀測回歸方程的擬合優度
第5步,進行預測
二、一元線性回歸分析
一元線性回歸模型描述的是兩個變量之間的線性相關關系。假設有兩個變量x和y,x為自變量,y為因變量。一元線性回歸模型的基本結構形式為y=a+bx(a和b為待定參數)
例1:為了研究各某個連鎖飲品店季度銷售額與店鋪附近地區居民人數之間的關系,隨機抽取了十個分店的樣本,得到的數據如下:
利用TI圖形計數器的列表與統計功能(Statistics with List Editor)輸入數據和繪制XY散點圖分別得到:圖(1)
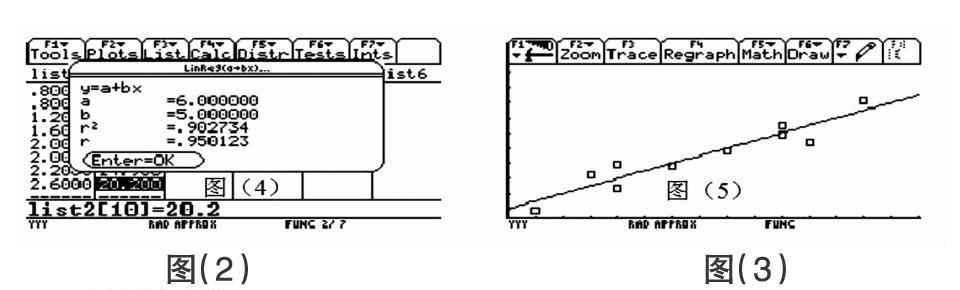
進行函數擬合得到一元線性回歸模型:如圖(2)、圖(3)所示
結果如下:
一元線性回歸模型為:y=6.000000+5.000000x
回歸分析結果為:r=0.950123,r2=0.902734,說明所得到的回歸直線擬合得較好。
預測作用:當我們想要預測區內大學生人數為1.9萬的店鋪的季度銷售額時,只要輸入y2(1.9),如上圖:y2(1.9)=15.500000萬元
對于預測結論的效果如何,可以指導學生與實際結果進行比較,從而修改函數模型,以得到最好的結果。
三、多元線性回歸分析
在多變量的系統中,除了在某兩個變量之間存在著相互作用和影響而發生某種相關外,在若干個(多于兩個)變量之間也存在著相關影響、相互關聯的情況。因此,多元回歸模型更帶有普遍性的意義。假設某一因變量y受k個自變量x1,x2,…,xk的影響,那么,多元線性回歸模型的結構形式為:Y=a+b1X1+b2X2+…+bkXk .
多元線性回歸預測步驟
第1步,獲取備選自變量和因變量的觀測值。
第2步,從備選自變量中選擇合適的自變量。常用方法有:
最優子集法
第3步,確定多元線性回歸方程中的系數,判斷回歸方程的擬合優度。
第4步,根據回歸方程進行預測。
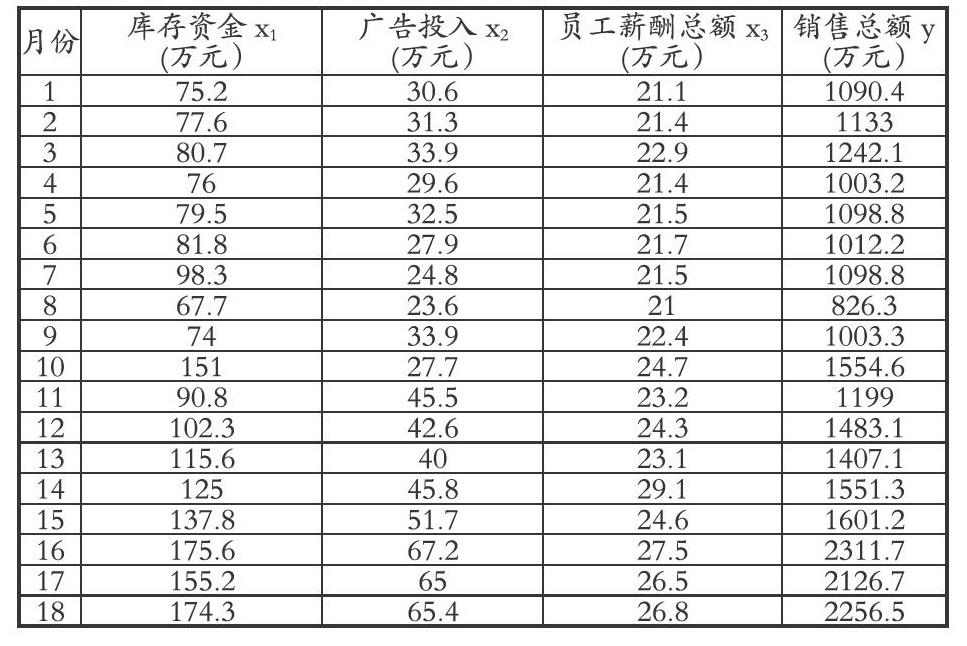
例2:一家服裝零售店將其連續18個月的員工薪酬、庫存占用資金情況、廣告投入的費用、銷售額等方面的數據作了一個匯總表格。該服裝店的管理人員試圖根據這些數據找到銷售額與其它三個變量之間的關系,以便為未來的預算工作提供參考。試根據這些數據建立回歸模型。如果未來某月員工薪酬總額為27萬元,庫存資金額為150萬元,廣告投入預算為45萬元,試根據模擬的回歸模型預測該月的銷售額。采樣數據如下表:
利用TI圖形計數器的列表與統計功能(StatisticswithListEditor)
輸入數據得到:
分別擬合各種變量之間的關系:
①銷售額與庫存資金之間的關系及回歸方程的擬合優度(此時,r2=0.890573)
②銷售額與廣告投入之間的關系及回歸方程的擬合優度(此時,r2=0.837430)
③銷售額與員工薪酬之間的關系及回歸方程的擬合優度(此時,r2=0.709632)
④銷售額與庫存資金、廣告投入之間的關系及回歸方程的擬合優度(此時,r2=0.9577330)
⑤銷售額與廣告投入、員工薪酬之間的關系及回歸方程的擬合優度(此時,r2=0.869615)
⑥銷售額與庫存資金、員工薪酬之間的關系及回歸方程的擬合優度(此時,r2=0.898492)
⑦銷售額與庫存資金、廣告投入、員工薪酬之間的關系及方程的擬合優度(此時,r2=0.957480)
由于④與⑦的擬合后的回歸方程中的R2都很接近,為了從中得到最好的擬合效果,我們再對④與⑦分別進行多元線性回歸分析:
采用最優子集法作為備選自變量篩選
分析比較結果表明:雖然④與⑦的回歸分析中的R2≈0.957,但④的AdjR2(調整后的R2)比⑦的大,所以庫存資金和廣告費用為自變量的多元線性回歸方程效果最好。此時,回歸方程為:
y=86.953190+7.108925X1+13.683731X2(其中,X1,X2分別為庫存資金和廣告費用)
預測作用:未來某月員工薪酬總額為27萬元,庫存資金額為150萬元,廣告投入預算為45萬元,試根據建立的回歸模型預測該月的銷售額為:
y=86.953190+7.108925×150+13.683731×45≈1769.059835萬元
在數學學習活動中,以問題為載體,通過解決實際問題,既培養了學生應用數學的意識,同時也通過在實踐的學習過程中,培養了學生的創新意識和實踐能力。學生通過實際問題的分析,利用圖形計算器,自己動手,進行抽象,簡化,發現數學規律,建立數學模型,從而獲得實際問題的解決,在這一過程中,離不開現代信息技術對數據的處理和分析。TI圖形計算器由始至終作為學生學習的一個學習工具,參與了解決問題的各個階段,幫助學生以數學的方式去理解周圍的世界。
[ 參 ?考 ?文 ?獻 ]
[1]徐勇,高建彪.借助圖形計算器CAS功能解高考題[J].中國數學教育(高中版),2012(11):39-44.
[2]徐勇,高建彪.一例教材中的函數模型擬合之路的探索[J].中國數學教育(高中版),2014(11):56-58.
[3]章建躍.理解數學理解學生理解教學[J].中國數學教育(高中版),2010(12):3-7,15.

