基于多維壓縮感知的雷達(dá)成像方法研究

于 歡, 王鳳姣, 李乃星, 胡 鑫, 周起華

(上海無線電設(shè)備研究所,上海201109)

0 引言

雷達(dá)的回波信號包含目標(biāo)距離、方位和俯仰三個維度的信息。傳統(tǒng)的成像雷達(dá)獲得的目標(biāo)圖像實際上是其三維結(jié)構(gòu)在距離-多普勒平面上的投影。當(dāng)雷達(dá)與目標(biāo)存在相對運動時,目標(biāo)在該平面上的投影也會相應(yīng)發(fā)生變化,成像結(jié)果反映了目標(biāo)的一維方位和俯仰信息。而從雷達(dá)三維成像結(jié)果中可以獲取目標(biāo)三個維度的信息,從而更直觀地對目標(biāo)進(jìn)行描述。壓縮感知理論可以代替匹配濾波實現(xiàn)脈沖壓縮,降低雷達(dá)系統(tǒng)設(shè)計的復(fù)雜度。本文建立了一種基于多維壓縮感知的雷達(dá)成像模型,并針對雷達(dá)回波信號稀疏度未知影響信號重構(gòu)精度的問題,提出了改進(jìn)的分段正交匹配追蹤算法,實現(xiàn)雷達(dá)壓縮感知三維成像。

1 基于壓縮感知的雷達(dá)成像模型

1.1 多維壓縮感知模型

壓縮感知理論[1]基于信號的稀疏性以及線性規(guī)劃,旨在降低信號的采樣頻率,重構(gòu)出高分辨率的信號。壓縮感知主要包括信號的稀疏表示、信號的測量以及信號的重構(gòu)三個部分,如圖1所示。

圖1 壓縮感知理論框架

假設(shè)原始信號X是有限長的離散信號,且X∈C C N,在ψ變換域上能夠稀疏表示為

式中:ψ是N×N的稀疏矩陣;S是一個N×1的矩陣,滿足‖S‖0=K?N,‖S‖0表示矩陣S中的非零元素個數(shù)。將信號X稀疏后,通過非相關(guān)測量將信號X投影到維數(shù)更低的矩陣φ上去,即

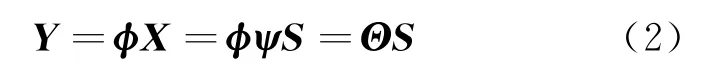
式中:Y是一個M×1(M＜N)的矩陣;φ∈CCM×N,表示測量矩陣;Θ∈CCM×N,表示觀測矩陣。式(2)可以轉(zhuǎn)化為最小l0范數(shù)問題求解,即

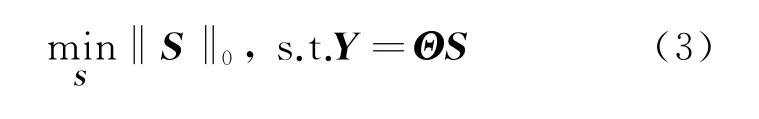
多維壓縮感知模型[2]是在二維壓縮感知模型[3]以及多維矢量矩陣[4-5]理論的基礎(chǔ)上推導(dǎo)得到的。假設(shè)多維信號X在ψ變換域上是稀疏的,將多維矩陣XK1×K2×…×Kr的維數(shù)分成兩組,用矢量I、J表示,其中I=(K1,K2,…,Km),J=(Km+1,Km+2,…,Kr),X表示為多維矢量矩陣XIJ。XIJ在ψ變換域上能夠稀疏表示為

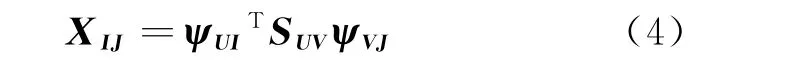
式中:ψUI、ψVJ表示多維矢量稀疏矩陣,多維矩陣ψ的維數(shù)分別按矢量U、I以及V、J分成兩組,其中U=(K1,K2,…,Kn),V=(Kn+1,Kn+2,…,Kr);SUV是稀疏后的矩陣。XIJ經(jīng)過非相關(guān)測量得到測量結(jié)果為

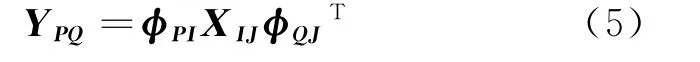
式中:YPQ是多維矢量測量值;φPI、φQJ表示多維矢量測量矩陣;多維矩陣φ的維度分別按矢量P、I以及Q、J分成兩組,其中P=(K1,K2,…,Kl),Q=(Kl+1,Kl+2,…,Kr)。由多維測量值YPQ實現(xiàn)信號的重構(gòu),可總結(jié)為下列優(yōu)化問題,即

根據(jù)上述內(nèi)容可得到三維壓縮感知模型。假設(shè)存在三維信號X∈CCN×N×N,可表示為三維矢量矩陣。其稀疏變換矩陣分別為,記為ψ1和ψ2。信號測量時測量矩陣分別為,記為φ1和φ2。則重構(gòu)三維信號X∈CCN×N×N的問題可表示為

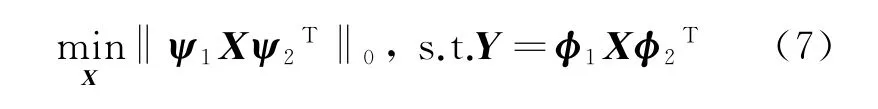
根據(jù)矩陣?yán)边\算可得到Vec(S)以及Vec(Y),進(jìn)一步可得到

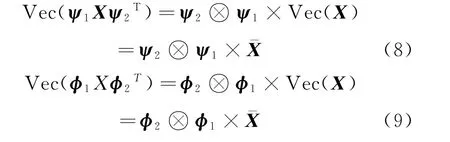
式中:?表示兩個矩陣之間的Kronecker積。因此,三維壓縮感知模型下的優(yōu)化問題可表示為

最后通過貪婪算法等重構(gòu)算法得到三維信號。

1.2 雷達(dá)成像幾何模型

由于多發(fā)多收(Multiple Input Multiple Output,MIMO)雷達(dá)的收發(fā)陣列是面陣,可同時發(fā)射并接收多個相互獨立且正交的信號,因此MIMO雷達(dá)可以獲取更多的目標(biāo)信息。

本文中采用一種收發(fā)陣列為面陣的M2發(fā)N2收的MIMO雷達(dá)[6]。假設(shè)收發(fā)面陣在xoy平面上,發(fā)射陣元及接收陣元的間距分別為dt、dr,滿足dt=(M-1)Nd,dr=2d,其中陣元間距為d。稀疏陣面可等效成(MN)2個收發(fā)共用陣元的均勻正方形陣列,如圖2所示。φ和θ分別表示目標(biāo)相對于收發(fā)陣元的俯仰角和方位角。

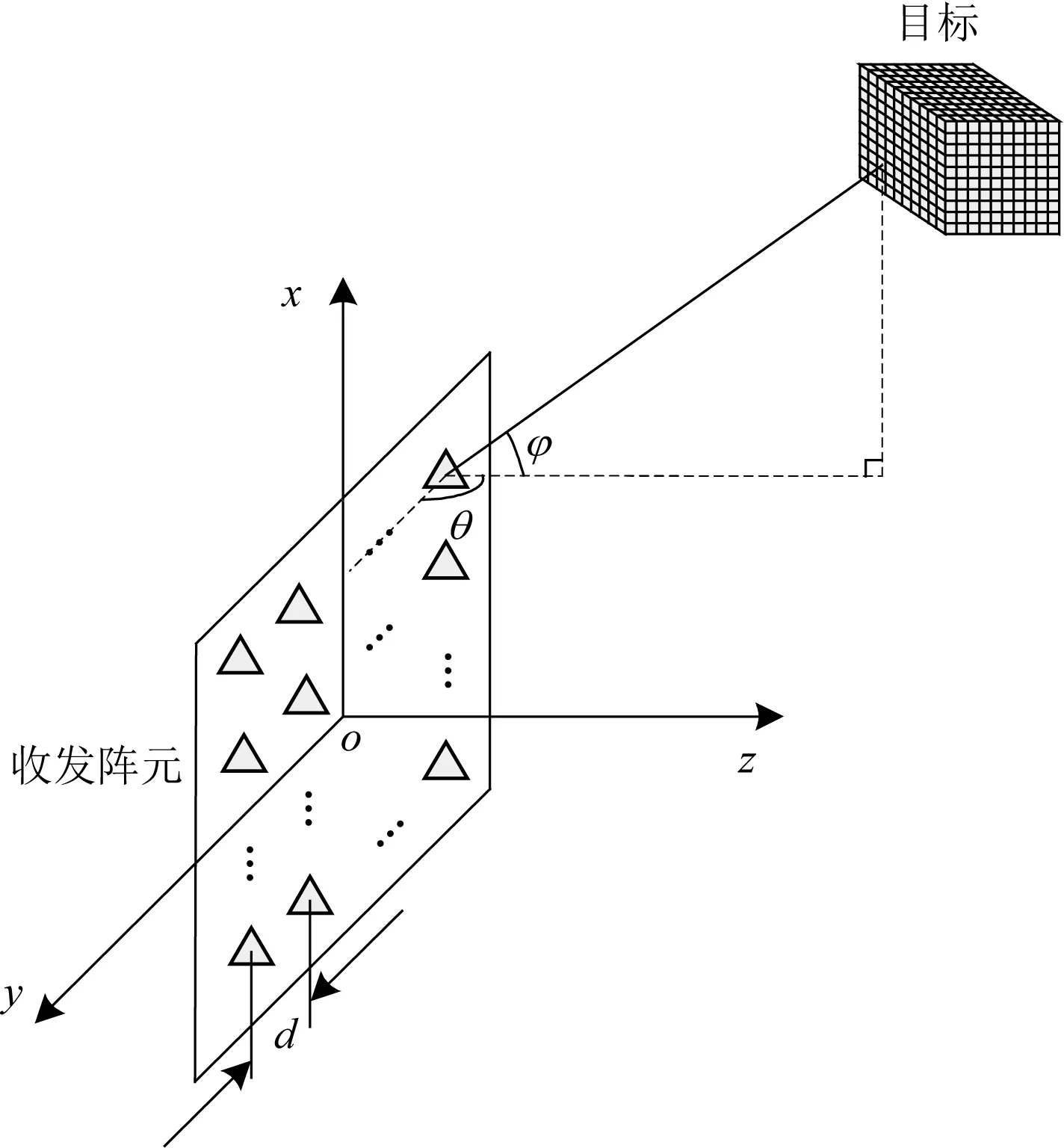
圖2 基于多維壓縮感知的雷達(dá)成像系統(tǒng)幾何模型

1.3 雷達(dá)成像信號模型

第m個發(fā)射陣元發(fā)射的信號sm可表示為

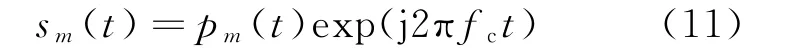
式中:pm(t)是第m個發(fā)射陣元發(fā)射信號的復(fù)包絡(luò);fc是載波頻率。經(jīng)K個目標(biāo)點散射,第n個接收陣元接收到的信號可表示為

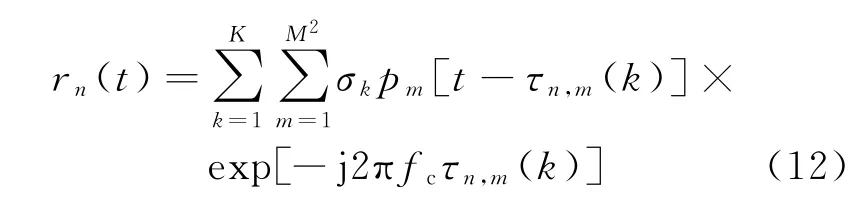
式中:K表示目標(biāo)所劃分的網(wǎng)格點總個數(shù);σk表示第k個目標(biāo)點的散射系數(shù);τn,m(k)表示第m個發(fā)射陣元發(fā)射,第n個接收陣元接收第k個目標(biāo)點反射信號的時延。以Q個采樣頻點對空間頻譜均勻采樣,接收信號在去載波以及時延處理后可表示為

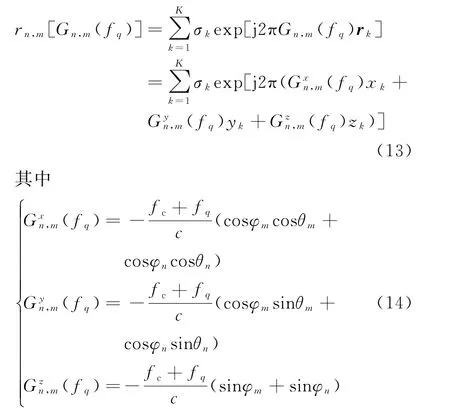
式中:Gn,m(fq)表示第m個發(fā)射陣元發(fā)射,第n個接收陣元接收的信號,在第q個頻點采樣時的空間頻譜;fq=Bq/Q,表示第q個采樣頻點,B為信號的帶寬;rk表示坐標(biāo)原點到第k個目標(biāo)點的向量,可由該目標(biāo)點的坐標(biāo)(xk,yk,zk)表示;分別表示Gn,m(fq)在x、y、z三個維度的單位頻譜;φn和θn分別為目標(biāo)相對于第n個接收陣元的俯仰角和方位角;φm和θm分別為目標(biāo)相對于第m個發(fā)射陣元的俯仰角和方位角。

根據(jù)上文所述,可以構(gòu)造第k個目標(biāo)點的三維回波信號模型,即

其中

式中:Rk∈CCM2N2Q×1;φk∈CCM2N2Q×1,為測量矩陣;φn,m(k)表示在第m個發(fā)射陣元發(fā)射第n個接收陣元接收第k個目標(biāo)點的測量矩陣;e∈CCM2N2Q×1,為加性零均值高斯白噪聲。根據(jù)式(16)、式(17)可得到

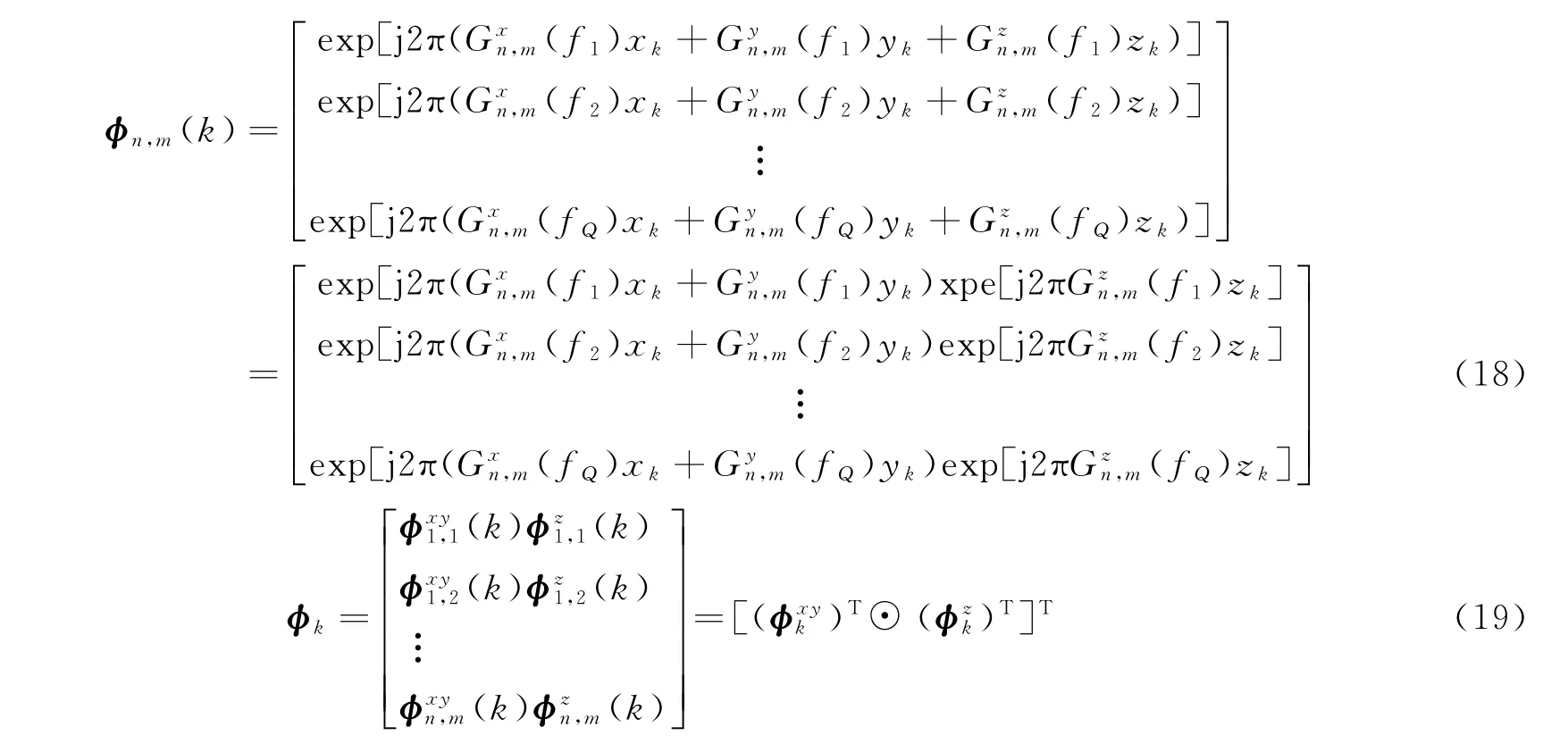
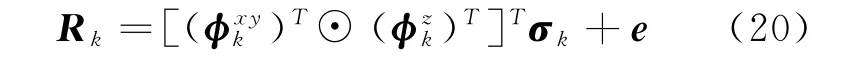
K-R積和Kronecker積可表示為

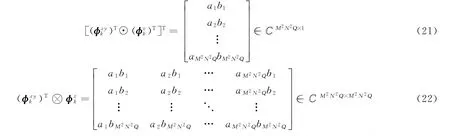
式中:a=[a1,a2,…,aM2N2Q]和b=[b1,b2,…,bM2N2Q]分別為的行矢量。根據(jù)上述兩種乘積的性質(zhì)將第k個目標(biāo)點的三維信號模型轉(zhuǎn)換為

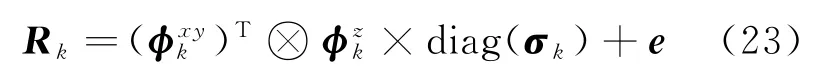
式中:diag(·)表示由括號內(nèi)矢量構(gòu)成的對角矩陣。

2 改進(jìn)的分段正交匹配追蹤算法

分段正交匹配追蹤(Stagewise Orthogonal Matching Prusuit,St OMP)算法[7]相較于正交匹配追蹤(OMP)算法[8]不再是每次迭代過程中選取一個最佳的原子,而是根據(jù)預(yù)先設(shè)定的閾值范圍選取多個原子,從而減少迭代次數(shù)。

StOMP算法的步驟[9]如下:

a)輸入觀測矩陣Θ,測量矩陣φ,稀疏矩陣ψ,觀測向量Y,迭代次數(shù)t,終止最大迭代次數(shù)T,每次迭代索引(列序號)J,t次迭代索引(列序號)集合Λt;

b)初始化,t=1,殘差r0=Y,信號支撐集Λ0=?,J=?;

c)計算向量內(nèi)積u(j)=〈rt-1,Θj〉,其中Θj為Θ的第j列,且1≤j≤N;

d)根據(jù)閾值,將選取的索引值放到信號支撐集中。令δt為噪聲系數(shù),gt為閾值參數(shù),則J={j:u(j)≥δtgt},Λt=Λt-1∪J;

g)t=t+1,如果t＜T則返回步驟(c)繼續(xù)迭代,直至t=T;

傳統(tǒng)的St OMP算法存在以下兩個缺點:

a)無法確定重構(gòu)信號的稀疏度;

b)重構(gòu)結(jié)果依賴于終止條件,錯誤原子的引入造成重構(gòu)精度的降低,即在St OMP算法的迭代過程引入錯誤的索引值(列序號)。

結(jié)合稀疏度自適應(yīng)思想[10],在兩種改進(jìn)的信號稀疏求解算法[11-12]的基礎(chǔ)上提出一種針對本文中三維信號模型的改進(jìn)的St OMP算法。

改進(jìn)的St OMP算法的步驟如下:

a)輸入觀測矩陣Θ,測量矩陣φ,稀疏矩陣ψ,觀測向量Y,步長l,迭代次數(shù)t,迭代階段tstage;

b)初始化,t=1,殘差r0=Y,信號支撐集Λ0=?,J=?,l=ls;

c)計算向量內(nèi)積u(j)=〈rt-1,Θj〉,其中Θj為Θ的第j列,且1≤j≤N,J={j:u(j)≥δtgt};

d)再選取u中l(wèi)個最大值,設(shè)其對應(yīng)的列序號j的集合為H,Λt=Λt-1∪J∪H;

f)在中選取絕對值最大的l項記為,其對應(yīng)的列序號集合為F=ΛtL;

h)若‖rt‖2＞‖rt-1‖2時,則停止迭代進(jìn)入步驟(i);若‖rt‖2＜‖rt-1‖2時,則t=t+1,Λt=F,進(jìn)入步驟(c);若‖rt‖2=‖rt-1‖2時,則tstage=tstage+1,l=tstage×l,Λt=F,進(jìn)入步驟(c);

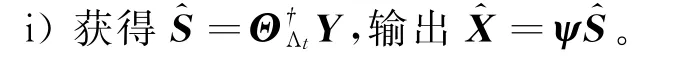
3 仿真結(jié)果與分析

為驗證改進(jìn)的St OMP算法對三維雷達(dá)信號的重構(gòu)效果,利用MATLAB進(jìn)行仿真實驗。假設(shè)圖2雷達(dá)成像系統(tǒng)幾何模型中,收發(fā)天線陣列分布在xoy平面上,中心位置位于空間直角坐標(biāo)系的坐標(biāo)原點。雷達(dá)發(fā)射陣元個數(shù)M2=9,接收陣元個數(shù)N2=64,發(fā)射陣元間距dt=16 m,接收陣元間距dr=2 m,可以等效成收發(fā)陣元間距為d=1m的24×24個收發(fā)共用陣元的均勻正方形陣列。信號載波頻率fc=10 GHz,帶寬B=50MHz,采樣次數(shù)Q=20,對成像區(qū)域內(nèi)的10個目標(biāo)點進(jìn)行成像,成像區(qū)域大小為10 m×10 m×10 m。重構(gòu)結(jié)果如圖3所示。

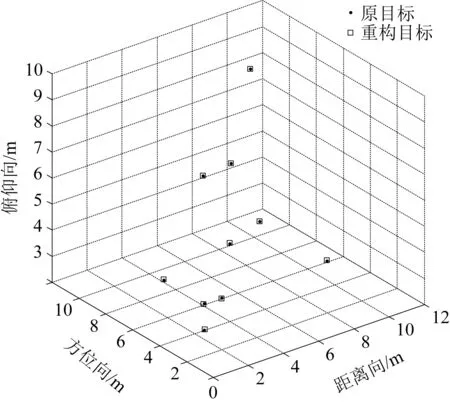
圖3 三維雷達(dá)信號目標(biāo)重構(gòu)結(jié)果

由圖3可知,改進(jìn)的St OMP算法可以將目標(biāo)點準(zhǔn)確地重構(gòu)出來,并保留目標(biāo)點的俯仰信息、方位信息以及距離信息。用成像誤差,即成像均方根誤差(Root Mean Square Error,RMSE),表示成像結(jié)果與原目標(biāo)位置偏離程度,表達(dá)式為

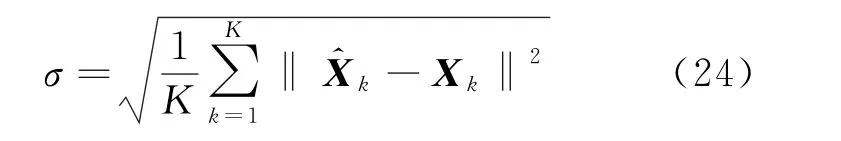
本文所提出的改進(jìn)的St OMP算法與OMP算法、St OMP算法重構(gòu)效果的對比結(jié)果如圖4所示。由圖4(a)可以看出,相同稀疏度條件下,改進(jìn)的St OMP算法的信號重構(gòu)成功概率要高于OMP算法以及St OMP算法;由圖4(b)可以看出,同樣信噪比條件下,采用改進(jìn)的St OMP算法的成像誤差小于OMP算法以及St OMP算法,成像質(zhì)量更高。

4 結(jié)論

本文推導(dǎo)出一種基于多維壓縮感知理論的雷達(dá)三維信號模型,并研究得到一種適用于該信號模型的改進(jìn)的St OMP算法,用于進(jìn)行信號重構(gòu)。研究表明:在本文所提出的雷達(dá)三維模型基礎(chǔ)上,改進(jìn)的St OMP算法克服重構(gòu)信號稀疏度未知,以及重構(gòu)過程中結(jié)束條件導(dǎo)致錯誤原子引入的缺點,提高了信號的重構(gòu)效果,完整地保留了目標(biāo)點的俯仰向、方位向以及距離向三個維度的信息。

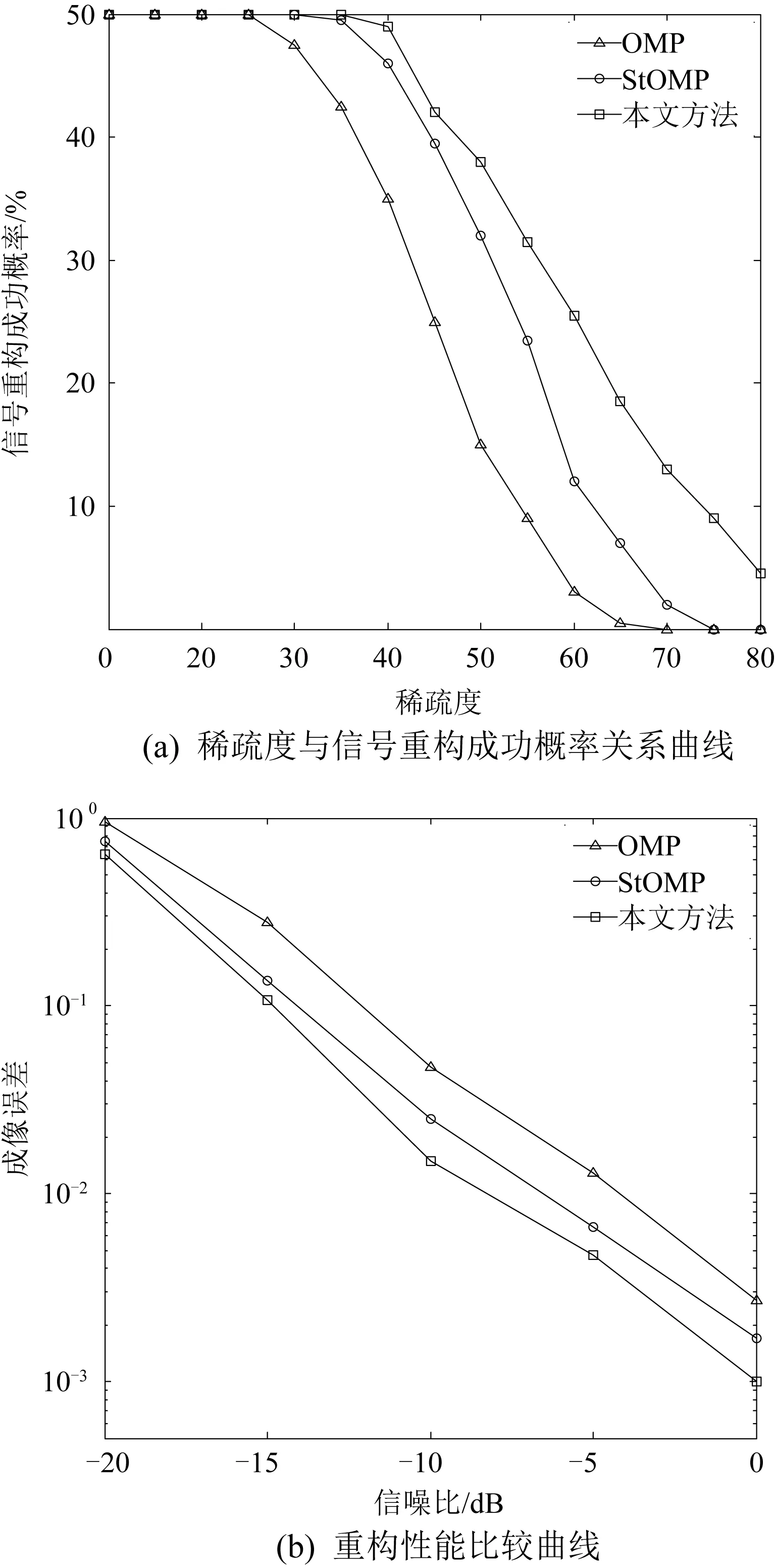
圖4 改進(jìn)St OMP算法與其他算法重構(gòu)效果對比圖