主成分回歸模型下智能農機對耕深的影響研究
趙嘉琦 高阿芳 閆新洋 曾繁湫 李思源
(1.長春工業大學數學與統計學院,吉林 長春 130012)
1 研究設計
1.1 數據選取
本文所用數據為吉林省長春市試驗農田采集的真實有效數據。
1.2 方法選取
農田采集的數據各變量相互關聯,量化分析可以避免數據之間存在復雜的共線性。主成分回歸模型先對主成分進行分析,選取代表性的指標替代原有指標,并反映原指標較為全面的信息,且結果準確無誤,具有典型性。
1.3 指標選取
國內外各研究者對農業研究的指標選取有所差異,通過資料的查詢及農田實地的考察,選取異于常人的指標進行研究,如下表1為本文所選取的幾個指標。
1.4 方法說明
1.4.1 主成分
主成分分析是變量相關關系的一種多元統計方法,其步驟為:選擇最初研究指標;求其特征根與特征向量;查看kappa值,若大于100,先消除共線,再進行下一步操作;通過碎石圖選取主成分個數,為進一步確定準確的主成分個數,查看特征值及累積貢獻率,若累積貢獻率大于80%,則選取前面相對應的指標;獲取的結果結合實際情況進行分析。
1.4.2 主成分回歸模型
(1)模型。
Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+μ
(2)回歸分析。
運用Python、R軟件錄入數據,先進行主成分分析,將獲得的主成分綜合加權并采用逆變換法,得到原始變量的綜合關系式。
2 實證分析
2.1 相關矩陣
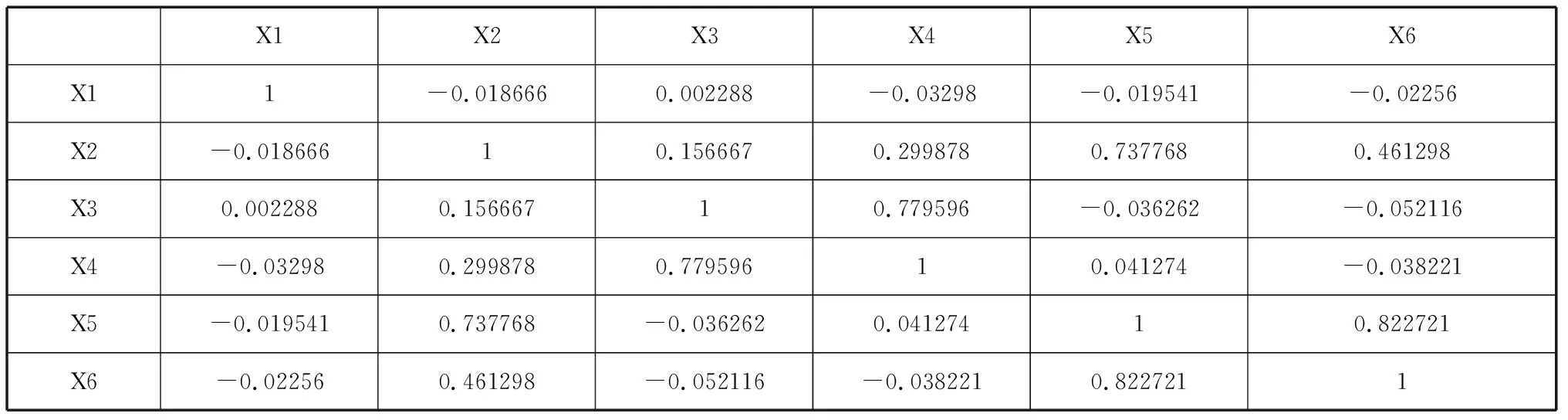
表2 相關矩陣
由上表2,指標間的相關系數矩陣數值可以看出變量間具有相關關系。為了降低數據維度,我們對指標進行因子提取,雖然這些指標之間的單位相同,但為了后文數據的一致性,對其進行標準化處理,并進行因子分析。
2.2 碎石圖
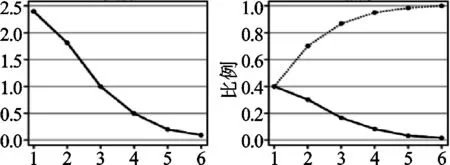
圖1 碎石圖
從圖1中可以看出前3個主成分的提取對原變量信息的刻畫有顯著作用,為此我們抽取3個固定的因子數量,并得到下表。
由表3可知,前3個主成分X1、X2、X3的累積貢獻率為86.84%,大于80%。因此,對第三主成分以后的主成分完全可以忽略不計,即取前3個為主成分代替原來的六個指標,起到了降維的作用。
2.3 特征值及累積貢獻率

表3 特征值及累積貢獻率
2.4 主成分得分

表4 主成分得分
求主成分的因子載荷矩陣,確定主成分與變量間的表對載荷矩陣的第i列的每個元素分別除以第i個特征根的平方根,就得到主成分分析的第 i個主成分的系數,由此得到前3個主成分X1、X2、X3的線性組合為(X為標準化后的變量)。把系數和相應的指標相乘后再求和,可以得到最終的主成分的分公式:
F1=-0.287X1+0.550X2+0.137X3+0.198X4+0.602X5+0.526X6
F2=-0.014X1+0.051X2+0.672X3+0.665VBX4-0.202X5-0.249X6
F3=0.999X1+0.022X2+0.033X3-0.006X4+0.017X5+0.006X6
本文僅從單純的數量上考慮,以3個因子的方差貢獻率為權數。即:P=0.4F1+0.3F2+0.17F3
2.5 回歸模型
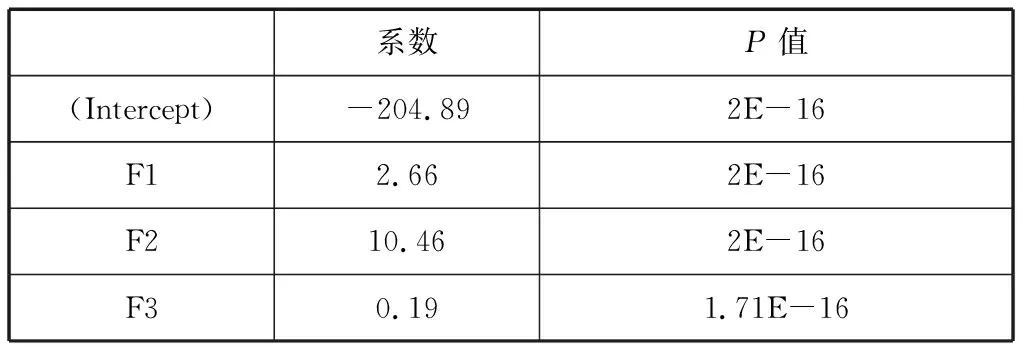
表5 主成分回歸
對具有代表性的主成分進行回歸分析,從上表5中可以看出F1、F2、F3的P值均小于0.05,且調整后的R2為0.988,得出3個主成分可以表達98.88%的信息,其效果顯著,F1、F2、F3的回歸關系式為:Y=204.89+2.66F1+10.46F2+0.19F3
采用逆變換法,運用代碼求原回歸模型,最終求得回歸方程為:Y=226.43+55.47X1-0.85X2-8.65X3-7.53X4+0.27X5+0.54X6
3 結語
本文通過主成分回歸分析得出,左下拉桿鉸接點、左下拉桿傾角、右下拉桿傾角與耕深成正比例,右下拉桿鉸接點、左下拉桿、右下拉桿與耕深成反比例。在農田地表溫度、酸堿度特定的條件下,耕深的深度決定糧食的產量。因此,在未來的農田耕種中,可以通過給定的變量值不斷試驗耕深,以求達到糧食產量的增加。

