初中數學探究性命題的類型與解題方法芻論
林艷玉
(福建省漳州市華安縣第一中學 363800)
初中數學作為進一步提升學生數學基礎、開啟學生邏輯思維及發展性思維綜合能力的階段,對學生今后的學習有著更加重要的影響.因此,傳統的教學模式已經不能夠滿足新時期初中生的發展需求.要想進一步夯實學生的初中基礎知識,就要根據現階段學生的實際情況出發,積極轉變教學主體,以更加靈活的引導方式,來提升學生對基礎知識靈活應用的能力,這對學生的長遠發展會奠定更加有力的基礎.
一、關于探究性命題類型的論述
關于探究性題目的具體概念,目前并無具體明確給定.但在一般情況下,探究性題目具有一定的開放性以及不固定性.因此,該類型題目可以為學生的獨立思考與學習提供更加寬松的空間,同時對學生的各項思維能力也具有一定的培養作用,并通過不同方式的解題思路,能夠讓學生掌握更多的解題技巧.
1.從結論中給出條件
滿足結論的條件并不是唯一的,是對學生探索、分析及反思能力的一種考驗,具有一定的開放性特點.
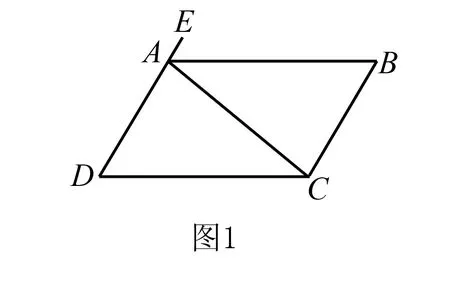
例1圖1,如果想要得到AB∥DC,只需要滿足何種條件.
該類型題目就是通過給出一定結果及條件,來分析相應的對象是否存在.該種答案有不存在和存在兩種情況,因此主要的解題方法,就是通過演繹、推理、假設存在而得出結論,同時對題目做出準確有效的判斷.比如要想證明AB∥DC,只需要找出內角角度以及其余兩邊是否平行,證明角與線之間的關系,即可做出準確解答.
2.結論開放型題目
3.簡單開放型題目
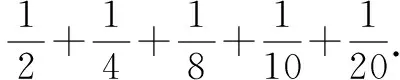
學生根據所學知識以及思維能力,可能會得出以下結論.
其一:直接通過通分方式進行相加減,然后再通過約分而得出正確結論:
其二:通過最小公倍數,來得出最后答案:
對于這兩種解題思路來說,方法一主要是通過常規的計算方式,讓分母統一,從而進行分子的相加減;而方法二更加體現了一種化歸思想,雖然同樣使用最小公倍數,但該種方法相對來說更為簡便.
二、關于探究性命題方法的論述
1.靈活運用輔助線來提升論證能力
該類型題目是以幾何圖形作為題目背景的,通過設置相應的點與線,從而建立圖形關系.
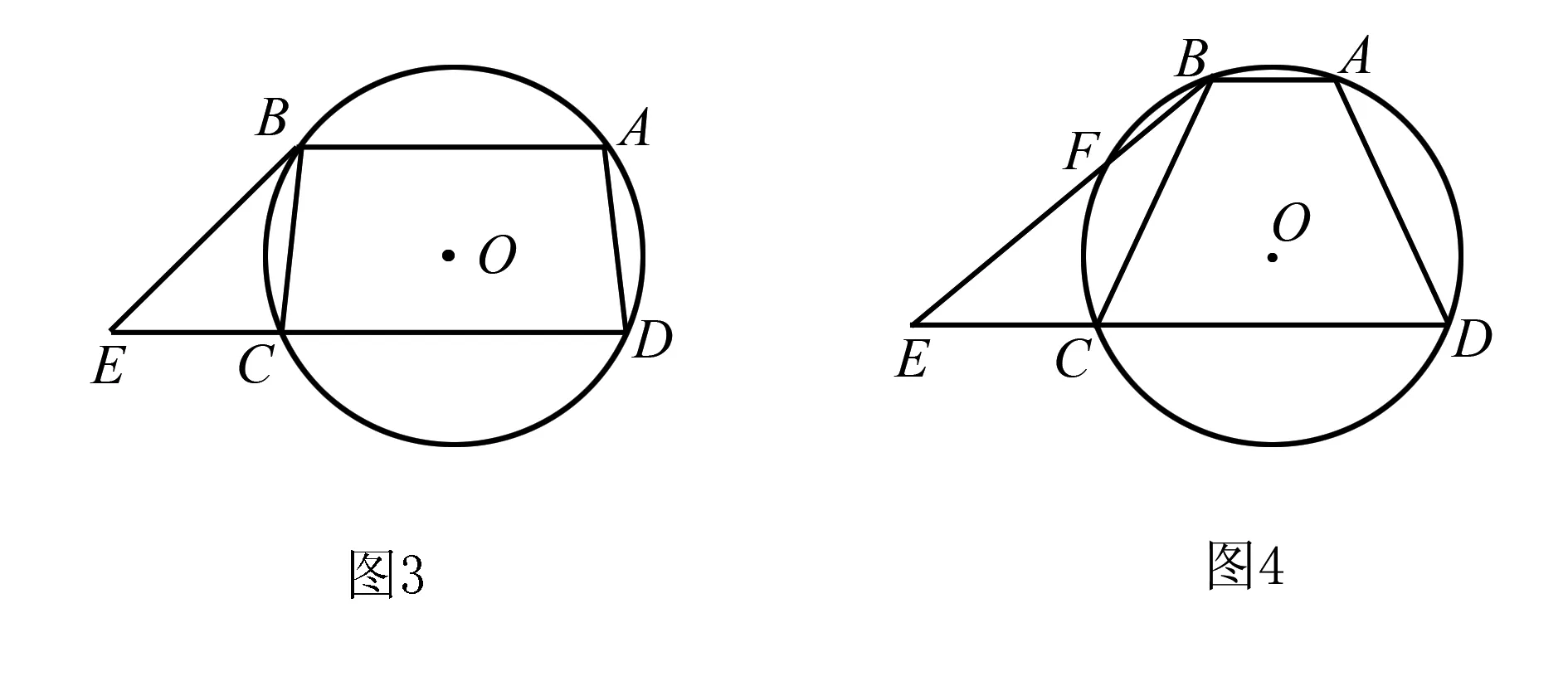
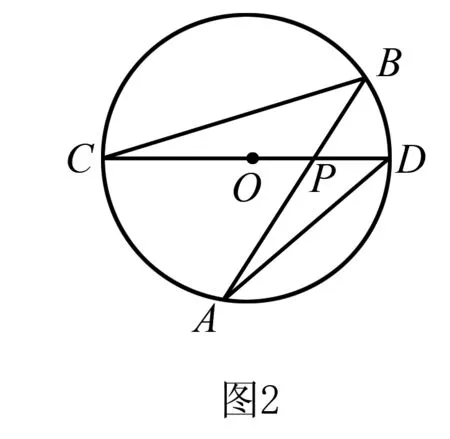
例4 如圖3所示,四邊形ABCD是⊙O的內接四邊形,B是弧AC的中點,過B點的切線與DC的延長線交于點E.根據圖形所示,(1)證明:BC·AB=AD·CE;(2)如圖4,如果點E在CD的延長線上運動,點B在弧CD上運動,使切線EB變為割線EFB,其他任何條件依舊,那么需要具備什么樣的條件,可以使原有結論成立.(注:只要求畫出示意圖注明條件,無需證明)
該類型題目是一道典型的條件探索問題,因此要以“執果索因”的方式進行解答論證.要想求證BC·AB=AD·CE,就要論證出△BCE∽△DAB,通過已給出的條件∠BCE=∠BAD外,還需要尋找更多條件,如∠CBE=∠BDA,來進行有效證明.
2.靈活運用基本知識尋求更多思路
學生思路的打開條件,是建立在對知識牢固掌握的基礎上,這樣可以使其發散思維及邏輯思維能力增強.因此,有效掌握基礎知識,同時加強開放式習題的練習,可以不斷突破學生的思維局限,有效提升學生靈活思考及分析能力.
例5 在一個多項式如16x2+1中,添加一個單項式,讓其變為完全平方式,那么添加的單項式應該是什么?
分析如果要想使多項式16x2+1成為完全平方式,可以添加常數項,也可以添加二次項.
解答如添加8x,即可變成(4x+1)2;如添加-8x,即可變成(4x-1)2;如添加-1時,即可變成(4x)2;如添加-16x2,即可變成12.
例6 如圖5所示,現已知△ABC內接于⊙O,CB為圓的直徑,過點C作直線EF,要想使EF成為⊙O的切線,那么需要添加哪種條件?
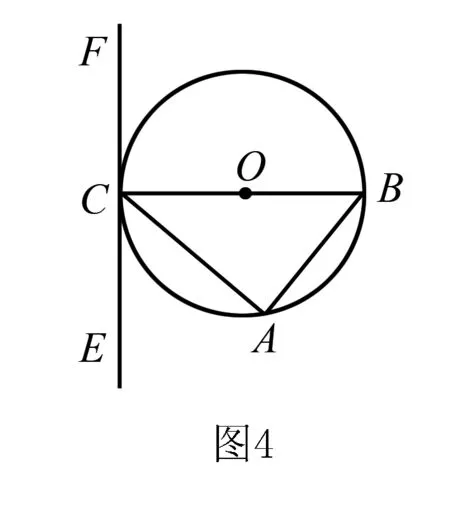
分析題目中已給出所需條件,因此又想EF成為⊙O的切線,分析出關鍵是CB⊥EF這個條件是否成立,如果成立即可證明.
解答條件為∠ACE=∠ABC、CB⊥EF、∠CAB=∠FCB、∠BCA+∠ACE=90°、∠ECB=∠BCF.
探究性題目具有更多的生動性、多樣性及靈活性,以開放的形式及無固定模式的解題思路,來考驗學生的思維能力、對基礎知識的掌握能力及靈活應用能力,使學生通過該類型題目,能夠提高其歸納、分析、想象、觀察、類比、概括等綜合思維方式,對提升學生整體的數學素養提供了更加有力的條件.

