高等職業教育規模與區域經濟耦合協同發展研究

葉沖

摘 要 為探討高等職業教育規模與區域經濟的內在聯系，基于我國西部12省（市、自治區）2008-2017年的面板數據，在構建評價指標體系的基礎上，運用熵值法、綜合評價模型、耦合協調度模型和灰色預測模型，對高等職業教育規模和區域經濟的耦合協調程度的時序演變進行分析。研究結果表明：西部地區高等職業教育規模系統與區域經濟系統的發展水平均呈上升態勢，且高等職業教育規模系統的綜合評價指數明顯高于區域經濟系統;兩大系統的耦合度較高，但耦合協調度不高，才跨入初級耦合協調水平;省際間跨越等級不同，均未達到優質協調等級。未來五年，西部地區的耦合協調度將穩步提升，各省協調發展演進速度差異明顯。因此，需要深化高等職業教育供給側結構性改革，推進高等職業教育與區域經濟適應性戰略調整，強化西部地區高等職業教育集群化發展來促進兩者協同發展。

關鍵詞 高等職業教育規模;區域經濟;耦合協調度;灰色預測;西部12省（市、自治區）

中圖分類號 G718.5 文獻標識碼 A 文章編號 1008-3219（2020）21-0051-06

自1999年高校擴招以來，我國高等教育毛入學率從1999年的10.5%躍至2018年的48.1%，高等教育從精英化邁入普及化軌道。在此背景下，高等職業教育也得到快速發展。2018年高職（專科）院校招生368.8萬人，占普通本專科招生總人數的46.6%，約占高等教育的半壁江山。當前，我國經濟已步入新常態，區域經濟發展方式的轉變、產業結構的優化升級、行業技術的創新以及科技成果的轉化等，不僅需要一大批有較高理論水平的科研人才，更需要一支有知識、會技能、懂技術、能創新的高技能型人才隊伍，將科學技術轉化為現實生產力，而高等職業教育以培養高素質技術技能人才為目標，與區域經濟發展需求具有較高契合度，是與區域經濟發展關系最為密切的高等教育類型，勢必成為推動區域經濟發展、產業結構轉型升級的重要力量。因此，加快發展現代高等職業教育，優化人才結構，擴大有效供給，培養一大批勇于創新、善于創新的高素質技術技能型人才，服務區域經濟的高質量發展，是擺在我們面前的一項緊迫任務。

西部地區包括內蒙古、新疆、寧夏、青海、甘肅、陜西、四川、重慶、云南、貴州、廣西、西藏12個省（市、自治區），約占全國國土面積的3/4。2018年西部地區GDP總量占全國的20.5%，高校數量占全國的26.1%，普通高校在校生占全國的25.9%。總體來看，西部地區的經濟、高等教育都保持著良好的發展勢頭。邁向新時代，西部地區更要主動融入“一帶一路”建設，以西部地區全方位開放為著力點，依托自身區位優勢，拓展區域經濟、高等教育發展新空間，強化基礎設施互聯互通，增強沿線經濟帶和城市群的連接性，推動西部發展動力轉換、結構的轉型升級和共享發展，最終把西部建設成為我國向西、向北、向南開放的橋頭堡。因此，探究西部12省（市、自治區）高等教育與經濟發展間的關聯性，對我國區域經濟社會的協調發展、跨越發展具有重要的現實意義。本研究以西部12省（市、自治區）為研究對象，通過構建高等職業教育規模與區域經濟發展水平指標體系，分析兩者的耦合協調發展狀況，并在此基礎上提出相應的對策建議，以期為新時代我國高等職業教育規模擴張與均衡發展提供參考借鑒。

一、數據來源、指標體系與研究方法

（一）數據來源

本研究選取西部12省（市、自治區）2008-2017年的面板數據，且每一項指標數據始終來自一種年鑒。其中，高等職業教育的院校數、招生數、在校生數和畢業生數來源于《中國教育統計年鑒》（2008-2017年），地區生產總值、人均地區生產總值、年末人口數、第二產業占GDP比重、第三產業占GDP的比重、城鎮居民人均可支配收入、農村居民人均可支配收入、地方財政收入均來自于《中國統計年鑒》（2008-2017年）。為了消除通貨膨脹對經濟規模增長的影響，以2008年為基期計算獲得2008-2017年西部12省（市、自治區）GDP和人均GDP的面板數據。研究的數據來源可靠，具有較高的信效度。

（二）指標體系

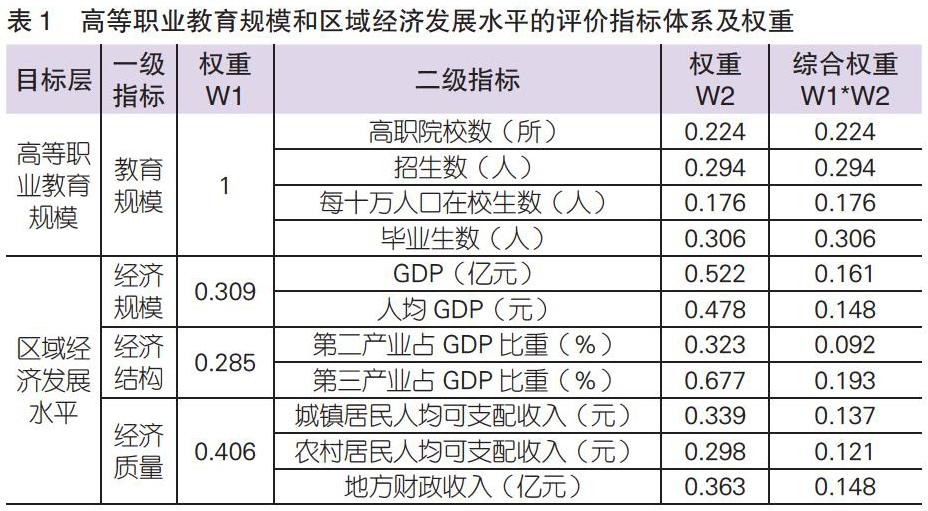
本研究以高等職業教育規模和區域經濟發展水平為目標層，設計了測度兩者關系的指標體系。其中，高等職業教育規模由1個一級指標、4個二級指標構成，區域經濟發展水平由3個一級指標、7個二級指標構成。同時，采用客觀賦值法——熵值法[1]確定各級指標的權重。具體結果見表1。

（三）研究方法

1.綜合評價模型

對西部高等職業教育規模和區域經濟發展水平的協調性進行綜合評價，設a1，a2，…，am為描述西部高等職業教育規模的m個指標，設b1，b2，…，bn為區域經濟發展水平的n個指標，則其綜合評價模型[2]分別為：

其中，f（x）為高等職業教育規模的綜合評價指數;g（y）為區域經濟發展的綜合評價指數。

2.耦合協調度模型

耦合度主要是描述兩個或以上系統（要素）之間的關聯程度，而協調度則是測量系統或要素間耦合協調狀況好壞程度的指標模型[3]。本研究采用離差系數最小化耦合度模型，對西部高等職業教育規模與區域經濟發展水平的相互作用機理進行探究。兩者的耦合度越接近1，表明高等職業教育規模與區域經濟發展水平間的關聯度越強;反之則表明系統間的關聯度差。其耦合度公式[4]為：

其中，C為耦合度，取值范圍為0≤C≤1。若0

耦合度C只能反映高等職業教育規模與區域經濟發展水平兩個系統間交互影響的強弱，但難以測算其整體的“功效”和“協同”。為了更加準確地度量出高等職業教育規模與區域經濟發展水平的協同度，本研究在耦合度基礎上引入耦合協調度模型[5]，其公式為：

其中，CD為耦合協調度;T為耦合協調發展水平的綜合評價指數;α、β均取0.5（高等職業教育規模與區域經濟發展水平同等重要）。若耦合協調度越大，說明高等職業教育規模與區域經濟發展水平之間達到良性的共生耦合，其發展越協調越好;反之亦然。根據現有研究將耦合協調度進行等級劃分，具體見表2。

3.修正GM（1，1）預測模型

灰色預測模型是基于灰色系統理論而建立的，它適用于對小樣本、貧信息、不確定性的系統進行時間序列的預測。本研究通過構建等維遞補數列對傳統的GM（1，1）模型[6]進行修正，即用已知數列建立GM（1，1）模型獲得一個預測值，然后將這個新的預測值補充到已有數列中，同時去掉最老的那個數據，并使序列等維，進而再建立GM（1，1）模型，這樣依次遞補，逐個滾動預測，直至完成預測目標。具體步驟如下：

首先，設原始時間序列為X0=﹛X0（1），X0（2），…，X0（n）﹜，通過對原始序列X0進行累加生成序列X1=﹛X1（1），X1（2），…，X1（N）﹜，構造矩陣B、Yn，則其相應的微分方程為：

式中，a為發展灰度，?為內生控制灰數。

其次，設待估參數向量為β︿=a/?，利用最小二乘法解β︿=（BTB-1）BTYn，求解微分方程，可得預測模型為：

最后，對預測模型進行精度檢驗，若檢驗結果同時滿足P>0.7且C﹤0.65，則可計算該項指標的預測值，否則要通過殘差模型修正。

二、研究過程與結果分析

（一）高等職業教育規模系統與區域經濟系統綜合發展水平分析

基于綜合評價模型，測算出西部12省（市、自治區）高等職業教育規模系統和區域經濟系統的綜合評價指數，見圖1、圖2。從中可以發現，西部高等職業教育規模和區域經濟兩大系統具有較強相似性。西部地區高等職業教育規模和區域經濟兩大系統均呈上升態勢，但發展水平不高，發展緩慢，且發展過程中存在明顯波動，2012-2013年為兩大系統發展的低谷期。兩大系統發展均呈明顯的分層現象，大致可以分為三大梯隊，基本上四川、陜西、重慶位居第一梯隊，內蒙古、廣西、貴州、云南、甘肅、新疆位居第二梯隊，寧夏、青海、西藏為第三梯隊。一方面說明高等職業教育規模與區域經濟具有較高的關聯度，另一方面表明西部地區兩大系統存在較大省際差異。

除此以外，兩大系統的發展存在一定的差異性。從兩者的動態變化曲線看，區域經濟的變化較為緩和，省際間經濟發展水平格局與變化幅度較為穩定，而高等職業教育規模變化的波動較大，表明西部12省（市、自治區）間高等職業教育規模發展水平差異將長期存在，且在短期內難以有效轉變。西部地區高等職業教育規模發展水平一直高于區域經濟發展水平，整個區域屬于經濟發展滯后型，即高等職業教育規模的快速發展對區域經濟發展具有較大的促進作用，而區域經濟對高等職業教育規模擴大的驅動作用較為薄弱。西部12省（市、自治區）高等職業教育規模與區域經濟系統綜合評價水平可以分為三個類別：一是高等職業教育規模超前型，即高等職業教育規模驅動區域經濟發展，主要有四川、貴州、陜西、甘肅、廣西5省（自治區）;二是高等職業教育規模滯后型，即高等職業教育規模驅動作用尚不明顯，主要有西藏、青海、寧夏、內蒙古4省（自治區）;三是高等職業教育規模趕超型，即高等職業教育規模逐漸超過區域經濟發展水平，主要有重慶、云南、新疆3省（市、自治區）。

（二）高等職業教育規模與區域經濟發展系統耦合度的時序變動分析

根據耦合度公式，計算出西部12省（市、自治區）2008-2017年的高等職業教育規模與區域經濟發展水平的耦合度，具體結果見表3。

整體而言，西部地區高等職業教育規模與區域經濟發展水平系統之間具有較好的同步性，存在耦合互動發展關系。2008-2017年間西部地區的耦合度呈波動下降趨勢，年均下降0.085%，降幅不大，總體上其耦合度較高，均在0.9以上，處于高水平耦合階段。從各省份來看，僅有西藏的耦合度較低，處于拮抗階段，說明該省的高等職業教育規模與區域經濟發展水平之間還沒有形成合力，系統間仍處于相互制約的狀態;其余11省（市、自治區）的耦合度均在0.8以上，處于高水平耦合階段，說明其高等職業教育規模與區域經濟發展水平兩個系統之間已經達到相互促進、共同發展的良性共振耦合階段，區域經濟發展對高等職業教育規模擴大起到極大推動作用，同時高等職業教育的發展對區域經濟的促進和支撐作用也越來越明顯。從縱向來看，貴州、云南、寧夏、廣西、內蒙古5省（自治區）高等職業教育規模與區域經濟發展水平兩個子系統之間的交互協調程度呈下降趨勢，年均降幅最大的為貴州，下降了1.176%，總體來說，這些省份的降幅均不明顯;區域間的耦合度差距不斷縮小，2008年區域間耦合度最高值與最低值的差距為0.67，2017年區域耦合度最大的新疆與耦合度最小的西藏相差0.66。

（三）高等職業教育規模與區域經濟發展系統耦合協調度的時序變動分析

根據耦合協調度公式，測算出西部12省（市、自治區）高等職業教育規模與區域經濟發展水平的耦合協調度，具體結果見表4。

10年間，西部地區高等職業教育規模與經濟發展的耦合協調度呈小幅上升的良好態勢，從0.597上升至0.616，漲幅3.18%，協調等級由勉強耦合協調水平上升至初級耦合協調水平，類型為過渡調和類。由此表明，西部地區經濟增長方式的轉變，產業結構的優化調整，逐漸增強了高等職業教育規模與經濟發展的耦合互動效應，耦合協調度不斷優化，兩個系統的耦合協調關系正向著良性方向發展。

從區域分布來看，存在明顯的省際差異。其中，僅有重慶、四川、陜西、廣西、內蒙古、云南6省（市、自治區）高于西部均值，其余6省的耦合協調度均低于西部平均值。2008-2017年間，四川的耦合協調度始終是最高的，在2008年已經達到良好耦合協調水平，而西藏的耦合協調度一直處于最低水平，始終位于中度失調衰退區間，且兩者的耦合協調度差距在擴大。貴州、重慶的耦合協調度上升幅度最大，漲幅18.54%、12.22%;廣西、寧夏的下降幅度最大，減幅7.79%、6.48%;陜西、內蒙古小幅下降，降幅分別為2.89%、2.32%;青海、新疆、甘肅、云南、四川、西藏均有上升，漲幅分別為7.85%、7.62%、7.2%、5.77%、3.75%、0.43%。與2008年相比，2017年四川、重慶、內蒙古、陜西、云南、甘肅、寧夏、西藏的協調等級不變，四川位于良好耦合協調區間，重慶、內蒙古、陜西位于中級耦合協調區間，云南位于初級耦合協調區間，甘肅位于勉強耦合協調區間，寧夏位于瀕臨失調衰退區間，西藏位于中度失調衰退區間;廣西下降1個協調等級，位于初級耦合協調區間;貴州、新疆、青海上升1個協調等級，貴州、新疆均位于初級耦合協調區間，青海位于瀕臨失調衰退區間。綜合來說，西部地區的耦合協調水平仍然很低，但大多數省的耦合協調度呈上升趨勢，省域差距逐漸拉大;初級耦合協調、瀕臨失調衰退省份所占的比重有所增加，勉強耦合協調和中級耦合協調的省份在逐年減少，良好耦合協調省份經歷了少—多—少的變化;制約各省耦合協調發展的因素有高等職業教育規模滯后性和經濟發展水平滯后性。由此可見，西部地區各省（市、自治區）的耦合協調水平雖然起點不同、差距明顯，但經過10年的發展，大部分省（市、自治區）的耦合協調度均有所提升，其協調發展水平具有較大的提升空間。

（四）西部地區耦合協調度發展預測

根據GM（1，1）預測模型，可以計算出西部12省（市、自治區）2018-2022年兩大系統的耦合協調度預測值，具體結果見表5。

未來五年，西部地區高等職業教育規模與區域經濟發展的耦合協調度呈上升趨勢，但仍處于初級耦合協調水平。各省的耦合協調度發展將大致延續2008-2017年變化特征，四川、重慶依然是耦合協調水平最高的區域，四川將率先突破良好耦合協調等級，預計2021年達到優質耦合協調，重慶將由中級耦合協調到2018年上升到良好耦合協調，這兩個省（市）對高等職業教育和科技創新的資源投入相對較多，入選“雙高計劃”的高職院校數量也相對較多，優質高職院校集聚效應顯著，增強了城市的創新創業活力，拉動了經濟的進一步發展，為兩省（市）持續強化的良性發展提供了較大機會，更起到了引領效應;貴州、新疆、甘肅、青海4省的耦合協調度均有小幅上升，雖未能實現向更高等級演進，但這些省的協調互動效應進一步增強;內蒙古、陜西、廣西、云南、寧夏5省（自治區）的耦合協調度有所下降，但其耦合協調等級均保持不變，這些省份更應主動抓住“一帶一路”建設的發展機遇，推動高等職業教育與區域經濟的相互對接、優勢互補和共同發展。預測結果顯示，西部地區高等職業教育規模與區域經濟發展未來五年的耦合協調水平與演進速度較慢，大部分省份仍處于勉強耦合協調—中級耦合協調水平之間，且省域間耦合協調度差異將進一步擴大。

三、研究結論與對策建議

（一）研究結論

研究基于2008-2017年的統計數據，構建評價指標體系，并運用熵值法、耦合協調度模型及修正GM（1，1）模型對西部12省（市、自治區）高等職業教育規模與區域經濟發展水平系統的耦合協調發展及預測進行了實證分析，得出以下三個結論：一是西部地區高等職業教育規模系統與區域經濟系統的發展水平均呈波動上升態勢，高等職業教育規模系統的綜合評價指數明顯高于區域經濟發展系統，且高等職業教育規模系統發展水平更具波動性。西部地區高等職業教育規模對區域經濟發展的促進作用較為突出，而區域經濟發展對高等職業教育規模的驅動作用還比較微弱。二是西部地區高等職業教育規模與區域經濟發展兩個系統存在明顯的耦合互動發展特征，其中，耦合度有所下降，但始終處于高水平耦合階段。耦合協調度呈小幅上升良好態勢，由勉強耦合協調水平上升至初級耦合協調水平。省際間跨越等級不同，均未達到優質協調等級，造成該區域兩大系統耦合協調度省際差異的重要原因是高等職業教育規模系統與區域經濟發展系統的綜合評價值在空間上均存在較大差異。三是通過預測，未來五年西部地區高等職業教育規模與區域經濟發展的耦合協調度將穩步提升，但仍處于初級耦合協調水平。省際間協調發展演進速度差異將更加明顯，其中，僅有四川將率先突破良好耦合協調進入優質耦合協調等級，重慶由中級耦合協調到2018年上升至良好耦合協調，其余10省份的耦合協調等級保持不變。

（二）對策建議

西部地區具有得天獨厚的資源條件和巨大發展潛力，在我國區域發展總體格局中具有重要戰略地位。為推動新常態背景下西部12省（市、自治區）高等職業教育規模與區域經濟發展的協調發展，本研究從宏觀角度提出以下政策性建議：

第一，深化高等職業教育供給側結構性改革。在擴大規模的同時更加注重質量提高，以尋求高等職業教育與區域經濟之間的平衡點。高等職業教育規模與區域經濟發展的耦合協調度問題，其實質就是整個高等職業教育供給側結構性問題，更體現高等職業教育的規模與質量問題，高等職業教育并不應是追隨經濟發展，而應是引領經濟發展，從而推動經濟發展的質量變革、效率變革和動力變革。在經濟發展速度放緩、產業結構調整優化的新常態下，西部各省（市、自治區）的高職院校要主動融入“一帶一路”、西部大開發和長江經濟帶建設，及時把握產業結構動向和發展趨勢，適時優化學科專業布局結構，使人才培養鏈與產業鏈有效對接，提高人才供給和輸出質量，整體上達到高等職業教育規模與區域經濟發展的耦合協調。

第二，推進高等職業教育與區域經濟適應性戰略調整。要合理利用西部各省（市、自治區）的本土資源和優勢，制定適宜的發展戰略。四川、陜西、甘肅、貴州、廣西等高等職業教育規模超前型省份，應發揮區域內的帶頭作用，把高等職業教育規模優勢作為區域經濟發展的“驅動性資源”，通過制定產業發展政策，推進工業轉型升級，優化產業布局，提升高等職業教育規模系統與區域經濟發展系統的協調發展水準。西藏、青海、寧夏、內蒙古等高等職業教育規模滯后型省份，應加大對該地區教育資源的扶持，加大高等職業教育財政投入力度，制定相應的人才引進政策，完善地區基礎設施建設，吸引外來人才、留住本地人才，為高等職業教育規模的擴大提供更好的環境，提升高等職業教育質量，以達到與區域經濟發展匹配狀態。重慶、云南、新疆等高等職業教育規模趕超型省（市、自治區），其高等職業教育與區域經濟發展的水平都不高，因此，應將發展高等職業教育作為區域經濟跨越式發展的突破口，通過優先發展高等職業教育，加強高水平高職學校和高水平專業群建設，提高技術技能型人才培養的數量和質量，以人才智力資源助推區域經濟發展。

第三，強化西部區域高等職業教育集群化發展。高等職業教育集群是高等教育結構布局在地域空間上的特殊表現狀態，眾多高職院校基于資源共享、成本分擔、績效提升集聚在一起形成區域性大學群落，其具有相對完整的地域性特征，教育圈、經濟帶、城市群、產業鏈高度耦合，多產業相融、多機構相聯、多條約相依，經濟、社會、政治、文化和生態融為相互依存的共生體，能夠集聚高等職業教育資源，增強高職院校規模效應，提升服務區域經濟發展的能力。從省際層面來看，西部12省（市、自治區）的高等職業教育資源是有限的，因此，想要實現高等職業教育規模與區域經濟的協調發展，就必須推動西部各省（市、自治區）高等職業教育聯動改革，打破區域行政壁壘，通過強化重慶、成都、西安等國家中心城市建設，增強成渝城市群、北部灣城市群、關中平原城市群、呼包鄂榆城市群與蘭西城市群合作，形成高等職業教育區塊鏈，推動高等職業教育集群的互動融合，促進高、低耦合協調區資源、要素合理流動，最終實現高等職業教育規模與區域經濟資源的優化組合。

參 考 文 獻

[1]朱喜安，魏國棟.熵值法中無量綱化方法優良標準的探討[J].統計與決策，2015（2）：12-15.

[2]姜璐，李玉清，董維春.我國高等教育結構與產業結構的互動與共變研究——基于系統耦合關系的視角[J].教育科學，2018（3）：59-66.

[3]劉雷，張華.山東省城市化效率與經濟發展水平的時空耦合關系[J].經濟地理，2015（8）：75-82.

[4]彭新一，王春梅.區域高校科技創新能力與經濟發展水平耦合協調研究[J].科技管理研究，2018（3）：148-155.

[5]宋美喆，李孟蘇.高等教育、科技創新和經濟發展的耦合協調關系測度及其影響因素分析[J].現代教育管理，2019（3）：19-25.

[6]王璐，沙秀艷，薛穎.改進的GM（1，1）灰色預測模型及其應用[J].統計與決策，2016（10）：74-77.