基于歐式距離角點提取的工業機器人視覺算法

趙瀟安

（桂林電子科技大學 電子工程與自動化學院，桂林541004）

工業機器人在物體抓取、自動裝配、噴涂、搬運碼垛、焊接等場合的應用越來越廣泛[1]。 與使用傳統的示教方法搭建機器人抓取系統相比較，基于視覺的工業機器人抓取系統， 提升了其靈活性和穩定性，極大地拓寬了工業機器人的應用空間。

在2D 相機的工業機器人視覺研究中， 文獻[2]使用發那科FANUC 機器人通信模塊與標定算法，通過圖像處理提取輪廓中心為特征點；文獻[3]提出基于圖像梯度優化與評分的方法，以解決目標物體的識別與定位問題；文獻[4]采用最小二乘算法擬合直線， 然后根據直線計算目標物體的傾斜角度；文獻[5]提出基于直線特征的位姿測量方法SoftNewton，構建了直線的匹配評價函數， 再采用高斯牛頓迭代算法解算目標位姿；文獻[6]采集2 幅圖像通過雙視圖幾何的等效約束來解算目標物體的旋轉姿態角度。

為了有效地提取目標物體的姿態角度信息，在此提出根據聚類中心之間中點與角點之間的歐式距離提取角點的方法，然后以角點作為特征點提取虛擬向量，采用相互匹配的向量計算出目標物體的姿態角度。

1 工業機器人圖像數據采集平臺搭建與圖像預處理

1.1 工業機器人圖像數據采集平臺

為了通過圖像獲取工業機器人的末端姿態數據，搭建工業機器人圖像數據測量平臺。 平臺硬件由垂直多關節六自由度重復定位精度為0.03 mm 的機器人，圖像分辨率為2048×1536 和水平/垂直像素為3.45 μm×3.45 μm 的攝像機， 以及工業計算機等組成。

在工業機器人視覺系統中，上位機通過以太網總線的通信方式與工業機器人控制系統通信。圖像處理軟件采用德國MVtec 公司研發的HALCON機器視覺軟件， 利用導出的C# 文件開發工業機器人通信模塊。 工業機器人圖像數據測量平臺如圖1所示。

1.2 工業機器人視覺系統標定與攝像機圖像畸變矯正

圖像數據測量平臺攝像機安裝方式采用eyeto-hand 結構，將工業攝像機固定在支架末端。 通過手眼標定計算得到工業攝像機坐標系在工業機器人基坐標系中的位置。 使用文獻[7]的標定算法得到攝像機內外參數，通過計算獲得圖像的內部參數與標定板所處平面坐標系相對于相機坐標系的轉換關系。

畸變圖像以及通過圖像畸變矯正后得到圖像的復原圖，如圖2 所示。

2 目標物體幾何元素計算

目前， 基于2D 視覺的工業機器人抓取系統多采用SIFT，SURF[8-9]等特征檢測算法。 然而，這些算法的特征點檢測依賴于尺度空間的選擇，在實際使用過程中不可避免地存在特征點的漏檢。

2.1 粗角點計算

在圖像的微觀結構中，圖像的邊緣輪廓由微小的像素構成。 以三角柱和立方體的平面拍攝圖為例，目標物體的角點作為特征點。在此通過模板a 與模板b 遍歷圖像中所有的邊緣像素點，若該像素點擁有2 個灰度變換方向，則保留該點為粗角點。

2.2 基于兩個聚類中心之間的中心點角點估計

在幾何目標物體的平面圖中，輪廓可以被描述為由多個三角形組成。 在如圖3 所示立方體的輪廓內可以提取出三角形r1，r2；在如圖4 所示六棱柱的平面圖中可以提取出三角形R1，R2，R3。 由此分析可知，角點的分析涉及構成幾何的基本單元——三角形。 故在此對典型的基本單元三角形進行角點提取的研究。

圖3 立方體平面圖輪廓三角形劃分Fig.3 Cube plan view outline triangle division

圖4 六棱柱平面圖輪廓三角形劃分Fig.4 Hexagonal prism plan view outline triangle division

邊緣鋸齒以及角點、偽角點與輪廓內一點之間的歐氏距離如圖5 所示。 圖中，圖像中存在邊緣鋸齒等干擾因素，造成在角點檢測中存在大量的偽角點。 在閉合輪廓中，真角點與輪廓內其它點的歐式距離存在唯一性，并且存在歐式距離最大值。

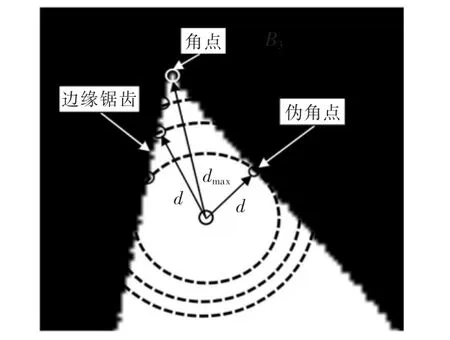
圖5 邊緣鋸齒以及角點、偽角點與輪廓內一點之間的歐氏距離Fig.5 Edge jagged and Euclidean distance between corner，false corners and a point in the contour

由圖可見，輪廓內的點與角點之間的歐式距離為dmax，與偽角點之間的歐式距離為d，dmax＞d。 故在此提出計算歐式距離最大值的方法，通過歐式距離剔除由于偽角點引入的不穩定因素。

2.3 角點提取

為了得到更加準確的角點，在圖像處理過程中引入k-means++修正算法[10]。通過上述方法計算出粗角點之后，選擇合適的聚類中心數，計算獲得所需的聚類中心。

2.3.1 基于兩個聚類中心之間的中心點角點提取

計算出聚類樣本與聚類中心之后，可計算出其中2 個聚類中心之間的中心點坐標。 如圖6 中聚類中心點ci與中心點cˉ所示，有

如圖6 所示，計算中心點分別與其它聚類樣本內的粗角點（真角點與偽角點）之間的歐式距離d 為

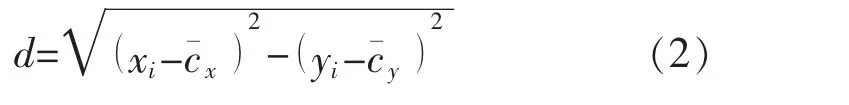
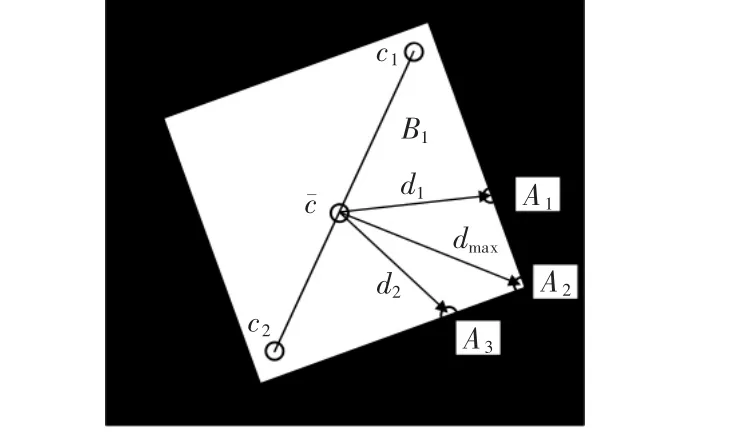
圖6 聚類中心的中心點與粗角點之間的歐式距離Fig.6 Euclidean distance between the central point of the cluster center and the rough corners

在其它聚類樣本內，分別保留擁有最大值d 的對應粗角點為真實角點。在圖6 所示B1區域內，dmax＞d1，dmax＞d2，保留擁有最大值dmax的粗角點即A2為真角點。 使用其它的聚類中心組合與聚類樣本可重復以上計算過程，計算出各個角對應的角點。

2.3.2 驗證

為提高角點識別的正確率，對所提取的角點進行驗證。

步驟1在提取出的真實角點之間計算中心點，類似于式（1），重新計算中心點。

步驟2在各個聚類樣本中， 重新計算新得到的中心點與粗角點（真角點與偽角點）之間的歐式距離，保留歐式距離最大的對應角點為真實的角點。

步驟3在每一個聚類樣本中， 選取與驗證前不同的中心點， 估計同一角點。 分2 種情況進行討論：

情況1計算出2 個角點。 若驗證前與驗證后得到的角點相同，則該點為最終計算真角點；

情況2若驗證前與驗證后得到的角點不相同，則重新計算2 個角點與對應的聚類中心之間的距離，距離最小者為最終計算的真角點。重復步驟1至步驟3，直至所有的角點驗證完畢，得到目標物體的所有的真角點。

3 虛擬向量提取與姿態旋轉角度計算

3.1 虛擬向量提取

在立方體平面圖中，采用與對角線平行的虛擬向量L1與L2為特征向量。 三角柱平面圖中采用與三角柱的邊平行的L1′和L2′為虛擬向量， 并以此作為特征向量。 三角柱平面圖與立方體平面圖的虛擬向量如圖7 所示。

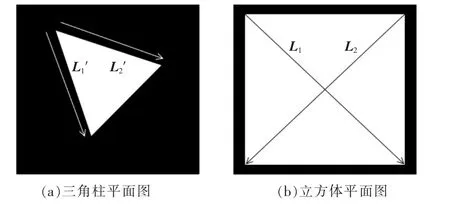
圖7 平面圖的虛擬向量Fig.7 Virtual vectors of floor plan

3.2 根據虛擬向量計算姿態旋轉角度

目前，目標物體的姿態旋轉角度計算方法主要采用SIFT 算法和SURF 算法等提取圖像中的特征點，通過估算仿射參數計算姿態旋轉角度。 文獻[11]提出采用BRIEF 描述子對SURF 算法提取的特征點進行描述，結合最近漢明距離融合PROSAC 算法提高特征點的匹配精度。

文獻[12]將軟決策技術和POSIT 算法[13]結合，形成SoftPOSIT 算法。 文獻[14]采用尺度不變特征變換SIFT 算法計算特征點，采用特征點主方向匹配特征點并且計算姿態旋轉角度，算法計算誤差約為3°。

本文算法也采用假設與檢驗的方法，通過相互匹配的特征向量之間的夾角計算姿態旋轉角度。 立方體起始姿態如圖8 所示，先使用相機拍照一個固定放置目標物體的圖像，將其作為模板圖像，且目標物體的起始姿態為0°。 姿態的計算目的，就是獲得從模板圖像到實際目標的變化包括姿態旋轉角度，從而為工業機器人末端抓取提供移動信息。

圖8 立方體起始姿態Fig.8 Origin posture of the cube

在圖像坐標系中， 立方體姿態旋轉角度θ 為30°，如圖9 所示。 立方體相對于模板圖像的起始位置出現了姿態旋轉角度θ，即目標圖像。 由于姿態旋轉角度的唯一性，通過目標圖像與模板圖像中目標物體之間的比較，獲得工業機器人末端抓取的姿態旋轉角度。

圖9 立方體姿態旋轉角度30°Fig.9 Cube posture rotation angle of 30 degrees

通過本文算法計算出目標物體的姿態旋轉角度。 針對立方體平面圖的4 個角點與三角柱平面圖的3 個角點，以2.3 節獲得的角點為基礎，目標圖像的虛擬向量、模板圖像的虛擬向量為

式中：（xi，j，yi，j）為模板圖像的角點坐標，i=1，2，且j=1，2；（Xi，j，Yi，j） 為目標圖像的角點坐標；i 為對應虛擬向量標號；j 為虛擬向量對應的角點坐標序號。

計算出目標物體的特征向量之后。 首先假設目標圖像與模板圖像之間的其中一對特征向量相互匹配。 特征向量之間的夾角為

式中：假設L1與l1為互相匹配的特征向量；θ 為計算的旋轉輸出角度。 根據輸出角度，計算仿射參數矩陣，并投影余下的特征向量。 即

通過檢驗另外一條特征向量是否重合確定姿態，增加算法的穩定性。 若另外一條特征向量沒有重合則重新匹配，計算出正確的姿態角度。

4 對角點識別和姿態角度估計算法驗證

4.1 角點識別精確度分析

目標物體的邊緣輪廓存在角點，如圖10 所示。為了提取更加精確的角點，在此進行了方法的對比。 采用文獻[15]所述方法根據角度閾值提取角點，試驗中以粗角點兩邊夾角＞8°為閾值。基于歐氏距離的角點識別方法，提取出聚類中心之中心點與其它樣本內歐式距離最大的粗角點為真角點。

圖10 立方體邊緣輪廓角點Fig.10 Corners of cube edge contour

角點的識別精度見表1。由表可知，基于歐氏距離的角點識別方法識別精確度高，對所提方法的實現具有更好的使用效果。

表1 角點識別精度Tab.1 Corner recognition accuracy

4.2 目標物體姿態角度估計誤差結果

通過試驗驗證本文算法，選取立方體與三角柱為試驗圖像。 目標物體的姿態旋轉角度，如圖11 所示。

在圖像坐標系中，三角柱圍繞旋轉中心點從5°旋轉至60°， 立方體圍繞旋轉中心點從5°旋轉至85°。 在圖像處理過程中，圖像沒有噪聲等干擾的情況下，目標物體沒有發生平移變換。

采用所提出的目標物體姿態角度估計算法，評估姿態角度的誤差。 三角柱和立方體的姿態角度計算誤差如圖12 所示。

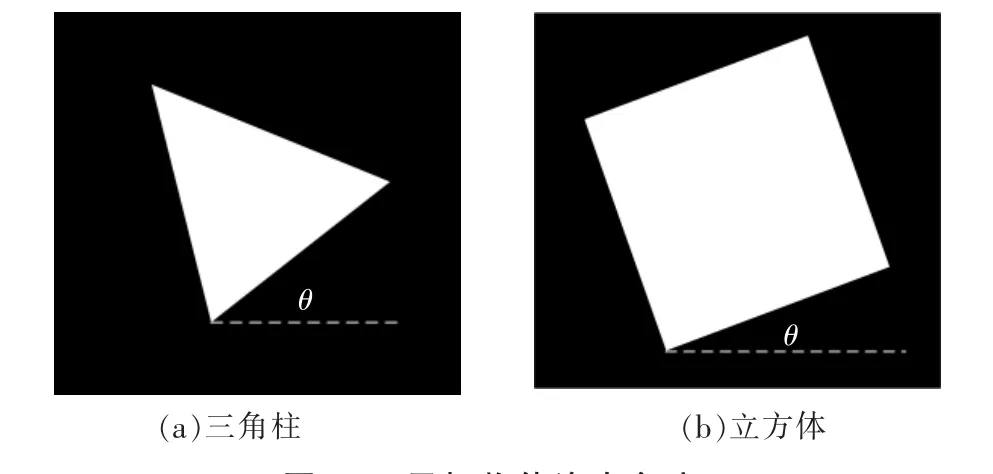
圖11 目標物體姿態角度Fig.11 Posture angle of target object

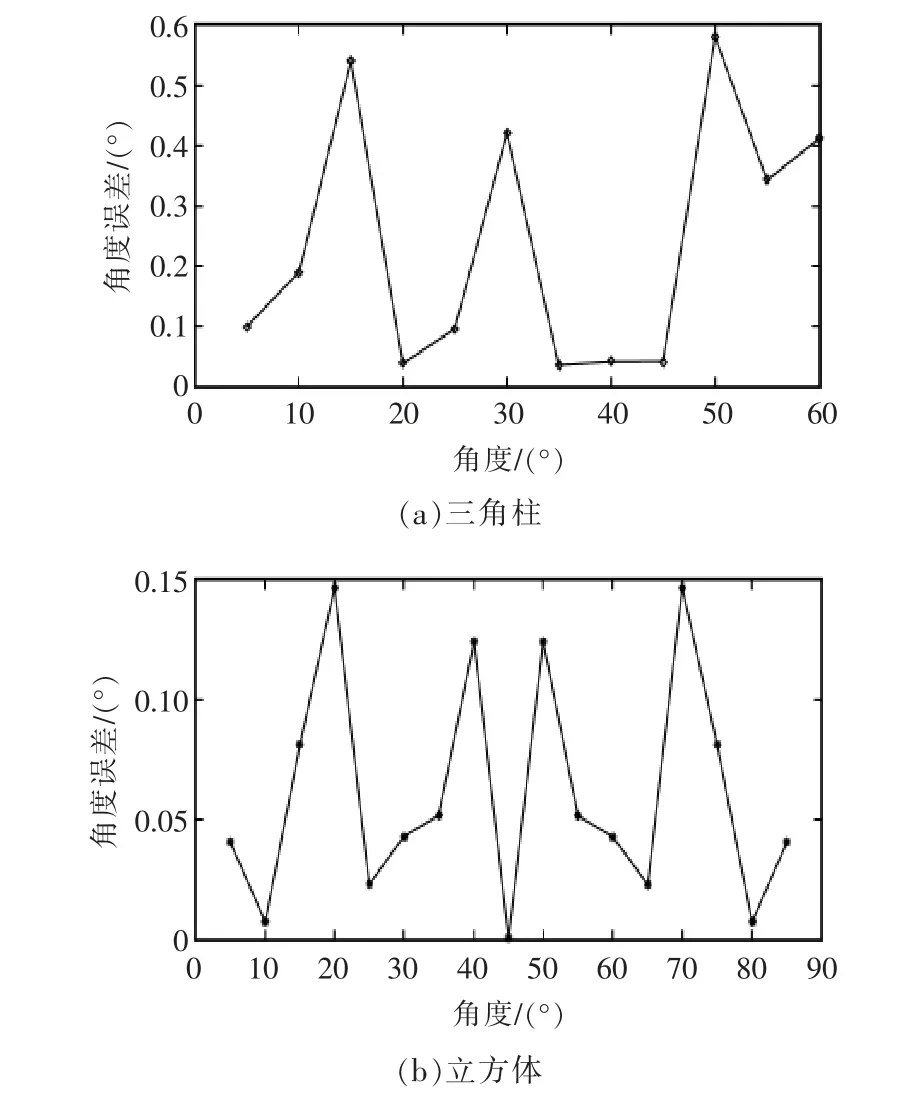
圖12 目標物體姿態角度的計算誤差Fig.12 Calculation error of posture angle of target object

由圖可見，立方體的姿態從0°旋轉至85°，最大誤差達到0.1474°，平均誤差為0.0610°；三角體的姿態從0°旋轉至60°，最大誤差達到0.5828°，平均誤差為0.2367°。 SIFT 算法對于分辨率為640×480 的圖像提取特征點需要1.75 s， 分辨率為320×240 的圖像提取特征點所需時間為0.63 s； 本文算法運行時間小于0.2 s，縮短了圖像中目標物體姿態旋轉角度的測量時間。

4.3 姿態旋轉角度估計算法試驗對比分析

試驗中，利用圖11 所示立方體的平面圖與三角柱的平面圖為試驗對象。 采用尺度不變特征變換SIFT 算法提取圖像特征點，計算出模板圖像與目標圖像中對應匹配的3 個特征點后，采用三點法計算出仿射參數與姿態旋轉角度。

三角體的姿態旋轉角度分別為5°，10°，15°，20°，25°，30°，35°； 立方體的姿態旋轉角度分別為5°，10°，15°，30°，35°，40°，45°，50°，55°，60°，75°，80°，85°。 本文算法與SIFT 算法的估計誤差對比結果如圖13 所示。

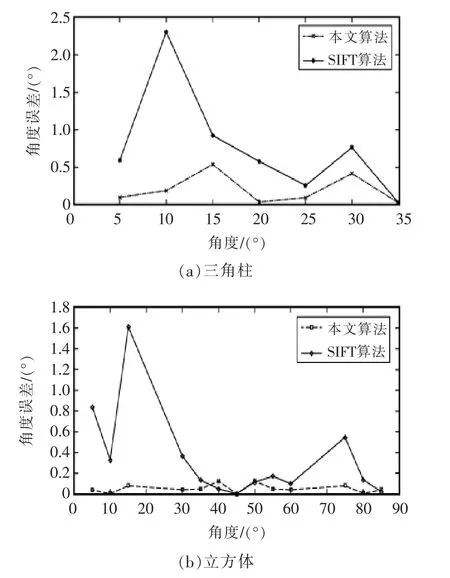
圖13 目標物體姿態角度估計誤差的對比Fig.13 Comparison of posture angle estimation errors of target objects

估計誤差的試驗對比結果見表2。 通過試驗對比，本文提出的算法在物體旋轉姿態角度估計上準確度優于SIFT 算法。

表2 姿態角度估計誤差的對比結果Tab.2 Comparison results of posture angle estimation error

5 結語

在工業機器人末端目標物體的姿態獲取中，角點的準確提取為一個關鍵技術。 所研究的圖像可以抽取為多個三角形組成的獨立單元。 在各個獨立的三角形中，根據2 個聚類中心之間中點與角點之間的歐式距離為依據，提取擁有最大值的粗角點為真角點。 以角點構成圖像的特征向量，采用假設與檢驗的方法將模板圖像與目標圖像中的特征向量相匹配，以相匹配的特征向量之間的夾角作為目標物體的姿態旋轉輸出角度，所獲得工業機器人的末端姿態，為視覺抓取提供必要的參考數據。 基于試驗采集圖像數據進行了處理與分析，與尺度不變特征變換SIFT 算法作比較。 試驗結果表明，所提出的方法用于目標物體的旋轉角度估計具有較高的準確度，在實時性方面也表現出一定的優勢。