地磁模型構建仿真及匹配特征量的選擇

彭 飛，熊 凌，陳 洋

（1.武漢科技大學 機器人與智能系統研究院，武漢430081；2.武漢科技大學 信息科學與工程學院，武漢430081）

地磁場是由地球內部液態鐵的流動，以及地球內部和外部的電流體系，所產生的各種磁場組合疊加而產生的[1-2]。 近些年，隨著地磁場模型、地磁測量設備、地磁信息處理技術等研究的不斷發展，使得地磁匹配導航技術逐漸成為導航技術研究領域熱點之一。 目前，地磁匹配導航技術的研究主要集中在匹配算法上，對于匹配導航基準圖的研究則較少，但一些具有代表性的地磁匹配算法，如TERCOM 算法[3-4]、ICCP 算法[5-6]為基礎的地磁導航算法等都是基于地磁圖的匹配定位方法。 因此，在地磁匹配導航技術的研究中，地磁基準圖的構建具有重大意義。

地磁基準圖的構建主要有模型法和實測法2種。 前者主要用于地磁場性質的研究，而高精度地磁圖的構建主要依賴后者[7-8]。 國際地磁參考場（IGRF）是用來描述地球的主磁場及其變化的地磁模型。 該模型自1900 年開始，每5 年進行一次更新換代，迄今為止已更新到第13 代，IGRF13 的相關系數也于2019 年12 月發布。 在此，主要利用IGRF13 的相關系數來構建地磁基準圖，并對地磁分量進行分析，選擇適用于地磁導航的地磁信息。

1 地磁場模型構建及分析

1.1 地磁場模型構建

地磁場是一個矢量場，是一個空間與時間相關的函數[9-10]。可以采用圖1 所示的空間坐標系來表示地磁場各要素之間的相互關系及其空間分布特點。

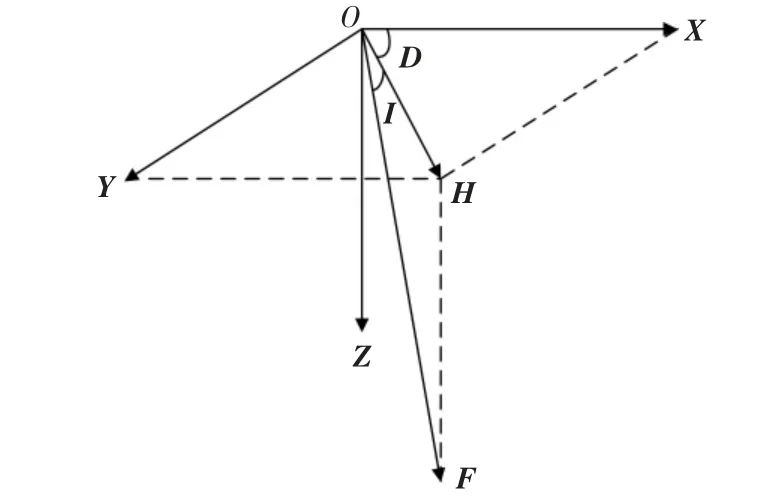
圖1 地磁場元素結構Fig.1 Structure of geomagnetic elements

在該坐標系中，地理北向、地理東向和垂直向下為該空間坐標系的正方向，這3 個方向的分量分別記為X，Y，Z。 此外，地磁場中還有其他幾個要素：總磁場強度F，水平強度H，磁偏角D 和磁傾角I。

在這地磁場七要素中，只要知道3 個相互獨立的要素，就可以求其余的要素，它們的幾何關系為

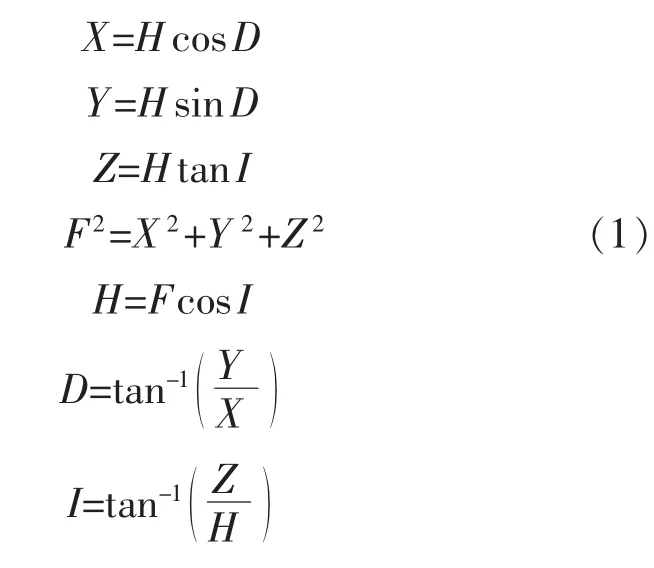
19 世紀30 年代高斯理論問世以來， 許多學者利用不同數量、不同類型的地磁資料，對地球磁場做了不同階數的球諧分析。 直到1968 年，在華盛頓召開的“地球磁場的描述”座談會上正式提出了全球地磁場模型；國際地磁學和高空物理學協會的世界地磁測量部以及協會執行委員會也先后對1965.0 國際地磁參考場給出了承認[11]。 地磁場的球諧模式即是用球諧分析法來描述地球主磁場及其長期變化的分布。

由高斯球諧分析可得，表示地磁場磁位的球諧函數為

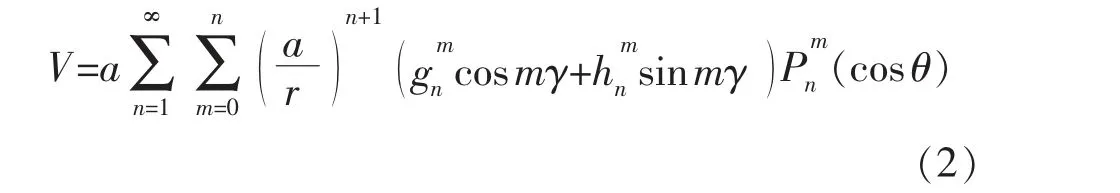
其中

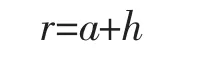
式中：a 為參考球體半徑， 通常為地球平均半徑，一般取a=6371.2 km；r 為參考球體中心至球表面或表面以上空間中的計算點的距離；h 為距離球面的高度；λ，θ 分別為球冠坐標系中的經度、緯度；，為施密特的標準化球諧系數又稱高斯系數；n 為截止階，根據最新的IGRF13 系數，截斷階數n=13，當n=m=13 時，系數總數為195 個；（cosθ）為n 階m 次的締合Legendre 函數。球冠諧系數（cosθ）的數學表達式為

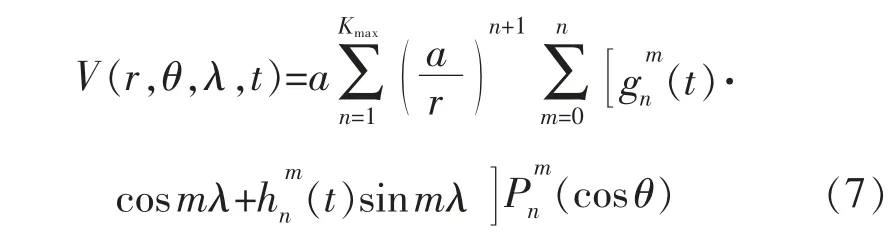
式中：Kmax為球冠諧分析的截斷階數；X，Y，Z 分別為地磁場的北向分量、東向分量和垂直分量。

根據以上公式，并結合IGRF13 的相關系數，可以得到一個自建的全球地磁場模型，并將某一個點的地理坐標、距離地面的高度數據和時間信息帶入到地磁場模型中，從而計算出地磁場的各個分量信息。

這樣，通過多次代入相關區域的坐標信息，就可以得到多個散點處的地磁分量信息。 利用這些散點信息，就可以將試驗區域內的各坐標點所對應的地磁場各分量繪制成地磁基準圖。 為了以后與地磁傳感器測量得到的實時圖進行匹配做好導航，可以把地磁基準圖預先分配一個儲存區，并將根據地磁傳感器測量得到的實時值所繪制的實時圖，在匹配算法模塊中，與預先存儲在導航系統中的地磁基準圖不斷進行匹配。 地磁基準圖生成如圖2 所示。

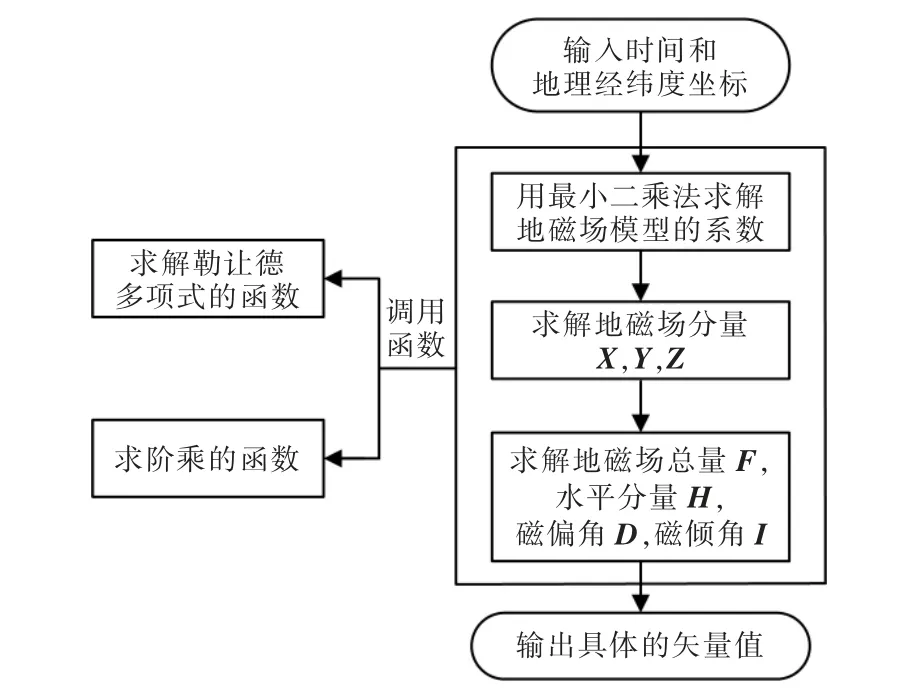
圖2 地磁基準圖計算流程Fig.2 Calculation flow chart of geomagnetic reference map

1.2 模型的準確性分析

在線WMM 2020 模型由美國國家海洋和大氣管理局（NOAA）提供，主要預測2020—2024 年5 年間地磁場主成分的變化。

在此，利用在線WMM 2020 模型數據與自建模型進行比較，分析自建模型的準確性。 2 組模型的地磁總分量F 和地向分量Z 的圖像對比如圖3，圖4所示，日期為2020 年1 月1 日，區域為經度110°E～112°E，緯度10°N～12°N，離散點間隔為0.1°，海拔0 m。

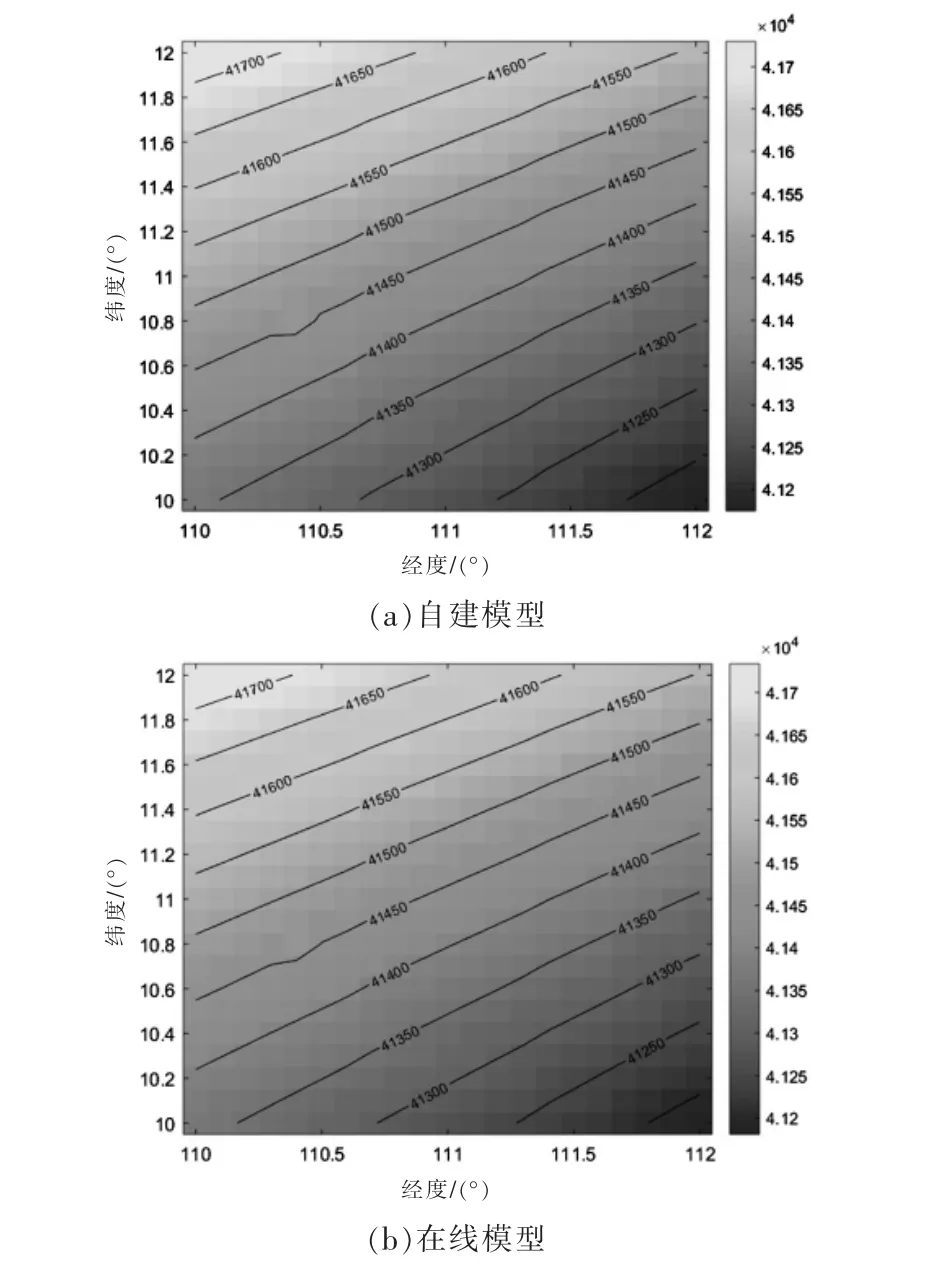
圖3 地磁總量F 分布圖Fig.3 Distribution map of total geomagnetism F

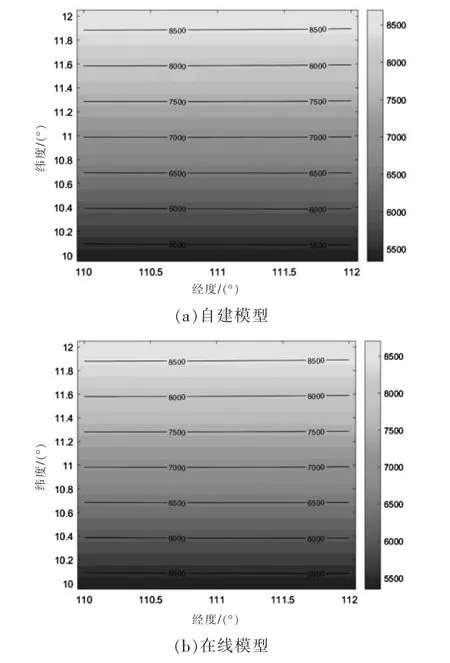
圖4 地向分量Z 分布圖Fig.4 Distribution map of ground component Z

由圖可見自建模型與在線WMM 2020 模型的仿真圖像變化趨勢較為一致。

在此從數值的角度來分析自建模型與在線WMM 2020 模型的相關性，設定以下指標作為模型準確性的參考：

1）均值 為反映數據集中趨勢的一項指標。 其計算公式為

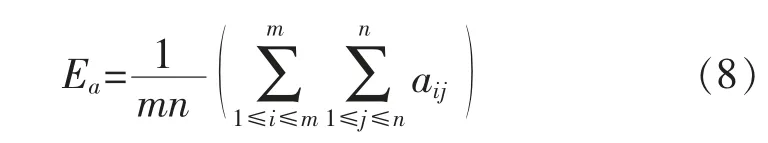
式中：aij為m×n 的矩陣A 中的值。

2）標準差 主要強調組內個體間的離散程度。其具體的計算公式為

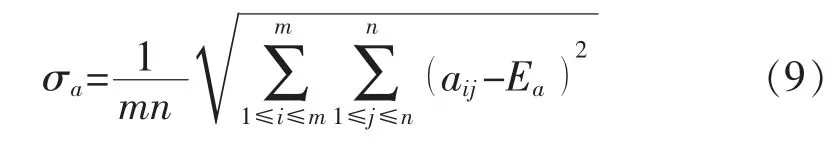
3）皮爾遜相關系數

相關系數是反映變量之間相關關系密切程度的統計指標。 著重研究線性的單相關系數，取值范圍在［-1，+1］之間。 對于相關系數的大小所表示的意義，目前在統計學界尚不一致，但通常是按表1認為的。

表1 相關系數與相關程度的關系Tab.1 Relationship between correlation coefficient and correlation degree

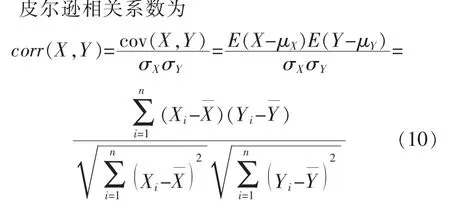
對于具有相同維度的矩陣A 和B，皮爾遜給出二維相關系數分析，計算公式為

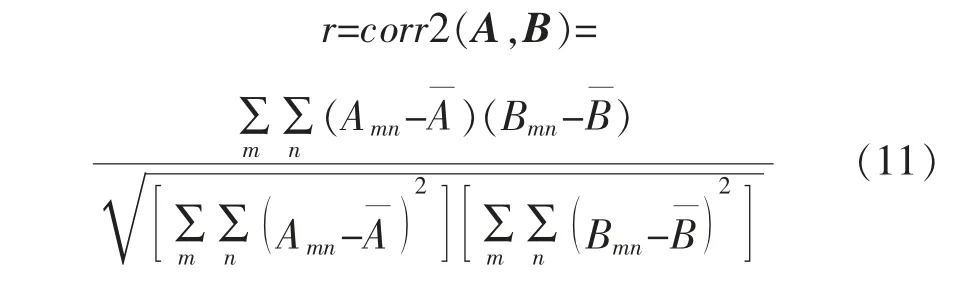
將經度110°E～112°E，緯度10°N～12°N，步長為0.1°，網格數為21×21，海拔0 m 的南海某區域的地磁場信息，與在線網站地磁計算器上的數據進行比較，以驗證自建模型的準確性。 自建模型、在線數據的均值和標準差分別見表2，表3；自建模型與在線WMM 2020 模型的相關度見表4。

表2 自建模型各分量均值和標準差Tab.2 Mean value and standard deviation of each component of self built model

表3 在線WMM 2020 各分量均值和標準差Tab.3 Mean value and standard deviation of each component of online WMM 2020

表4 自建模型與在線WMM 2020 各分量相關系數Tab.4 Correlation coefficient between self-built model and online WMM 2020

在選定的試驗區域內，相同點的各地磁分量的最小差和最大差見表5。

表5 自建模型與在線WMM 2020 模型的極差Tab.5 Range between self-built model and online WMM 2020

由表2 和表3 可知，在選定試驗區域內，自建模型與WMM 2020 模型的均值和標準差較為接近，表明自建模型與在線WMM 2020 模型在試驗區域內的分布較為一致。 由表4 可知，自建模型與在線WMM 2020 模型高度相關， 具有很強的正相關性。由表5 可知在試驗范圍內自建模型與在線WMM 2020 模型偏差較小。

為了更準確地分析自建模型與在線WMM 2020 模型的差別， 定義了均值偏差ηE和標準差偏差ησ這2 個指標。 其數值的計算方法為

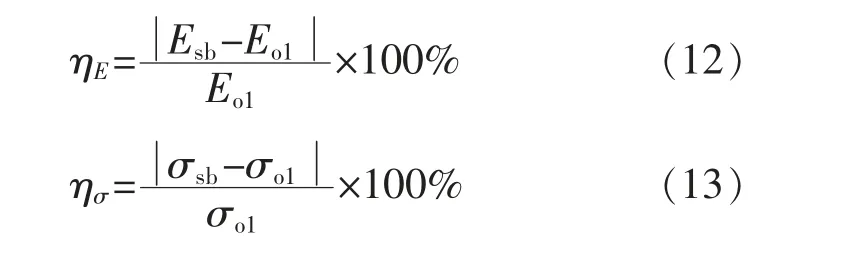
地磁各分量偏差值計算結果見表6。

表6 自建模型與在線WMM 2020 模型的均值偏差與標準差偏差Tab.6 Mean deviation and standard deviation between self-built model and online WMM 2020

由表6 可知， 以在線模型為標準作為參考，自建模型的均值和標準差與在線模型的數據相當接近；均值偏差百分比最大的地磁分量為地向分量Z，為2.346%；標準差偏差值百分比最大的地磁分量為北向分量X，為1.688%；各分量的相關系數均大于0.999，證明所選區域的自建模型與在線WMM 2020模型有很強的正相關。

綜上分析，通過圖像和數據都驗證了自建模型與在線WMM 2020 模型十分相似，從而驗證了自建模型的準確性。

2 地磁場分量分析

因為地磁基準圖的特征信息決定了后續設計地磁匹配的方法，并且特征信息對地磁匹配概率、定位精度等有關指標具有較大影響，所以需要對影響地磁基準圖匹配性能的特征信息進行綜合分析[12-13]。

在地磁匹配中，匹配特征量的選擇是指：考慮地磁場特征量在較長時間內變化的穩定程度、短期時間內變化的影響程度、地磁特征量與地理坐標位置的相關程度和相關特征，以及現有地磁傳感器的性能指標等因素，從7 個地磁場分量中選取某一個特征量或者多個特征量作為地磁基準圖匹配時特征量。

據此，在選擇匹配特征量時應重點考慮：準則1地磁特征量在較長時期內（如1a）的穩定程度；準則2地磁特征量受到短期變化（如磁暴等）的影響程度；準則3地磁特征量的變化與地理位置的相關程度；準則4地磁測量設備的測量精度；準則5匹配區域的特征信息。作為匹配準則，準則3—準則5 是進行地磁匹配的關鍵， 準則1 和準則2 是為提高地磁匹配的概率和精度而采取的細化措施。

首先，在所有的地磁特征量中，當匹配探測區域位于地磁場南北極或者地磁赤道附近時，磁偏角D 和磁傾角I 的變化才比較明顯[14-15]。根據特征量選擇的準則3 和準則4，應先排除選取磁偏角D 和磁傾角I 這2 個角度類特征量，然后從5 個強度類特征量中選取匹配特征量。

在此所選取的研究對象為位于我國南海10°～12°N，110°～120°E 的區域， 以0.1°為間隔的21×21的網格區域。 試驗數據均為海拔高為0 m 的地磁數據。 在網格區域內，分別沿西-東、南-北、西南-東北、西北-東南4 個方向，依據自建模型的相關數據計算各點的地磁分量（F，H，X，Y，Z），并進行比較分析。 在此匹配特征量的選擇結果是適用于試驗中的具體區域的。

由于數據均為相鄰變化值，為便于分析，所有數值均取其絕對值，單位為nT。 依據自建模型4 個方向相鄰坐標的地磁各分量變化情況如圖5 所示。

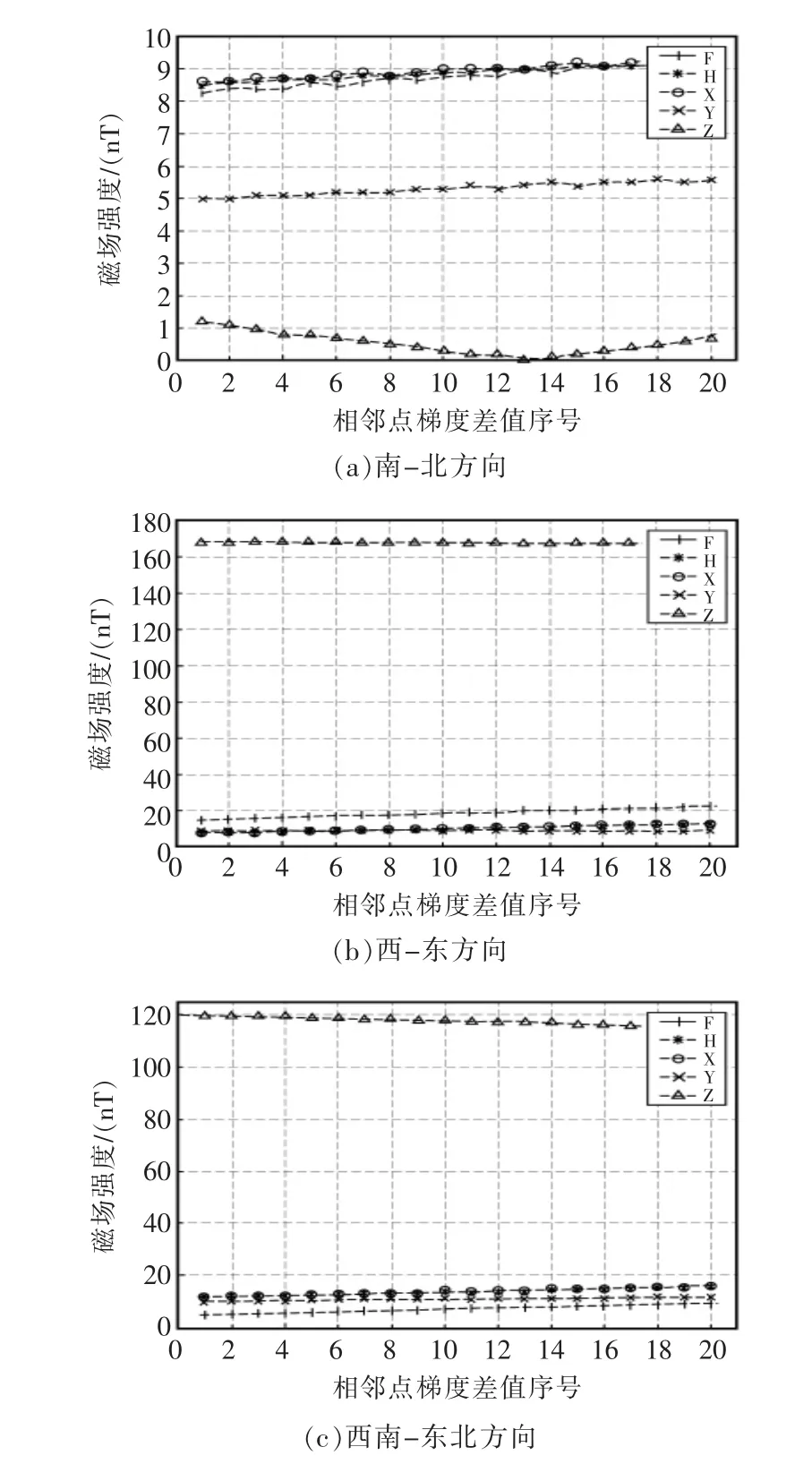
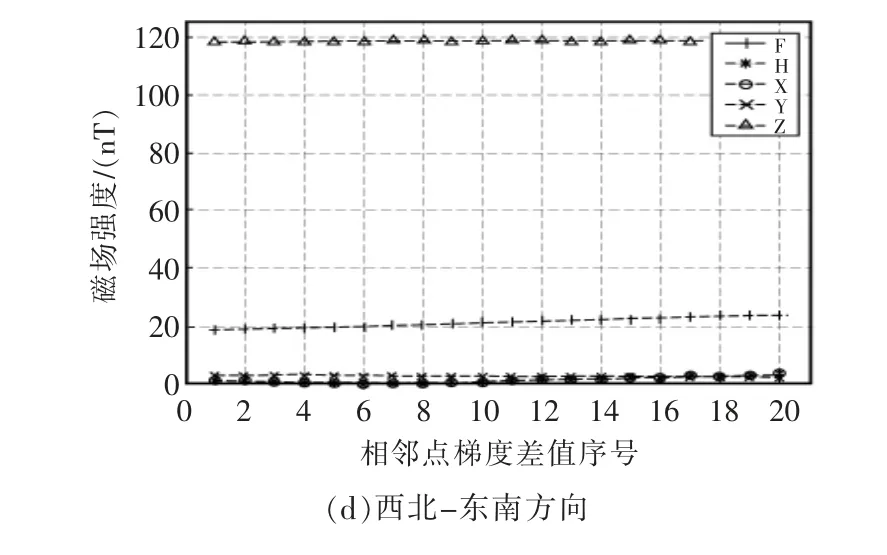
圖5 四個方向上各分量的變化Fig.5 Variation of components in four directions

由圖5 可見，在所研究的10°～12°N，110°～120°E低緯度區域內，除了在南-北方向上特征量F，H 和X 的相鄰點的地磁差值大致相同外， 在其余3 個方向上特征量Z 的相鄰點的地磁差值明顯高于其它特征量。根據特征量選取準則3，在試驗區域內可以選擇特征量Z 作為地磁匹配的特征量（接近南-北方向上，也可選擇F 作為匹配特征量）。 若將經緯度信息轉化為地理距離信息， 在10°～12°N，110°～120°E區域0.1°的間隔可粗略換算為11 km， 以Z 分量的地磁變化差值計算， 西-東方向上的地磁變化率約為16 nT/km，西南-東北和西北-東南方向上的地磁變化率約為11 nT/km，而常用的磁通門傳感器的精度為0.1 nT， 可以得知在較小范圍內Z 分量的地磁變化可以被探測到，證明了在試驗區域內選擇Z 分量作為特征量的可靠性。

經過驗證，在此所選定的區域內，以不同的經緯度間隔或者以在線WMM 2020 模型為基礎進行研究時，得到的結論依然相同。 （因篇幅有限，不再列出相關試驗數據表格和圖像）

通過分析各緯度區域的地磁數據，得出以下結論：①高緯度地區 在西-東方向上，Y 分量變化明顯；在南-北方向上，H 分量變化明顯。 ②中緯度地區 在西-東方向和南-北方向上，Z 分量變化明顯。③低緯度地區 在西-東方向上，Z 分量變化明顯；在南-北方向上，F，H 和X 分量變化較大。

3 結語

在此主要分析了地磁場模型的建立與準確度，分析了適用于地磁匹配的地磁特征量。 在分析自建模型與在線WMM 2020 模型的相似程度方面，主要引入了均值、標準差和皮爾遜相關系數3 個參考指標，定義了均值偏差量和標準值偏差量2 個指標，更深入地分析了自建模型與在線WMM 2020 模型的相似程度。 結果證明了自建模型與在線WMM 2020模型具有高度正相關性。 因此在研究地磁匹配時，將自建模型與在線WMM 2020 模型作為基本場均具可行性。 在分析適用于地磁匹配的地磁特征量時， 主要考慮了地磁場的梯度變化這一特征，分析了高、中、低緯度的地磁特征量變化，并得到初步結論。