雜波環(huán)境下強(qiáng)機(jī)動(dòng)目標(biāo)自適應(yīng)關(guān)聯(lián)波門(mén)選擇
趙 菡 諸葛晶晶 林家駿
(華東理工大學(xué)信息科學(xué)與工程學(xué)院 上海 200237)
0 引 言
關(guān)聯(lián)波門(mén)的有效設(shè)定可以減少數(shù)據(jù)關(guān)聯(lián)算法的運(yùn)算量、提高關(guān)聯(lián)精度,是數(shù)據(jù)關(guān)聯(lián)算法的必要條件[1-2],通過(guò)設(shè)置波門(mén)中心為目標(biāo)預(yù)測(cè)位置,實(shí)現(xiàn)對(duì)量測(cè)回波的篩選。概率數(shù)據(jù)關(guān)聯(lián)算法(Probabilistic Data Association, PDA)[3]以及在此基礎(chǔ)上針對(duì)多目標(biāo)優(yōu)化的聯(lián)合概率數(shù)據(jù)關(guān)聯(lián)算法(Joint Probabilistic Data Association, JPDA)[4]均是通過(guò)對(duì)波門(mén)范圍內(nèi)的所有回波計(jì)算概率進(jìn)而加權(quán)獲得目標(biāo)的狀態(tài)更新。因此,關(guān)聯(lián)波門(mén)的選取很大程度上決定了目標(biāo)的狀態(tài)更新是否精確,跟蹤是否穩(wěn)定,乃至于是否會(huì)出現(xiàn)失跟。
雜波環(huán)境下的強(qiáng)機(jī)動(dòng)目標(biāo)跟蹤存在目標(biāo)運(yùn)動(dòng)狀態(tài)變化情況復(fù)雜、波門(mén)中心難以預(yù)測(cè)等問(wèn)題,固定波門(mén)無(wú)法應(yīng)對(duì)目標(biāo)在不同狀態(tài)下的跟蹤任務(wù),因此研究者們相繼提出了多種自適應(yīng)關(guān)聯(lián)波門(mén)設(shè)計(jì)方法以改善目標(biāo)丟失問(wèn)題,提高跟蹤精度[5]。文獻(xiàn)[6]提出了一種自適應(yīng)關(guān)聯(lián)波門(mén)跟蹤算法,以目標(biāo)發(fā)生最大機(jī)動(dòng)水平作為假設(shè),修正關(guān)聯(lián)波門(mén)以增加真實(shí)回波落入概率。然而基于最大機(jī)動(dòng)水平的假設(shè)使得關(guān)聯(lián)波門(mén)過(guò)大,在雜波密集環(huán)境下反而會(huì)造成跟蹤的不穩(wěn)定甚至失跟。文獻(xiàn)[7]同樣以最大機(jī)動(dòng)水平所對(duì)應(yīng)的模型誤差協(xié)方差對(duì)關(guān)聯(lián)波門(mén)進(jìn)行擴(kuò)大,使得在波門(mén)內(nèi)不存在有效量測(cè)時(shí)擴(kuò)大波門(mén)大小以確保真實(shí)量測(cè)落入門(mén)內(nèi)。然而一味地?cái)U(kuò)大波門(mén)會(huì)造成目標(biāo)穩(wěn)定后波門(mén)內(nèi)包含過(guò)多雜波,反而影響跟蹤精確度。文獻(xiàn)[8]在誤差動(dòng)態(tài)變化率的提示下,根據(jù)目標(biāo)飛行狀態(tài)對(duì)關(guān)聯(lián)波門(mén)的大小進(jìn)行動(dòng)態(tài)調(diào)整,有效降低了目標(biāo)丟失率,提高了跟蹤精度,避免了上述算法在雜波環(huán)境下的局限。然而,該方法的研究背景是選定關(guān)聯(lián)波門(mén)的形狀為橢圓門(mén),僅存在橢圓門(mén)門(mén)限大小這一單一調(diào)節(jié)參數(shù),且在跟蹤強(qiáng)機(jī)動(dòng)目標(biāo)時(shí)門(mén)限調(diào)整幅度過(guò)小,容易出現(xiàn)失跟。文獻(xiàn)[9]采用三種波門(mén)自適應(yīng)切換的方法處理臨近空間高超聲速目標(biāo)航跡的起始問(wèn)題,一定程度上解決了上述問(wèn)題中對(duì)高機(jī)動(dòng)目標(biāo)的跟蹤問(wèn)題,但并未討論目標(biāo)持續(xù)運(yùn)動(dòng)過(guò)程中機(jī)動(dòng)變化情況下的關(guān)聯(lián)波門(mén)如何切換。
綜上,現(xiàn)有的關(guān)聯(lián)波門(mén)自適應(yīng)算法多為單一波門(mén)形狀(通常為矩形門(mén)或橢圓門(mén)),通過(guò)估計(jì)跟蹤誤差來(lái)調(diào)整門(mén)限參數(shù),實(shí)現(xiàn)波門(mén)大小的更新。該方法存在兩大缺陷:(1) 通過(guò)跟蹤誤差來(lái)調(diào)整波門(mén)門(mén)限屬于補(bǔ)救性調(diào)整,較高的滯后性導(dǎo)致波門(mén)更新不及時(shí),在目標(biāo)出現(xiàn)劇烈運(yùn)動(dòng)時(shí)容易失跟;(2) 單一形狀的矩形/橢圓門(mén)在面對(duì)雜波環(huán)境下的強(qiáng)機(jī)動(dòng)目標(biāo)時(shí),并不能很好地契合目標(biāo)運(yùn)動(dòng)狀態(tài),波門(mén)中心的劇烈變化也容易導(dǎo)致波門(mén)內(nèi)無(wú)有效量測(cè)及跟蹤不穩(wěn)定。
本文針對(duì)單一形狀波門(mén)在跟蹤強(qiáng)機(jī)動(dòng)目標(biāo)時(shí)跟蹤不穩(wěn)定及失跟嚴(yán)重的問(wèn)題,提出一種自適應(yīng)關(guān)聯(lián)波門(mén)選擇算法。通過(guò)估計(jì)當(dāng)前目標(biāo)的運(yùn)動(dòng)狀態(tài),結(jié)合目標(biāo)不確定度預(yù)測(cè)失跟概率,自適應(yīng)切換橢圓門(mén)、扇形門(mén)及環(huán)形門(mén)三種波門(mén)形狀,并動(dòng)態(tài)更新門(mén)限參數(shù)以提高波門(mén)內(nèi)正確量測(cè)的關(guān)聯(lián)概率。仿真結(jié)果表明,在強(qiáng)機(jī)動(dòng)目標(biāo)跟蹤中,本文算法可有效跟蹤目標(biāo),降低目標(biāo)丟失率的同時(shí)提升目標(biāo)的跟蹤精度。
1 自適應(yīng)參數(shù)
1.1 關(guān)聯(lián)波門(mén)
面對(duì)強(qiáng)機(jī)動(dòng)目標(biāo)的復(fù)雜運(yùn)動(dòng)狀態(tài),采用何種關(guān)聯(lián)波門(mén)進(jìn)行目標(biāo)跟蹤直接影響真實(shí)回波的落入概率,進(jìn)而影響目標(biāo)的丟失率及跟蹤精度。目前較常用的關(guān)聯(lián)波門(mén)有三種,分別為橢圓門(mén)、環(huán)形門(mén)及截尾扇形門(mén)。
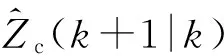
v′c(k+1)S-1(k+1)vc(k+ 1)≤γ
(1)
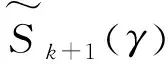
二維情況下的橢圓門(mén)面積為:
(2)
歸一化新息協(xié)方差標(biāo)準(zhǔn)差后可得橢圓門(mén)的面積為:
(3)
(2) 環(huán)形門(mén)。與橢圓門(mén)不同,環(huán)形門(mén)與方向無(wú)關(guān),能夠捕獲未知目標(biāo)或啟動(dòng)目標(biāo),其門(mén)限參數(shù)只與目標(biāo)速度相關(guān)。環(huán)形門(mén)的關(guān)聯(lián)方程如下:
(4)
式中:(x,y)為回波位置;(x1,y1)為波門(mén)中心位置;R1=f(vmin)為目標(biāo)的最小速度確定環(huán)的內(nèi)半徑;R2=f(vmax)為目標(biāo)的最大速度確定環(huán)的外半徑。
環(huán)形門(mén)的面積公式為:
(5)
(3) 截尾扇形門(mén)。截尾扇形關(guān)聯(lián)波門(mén)是扇形門(mén)的一種,本文默認(rèn)扇形門(mén)為截尾扇形門(mén),其關(guān)聯(lián)方程為:
(6)
(7)
式中:最大半徑與最小半徑的選取與環(huán)形門(mén)一致;增加角度限制于θ1~θ2,θ1、θ2由目標(biāo)的角速度所確定。
扇形門(mén)的面積公式為:
(8)
1.2 不確定度
目標(biāo)飛行過(guò)程的不確定度一定程度上反映了目標(biāo)的跟蹤穩(wěn)定性及失跟概率,當(dāng)目標(biāo)不確定度過(guò)低時(shí),說(shuō)明跟蹤極不穩(wěn)定,應(yīng)及時(shí)修正門(mén)限參數(shù)或更換波門(mén)形狀。本文通過(guò)計(jì)算目標(biāo)跟蹤不確定度,估計(jì)目標(biāo)失跟趨勢(shì),從而及時(shí)更新波門(mén)以降低失跟率。選取Hellinger距離作為衡量目標(biāo)航跡預(yù)測(cè)不確定度指標(biāo)。Hellinger距離通過(guò)評(píng)估量測(cè)向量與狀態(tài)向量?jī)蓚€(gè)分布之間的一致性來(lái)判斷目標(biāo)的關(guān)聯(lián)性能[11]。
記組合量測(cè)向量分布f=N(Zt(k),Σx),Zt(k)為組合量測(cè),Σx代表量測(cè)向量的不確定度。Zt(k)為由關(guān)聯(lián)波門(mén)確定的k時(shí)刻落入門(mén)內(nèi)的mk個(gè)有效量測(cè),其計(jì)算公式如下:
(9)

采用無(wú)偏最小方差估計(jì)迭代獲得量測(cè)向量協(xié)方差的Cramer-Rao下界[12],即不確定度Σx(k|k)。
Σx(k|k-1)=F(k-1)Σx(k-
1|k-1)F(k-1)T+Q(k-1)
(10)
Σx(k|k)=Σx(k|k-1)-K(k)S(k)K(k)T
(11)
式中:F(k)為狀態(tài)轉(zhuǎn)移矩陣;Q(k)為過(guò)程噪聲的協(xié)方差;目標(biāo)增益矩陣和新息協(xié)方差矩陣分別用K(k)和S(k)表示。
用Σx和Σy分別表示量測(cè)狀態(tài)向量x和估計(jì)狀態(tài)向量y所對(duì)應(yīng)的誤差協(xié)方差矩陣,則Hellinger距離dKG(k)為:
(12)
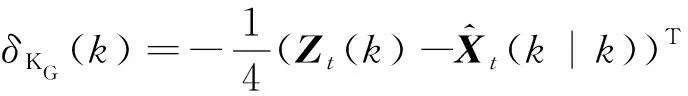
(13)
2 算法設(shè)計(jì)
2.1 選擇原理
在實(shí)際應(yīng)用中,不同場(chǎng)景下采用的關(guān)聯(lián)波門(mén)應(yīng)根據(jù)實(shí)際情況調(diào)整。面對(duì)初始捕獲階段的眾多自由點(diǎn)跡,需采用較大的無(wú)方向性波門(mén),環(huán)形門(mén)是一個(gè)合適的選擇。跟蹤開(kāi)始后,對(duì)于不同的跟蹤目標(biāo)通常有不同的波門(mén)選擇策略。例如,在民用航空雷達(dá)應(yīng)用中,民航機(jī)一般不會(huì)進(jìn)行較大幅度的機(jī)動(dòng),因此,選擇一個(gè)較小的波門(mén)即可,可以采用橢圓門(mén),對(duì)一個(gè)速度穩(wěn)定,方向變化小的目標(biāo)進(jìn)行跟蹤。而在軍用領(lǐng)域,由于戰(zhàn)斗機(jī)往往速度較快,且頻繁地進(jìn)行緊急避讓、急轉(zhuǎn)、加速、減速等強(qiáng)機(jī)動(dòng)變化,因此該場(chǎng)景下往往需要一個(gè)較大的波門(mén)(扇形波門(mén)/環(huán)形門(mén))以涵蓋可能出現(xiàn)的速度及方向變化。
盡管波門(mén)越大,越容易捕獲真實(shí)目標(biāo)回波,但與此同時(shí),也會(huì)有較多來(lái)自非本目標(biāo)的回波及雜波落入波門(mén);反之,波門(mén)選取過(guò)小,會(huì)使來(lái)自本目標(biāo)的回波被排除在外,產(chǎn)生不穩(wěn)定的跟蹤,甚至使得跟蹤目標(biāo)丟失。因此,需要根據(jù)實(shí)際情況選取恰當(dāng)?shù)牟ㄩT(mén),即不可盲目增大波門(mén),也需要使波門(mén)大小在一定限度之內(nèi),確保目標(biāo)真實(shí)回波在波門(mén)外的概率小于一定程度。
本文所采用的橢圓門(mén)、扇形門(mén)及環(huán)形門(mén)示意圖如圖1所示。
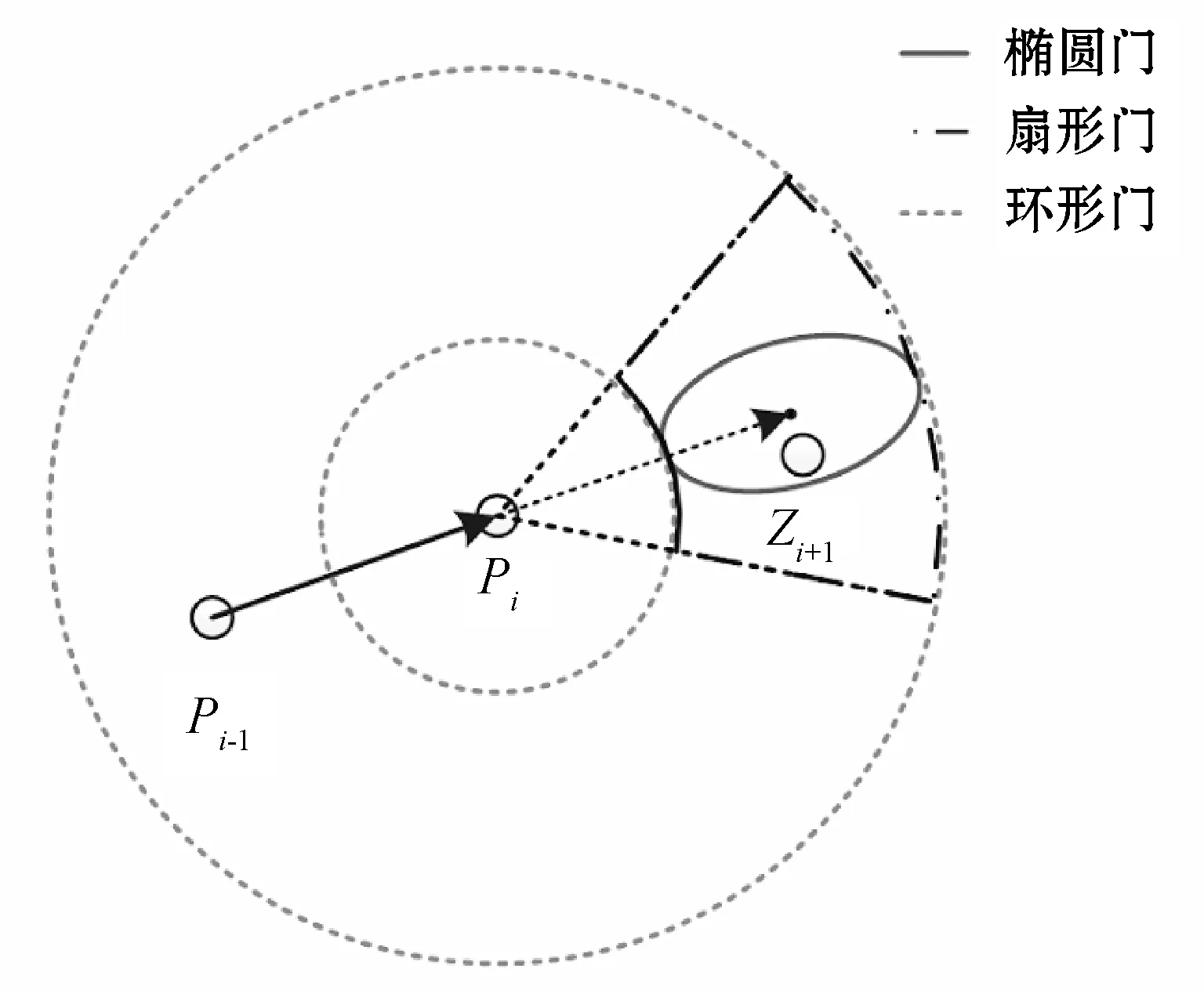
圖1 關(guān)聯(lián)波門(mén)示意圖
圖中,Pi-1為上一時(shí)刻預(yù)測(cè)點(diǎn)跡,Pi為當(dāng)前時(shí)刻預(yù)測(cè)點(diǎn)跡,Zi+1為下一時(shí)刻的量測(cè)點(diǎn)跡。合適的波門(mén)應(yīng)該在各種情況下都能涵蓋Zi+1點(diǎn)。可以看出:橢圓門(mén)面積最小,但方向性最佳,適用于小機(jī)動(dòng)情況,可有效減少波門(mén)內(nèi)所包含的雜波;扇形波門(mén)面積次之,具有一定方向性,適用于大機(jī)動(dòng)情況;環(huán)形門(mén)無(wú)方向性,波門(mén)面積最大,適用于目標(biāo)啟動(dòng)狀態(tài)及失跟時(shí)用于重新捕獲目標(biāo)。
2.2 選擇流程
自適應(yīng)波門(mén)決策主要是根據(jù)當(dāng)前波門(mén)內(nèi)的有效量測(cè)來(lái)選擇對(duì)應(yīng)波門(mén)。如前文所述,橢圓門(mén)適用于弱機(jī)動(dòng)環(huán)境,扇形波門(mén)適用于角度變化在一定范圍內(nèi)的機(jī)動(dòng)目標(biāo),環(huán)形門(mén)適用于目標(biāo)丟失需重新捕獲的情況。考慮單一形狀波門(mén)無(wú)法應(yīng)對(duì)復(fù)雜的機(jī)動(dòng)環(huán)境,現(xiàn)提出一種自適應(yīng)波門(mén)決策算法,針對(duì)不同的機(jī)動(dòng)環(huán)境下的跟蹤目標(biāo)選擇最合適的波門(mén)形狀。在目標(biāo)實(shí)際航行過(guò)程中,通過(guò)估計(jì)目標(biāo)運(yùn)動(dòng)狀態(tài)以及判斷波門(mén)內(nèi)有無(wú)有效回波來(lái)決定是否更換波門(mén),具體的決策過(guò)程如下:
首先預(yù)測(cè)當(dāng)前目標(biāo)運(yùn)動(dòng)狀態(tài),當(dāng)在波門(mén)內(nèi)尋找到有效量測(cè),根據(jù)數(shù)據(jù)關(guān)聯(lián)算法得到當(dāng)前目標(biāo)預(yù)測(cè)速度vP(k)為:
(14)
式中:k為當(dāng)前時(shí)刻;XP為預(yù)測(cè)的航跡;t為量測(cè)間隔時(shí)間。
定義δ為表示目標(biāo)觸發(fā)啟動(dòng)狀態(tài)的閾值,θ為根據(jù)工程經(jīng)驗(yàn)選取的閾值。當(dāng)vP(k)<δ時(shí),認(rèn)為目標(biāo)處于啟動(dòng)狀態(tài),則采用內(nèi)半徑為0,外半徑為初始設(shè)定最大速度Vmax的環(huán)形門(mén)(圓形門(mén)),尋找起始航跡。
當(dāng)目標(biāo)|vP(k)-vP(k-1)|<δ且|atan2(vP(k))-atan2(vP(k-1))|<θ時(shí),認(rèn)為目標(biāo)接近于勻速直線運(yùn)動(dòng)狀態(tài):更換橢圓門(mén)對(duì)目標(biāo)進(jìn)行跟蹤。
當(dāng)目標(biāo)|atan2(vP(k))-atan2(vP(k-1))|>θ時(shí),認(rèn)為目標(biāo)處于轉(zhuǎn)彎?rùn)C(jī)動(dòng)狀態(tài),則更換扇形門(mén)對(duì)目標(biāo)進(jìn)行跟蹤。
當(dāng)波門(mén)內(nèi)不存在有效量測(cè)或不確定度過(guò)大時(shí),認(rèn)為目標(biāo)已丟失,采用默認(rèn)環(huán)形門(mén)重新確定目標(biāo)航跡。
此外,算法根據(jù)當(dāng)前運(yùn)動(dòng)狀態(tài)實(shí)時(shí)更新三種波門(mén)門(mén)限參數(shù),以降低雜波落入的概率,提高真實(shí)回波在波門(mén)內(nèi)的關(guān)聯(lián)概率。波門(mén)門(mén)限的更新規(guī)則如下:
環(huán)形門(mén)門(mén)限參數(shù)更新規(guī)則:最小速度為max(vP-aline·t-δ,0),最大速度為vP+aline·t+δ。其中aline由跟蹤目標(biāo)最大線加速度所決定,留有一定的余量以防止受量測(cè)誤差及預(yù)測(cè)誤差影響而超出上下邊界。
扇形門(mén)門(mén)限參數(shù)更新規(guī)則:最小速度與最大速度的設(shè)定與環(huán)形門(mén)一致。扇形門(mén)的順時(shí)針轉(zhuǎn)角與逆時(shí)針轉(zhuǎn)角邊界為±(αθ×atan2(vP(k))-atan2(vP(k-1))+δ)。其中αθ由跟蹤目標(biāo)最大角加速度所決定。
自適應(yīng)關(guān)聯(lián)波門(mén)決策算法流程如圖2所示。

圖2 自適應(yīng)關(guān)聯(lián)波門(mén)決策算法流程圖
3 實(shí) 驗(yàn)
3.1 性能指標(biāo)
本文采用兩種機(jī)動(dòng)目標(biāo)跟蹤性能評(píng)估指標(biāo)衡量跟蹤狀態(tài)的穩(wěn)定性及跟蹤精度。采用真實(shí)回波關(guān)聯(lián)概率衡量跟蹤算法穩(wěn)定性[13]。假設(shè)系統(tǒng)的狀態(tài)和噪聲g(k)均表現(xiàn)為高斯過(guò)程,則新息向量也是高斯過(guò)程,并且g(k)服從自由度為M的χ2分布。新息向量v(k)的高斯概率密度函數(shù)為:
(15)
式中:|S(k)|為新息向量協(xié)方差矩陣的行列式;M為觀測(cè)維數(shù),本文取M=2。
對(duì)于PDA算法而言,過(guò)大的門(mén)限將引入過(guò)多的雜波,而PDA算法將每一個(gè)雜波都納入最終目標(biāo)狀態(tài)預(yù)測(cè)的計(jì)算中,過(guò)多的雜波在導(dǎo)致算法計(jì)算量增大的同時(shí)降低了正確回波的關(guān)聯(lián)概率,從而影響目標(biāo)狀態(tài)的預(yù)測(cè)精度。相反,門(mén)限過(guò)小則增加了波門(mén)內(nèi)丟失正確回波的概率。若波門(mén)內(nèi)檢測(cè)不到觀測(cè)回波,在持續(xù)數(shù)個(gè)觀測(cè)周期后算法將停止跟蹤該目標(biāo),進(jìn)而造成目標(biāo)航跡的不連續(xù),甚至目標(biāo)的丟失。根據(jù)PDA算法定義,目標(biāo)狀態(tài)的更新由波門(mén)內(nèi)所包含的各個(gè)回波各自加權(quán)后的和所決定。由此,可以定義波門(mén)內(nèi)正確回波的歸一化關(guān)聯(lián)概率大小來(lái)表征門(mén)限決策算法的性能,具體數(shù)學(xué)表達(dá)式如下:
(16)
式中:第k個(gè)掃描周期內(nèi)落入關(guān)聯(lián)波門(mén)內(nèi)的回波點(diǎn)跡總數(shù)為mk;vc(k)表示正確回波的新息向量。當(dāng)正確回波均未落入關(guān)聯(lián)波門(mén)時(shí),其對(duì)應(yīng)的歸一化關(guān)聯(lián)概率ωc的大小為0;若落入關(guān)聯(lián)波門(mén)內(nèi)的僅有正確回波,則ωc的大小為1,此時(shí)門(mén)限決策算法的性能最為優(yōu)異。
計(jì)算真實(shí)航跡與預(yù)測(cè)航跡間的歐式距離誤差,即位置均方根誤差評(píng)估跟蹤精度,具體計(jì)算公式如下:
(17)

3.2 仿真實(shí)驗(yàn)設(shè)定
設(shè)置目標(biāo)檢測(cè)概率,量測(cè)落入關(guān)聯(lián)波門(mén)內(nèi)的概率,雜波均勻分布在以正確量測(cè)為中心的正方形區(qū)域內(nèi),雜波密度為106 個(gè)/m2。對(duì)于三種候選波門(mén),初始橢圓門(mén)門(mén)限常數(shù)為9.21,環(huán)形門(mén)與扇形門(mén)最小速度參數(shù)(最小半徑)為0,最大速度為80 m/s,此外,扇形門(mén)最大偏轉(zhuǎn)角為1.21 rad。
構(gòu)建目標(biāo)運(yùn)動(dòng)過(guò)程如下:目標(biāo)初始位置位于[0,0]處,初始速度為0 m/s;1~10 s內(nèi)目標(biāo)做固定加速度為15 m/s2的勻加速直線運(yùn)動(dòng);11~40 s內(nèi)做勻速直線運(yùn)動(dòng);41~50 s內(nèi)向目標(biāo)右前方做角加速度為11.46 rad/s2的轉(zhuǎn)彎?rùn)C(jī)動(dòng);51~70 s繼續(xù)勻速直線運(yùn)動(dòng);71~80 s做加速度為20 m/s2的勻加速直線運(yùn)動(dòng)。
3.3 實(shí)驗(yàn)結(jié)果分析
目標(biāo)運(yùn)動(dòng)狀態(tài)如圖3所示。圖中標(biāo)記了實(shí)驗(yàn)仿真過(guò)程中各波門(mén)的切換情況,在啟動(dòng)狀態(tài)時(shí),采用無(wú)方向性的環(huán)形門(mén)進(jìn)行跟蹤;待運(yùn)動(dòng)狀態(tài)穩(wěn)定,目標(biāo)處于近乎勻速直線運(yùn)動(dòng)時(shí)采用誤差最小的橢圓門(mén)進(jìn)行跟蹤;當(dāng)目標(biāo)處于拐彎?rùn)C(jī)動(dòng)或加速狀態(tài)時(shí),采用扇形門(mén)進(jìn)行跟蹤。出現(xiàn)跟蹤不穩(wěn)定時(shí),重新更換環(huán)形門(mén)進(jìn)行跟蹤。
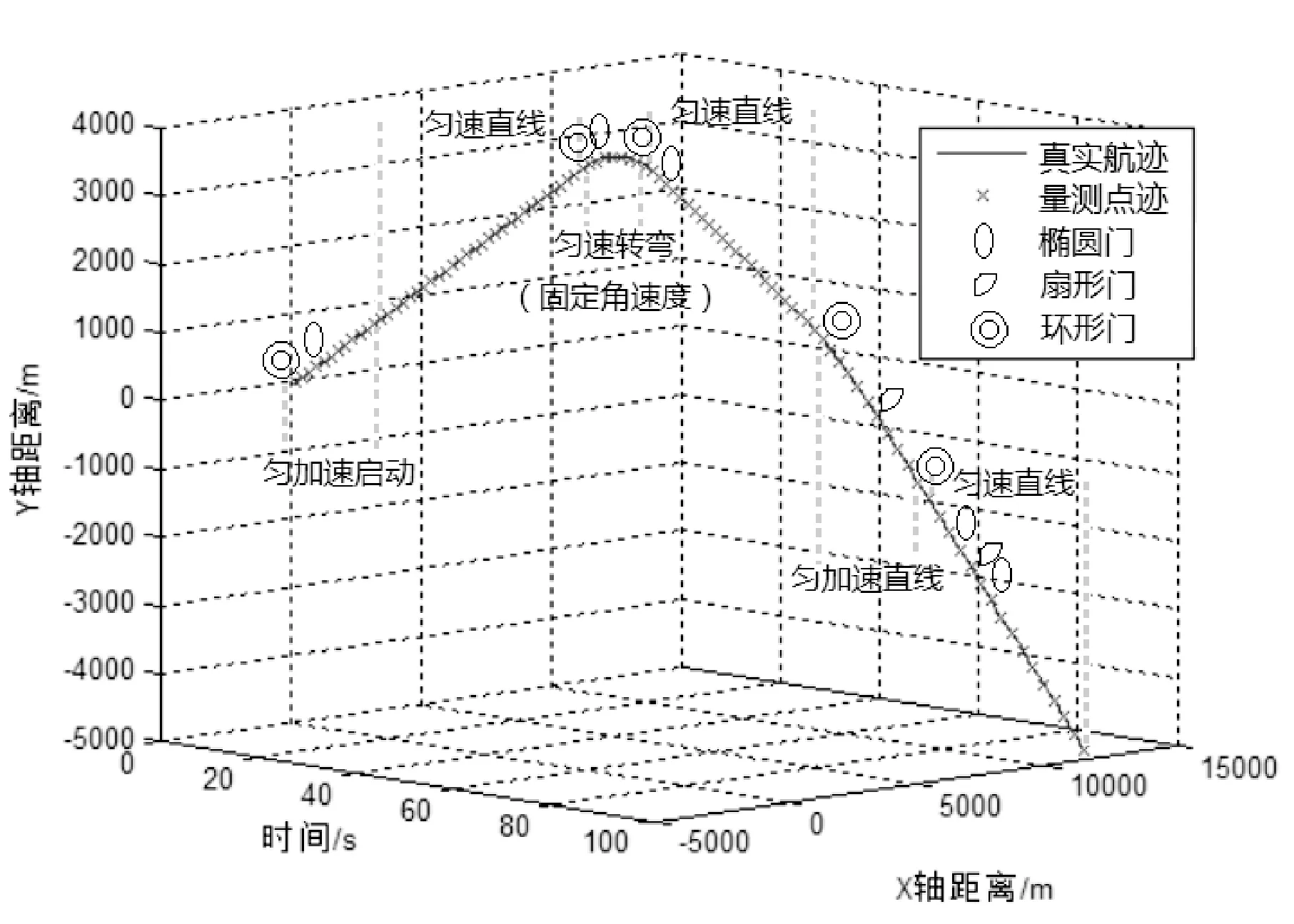
圖3 目標(biāo)航跡與波門(mén)切換
表1展示了波門(mén)切換情況。初始啟動(dòng)狀態(tài),采用了環(huán)形門(mén),待目標(biāo)穩(wěn)定后,3 s開(kāi)始采用橢圓門(mén),當(dāng)目標(biāo)出現(xiàn)不穩(wěn)定時(shí),重新切換至環(huán)形門(mén);44 s時(shí)檢測(cè)到轉(zhuǎn)彎?rùn)C(jī)動(dòng),切換至扇形門(mén)。51 s重新采用環(huán)形門(mén),待穩(wěn)定后54 s開(kāi)始采用橢圓門(mén)跟蹤;75 s時(shí)目標(biāo)處于加速狀態(tài),橢圓門(mén)無(wú)法跟上目標(biāo),采用環(huán)形門(mén),確定方向后,切換至扇形門(mén),直至檢測(cè)到勻速后,83 s切換至橢圓門(mén)。隨著目標(biāo)的速度逐漸增大,切換至環(huán)形門(mén)、扇形門(mén)的幾率也逐漸增多。目標(biāo)跟蹤過(guò)程的波門(mén)切換符合實(shí)際,切換過(guò)程合理。
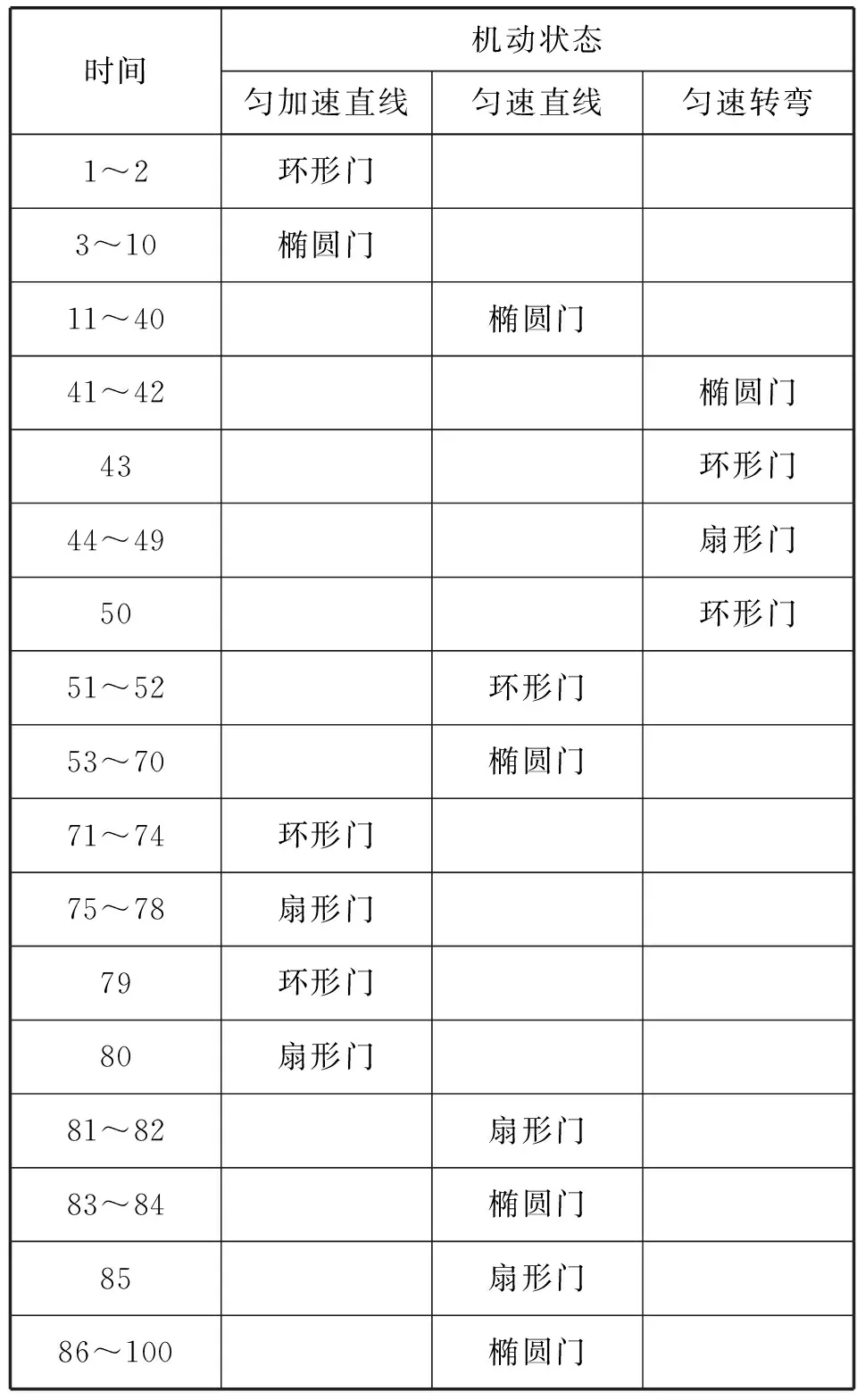
表1 波門(mén)切換
圖4展示了固定波門(mén)與本文算法在同樣場(chǎng)景下的跟蹤情況比較。起始位置處,由于扇形門(mén)是帶方向性波門(mén),對(duì)初始速度為0的目標(biāo),一旦初始方向未落在扇形門(mén)內(nèi)即無(wú)法跟蹤。橢圓門(mén)則在轉(zhuǎn)彎?rùn)C(jī)動(dòng)處丟失目標(biāo),環(huán)形門(mén)在目標(biāo)速度超出其初始設(shè)定值時(shí)發(fā)生丟失,而自適應(yīng)波門(mén)則能根據(jù)目標(biāo)當(dāng)前運(yùn)動(dòng)狀態(tài)自動(dòng)切換。此外,扇形門(mén)及環(huán)形門(mén)的上下限速度及方向也能根據(jù)當(dāng)前運(yùn)動(dòng)狀態(tài)進(jìn)行合理的自適應(yīng)調(diào)整,因此能有效跟蹤強(qiáng)機(jī)動(dòng)狀態(tài)下的目標(biāo)。

(a) 固定波門(mén)跟蹤軌跡

(b) 自適應(yīng)波門(mén)跟蹤軌跡圖4 波門(mén)跟蹤軌跡比較
圖5展示了采用固定波門(mén)與自適應(yīng)波門(mén)真實(shí)回波關(guān)聯(lián)概率的對(duì)比:相比固定波門(mén)的不穩(wěn)定性,自適應(yīng)波門(mén)在勻速運(yùn)動(dòng)狀態(tài)下均保持了較高的關(guān)聯(lián)概率,僅在初始啟動(dòng)時(shí)刻、轉(zhuǎn)彎?rùn)C(jī)動(dòng)及加速時(shí)產(chǎn)生一定的下降。
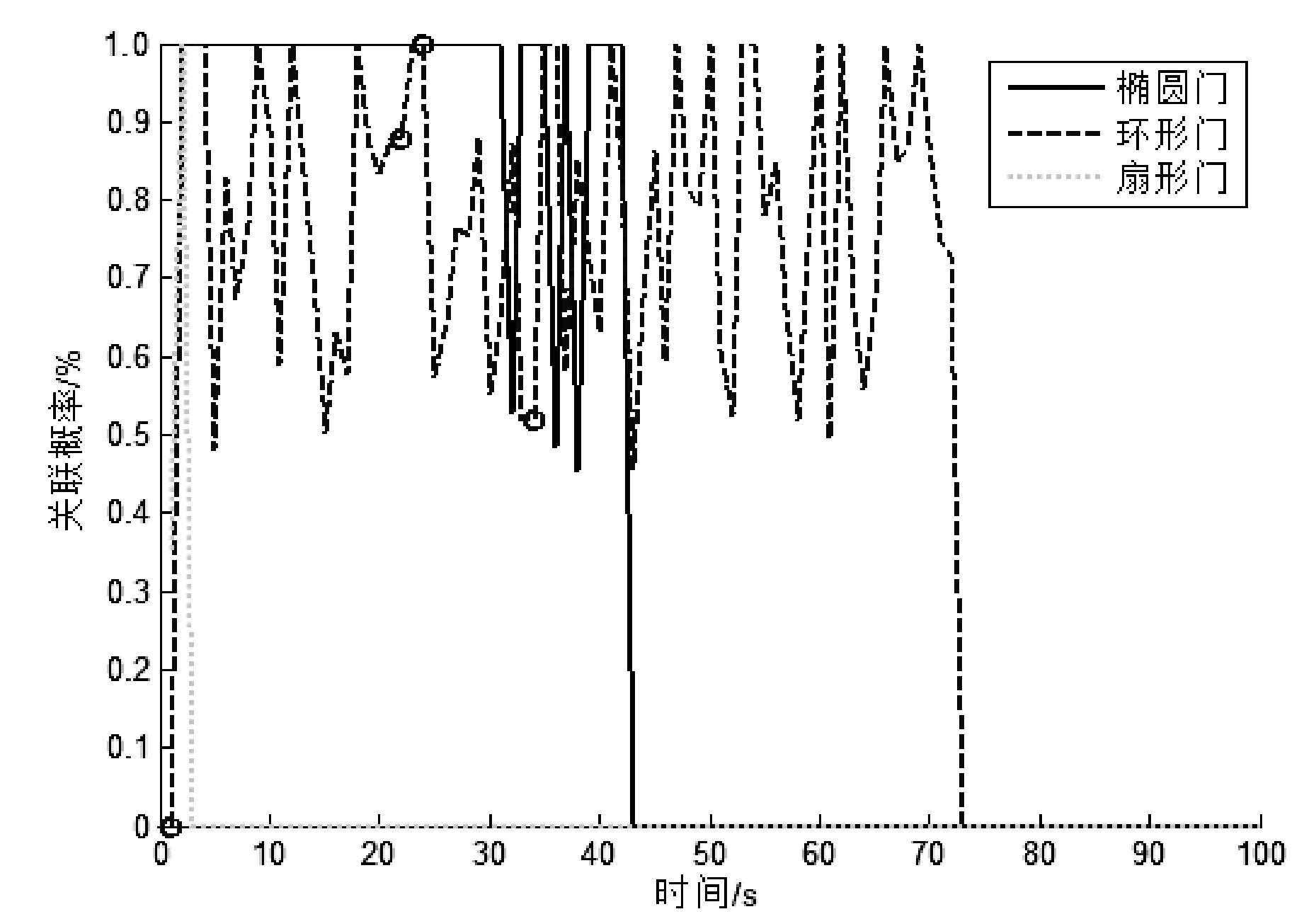
(a) 固定波門(mén)關(guān)聯(lián)概率
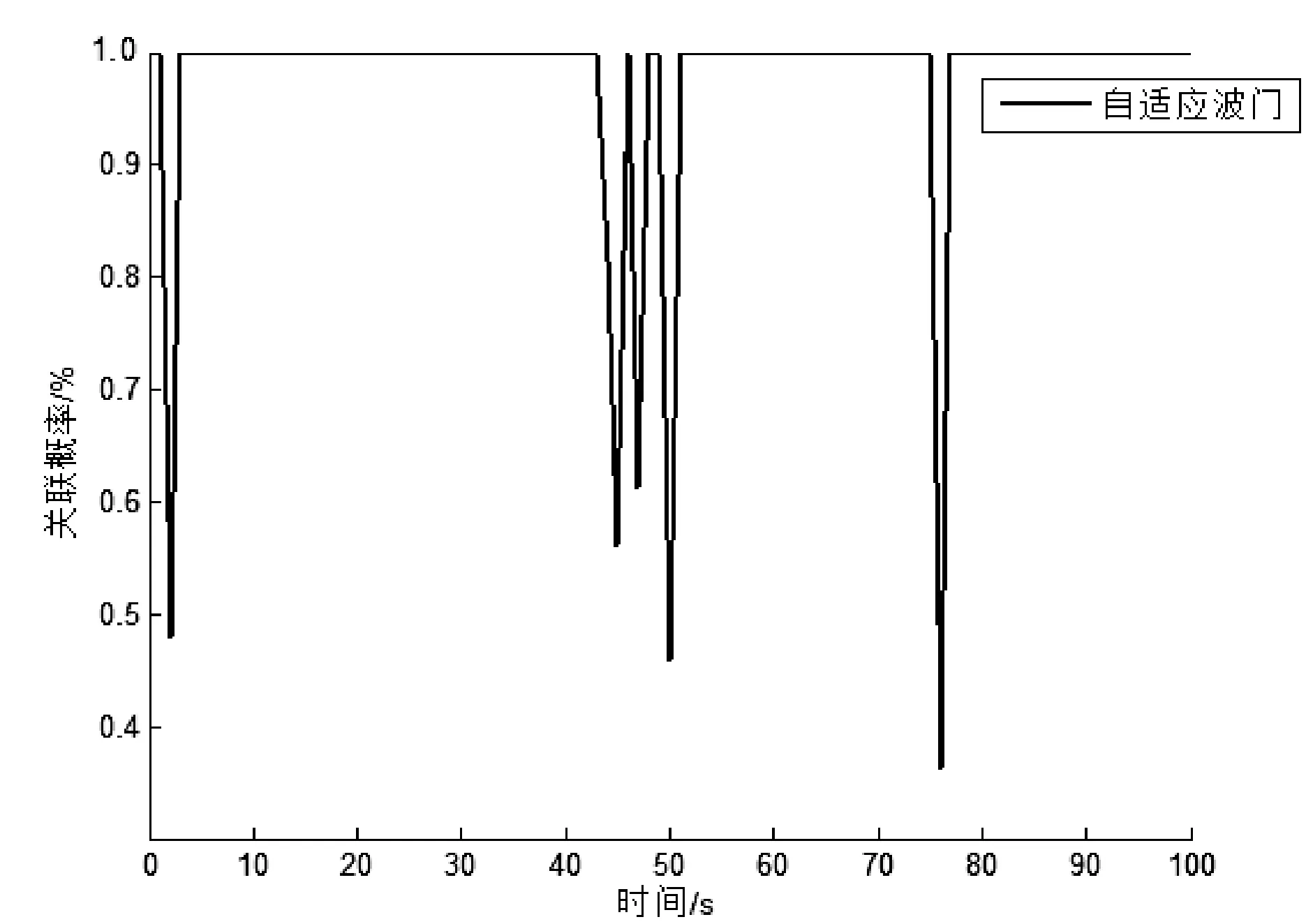
(b) 自適應(yīng)波門(mén)關(guān)聯(lián)概率圖5 波門(mén)關(guān)聯(lián)概率比較
圖6比較了固定波門(mén)與本文提出的自適應(yīng)波門(mén)在跟蹤精度上的性能。排除固定波門(mén)失跟情況,在跟蹤過(guò)程中,本文提出的自適應(yīng)波門(mén)在跟蹤距離誤差上亦表現(xiàn)出了較大程度的下降。在啟動(dòng)環(huán)節(jié)及勻速運(yùn)動(dòng)環(huán)節(jié)中,本文算法將距離誤差保持在4 m以下,而在轉(zhuǎn)彎與加速機(jī)動(dòng)過(guò)程中,距離誤差也保持在12 m以下。
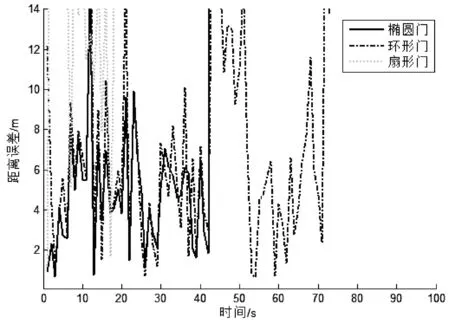
(a) 固定波門(mén)距離誤差
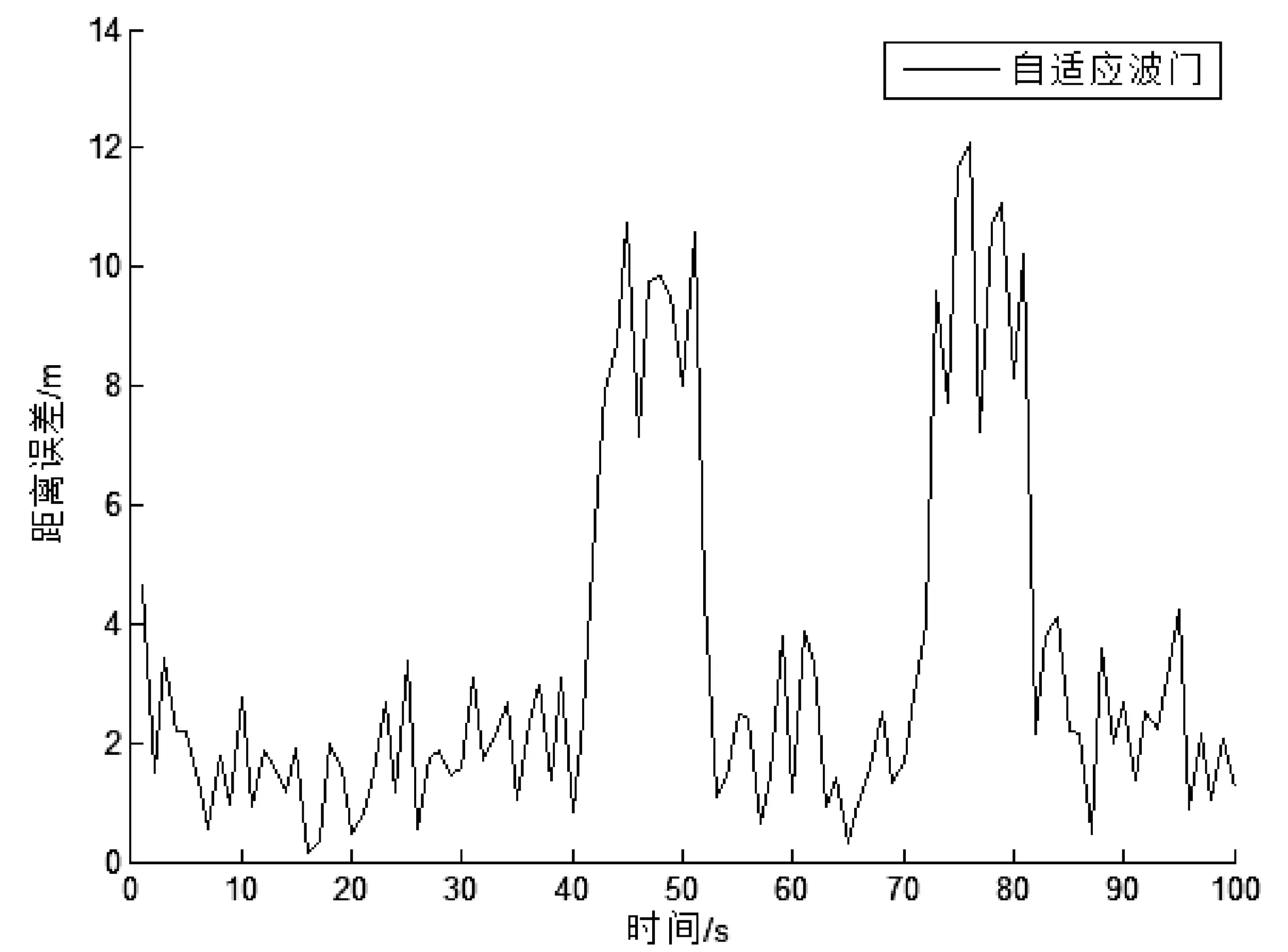
(b) 自適應(yīng)波門(mén)距離誤差圖6 波門(mén)跟蹤距離誤差比較
此外,實(shí)驗(yàn)?zāi)M不同雜波密度下對(duì)強(qiáng)機(jī)動(dòng)目標(biāo)跟蹤性能的影響,并與文獻(xiàn)[8]中的傳統(tǒng)自適應(yīng)關(guān)聯(lián)波門(mén)算法進(jìn)行了比較。比較結(jié)果如表2所示。
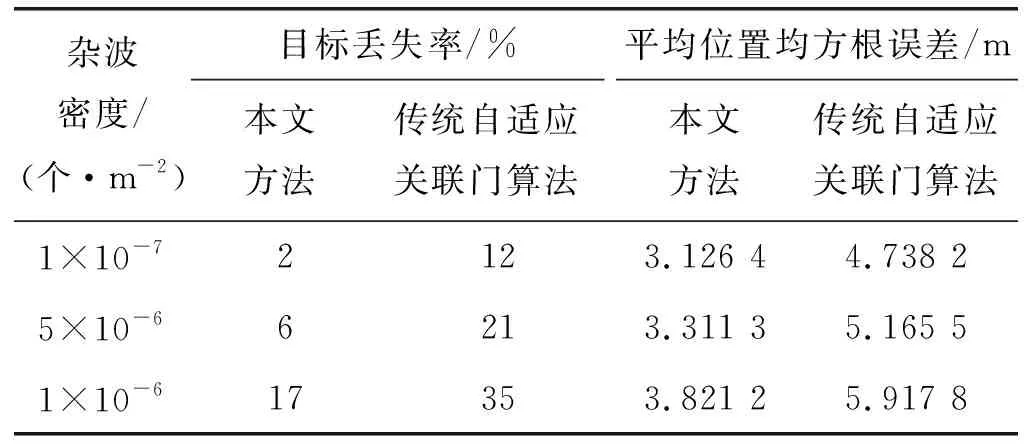
表2 不同雜波密度下兩種方法的跟蹤性能比較
可以看出,相比文獻(xiàn)[8]中的自適應(yīng)關(guān)聯(lián)波門(mén)算法,本文算法在各雜波密度下均呈現(xiàn)出更低的目標(biāo)丟失率及位置均方根誤差,平均目標(biāo)丟失率下降約15%,平均位置均方根誤差下降約35%。
4 結(jié) 語(yǔ)
在面對(duì)雜波環(huán)境下的強(qiáng)機(jī)動(dòng)目標(biāo)跟蹤問(wèn)題時(shí),固定關(guān)聯(lián)波門(mén)并不能完全契合所有的目標(biāo)機(jī)動(dòng)狀態(tài),容易出現(xiàn)斷跟或失跟現(xiàn)象。而傳統(tǒng)的自適應(yīng)關(guān)聯(lián)波門(mén)設(shè)計(jì)多采用單一波門(mén)形狀,在面對(duì)機(jī)動(dòng)狀態(tài)急劇變化且多樣的目標(biāo)時(shí),容易出現(xiàn)跟蹤不穩(wěn)定乃至丟失目標(biāo)的問(wèn)題。本文設(shè)計(jì)了自適應(yīng)波門(mén)決策算法,根據(jù)目標(biāo)當(dāng)前運(yùn)動(dòng)狀態(tài),通過(guò)動(dòng)態(tài)切換橢圓門(mén)、扇形門(mén)及環(huán)形門(mén),達(dá)到在面對(duì)不同的機(jī)動(dòng)狀態(tài)選擇最佳波門(mén)形狀,予以參與后續(xù)關(guān)聯(lián)算法估計(jì)目標(biāo)位置。在更新目標(biāo)運(yùn)動(dòng)狀態(tài)的同時(shí),同步更新波門(mén)門(mén)限參數(shù)以減少波門(mén)內(nèi)雜波數(shù)量。而當(dāng)目標(biāo)不確定度過(guò)大,預(yù)計(jì)出現(xiàn)失跟時(shí),選擇環(huán)形門(mén)以重新捕獲目標(biāo),降低目標(biāo)丟失率。實(shí)驗(yàn)結(jié)果表明,在不同雜波環(huán)境及不同的機(jī)動(dòng)狀態(tài)下,相比固定波門(mén)及傳統(tǒng)自適應(yīng)波門(mén),本文算法都在保持較低的目標(biāo)丟失率的同時(shí)獲得了較高的跟蹤精度。

