導函數的零點不可求怎么辦?
◎張運能
在導數大題的求解或證明中,很多時候需要求解函數或者導函數的零點,學生對于處理函數零點可求時可能較為熟練,但在面對函數的零點不可求或零點不存在情形等問題時,就手足無措,無從下手了。我們是否就是"束手無策"呢?顯然不是!對于這一類問題的求解,可從以下三方面入手解決。
一、猜根:通過觀察方程的結構特征,猜出方程f′(x)=0 的根
對于有關x 與ln x 的組合函數為背景的試題,要求學生理解導數公式和導數的運算法則等基礎知識,準確的求出函數的導數,當所求的導函數解析式中出現lnx時,常猜x=1;當函數解析式中出現ex時,常猜x=0,然后代入未知數x 的值進行檢驗,看看滿足方程f′(x)=0 嗎?
(1)若函數f(x)在(a,a+1)上有極值,求實數a 的取值范圍;
(2)若關于x 的方程f(x)=x2-2x+k有實數解,求實數k 的取值范圍.
(2)由已知可得,方程f(x)=x2-2x+k 有實數根,
即f(x)-x2+2x=k 有實數根.
設g(x)=f(x)-x2+2x,
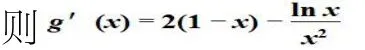
接下來,需求函數g(x)的單調區間,所以需解不等式g′(x)≥0 及g′(x)≤0,因而需解方程g′(x)=0。但此方程不易求解,所以我們可以先猜后解.
因為g′(1)=0,且當0<x<1 時,g′(x)>0,當x>1 時,g′(x)<0,所以函數g(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減
所以g(x)max=g(1)=3/2。當x→0時,g(x)→-∞;當x→+∞時,g(x)→-∞,所以函數g(x)的值域是(-∞,3/2),所以所求實數k 的取值范圍是(-∞,3/2)。
對于這種猜想方程的根的方法,有時可以減少很多解方程的運算過程,從而提高解題速度,但學生往往不太敢用或者不習慣用,在教學中需要老師主動引導,積極培養。
二、設根:通過運算代換、數值估計,虛設f′(x)=0 的根
有這么一類試題,導函數的零點無法求解,但我們能判斷零點是存在的,我們可以把這一類問題形象地稱作“隱零點問題”。這個零點就是我們所說的“隱零點”,它是客觀存在的,但是又不那么好找,對于這一類問題的求解,往往可以采用“虛設零點、整體代換”的方法,雖然不能求解導函數的零點,但我們可以假設零點是x0,這種方法稱為“虛設零點法”,于是就有f′(x0)=0。而在進一步的問題求解中,我們經常會遇見一些較為復雜的函數式,例如指數式與對數式、冪函數式等的混合,這時我們可以利用f′(x0)=0 來代換,將超越式(指數式、對數式等)替換成簡單易于求解的函數式,進而求解相關問題。
例題2.已知函數f(x)=aex-bln x,曲線y=f(x)在點(1,f(1))處的切線方程為
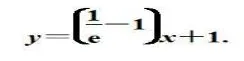
(1)求a,b;
(2)證明:f(x)>0。
解:(1)函數f(x)的定義域為(0,+∞).
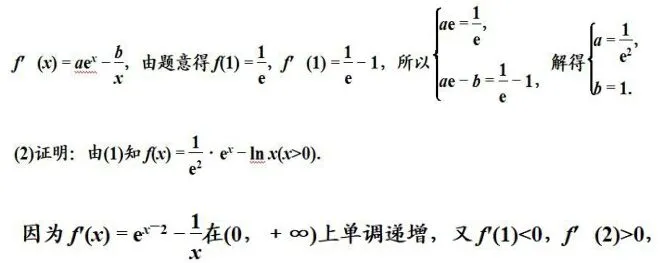
所以f′(x)=0 在(0,+∞)上有唯一實根x0,且x0∈(1,2).
當x∈(0,x0)時,f′(x)<0,當x∈(x0,+∞)時,f′(x)>0,
從而當x=x0時,f(x)取極小值,也是最小值.

則x0-2=-ln x0
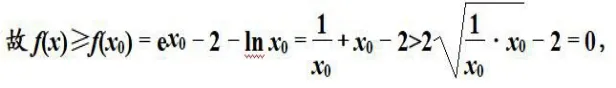
所以f(x)>0。
諸如此類的例題有很多,同學們要學會應用。“虛設零點法”常用到的解題技巧主要可以歸納為以下幾點:(1)整體代換,將超越式轉化為普通式。利用這類技巧,可以通過逐步分析零點所在區間以及滿足的關系討論函數的單調性,最后利用零點所滿足的恒等關系整體代入,將函數關系轉化為普通式。(2)反代消參,構造關于零點的單一函數。如果問題要求解的結論與參數無關,這時一般不要用參數來表示零點,而是反過來用零點表示參數,然后把極值函數變成關于零點的單一函數再進行求解。(3)降次留參,建立含參數的方程或不等式。如果問題要求解的結論與參數有關,可利用導數為零的方程,在保留參數的情況下,不斷把零點的次數降到不可降為止,再結合其他條件,建立含參數的方程或不等式,就可求出參數的值或者取值范圍。
三、證無根:通過討論函數的單調性,證明方程f′(x)=0 無根
有些函數的一階導數f′(x)是無零點的,即f′(x)=0 無解,當利用導函數求函數f(x)在區間[a,b],[a,b)或(a,b]上的最值時,可首先考慮函數f(x)在該區間上是否具有單調性,若具有單調性,則f(x)在區間的端點處取得最值(此時若求f′(x)=0的根,則此方程是無解的).
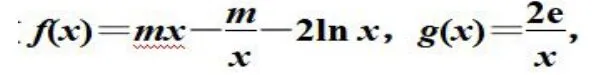
例題3.已知m∈R,函數若Ex0∈[1,e],使得f(x0)>g(x0)成立,求實數m 的取值范圍
分析:因為當x=1 時,f(x)=0,g(x)=2e,不存在f(x0)>g(x0),所以關于x 的不等式f(x)>g(x)在[1,e]上有解,即關于x的不等式
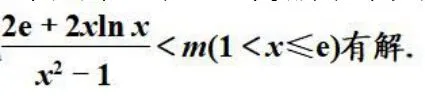
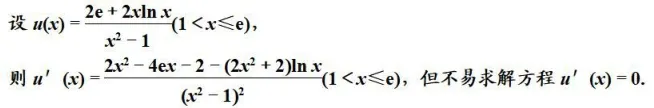
可大膽猜測方程u′(x)=0 無解,證明如下:
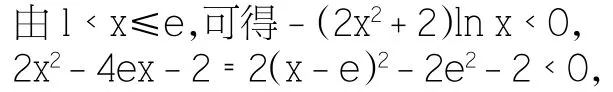
所以u′(x)<0,u(x)在(1,e]上是減函數,

求函數零點問題,是高考試卷中的熱點問題,這類問題常以基本初等函數或分段函數為載體,考查函數零點的存在區間、確定零點的個數、參數的取值范圍、方程的根或函數圖象的交點等問題。不僅考查考生計算、畫圖等方面的能力,還考查考生函數與方程、數形結合及轉化化歸等數學思想的綜合應用。在解決函數零點問題時,除了應用上面介紹的三種辦法外,既要注意利用函數的圖象,也要注意根據函數的零點存在性定理、函數的性質等進行相關的計算,把數與形緊密結合起來。所以學生在平時的訓練中要有意識的加以培養和應用。

