農村初中生數學學習能力提升初探

【摘要】本文結合作者長期農村初中數學教育實踐，根據農村學生數學能力成長的特點，提煉初中數學課程能力增長的核心點，關注數學學科的核心素養養成，激發學生學習數學的興趣，將復雜的數學知識變得簡單易學，體驗數學的數學的圖形美、思維美，變被動學習為主動求知。

【關鍵詞】初中數學課程能力增長的核心點;初三學生的數學能力薄弱點;數學學習能力

農村學生學習數學的特點：花時間少、練習少，按照波利亞的觀點，貨源充足和組織良好的知識倉庫的尚未完全構建，但是農村初中學生數學核心素養有成長快，有興趣就能堅持的特點。

一、提高數學運算能力和對概念的抽象運用能力，構建貨源充足的知識倉庫

講授新湘教版反比例函數時候，大部分學生掌握的較好，講授初三第二章一元二次方程時候，很多學生對配方法求解一元二次方程的解不理解，弄不明。究其原因對平方和平方根的概念理解不透徹。應對策略：

1：找準初中階段數學運算能力的核心運算能力點平方與開平方，平方運算是因式分解和分式化簡、二次根式運算的基礎。開方運算和概念的理解是進行一元二次方程求解、二次函數學習的基礎。

2：停止新授一元二次方程求解，對1到20內整數進行平方，得到平方數，以頭腦風暴的形式檢測記憶效果，學習興趣濃厚。對開平方的概念進行梳理，以搶答賽形式檢測開方運算能力。

二、鼓勵學生大膽觀察猜想得結論，歸納聯想得解法，構建思維嚴謹組織良好的知識倉庫

教師可以通過引導，啟發學生自己建構基本模型，有了自主建構的活動經驗，學生才能有效地將模型內化為己有，在解題時適時構造，靈活應用。

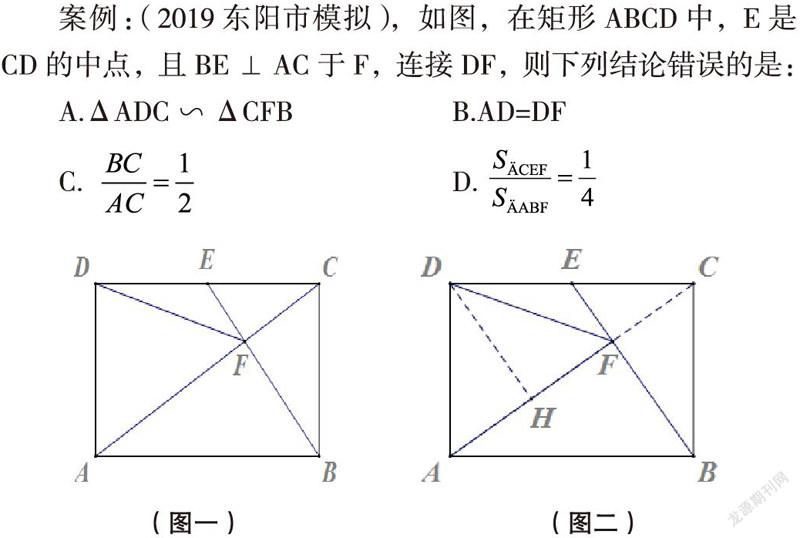
案例：（2019東陽市模擬），如圖，在矩形ABCD中，E是CD的中點，且BE⊥AC于F，連接DF，則下列結論錯誤的是：

圖一易得：結論A和D正確，若C成立，則∠CAB=300該結論不能驗證。B也正確，如何驗證AD=DF，常規想法是證明兩線段所在三角形全等或∠DAF=∠DFA，觀察和推理良久，無法解決。返回題中E是CD的中點進行聯想，而且易得AF=2CF，易聯想中垂線和中位線，連接D和AF中點H，問題得解。

三、借助幾何畫板，讓知識的倉庫構建更加生動形象嚴謹

幾何畫板不單是作圖的根據，更是體驗對稱美、動態美、數形結合思想的秘籍寶典。

案例2：如圖：臺風中心位于點O處，并沿東北方向以40km/h的速度勻速移動，在距離臺風中心50km的區域內受到臺風影響，在點正東方向km的地方有一城市A

（1）A市是否受到臺風的影響？為什么？

（2）在O北偏東150方向，距離80km的地方還有一個城市B，請問B市是否受到臺風的影響？若受到影響，請求出受到影響的時間？若不受影響，請說明理由？

問題設計與幾何畫板設計

1：如何畫點到直線距離，畫板演示

2：模型動圓區域演示如何影響點A和B，得出d和r的關系，若d>r，臺風區域不影響點所在城市，若d≤r，臺風區域影響點所在城市。

3：圓B與動圓圓O半徑相等，圓B與OC交點L和N，，當動點在線段LN上時候，臺風區域影響城市B，連接BL、BN，計算LN的長度，問題得解。

通過幾何畫板的演示和問題的分層設計，學生對該難題有了深刻的領悟，數形結合的思想和能力在動畫得以生成。知識倉庫的升級和拓展有生動形象化的平臺，學生感知數學知識的對稱美、動態美、思維美，極大豐富的聯想能力，興趣得到拓展。

參考文獻：

1.[美]波利亞，著.數學的發現：對解題的理解、研究和講授[M].劉景麟，曹之江，鄒清蓮，譯.北京：科學出版社，2006.

2.吳丹丹.初中生解題能力培養的若干策略[J].中學數學，2018（6）.

湖南省漣源市石馬山鎮湖泉中學?羅六初