高中數(shù)學習題課的選題策略研究

芮雪妮

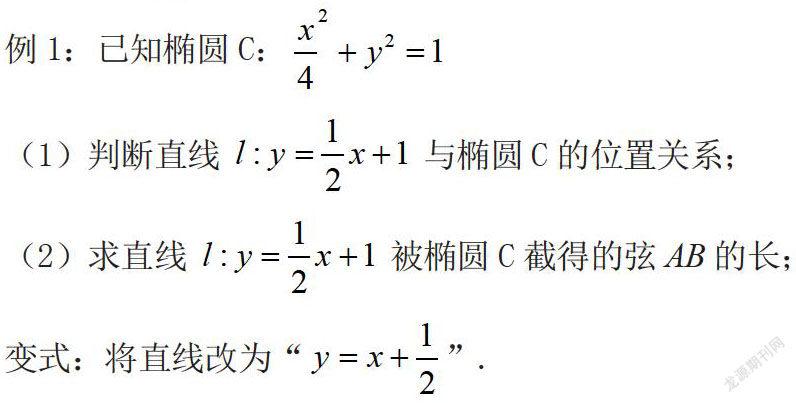
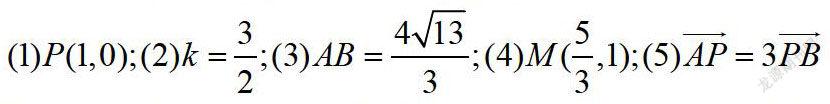
摘 要：習題課，被定義為“學生在教師面對面的指導下，對指定題目進行解題作業(yè)的一種教學形式”。這種教學形式在數(shù)學教學中尤為重要。它能夠幫助學生更好地了解我們學習的知識點應(yīng)該怎么用，用在哪兒，從而總結(jié)經(jīng)驗，提高解題效率。要上好一節(jié)習題課要做到課前精心準備，課堂精彩講授，課后跟蹤反饋。而本文將結(jié)合本人教學經(jīng)歷與見聞，著重談一談習題課課前準備過程中的選題策略，希望對廣大數(shù)學教師有所幫助。

關(guān)鍵詞：數(shù)學習題課;主題明確;典型性;遞進原則;鞏固性原則

數(shù)學教學中，教師常常會花一整節(jié)課去研究習題，這些習題旨在訓練學生學會運用所學知識，從而幫助學生更加深層次的理解新知，并達到能利用知識解決一類問題的程度，像這樣的課通常稱為習題課。

習題課在數(shù)學教學中是非常有必要的。數(shù)學是一門基礎(chǔ)學科，它作為工具，是一切科學的基礎(chǔ)，所以我們要會用數(shù)學知識解決問題。而當下，許多學生都有這樣的一個困境，聽知識點一聽就會，但做題一做就懵，自己也說不明白是哪里不懂，很難從題目中提取到關(guān)鍵信息，也無法迅速將已有的認知和問題準確聯(lián)系起來，導致做題常常會走偏，甚至都無從下筆，這種現(xiàn)象在高中特別常見。而要解決這樣的問題，就需要教師通過習題教學使學生形成解決一類問題的方式方法，或者說是掌握解決一類問題的“套路”，從而培養(yǎng)學生應(yīng)用知識去分析問題、解決問題的能力。

正因為習題課十分必要，所以備課階段“如何選題”“選什么題”就顯得尤為重要。選擇合適的題目，能夠讓學生在充分的練習中掌握方法。那么本文就將以選題問題作為切入點，結(jié)合筆者課堂教學經(jīng)驗，探討習題課備課階段選題的幾項原則。

一、整節(jié)課主題要明確

數(shù)學教學中有這樣一類老師，他們很辛苦，面對茫茫題海，他們無法抉擇，生怕學生會錯過任何一道題。一節(jié)習題課，他們可能會拿出四五道，甚至更多道“好題”，這些題目包含的方法多種多樣，都很精彩。但解決完后呢？不能說所有學生都毫無所得，但對于相當一部分同學，尤其是基礎(chǔ)稍薄弱，解題能力本就欠缺的同學來說，他們一節(jié)課也就會做這幾道題了，換一個情境，該不會的還是不會。

我認為一節(jié)習題課要有一個主線：這節(jié)課你想讓學生學什么？是想讓學生掌握一類問題的解法;又或是讓學生在訓練中規(guī)范書寫;再或是讓學生在習題教學中感受數(shù)學思想，如以算代證思想、數(shù)形結(jié)合思想……而選題自然也要符合主線，不能走題，東一榔頭西一棒，讓學生摸不著頭腦。既然是課，就要有所得，新授課得的是知識，習題課得的是方法。

二、切入題選擇要具有典型性

確定好主題后，就要根據(jù)主題選擇適當?shù)睦}，所謂適當，就是要典型，尤其是切入題，也就是首道例題。

在我們選擇切入題時，教師應(yīng)避免以下問題出現(xiàn)：

（1）題目綜合性太強。希望一道題能包含多種思想，既能體現(xiàn)本節(jié)課主題，又能包含其他知識。自認為選題很完美，能讓孩子學到很多，殊不知沖淡了主題。教師很可能需花大量時間在復(fù)習舊知上，但對于基礎(chǔ)薄弱的孩子來說，短暫的復(fù)習并沒有什么用。并且對于你想讓他掌握的方法他也無心去學了。

（2）計算量過大。運算量大無疑就是難度加大，學生在大量運算中，關(guān)注點會發(fā)生偏離，忘了題目本身想讓我們得到的思想方法，這是毫無必要的。尤其作為首道例題，一上來就給學生一個下馬威，下面就很難進行了。

（3）解題過程繞彎太多。題目不難，但過程太繞，同樣也會耗費學生大量精力，不適合課堂講解，也是教師給自己找“麻煩”。

綜上所述，我們所選擇的切入題需要能夠直接反映主題，它可以是一類數(shù)學題的代表，或是體現(xiàn)一類數(shù)學思想的代表。題海無邊，當我們掌握了方法，無疑是乘上了一條能在題海中自由游行的船，讓學生事半功倍，真正學會應(yīng)用知識。同時，切入題的過程、計算都不需要太過復(fù)雜，主要是讓學生掌握方法，而不是為難學生。

下面是本人在“直線與橢圓位置關(guān)系”教學中選擇的切入題，以及選題分析。

本節(jié)課主題是探討直線與橢圓位置關(guān)系，并且學會應(yīng)用代數(shù)法解決位置關(guān)系相關(guān)問題，尤其是相交問題。針對這樣的主題，我設(shè)計了切入題，它包含三個小題。

第（1）小題，旨在教會學生判斷直線橢圓位置關(guān)系的一般方法——聯(lián)立求。

三、例題間須符合遞進原則

一節(jié)習題課不只有一道例題，例題間，筆者認為：應(yīng)遵循遞進原則，層層深入，由淺入深。我們備一節(jié)習題課其實就像寫一篇文章，要有一條邏輯線，符合主題的情況下，題與題之間也需要關(guān)聯(lián)，且層層遞進，能讓學生在掌握上一題的基礎(chǔ)上，自然而然、順理成章地過渡到下一題的解題思路中去。

例如上文提到的“直線與橢圓位置關(guān)系”一課中，我選擇的例2是：

這道題較例1難度有所提升，已知弦長求直線，是一個典型的含參問題。但是方法是類似的，通過聯(lián)立、設(shè)而不求，韋達定理，用參數(shù)表示出弦長，構(gòu)造等式，求出參數(shù)b。通過這樣一個遞進，學生能夠更加深層次的理解弦長公式。同時這樣的含參問題，或者說是待定系數(shù)求直線的方法正是解析幾何常見的求解方程方法，這也與之前學習的內(nèi)容巧妙的結(jié)合起來了。

緊接著告訴學生，其實不只是求弦長，聯(lián)立后利用韋達定理其實是直線與圓錐曲線問題的通法，過渡到下一道例題。

這道題中要求直線方程，可以待定系數(shù)，設(shè)直線斜率，接下來還是固定套路求解。這里完全可以讓學生探討出思路后展示求解過程，充分體現(xiàn)出學生的主觀能動性。完成講解后，再提問：“這道題是否還有其他解法呢？”事實上根據(jù)這道題“中點”條件的特殊性，我們還可以采用點差法求解，充分體現(xiàn)出“一題多解”在數(shù)學題中的應(yīng)用，并進行總結(jié)思考：什么時候可以用點差法呢？培養(yǎng)學生發(fā)散思維。

也就是說所謂遞進原則，是由淺入深，由單一知識到綜合應(yīng)用，由多題一解的深刻性走向一題多解的發(fā)散性的過程。這樣的過程也符合教育心理學的要求，順應(yīng)學生的心理發(fā)展，更利于學生接受。

四、課后反饋題符合鞏固性原則

在課堂上處理習題的時間是有限的，一節(jié)課四十五分鐘，能將思想方法總結(jié)到位已實屬不易，要想真正掌握，還離不開課后習題的選擇。而課后的反饋題必須符合鞏固性原則。鞏固性原則是教學原則之一，要求學生所學的知識、技能達到牢固和熟練的程度，能夠在需要的時候及時地、準確地再現(xiàn)出來。課后反饋題就是讓我們鞏固，從而真正掌握的一個過程，所以題目要能很好地反映這節(jié)課的重點，而不是一堆題型大鍋燉。

曾有幸聽過一節(jié)關(guān)于“直線與拋物線”的習題課。

課上例題：已知拋物線y2=3x的焦點為F，過點P作直線l交拋物線于A、B兩點，線段AB中點為M，

課上老師將（1）（2）作為條件，可以推出（3）（4）（5），并讓同學思考了：可否選擇（2）（3），推出（1）（4）（5）？最后得出結(jié)論，實際上只要知道任兩個條件都可以推出其他結(jié)論。課后反饋題目是讓學生嘗試選擇不同的選項作為已知條件，自己編題證明。充分的發(fā)揮了學生的主觀能動性。

這節(jié)課給了我很多啟發(fā)，學生課后練習如果僅僅是機械性的重復(fù)，甚至是大量重復(fù)，就很難做到靈活變通。而課上時間有限，課下同學之間交流探討的時間是很長的，不妨在可行的情況下，通過這樣開放性的題目讓學生鞏固的同時，積極思考，合作交流，相信對學生掌握方法會很有價值。最后反饋練習中教師可以根據(jù)學生層次差異設(shè)置一兩道“選做題”。尊重學生之間的個體差異，拓展學生的視野，增強學生的學習興趣。

習題課的教學值得探討和深思的還有很多很多，本文也僅能通過短短篇幅簡略地表達我的一些思考。真正在教學中，要想讓學生一節(jié)習題課上的有價值，不僅僅要重視選題，選完題如何針對不同層次學生去講？如何將學生講明白？……還需要更多的實踐總結(jié)。總之，我們數(shù)學教師要在充分理解數(shù)學課程標準的基礎(chǔ)上，將培養(yǎng)學生核心素養(yǎng)作為出發(fā)點，研究每一堂課，包括習題課。要知道，在實際數(shù)學教學過程中，習題課所占比重是非常大的。要努力克服傳統(tǒng)習題課的弊端，要使勞動有價值。“題海無邊，回頭是岸”，我們要多思考，多研究，提高教學質(zhì)量。

參考文獻

[1]韋宏，張桂玉，黃美玲.數(shù)學習題課教學的弊端與創(chuàng)新[J].智庫時代，2019，No.201（33）：221-222.

[2]劉梨鳳.初中數(shù)學習題課變式教學的幾點建議[J].新智慧，2019，（04）：108.

[3]王登，喬世紅.習題課教學策略及注意事項[J].新課程（下），2019，No.471（01）：126.

[4]李銀耀.新課改條件下如何上好數(shù)學習題課[J].考試周刊，2010，（30）：14-15.

[5]任云崗.數(shù)學習題課教學的有效性探析[J].讀與寫（教育教學刊），2010，v.7（01）：172.

[6]張景中，張奠宙.數(shù)學習題教學研究[M].上海：教育出版社.2010