船舶工業與國民經濟的耦合協調度評價與預測研究

羅清?夏慧玲?吳晶晶

摘要：本文以2007-2018年我國船舶工業與國民經濟的發展數據為樣本，運用耦合協調度模型對兩者的耦合度及耦合協調度進行分析與研究，結果表明兩者耦合協調度總體上呈現螺旋上升的變化規律、由中度失調向勉強協調的發展水平演化。同時根據2007-2018年耦合協調度的計算結果，運用非平穩時間序列預測模型ARIMA（p，d，q）對耦合協調度的變化趨勢進行預測，預測結果表明，到2022年兩者的耦合協調水平發展到初級協調階段，兩者的協調發展水平有所上升。

關鍵詞：耦合協調度;ARIMA模型;船舶工業

一、引言

船舶工業是我國的一項戰略性產業，主要為海洋開發、運輸以及國防裝備等提供載體支持，屬于技術、資本以及勞動密集型的總裝制造業。在世界航運市場需求低迷、我國造船產能嚴重過剩、船企盈利困難等經濟形勢下，我國船舶工業圍繞產業政策，不斷加大產業深度融合的力度，推動產業結構轉型升級。在船舶工業“十三五”發展規劃的指導方針下，研究其與國民經濟的耦合協調發展規律及未來發展趨勢，對船舶工業產業結構有序優化和轉型升級具有一定的實踐價值。

二、耦合協調度模型及評價指標體系構建

（一）指標體系構建與數據來源

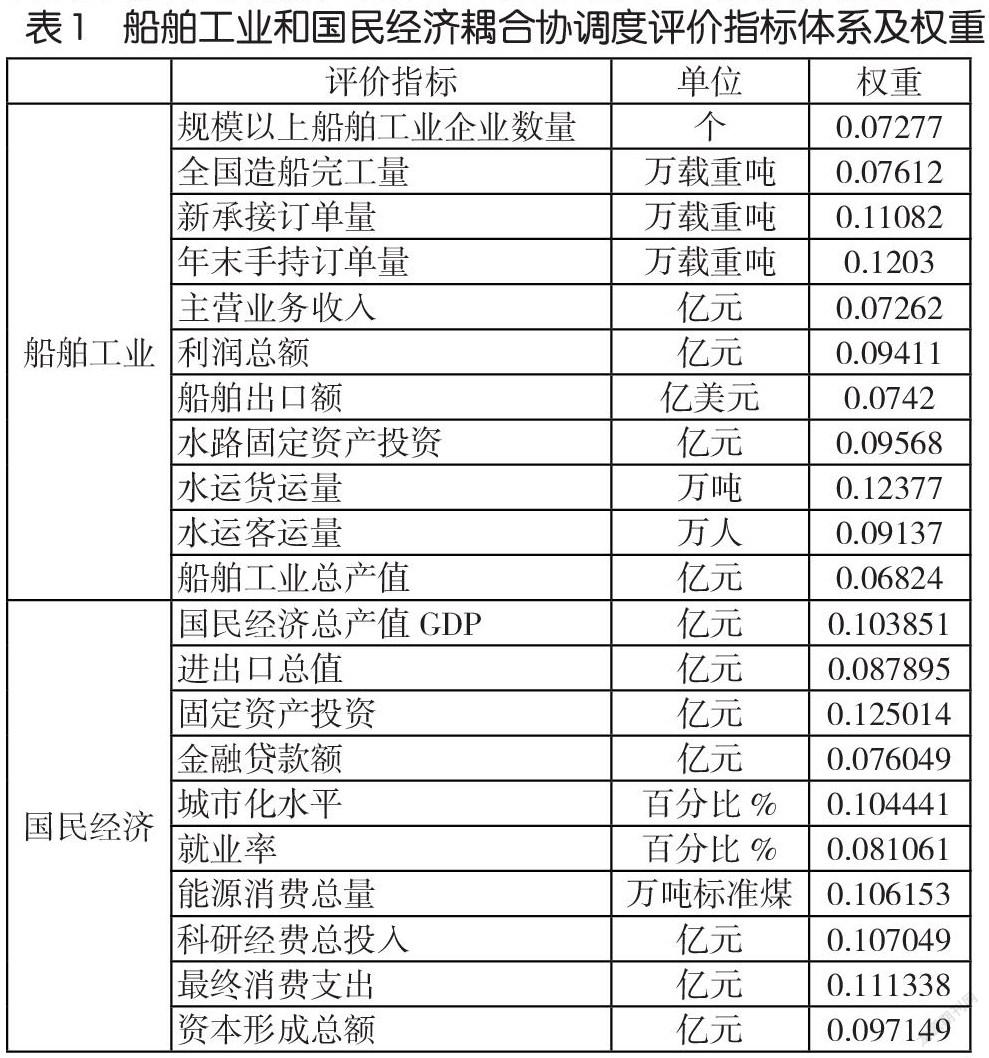
對船舶工業與國民經濟的耦合協調度進行評價的前提就是要構建一個科學合理的評價指標體系，所選取的指標具有可獲得性及代表性。本文在參考相關文獻資料的基礎上，結合實際，選取了船舶工業和國民經濟的21個指標，具體見表1。

本文船舶工業和國民經濟數據的采集區間為2007-2018年，數據主要來源于中國統計年鑒、中國船舶工業統計年鑒、船舶工業經濟運行分析報告、交通運輸網、交通運輸行業發展統計公報、中國科技統計公報等，對于部分缺失數據采用回歸估計等方法補齊。

（二）評價指標權重的確定

本文采用熵權法來確定指標權重，步驟如下：

1.對各指標運用極差變化法進行標準化處理，從而消除量綱帶來的誤差。

2.運用熵權法計算第j項指標的熵值ej：

，其中，。

3.算第j項指標的熵權wj：

（三）耦合協調度模型的構建

1.計算各產業的綜合評價指數

本文以船舶工業和國民經濟的綜合評價指數為基礎，其計算公式為：。式中，i=1，2;u1，u2分別表示船舶工業和國民經濟的綜合評價指數;yij為第i個產業系統的第j個指標的標準化值，即功效系數;wij為第i個產業系統的第j個指標的權重值。

2.計算耦合度

耦合度用來反映不同系統之間相互作用和相互影響的程度。其計算公式為：

式中，C為耦合度，其取值區間為[0，1]，C值越大，說明不同系統之間的有序程度越高;反之則有序程度越低。

3.計算耦合協調度

耦合協調度的值反映了不同系統之間的協調程度，其計算公式為：;。式中，D為耦合協調度;T為船舶工業和國民經濟的綜合評價指數;α，β分別為船舶工業和國民經濟綜合評價指數的待定系數，由于船舶工業與國民經濟對兩業融合程度的貢獻度相當，α，β的取值均為0.5。D值越大，說明不同系統之間的耦合協調性越好。耦合協調度的評價標準如表2所示。

三、船舶工業與國民經濟耦合協調度分析

根據船舶工業與國民經濟各指標的功效系數及指標權重，對2007-2018年兩者的耦合度及耦合協調度進行計算，計算結果如表3所示。

根據表3的評價結果分析如下：

（一）自2007年以來，國民經濟的綜合評價指數由0.0903292增長到0.8947832，其綜合發展水平處于不斷上升的趨勢;船舶工業的綜合評價指數由0.144612增長到0.606183，總體呈現出上升趨勢，發展也較為穩定，但是與國民經濟的發展速度相比，船舶工業的發展速度還是較為緩慢，還有較大的提升空間。另外，從船舶工業與國民經濟的綜合評價指數對比來看，2007-2012年船舶工業綜合發展水平高于國民經濟綜合發展水平，國民經濟處于發展的滯后階段，說明該時期船舶工業帶動了國民經濟的發展，船舶工業對兩者的耦合協調發展的貢獻較大;2013-2018年國民經濟綜合發展水平高于船舶工業，出現了船舶工業發展滯后的現象，說明該階段由于船舶工業的滯后發展導致兩者的耦合協調發展水平受到制約。從整個研究階段來看，兩者協調發展關系存在一方處于滯后型，沒有出現同步型的情形，導致兩者未能達到高度協調發展的水平。

（二）船舶工業與國民經濟的耦合度C總體較為穩定，總體在0.5左右，表明兩者之間屬于中度耦合程度，處于耦合發展的初期階段，還需要不斷優化船舶工業產業結構，增強其與國民經濟的耦合程度。

（三）從耦合協調度來看，除了2016年和2018年有所下降外，船舶工業與國民經濟之間的耦合協調度總體上呈現螺旋上升的態勢，耦合協調情況由中度失調水平達到了勉強協調的水平，說明兩者的相互作用越發明顯，但仍處于較低水平的協調階段，兩者的耦合協調達到有序協調發展還需要一定的時間。

四、船舶工業和國民經濟耦合協調度的預測

（一）ARIMA（p，d，q）模型

ARIMA（p，d，q）模型實質就是差分運算與ARMA模型的組合，對于非平穩序列yt經過d次差分后變為平穩序列，則yt是d階單整序列。令，wt為平穩序列，然后對wt建立ARMA（p，q）模型：。式中，p為自回歸模型的階數，q為移動平均模型的階數，d為差分次數。

（二）ARIMA（p，d，q）模型在耦合協調度預測中的應用

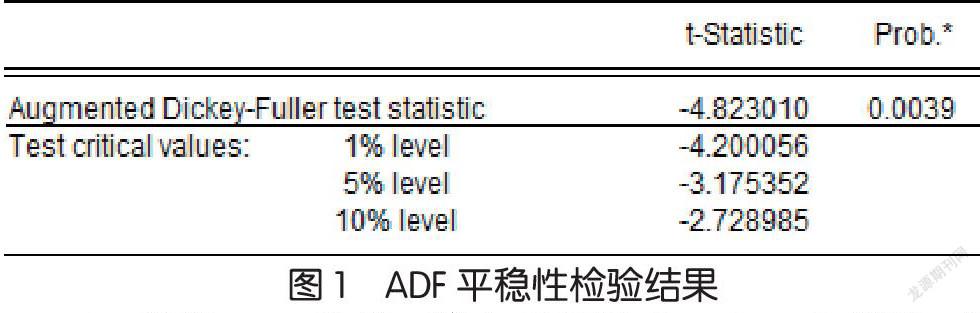
1.序列平穩性檢驗。利用ADF單位根檢驗方法對2007-2018年我國船舶工業與國民經濟的耦合協調度進行序列平穩性檢驗，結果如圖1所示。t統計量的值為-4.82301，小于給定檢驗水平的臨界值，所以拒絕“包含單位根”的原假設，原序列視為平穩序列，差分次數d=0。

2.確定p、q的值，建立ARIMA（p，0，q）模型。對上述平穩序列進行自相關和偏自相關分析，由PACF和ACF初步確定p為1，q為1。然后根據貝葉斯信息準則BIC，最終確定Dt模型為ARIMA（1，0，0）。

3.參數估計與檢驗。利用spss對ARIMA（1，0，0）模型進行時間序列預測，從結果可以看出，R的平方達到0.898，擬合程度較好，AR的系數為0.842，顯著性水平小于0.01。預測模型為：Dt=0.842Dt-1+et。

估計的模型是否合適還需要判斷其殘差序列是否滿足白噪聲序列，如果殘差序列是白噪聲序列，那么模型是合適的，如果不是白噪聲序列，就需要對模型進行調整。運用自相關圖對模型的殘差序列進行檢驗可知，殘差序列的ACF和PACF值均處于5%的置信區間內，不存在相關性，所以模型的殘差序列屬于白噪聲序列，可用上述模型來預測。ARIMA（1，0，0）模型對我國船舶工業和國民經濟耦合協調度預測的結果如表4所示。

從表4可看出2019-2022年兩者耦合協調度始終處于上升趨勢，預測的兩者耦合協調度的平均值為0.626175，相比2018年的耦合協調度的值來說增長了13.7%，預測到2022年兩者的耦合協調發展水平上升為初級協調階段，兩者的耦合協調度有所增長，主要原因是 “十三五”期間《船舶工業深化結構調整加快轉型升級行動計劃（2016-2020年）》的有效實施以及船舶產業結構調整。

五、結論

本文運用耦合協調度模型和ARIMA模型對我國船舶工業與國民經濟耦合協調度的發展規律進行分析和預測。研究結果表明：兩者耦合協調度總體上呈現螺旋上升的變化規律、由中度失調向勉強協調的發展水平演化;從兩者的綜合發展水平對比來看，船舶工業與國民經濟的發展沒有出現同步型，兩者的發展水平不均衡，在一定程度上制約了兩者的耦合協調發展;從兩者耦合協調度的預測來看，我國船舶工業與國民經濟耦合協調度呈現出上升的趨勢，耦合協調水平上升到初級協調階段。

船舶工業與國民經濟的發展水平不均衡，制約了兩者耦合協調發展水平。針對上述問題，建議營造良好的金融服務環境，建立風險投資和融資保障機制，拓寬融資渠道、創新金融模式，幫助船企緩解資金壓力，解決中小船企融資難的問題;提升船舶工業的科技創新水平，優化船舶工業的產業鏈結構，明確其產業定位以及制定有效的船企淘汰機制。

參考文獻：

[1]陳治國，陳儉，杜金華.我國物流業與國民經濟的耦合協調發展[J].中國流通經濟，2020，（1）：9-20.

[2]徐小峰，劉家國，郝俊.船舶工業與經濟系統融合程度分析—以青島市為例[J].哈爾濱工程大學學報，2017，（1）：140-146.

[3]李曉萍，王淑芹，周清.船舶工業與物流業耦合協調度評價及預測研究[J].數學的實踐與認識，2020，（6）：19-26.

[4]孫敬水.計量經濟學（第4版）[M].北京：清華大學出版社，2018.

[5]李根，張光明，劉家國.我國船舶工業技術效率地區差異及收斂性分析[J].中國造船，2017，（58）：170-182.

科研項目：江蘇省高校哲學社會科學研究基金項目（2018SJA1283）;南通市熱點課題（RL1945）。

作者簡介：

羅清（1986—），女，湖北荊州人，講師，碩士研究生，研究方向：產業經濟。