串級控制系統的PID參數自動整定算法分析
高瑞


摘要:在本文的分析過程中,主要針對控制系統的動態響應過程進行分析,以FFT變換為重要的手段,對串級系統的輸入以及輸出的實際增幅,進行詳細的分析,以此能夠得出主、副對象的頻域特性,之后再利用降階的方式,得出二階模型,進而對主副回路的PID參數進行自動整定算法以及公式的確定。
關鍵詞:串級控制;PID;自動整定;二階模型
引言:對于串級控制系統以及單回路控制系統而言,就兩者的控制原理進行比較分析,其重要的區別在于,串級系統可以獲得可測中間變量,同時可以充分的利用這一變量,構成負反饋的閉環控制回路,其中擾動對中間變量的干擾作用,會對控制系統產生一定的影響,這就需要預先進行調節,從而改善整個控制系統的動態品質達到良好的控制效果。
一、串級系統與單回路系統
在串級控制系統當中,主副回路當中比較容易產生共振,以此會對控制器,或者是PID控制器的參數整定,產生了較大的困難。一種比較經典的參數整定方法,就是需要基于經驗進行參數值試湊,但是在實際進行的過程中,往往無法確定可以得到較為理想的控制效果。在本文的分析過程中,主要針對本質穩定的動態響應過程,利用FFT算法變換到頻域當中進行分析,對其控制系統的主副回路,所表現出來的對象特征,進行準確的辨別,從而得出控制系統的降階模型。在分析的過程中,便可以依據串級系統當中的實際特點,以及實際的需求,確定出PID參數自動整定的公式。
二、模型頻域特性的辨識
(一) 單回路閉環系統的辨識
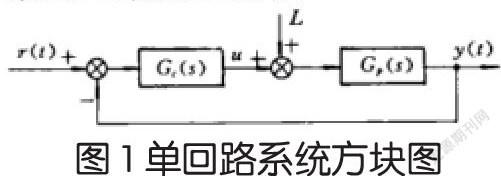
如上圖1所示,是單回路系統的方塊圖。我們需要輸入r(t),輸出y(t),之后便可以對其閉環頻域辨識進行分析,以此可以有效的獲得對象模型Gp(s)的具體頻域特征,在其設計控制器Gc(s)的過程中,需要對系統進行有效的控制。
而對于單閉環控制器而言,其中Gs(s)往往是一種純比例控制,因此其增益可以設定為Kt。在對其擾動進行分析的過程令L=0,這樣就可以在輸入中,得出閉環頻域的實際特性。
在動態分析的過程中,通過對輸入以及輸出的結果分析來看,其控制器的增益Kc,在增加的時候,能夠有效的對其負載干擾K產生抑制的效果,同時在Kc的增加過程中,需要盡可能的控制在一定的范圍當中,從而避免對整個系統的穩定性產生明顯的影響。
(二)串級回路控制系統的辨識
基于上述的分析方法,可以有效的得出對串級系統的辨識方法,同時在其控制回路中,同樣可以將控制器設計為純比例的控制,同時增益可以有效的進行區分,假定擾動值都為零,這樣就可以在給定輸入r(t)當中,得到相應的y(t)值,以此能夠對其外環閉環的頻域特性進行分析。
同時在其內環開環頻域特征的分析過程中,可以進行各種公式的推導,在帶入到設計定出來的公式之后,可以將其內環對象的頻域特性參數確定下來,讓其設計出來的內環控制器,可以符合相應的合理參數值。在這樣的基礎之上,可以對外環對象進行進一步充分的修正。通過這樣的分析方法,可以求得相應的臨界頻率,并確定出臨界增益。在分析的過程中,一般情況下串級回路當中的內環響應會比較快,基于這樣的原理在數據上也可以進行二次的驗證。同時,其外環頻域的實際特性也能夠有所保障,在控制算法的計算過程中,可以有效設計出外環控制器當中的參數。
三、系統降階模型的獲取
對于已知的頻域特性分析的過程中,需要在對其控制器設計的過程中,進行系統的動態響應特性的分析以及研究,明確出開環時間的常數值、時滯,以及對其進行大小的比較分析。因此,在參數自整定的過程中,通過一個近似降階模型的建立,能夠基于工程項目在實際應用過程中,具體作用的層面分析。在本文的分析過程中,其選擇二階加上純滯后模型的建立,進行分析過程比較具有合理性和準確性。
在進行辨識的過程中,其系統的閉環動態品質方面,主要的影響因素就是在G(jwi)當中的實際相角。通過引入激勵信號的頻域響應分析,使得可以在相應的數據源中,獲得準確的結果的數據K,并有著較高的效率。同時在串級控制中,一般情況下主回路通常選擇PI或PID控制器,副回路通常選擇P或PI調節器。在保障了控制系統負反饋通道單位增益的同時,使串級控制系統獲得更好的動態性能。
四、PID控制器設計
基于串級系統的實際特征,在對副對象進行選取的過程中,一般情況下副回路需要盡量包括所有的純滯后因素,以及能夠具備著較快的動態響應。而對于主對象而言,主回路里面要避免又包含著較大的時滯。在對串級控制系統進行參數整定的要求,就是為了避免主副回路在工作的過程中,特別是在較高的工作頻率下,既能夠保證穩定性又能夠動態響應,避免產生共振現象。這就需要在副回路當中,采用PI控制的方式,同時還需要適當的增加積分時間,以此能夠保障副回路,成為一個單調響應的環節。通過這樣的操作,就可以有效地提升副回路在控制過程中的控制效果。特別是在小時滯的動態響應過程中,能夠影響到整個控制系統的響應特性,對于抗擾能力的提升有很好的作用。一些著名的學者,也提出了優化抗干擾能力的其他方式,但是其方式在對給定值,進行跟蹤的過程中,表現效果并不理想。
因此在本文的設計過程中,就采用了一種“混合式”的方式,在綜合主、副對象的頻域特性之后,需要首先依據上文所述,進行降階建模,以此能夠有效的得到副對象的降階模型,之后再依據本文討論的分析方式,可以有效的獲得無時滯的具體指標參數。
同時,在得到副回路的控制器的時候,也就直接獲得了副回路的閉環等效特性。在得到了主回路當中的開環特效的特性之后,可以充分的利用降階的方式,得到相應的模型,因此在這個自整定過程當中,基本上都保證了控制系統的動態穩定,同時以最快的速度能夠確定出PID/PI參數自整定公式。
五、仿真結果
在分析的過程中,需要針對本文設計出來的方法,通過仿真試驗的方式,對整定算法的可靠性進行驗算。
其中副對象的取值確定下來后,還需要對主對象進行明確,之后將其初始比例控制器,設定為2和1,在完成相應的整定之后,其系統會在t=1的以及t=50的時候,加入2或者-2的給定值階躍,并在t=100的時候,其L2位置,需要計入20的階躍擾動,而在相對的位置上,加入-20的階躍擾動。
在對其方法效果進行充分的比較之后,基本上可以采用兩種不同的方法進行整定,并且其方法都能夠有效的應用于主副回路當中,以此會得到相應的控制器參數值。其中在具體的分析過程中,可以通過下圖2所示:
在圖2當中,其可以進行相應的動態響應分析,可以發現,在曲線的位置2處,其抗干擾性以及跟蹤特性,都有著良好的表現;其控制品質方面,明顯大于曲線的實際效果。因此在本文提出的自整定方法在實際的應用過程中,具有良好的控制效果。
總結:綜上所述,在對串級控制系統的PID參數自動整定算法分析過程中,由于其系統的復雜程度,需要針對各種問題進行優化以及調整,從而得出相應的具有較高跟蹤特性以及抗干擾能力的整定方式,并對其進行了仿真的實驗研究,得出具有良好的效果。
參考文獻:
[1]陳思. 基于數據的生產裝置PID應用研究[D].北京化工大學,2018.
[2]王健. 繼電反饋PID控制器參數自整定及其應用[D].東北電力大學,2016.
[3]鄺濤. 上灣換熱站節能控制系統設計與研究[D].西安建筑科技大學,2016.

