Lamb波與缺陷相互作用的散射特性研究
王勃
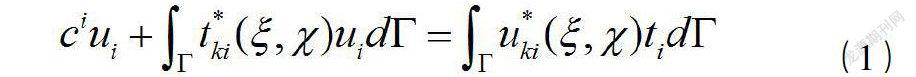

摘要:結構健康監測和無損檢測目的是缺陷的識別和定位分析。對于超聲導波缺陷檢測,關鍵是要探討導波與缺陷之間相互作用時的散射特性。利用邊界元和模態擴展相結合的方法(BEM-NEMT),本文探討Lamb波與不同類型缺陷間相互作用的散射特性。在此基礎上,詳細討論了分析模型缺陷的尺寸和銳度、不同激發頻率和入射模態、缺陷的幾何對稱性等對Lamb波散射特性的影響,分析結果可為各零部件(如內燃機)缺陷的識別、檢測模態和頻率的選取提供依據,降低研制周期和成本,從而提高產品性能、功能得到一定的價值效果。
關鍵詞:Lamb波;缺陷;散射;無損檢測
0? 引言
在超聲無損檢測中,缺陷回波的原始信號和周圍的噪聲摻雜在一起,被噪聲所污染,有用的缺陷信號不能很好的被辨別出來,所以在檢測中信號處理十分重要[1]。不同類型和尺寸的缺陷所產生的回波信號不同,其對結構安全性的影響也是不同的,有的缺陷對結構的安全性有非常大的影響,甚至造成結構的失效(如裂紋),有的則幾乎不影響結構的正常運行[2]。所以,缺陷的識別和定位分析是信號處理中不可或缺的一部分。我們所熟知的Lamb波,是板結構超聲無損檢測中一種常用的超聲導波。在對板結構進行健康檢測和無損檢測時,討論Lamb波與不同缺陷類型的相互作用具有十分重要的意義。本文利用BEM-NEMT法對Lamb波與幾種不同的缺陷類型相互作用的散射特性進行了探討,以期為板結構無損檢測中缺陷的識別、模態和頻率的選擇等提供技術支持。
1? 理論分析
本文所采用的研究方法是邊界元與模態擴展技術相結合的方法,簡稱BEM-NEMT方法。該方法采用邊界元程序,與模態擴展技術所得到的邊界條件相結合,對問題進行聯合求解。本文從含有缺陷的無限長板中,取出帶缺陷部分的局部區域作為研究模型,我們知道波動問題在傅里葉變換域中的邊界積分方程為:
2? 程序實現
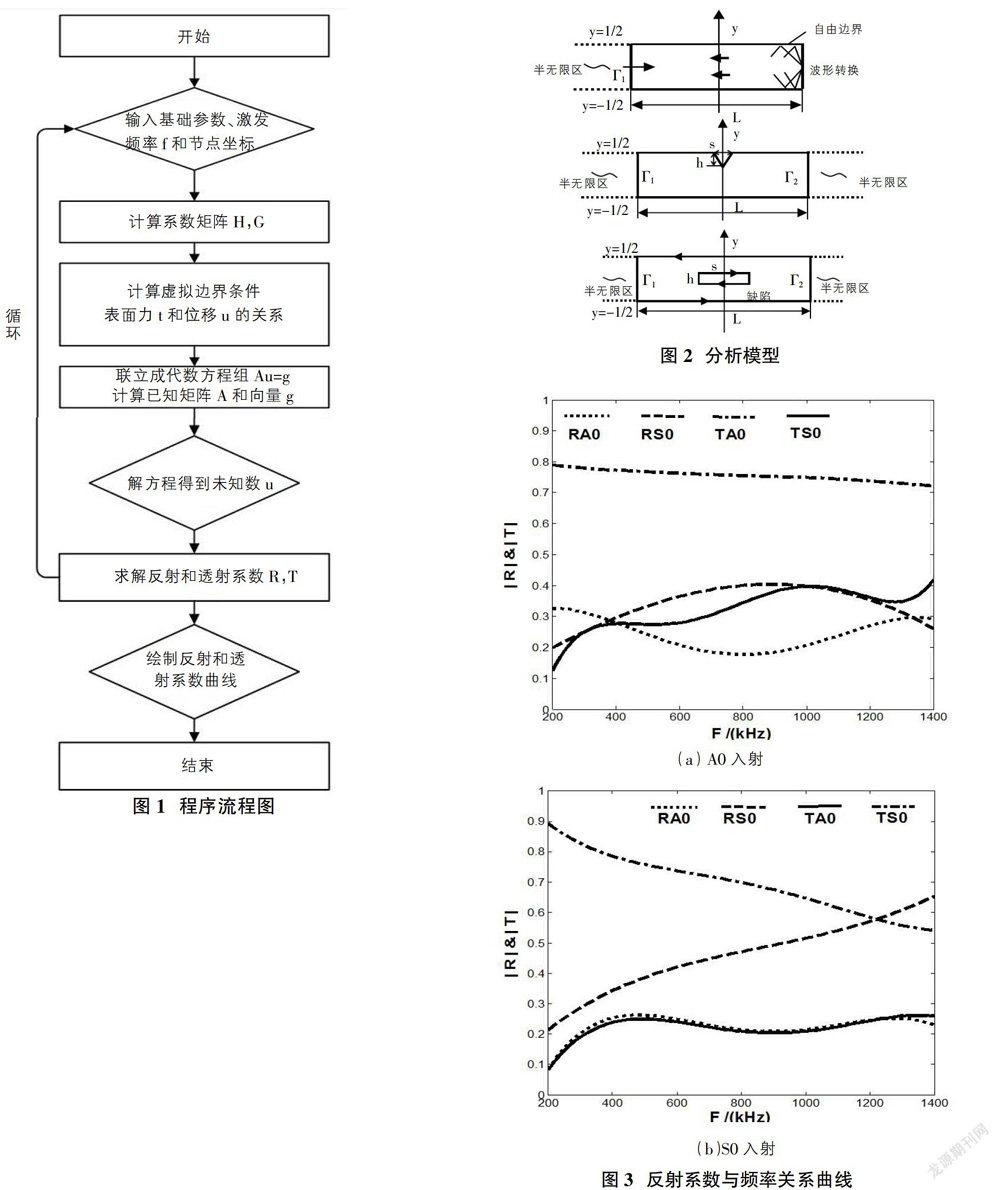
由于求解方程比較復雜,本文編寫程序協助求解,實現程序結構分為三部分:一是所需參數的輸入;二是系數矩陣的計算和方程的求解;三是導波散射圖的繪制。具體的運行過程見圖1。
3? 數值結果分析
數值模型采用1mm厚的鋼板,其中蘭姆常數為118.8Gpa,橫波波速3200m/s縱波波數5490m/s,分析模型件圖2,反射系數和頻率關系曲線示意見圖3。
3.1 自由端邊界
分別用反對稱模態A0和對稱模態S0作為入射波,來探討Lamb波與自由端的相互作用。
在第一截止頻率之前,RA0基本保持在1.0左右,RS0為零,這說明入射模態A0沒有發生任何的波形轉換。而當頻率超過第一截止頻率時,A0模態發生了波形轉換,部分能量轉換為A1模態,RA0先迅速減小,而此時RA1最大。之后RA0逐漸增大,RA1逐漸減小,而RS0始終為零。值得注意的是RA0和RA1隨頻率的變化趨勢是相反的,這滿足能量守恒原理。在自由邊界處的入射模態S0沒有發生任何的波形轉換,S0模態為波導中的主導傳播模態。
3.2 表面三角形缺陷
入射模態A0的反射RA0和透射TA0隨頻率的變化不是很明顯,RA0隨頻率先增加后減小,TA0隨頻率逐漸減小,減小幅度很小,變化幅度不是很大。并入射模態A0發生了波形轉換,部分能量轉化為S0模態。入射模態S0模態的反射RS0和透射TS0隨頻率的增加分別單調遞增和單調遞減。這與A0模態入射時所表現的趨勢不同,隨頻率的變化幅度很大,這說明對于三角形缺陷S0模態比A0模態更敏感。
3.3 內部缺陷
入射模態A0發生了波形轉換,轉化幅度不大,A0模態的反射和透射變化趨勢相反,一個單調增加,一個單調遞減。而轉換模態S0的反射和透射隨頻率的變化不是很明顯,基本隨頻率的變化呈遞增趨勢,增加幅度很小。入射模態S0的散射隨頻率變化不很明顯,透射TS0的變化區域平穩,反射RS0的變化稍有起伏但幅度很小,同時轉化模態A0的散射隨頻率的變化也很微小。這說明A0模態可以用來辨別邊界缺陷和內部缺陷,而S0模態則不適合。
4? 結論
綜上所述,經過對導波與不同種缺陷類型的散射特性的理論基礎和數值分析,可以得出以下結論:
①表面邊界和自由邊界關于中性軸的非對稱性,會引起對稱模態和反對稱模態之間的轉換;而入射模態一旦超過它的截止頻率,就會轉換為其他模態,如自由邊界模型中A0轉換為A1模態,并且入射波的反射隨頻率減小,達到與最小值,之后再次增加;②反對稱A0模態比對稱S0模態更適合用來辨別邊界缺陷和內部缺陷;③反射和透射的變化主要依賴于缺陷的銳度和入射波的選擇,而次生的轉化模態主要受缺陷銳度的影響,此結論與文獻[5]得出的結論一致。
參考文獻:
[1]張廣明,馬宏偉,等.超聲無損檢測中的缺陷識別與噪聲抑制[J].中國機械工程,1999,10(12):1389-1391.
[2]何輔云.石油管道的高速檢測與缺陷識別[J].無損檢測, 2000,20(5):206-211.
[3]王珅,黃松嶺,趙偉.平板蘭姆波與缺陷作用邊界元仿真實現研究[J].中國機械工程,2009,20(8):887-891.
[4]楊德全,趙忠生著.邊界元法理論及應用[M].北京:北京理工大學出版社,2006,12.
[5]Rose J L. Ultrasonic waves in solid media, Cambridge University Press, 1999.
[6]Rose J L, Zhang W, Cho Y. Boundary element modeling for guided wave reflection and transmission factor analyses in defect classification. IEEE Ultrasonic Symposium, 1998, 1: 885-888.

