齒輪傳動系統的動態性能分析和優化設計

李文善

摘要：為了分析多級齒輪傳動系統的動態性能，構建了齒輪傳動系統仿真模型，通過仿真，分析多級齒輪傳動系統的主要物理參數對于齒輪傳動系統動態性能的影響規律。并基于仿真得到的分析數據據和相應的實驗測試數據，提出了應用諧波平衡法的多級齒輪傳動系統優化設計方法，并獲得最優設計參數。

Abstract： In order to analyze the dynamic performance of the multi-stage gear transmission system， a simulation model of the gear transmission system is constructed. Through the simulation， the influence law of the main physical parameters of the multi-stage gear transmission system on the dynamic performance of the gear transmission system is analyzed. And based on the analysis data obtained by simulation and the corresponding experimental test data， a multi-stage gear transmission system optimization method based on the harmonic balance method is proposed. The housing size parameters of the reducer and the basic parameters of the gear pair are used as design variables. The transmission ratio， actual center distance， gear tooth strength， etc. are constraints， and the root mean square value of vibration acceleration and the overall mass are the goals. A multi-objective hybrid discrete optimization model is established， and the program is solved based on the branch and bound algorithm to obtain the optimal design variable.

關鍵詞：齒輪傳動系統;動態性能;優化設計

Key words： gear transmission system;dynamic performance;optimization design

0? 引言

多級齒輪傳動系統相較于普通齒輪傳動系統而言，具有體積小、質量輕、傳動效率高、傳動精度高、承載能力高等眾多優勢。精密設備的控制系統對于多級齒輪的傳動性能在靈敏度界限、工作快速性和穩定性方面提出更高的要求。因此，有必要對多級齒輪傳動系統的動態性能開展相關的研究。

1? 建立多級齒輪傳動系統的動態性能分析模型

1.1 構建多級齒輪傳動系統的數學模型

依據剛度特性，多級齒輪傳動與一般齒輪傳動之間具有一定的差異，并且在負載與執行件之間安裝徑向嚙合式多級齒輪傳動的主要目的是為了傳遞動力、實現運動，所以必須要考慮到彈性與齒間側隙的影響[1]。通過綜合考慮彈性與齒間側隙的影響，構建數學模型。

而模型中的IL為負載慣量，IM是執行電機轉子和波發生器的慣量，制定電機的轉角？漬M（t）進行折算，使其到輸出軸上的轉角以？漬M（t）=？漬M（t）/ih。

當系統存在齒間側隙為2jt的情況下，可以采用以下的方程式來表示方程組。

從上述的公式中，充分考慮了元件彈性以及齒間側隙的影響，其是一個非線性函數。在多級齒輪傳動系統中，將電機到負載的系統當量為兩個具有彈性元件的鏈接，為間隙隔開集中質量的運動傳遞，模型中的Ii為IM折算到輸出軸上的慣量，？漬i（t）與Ti則為折算到輸出端的輸入轉矩和轉角。

1.2 建立多級齒輪傳動系統動態性能仿真模型

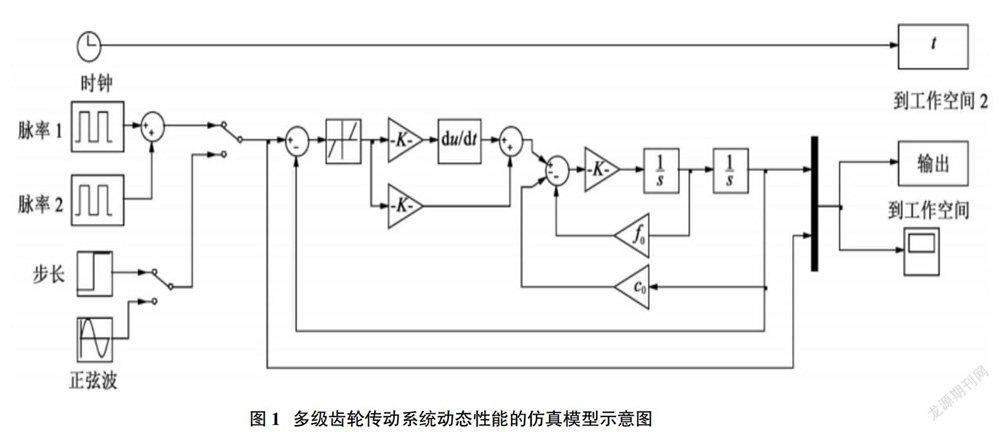
在對于多級齒輪傳動系統的動態性能建立數學模型后，利用SIMULINK組件能夠實現多級齒輪傳動系統的動態性能仿真模型的構建[2]。如圖1所示為仿真模型。

1.3 仿真分析和結論

對于多級齒輪傳動系統動態性能建立仿真模型，后進行仿真分析，從而確定傳動系統中的主要物理參數，得出對于整個系統性能產生的影響規律。

利用某研究項目中應用的多級齒輪減速器為仿真對象，總傳動比i=80、柔輪變形波數U=2，鋼輪齒數z2=162，柔輪齒數z1=160，輸入軸轉速fH=9500r/min，嚙合角？琢n=20°，額定負載60N·m，輸入端轉動慣量J1=0.00022kga·m2，輸出端轉動慣量J0=0.2839kg·m2，0是初始條件。通過進行各種試驗之后，能夠得出扭轉剛度表達式各項，而齒間側隙則是2？漬i=8′。

在設定仿真參數之后，將上述的各項參數開展仿真分析，以此來得到這些參數對于傳動系統性能所產生的影響規律。

2? 傳動系統非線性振動特性的分析

對微分方程組進行求解，求解所用積分時間范圍為300Tm。求解時，需要對二階振動微分方程逐步進行降階處理，方程可表示為：x2=f（t，x（1），x（2））。

2.1 轉速對于系統非線性振動特性的影響

齒輪傳動正逐步向高速和重載的方向發展，因此有必要對轉速影響系統振動特性開展系統的研究，設定傳動系統的無量綱頻率在？贅=0.001～1.5在范圍內變化。當？贅<0.2時，系統呈現出單周期的非諧響應特性。此時，系統位移反映的時間歷程圖即單周期曲線，并且頻譜圖分布在m？贅的離散點上。隨著無量綱頻率的增加，系統將會由倍周期分叉進入混沌運動。隨頻率的逐漸加大，系統響應狀態呈無規律的反復變化，且運動的狀態也更為復雜而多變，混沌區域出現了眾多的周期性窗口，同時窗口寬窄呈現交替漸變趨勢。隨著頻率的再次升高，齒輪副動載荷系數也將隨之加大，系統將在無沖擊狀態下顯現單邊及雙邊沖擊。當無量綱頻率增至1附近時，動載荷系數出現最大值，沖擊情況最為嚴重。

2.2 黏滯摩擦因數對于傳動系統性能的影響

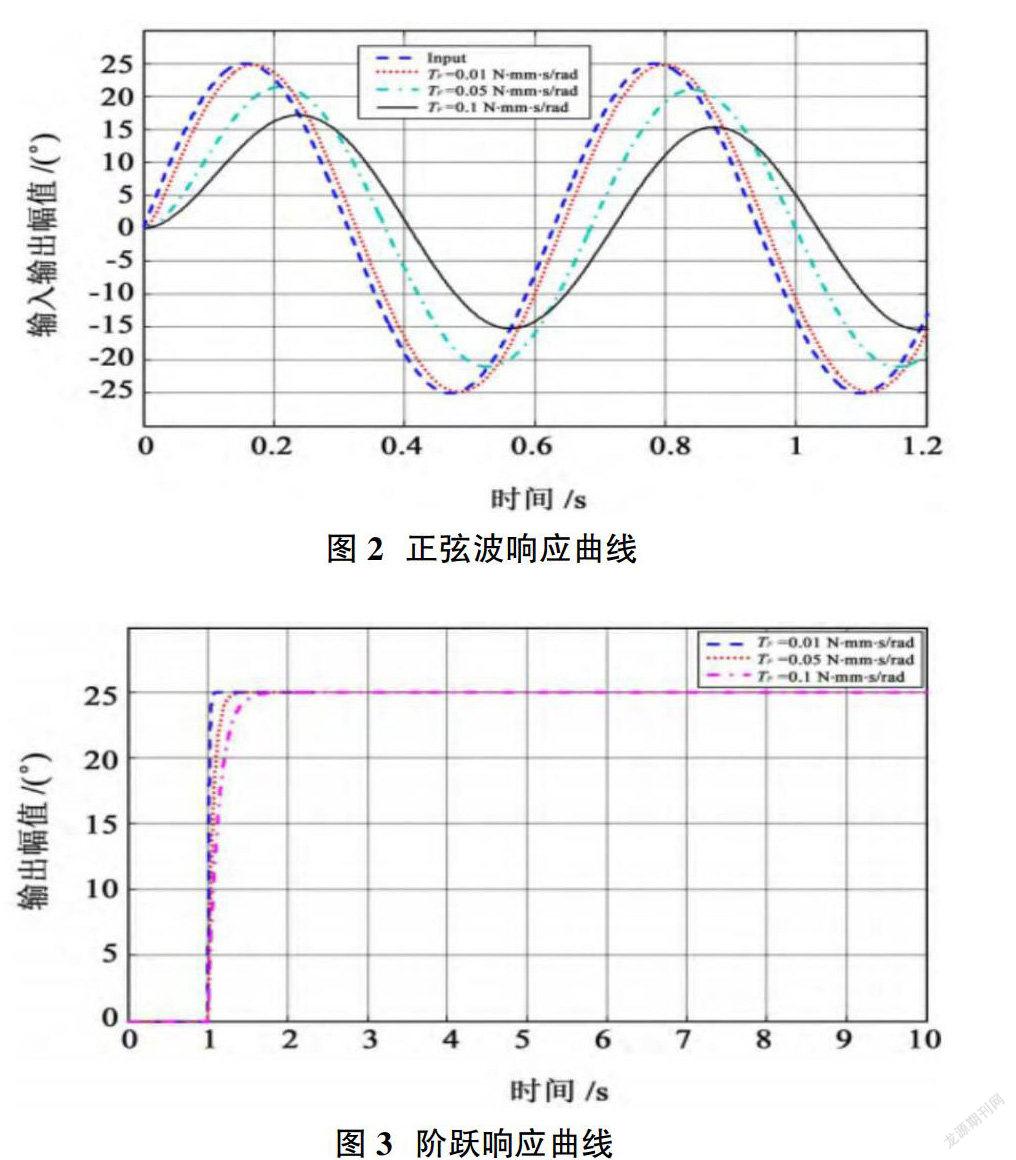
利用仿真分析可以得知在不同黏滯摩擦因數的響應曲線，如圖2所示，而系統階躍響應曲線如圖3所示。

通過圖2、圖3，能夠得到傳動系統中黏滯摩擦因數對于傳動系統的動態性能所造成的影響。隨著黏滯摩擦因素的不斷增加，而傳動系統的相位差也在逐漸的擴大，出現這一問題的主要原因在于：隨著黏滯摩擦因數的上升，傳動系統中的摩擦力矩也會隨之上升，這表示隨著摩擦動態方程中阻尼項參數的不斷上升，將會出現這些反應[3]。除此之外，還會導致多級齒輪傳動系統中，機械效率逐漸出現下降情況。因此，在設計傳動系統的過程中，必須要考慮傳動系統的一定速遞效率、一定快速性，在這一前提條件下，可以有效的降低系統的粘滯摩擦因數。

2.3 齒間側隙對于多級齒輪傳動系統的性能影響

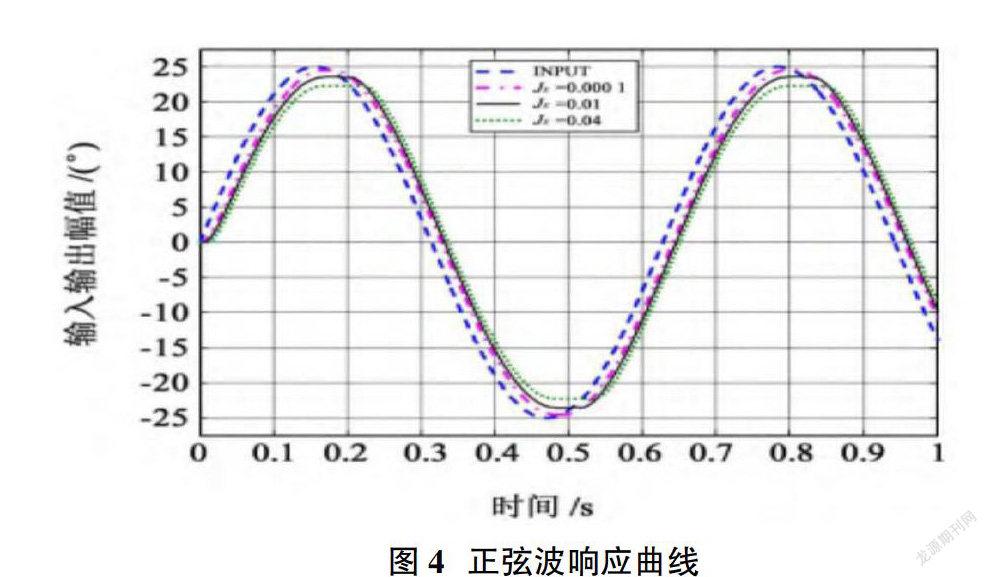
如果構建仿真模型采用齒間側隙的話，其響應曲線如圖4所示。而在采用不同齒間側隙后，如圖4所示為系統的階躍響應曲線。

基于圖4的曲線圖，傳動系統的傳動間隙對于系統動態性能的影響主要體現在：當傳動系統存在間隙時，響應的穩定性和快速性都會下降，同時因為存在間隙，所以雖然傳動系統可以達到最佳的穩定狀態，但是傳動系統也同樣會存在一定振幅的振動，并對于整個工作的穩定性造成嚴重的影響[4]。所以，在對于多級齒輪的傳動系統進行設計和制造等過程中，需要以系統運動潤滑為前提，同時滿足這一前提條件下，盡可能的消除傳動系統中所存在的裝配間隙與其誤差，以此來保障傳動系統的設計功能。

3? 多級傳動系統的優化設計

3.1 優化設計變量

多級齒輪減速器具有結構復雜的特性，充分考慮減速器的安裝環境及條件，設減速器外型尺寸不出現較大變化，隨后逐一選取傳動系統和對應殼體中的關鍵性幾何參數作為設計的變量。傳動系統的設計變量為齒輪的模數（m）、齒數（Z）和齒寬（b），對應殼體的變量分別為各子塊的壁厚（β），累計設置15個變量，其變量矩陣表達式：

3.2 目標函數

綜合考慮減速器的抗振性及輕量化設計等兩個方面的具體要求， 同時密切注意到傳動系統與殼體間的振動響應幅值處存在較大差別的實際，采用線性加權組合法，構建出目標函數：

3.3 約束條件

一般而言，多級齒輪的總傳動均比較大，考慮到齒數優化后可能會引起減速器總傳動比發生變化，所以需要對總傳動比提前進行約束。此外，因多級齒輪傳動系統中存在最小齒數與總傳動比之間合理分配的實際情況，且各齒輪齒數應取整數，故對應的取值范圍如下：

眾所周知，齒輪的大齒寬對應高強度。但齒寬過大會導致齒輪載荷分布不均勻，因此有必要設置寬徑比約束條件。實際生產中，為便于加工和測量，通常將齒寬的結尾數值取0和5。綜上所述，齒輪寬徑比約束取值范圍如下：

3.4 優化模型求解

多級齒輪傳動系統動態性能優化模型其實質為一個多目標混合離散規劃，離散設計變量為齒輪的m，整型設計變量分別為z、b和β。本文利用Matlab軟件和分枝定界法思想編程求解，其算法的基本過程簡述如下：

首先，確定相互嚙合的各級齒輪m的組合，其可行域設定為6。

其次，獲得滿足齒數、裝配、傳動比、鄰接和中心距等約束條件的齒數組合可行閾值。

第三，在確定的齒輪m和齒數等約束條件下，逐步求解滿足輪齒強度、寬徑比約束條件的齒寬可行域6;隨后，獲取目標函數的局部最優解并存儲相關信息。

最后，變換m及z再次進行計算，便可獲得局部最優解集合，局部最優解集合中使目標函數最小的設計變量即為全局最優解[5]。通過上述混合離散優化求解，便可得到多級齒輪傳動系統的設計變量最優值。忽略齒側間隙和摩擦力矩等非線性因素會在一定程度上影響到優化計算的準確性，為檢驗優化效果，將優化后設計變量值，代入考慮非線性因素的減速器耦合系統集中參數模型中，計算構件的振動加速度和質量，將優化后各構件的振動加速度均方根值和質量除以優化前的相應值，可得到優化后振動加速度均方根值和質量的相對值[6]。

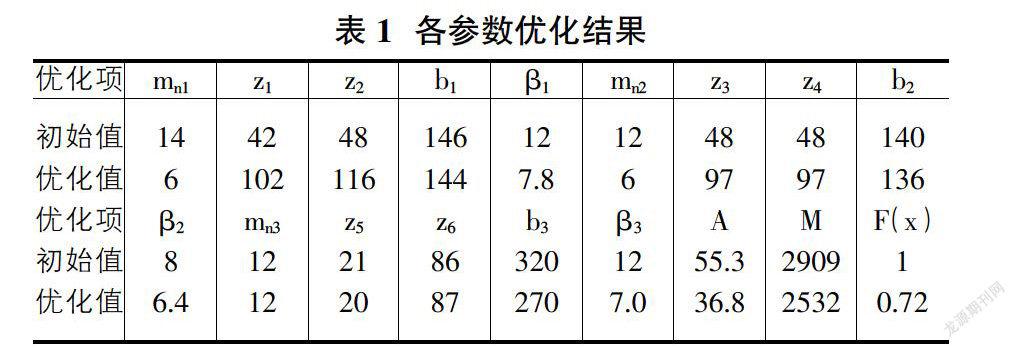
3.5 優化結果

優化后的具體結果如表1所示。優化后多級齒輪傳動系統中的振動速度降低，傳動系統構件振動加速度均方根值平均降低36.8m/s2，較優化前減小了33.5%，實現了減振的目的;傳動系統質量降為2532kg，較優化前減小了12.96%。

4? 結語

綜上所述，通過分析齒間側隙對多級齒輪傳動系統的動態性能造成的影響，以此為基礎構建傳動系統的模型，通過仿真，分析傳動系統中的齒間側隙、黏滯摩擦因數等主要參數對系統動態性能的影響。最后，通過對某一型號的多級齒輪傳動系統進行優化，得到了優化參數，并且傳動系統重量減輕，性能也得到了提高。

參考文獻：

[1]張強，李洪武.車輛多級行星傳動系統扭振特性分析與優化[J].機械科學與技術，2019，38（3）：339-343.

[2]孫剛，任尊松，辛欣，等.高速動車組齒輪傳動系統振動特性[J].機械工程學報，2019，55（18）：104-111.

[3]吳濤，周建星，張文祥，等.行星齒輪傳動系統動態均載性能與靈敏度分析[J].機械設計與制造，2019（4）：171-175.

[4]鄭凱峰，李偉，程立勇，等.模擬發動機驅動的變速器傳動系統動態性能臺架試驗[J].汽車零部件，2019（6）：68-70.

[5]崔慧娟.齒輪傳動系統動態特性與傳動效率研究[J].內燃機與配件，2019（15）：73-74.

[6]符升平，項昌樂，姚壽文，等.基于剛柔耦合動力學的齒輪傳動系統動態特性[J].吉林大學學報（工學版），2011，41（2）：382-386.