一種改進的寬帶自適應波束形成器

安瑞雪， 王曉林， 陳舒文， 張 偉

(1.電子科技大學信息與通信工程學院， 四川成都 611731； 2.北京控制與電子技術研究所， 北京 100038；3.中國航空工業集團公司雷華電子技術研究所， 江蘇無錫 214063)

0 引言

作為陣列信號處理的研究難點與熱點，寬帶波束形成已廣泛應用在雷達、無線通信、聲吶和地質勘探等眾多領域中。目前寬帶波束形成最為流行的處理方法是空頻處理和空時處理[1]。

空頻方法是將寬帶信號在頻域劃分子帶，對每一個窄子帶進行窄帶波束形成后，再合為寬帶信號[2]。此方法的優點是結構簡單，但是需要在劃分窄子帶之前以及窄帶頻域處理后分別進行傅里葉變換(DFT)和反變換(IDFT)，缺點是需要同時處理數據塊，不具有實時性。廣義旁瓣對消(GSC)波束形成器和Frost空時波束形成器是空時處理常見的兩種結構[3-4]，兩者均可實現線性約束濾波，在波束形成與盲多用戶檢測中應用廣泛。Frost[3]提出的線性約束最小方差(LCMV)自適應波束形成設計約束條件使期望信號無損失通過的同時，最大限度地抑制干擾與噪聲。Compton[5]指出干擾抑制后的輸出信干噪比(SINR)與抽頭數和陣元數有關，空時維度越大則干擾抑制后輸出SINR越大。

隨著對抗干擾性能的要求增加，空時維度增加導致計算復雜度增大，難以保證信號實時性處理。稀疏布陣[6]與稀疏表示[7]問題得到廣泛關注，從陣列中抽掉天線單元以降低其成本與計算量。但是寬帶陣列信號稀疏問題并非線性，求解需要借助遺傳算法，費時的同時不一定能求解出期望的最優解[8]。Compton的研究結果[9]表明，時域抽頭數目一致時，SINR可達最大。基于該研究，在Frost結構基礎上稍作改動構建一種高效的可行結構，抽頭數減半，陣列個數保持不變，以降低空時維度，陣列分成奇、偶通道，奇、偶通道后的抽頭延遲數目保持相同，根據通道的奇偶來選取奇偶延遲時間間隔。這種結構降低維度的同時能維持其抗干擾能力，即用較小的代價大大減輕了運算量的負擔。

1 空時自適應干擾抑制結構

窄帶信號情況下，純空域濾波即可實現自適應波束形成。對于寬帶信號，為滿足權值和頻率之間的關系，Frost[3]提出了空時自適應結構，如圖1所示，在M個陣元后均接有N個抽頭，Frost空時結構輸出表達式為

(1)

圖1 Frost空時自適應波束形成結構

權值矢量w為MN維，定義為

(2)

式中，wk為第k階抽頭時延權值，wk=[w0kw1k…w(M-1)k]T，維度為N。

陣元接收信號為MN維，定義為

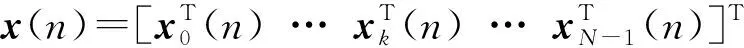
(3)

式中，xk(n)=[x0(n-k)x1(n-k)…xM-1(n-k)]T,k=0,1,…,N-1。

表達式(1)可寫為

y(n)=wHx(n)

(4)

假設期望信號來自均勻線陣的正側面，亦即入射角θ0=0。當此條件不滿足時可通過機械旋轉陣列或者數字時延等方式，將均勻線陣的法線方向對準期望信號，常見的實現方式是整數時延加分數階時延濾波器(FDF)[10]。Frost結構最優化問題可描述為

(5)

式中，Rxx為MN×MN的信號相關矩陣，C為MN×N的線性約束矩陣[3]。當對準期望信號時，約束矩陣C則由向量1和0構成,約束向量f為N維的列向量：

f=[1,0,…,0]T

(6)

優化問題式(5)的最優自適應權值表達式為

(7)

2 改進的寬帶自適應波束形成器

2.1 改進寬帶自適應波束形成器結構

改進寬帶自適應波束形成架構如圖2所示，改進結構在常規Frost結構基礎上抽頭數減掉一半。改進結構共有M個陣元(M為偶數)，陣元的標號標為0,1,…,M-1；并按奇偶標號分為奇偶通道；偶通道陣元標號為0,2,…,M-2，奇通道陣元標號為1,3,…,M-1。橫向FIR濾波器抽頭數為常規Frost結構的抽頭數的一半，即共有(N+1)/2個(N為奇數)。偶通道抽頭延時為偶數倍時間間隔，分別為2T,4T，…,(N-1)T；奇通道的抽頭延時為奇數倍時間間隔，分別為T,3T，…,(N-2)T。

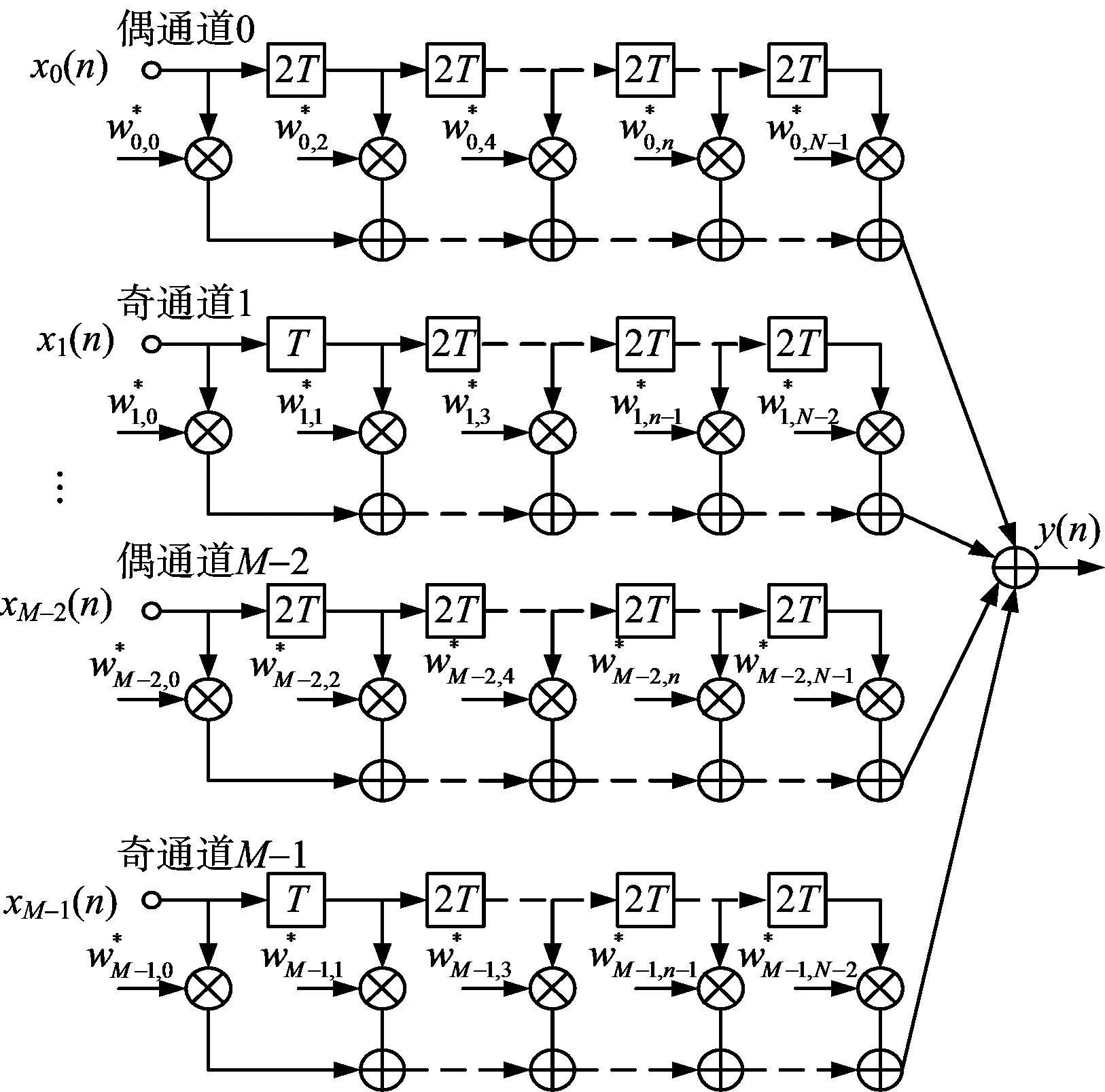
圖2 改進空時波束形成結構

改進結構的變量用符號“-”以標示區分。所以改進結構自適應處理最終輸出為

(8)

且m與k奇偶性一致。

改進結構優化問題描述如下：

(9)

(10)

式(9)的最優解即改進結構的最優自適應權為

(11)

2.2 兩種結構運算量對比分析

根據兩種結構的最優權向量的表達式，式(7)和式(11)可以具體分析矩陣運算過程中的運算量；表1顯示了Frost結構與改進結構分別所需的抽頭個數、權值個數以及自相關矩陣維度、約束矩陣維度以及求逆的次數。

表1 Frost結構與改進結構的運算量比較

由此可以看出，改進結構矩陣乘法運算與求逆運算的運算量明顯低于常規Frost結構，故實時性也要優于常規Frost結構。

2.3 兩種結構干擾抑制性能分析

改進結構在Frost結構的基礎上進行了抽頭數目減半能明顯減小運算量并提高實時性，但是抑制干擾的能力是否減弱需要進一步分析。

陣元數為m快拍數為n時陣元接收信號表達式為

xm(n)=sm(n)+pm(n)+vm(n)

(12)

式中：sm(n)為期望信號，其中sm(n)=s(n- 2πf(m-1)dsinθ0/c)，θ0為期望信號的入射角，常規Frost結構一般假定θ0=0，故而sm(n)=s(n)；pm(n)為干擾信號，pm(n)=p(n)ejγm(θp)，θp為干擾角度；vm(n)為噪聲信號。

將式(12)代入式(1)得到的波束形成輸出為

(13)

(14)

第n次快拍期望信號與干擾信號可表示為

s(n)=[s(n)s(n-1) …s(n-k) …s(n-(N-1))]T

p(n)=[p(n)p(n-1) …p(n-k) …p(n-(N-1))]T

(15)

如式(2)方式,重新排列噪聲信號為

v(n)=[v0(n)Tv1(n)T…vN-1(n)T]T

(16)

且

vk(n)=[v0(n-k)v1(n-k) …vM-1(n-k)]T

(17)

陣列波束形成輸出可表示為

y(n)=aHs(n)+bHp(n)+wHv(n)

(18)

輸出信號的功率表達式為

P(θ)=E{|y(n)|2}=

E{y(n)yH(n)}=

aHE{s(n)sH(n)}a+

bHE{p(n)pH(n)}b+

wHE{v(n)vH(n)}w=

aHRssa+bHRppb+wHRvvw

(19)

式中，Rss維度為N×N，Rpp維度為N×N，Rvv維度為MN×MN。

SINR表達式為

(20)

(21)

由此可知改進結構與Frost結構的期望信號功率是一樣的，表達式為

(22)

Rss{1,1}表示Rss矩陣的第一行第一列元素。期望信號能量在單位時間內是恒定不變的，雖然改進結構抽頭數減了一半，但是抽頭數的數目并不會影響期望信號的能量，故改進結構期望信號的輸出功率不變。

考慮權值不影響期望信號的情況下，優化問題理想化只使得干擾加噪聲輸出功率最小。由于干噪比通常比較大，故目標函數變為干擾噪聲輸出功率最小，式(5)的優化問題可轉化為如下約束問題：

(23)

選取寬帶白噪聲作為干擾信號，fs=2B(fs為采樣頻率，B為信號的帶寬)，式(23)可轉化為

(24)

(25)

對約束條件分類，式(25)中約束問題進一步寫為：

當k=0時，

(26)

當1≤k≤N-1時，

(27)

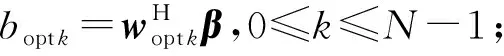
(28)

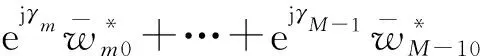
(29)

式(28)為約束條件，式(29)為約束改進結構等于未改進結構的最小干擾值。滿足M>2即有解。

當1≤k≤N-1時，由于改進結構分為奇偶通道，故以k=1(奇數階)和k=2(偶數階)為例，其他階以此類推,k=1和k=2時得到下面的方程組：

(30)

同樣地M≥4時，式(30)表示的方程組才有解。綜合上面方程組分析，當M≥4(M為偶數)且寬帶干擾為噪聲干擾時，兩種結構具有一樣的干擾剩余功率。寬帶干擾為多個且不相關時，可根據式(28)、式(29)和式(30)類推。改進結構需要陣元數為2J來抑制J-1個干擾。

當存在單個寬帶噪聲干擾且M≥4(M為偶數)，改進結構與Frost結構具有相同的期望輸出功率與干擾剩余功率，故兩種結構在理論上的抗干擾能力是一致的，改進結構并沒有因抽頭數減半而導致抗干擾性能下降。

3 兩種結構抗干擾性能對比仿真

仿真實驗共分兩組，兩組實驗的共同仿真條件：

陣列布陣方式為均勻布陣，陣元間距d=λ/2；期望信號：線性調頻信號，θ0=0°，信噪比(SNR)為0 dB，載頻f0=1.2 GHz，帶寬B=400 MHz；干擾信號：寬帶噪聲信號，干擾角度θj=10°，干噪比(INR)為50 dB，帶寬B=400 MHz；噪聲信號：加性高斯白噪聲，功率為0 dB。

仿真實驗一 對比兩種結構抽頭數對抗干擾能力的影響

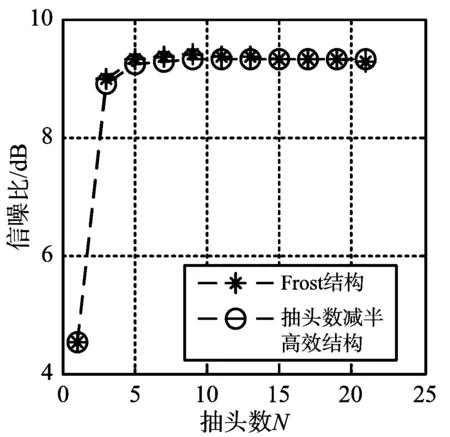
(a) 抽頭數對信噪比影響

(b) 抽頭數對干噪比影響

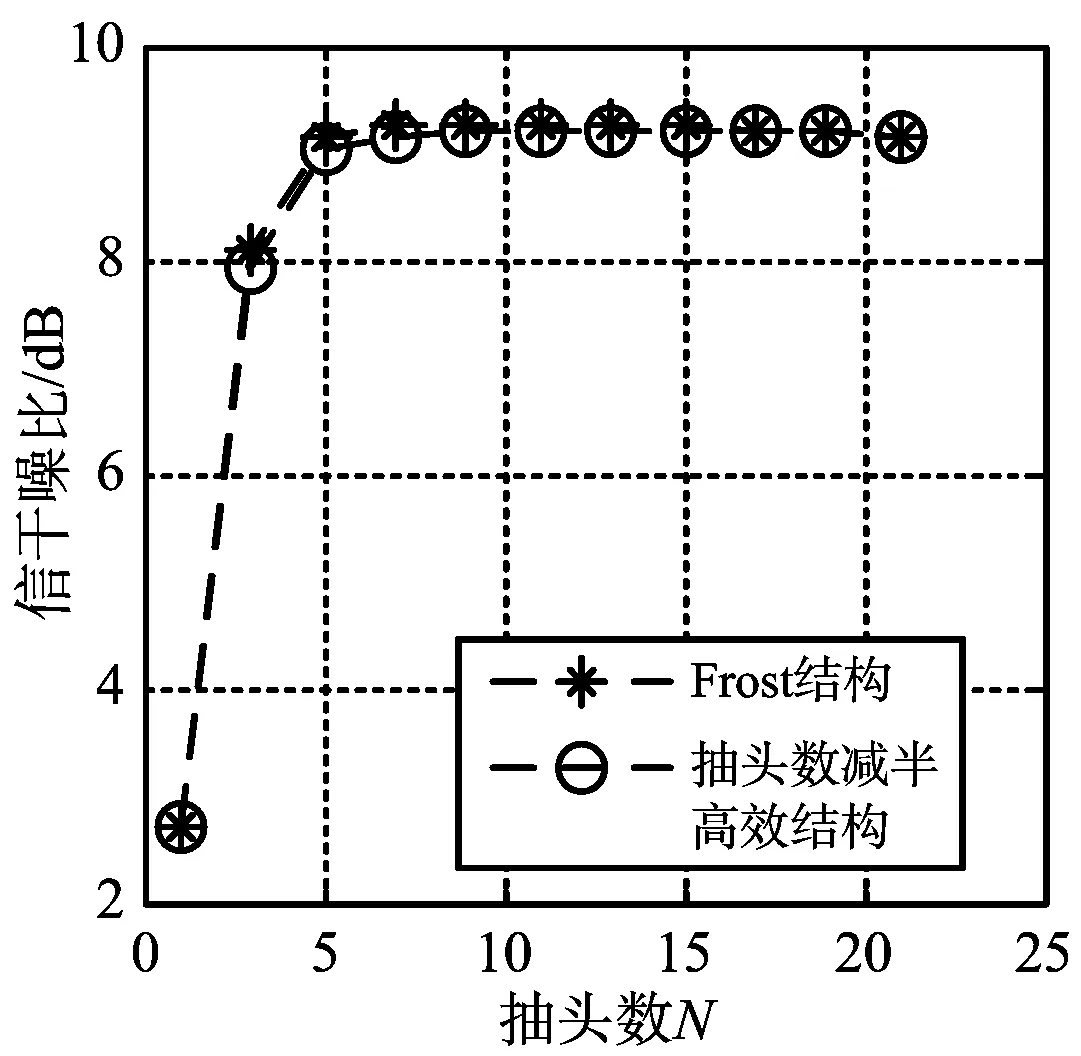
(c) 抽頭數對信干噪比影響圖3 兩種結構抽頭數對抗干擾能力影響對比結果

實驗表明，兩種結構的信噪比(SNR)、干噪比(JNR)與信干噪比(SINR)測試結果均相差不大，這說明抽頭數對兩種結構干擾抑制性能大體相同，結構的不同導致之間存在微小的差別。

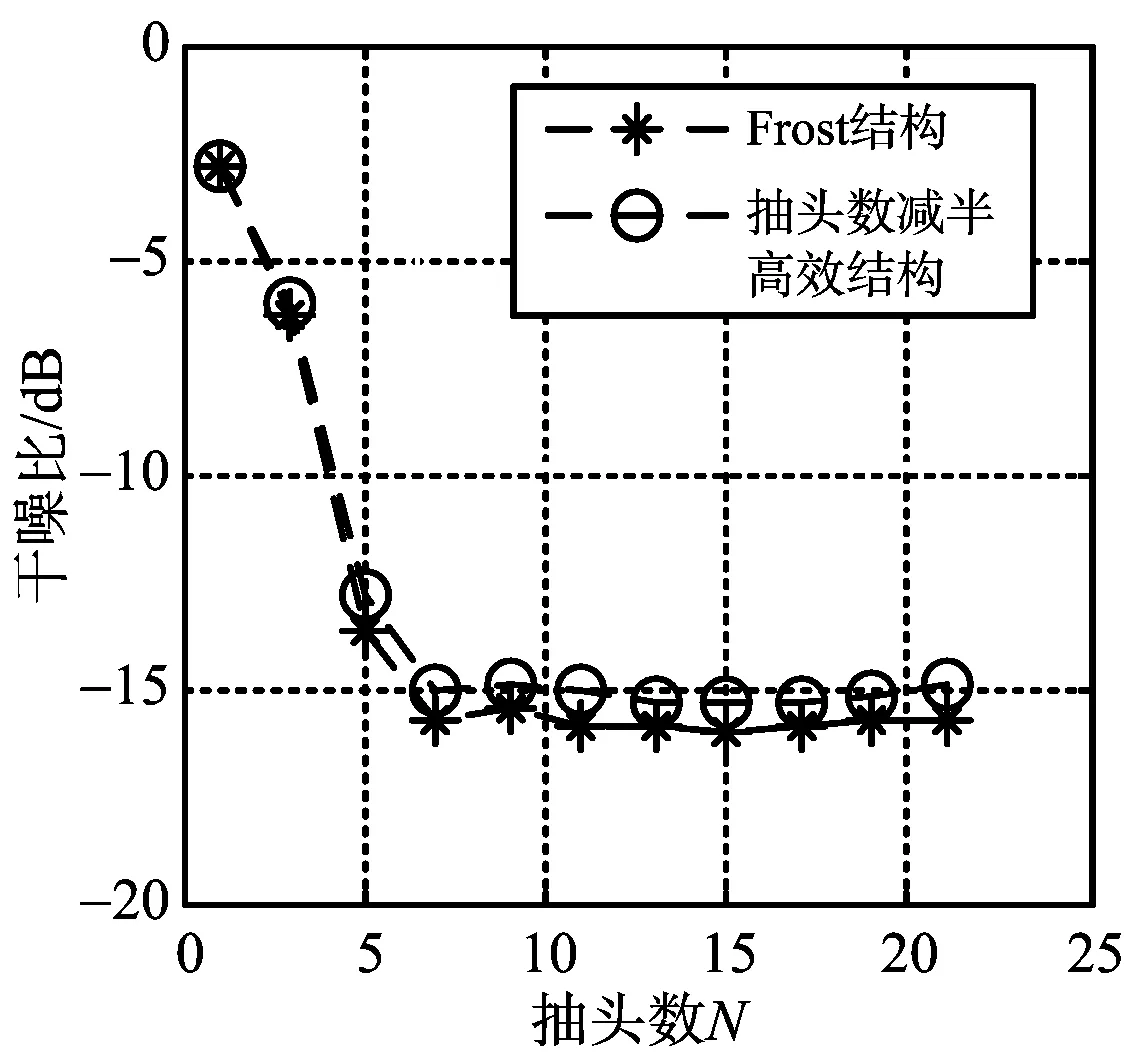
仿真實驗二 對比兩種結構陣元數對抗干擾能力的影響

信噪比SNR與陣元個數M有關，測試時需要用信噪比損失和信干噪比損失來進行結果分析。信噪比損失等于不存在干擾時信噪比與存在干擾的信噪比之差，信干噪比為不存在干擾時信干噪比與存在干擾信干噪比之差。保持抽頭數目不變，為N=7；分別選取M為偶數2,4,…,20，測試不同陣元個數在兩種結構下抗干擾后的信噪比(SNR)損失、干噪比(INR)和信干噪比(SINR)損失結果,如圖4所示。

(a) 陣元數對信噪比損失影響

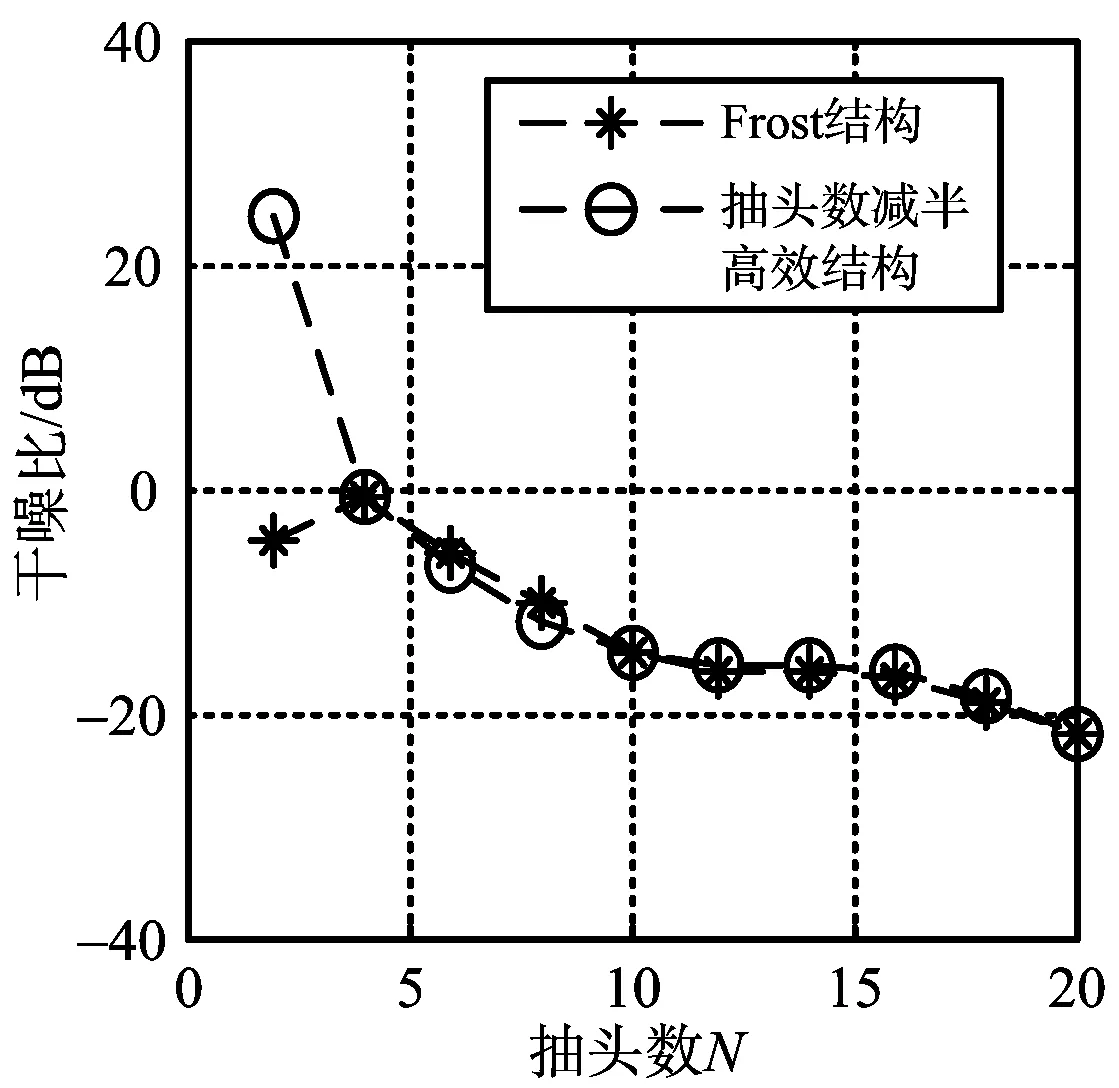
(b) 陣元數對干噪比影響

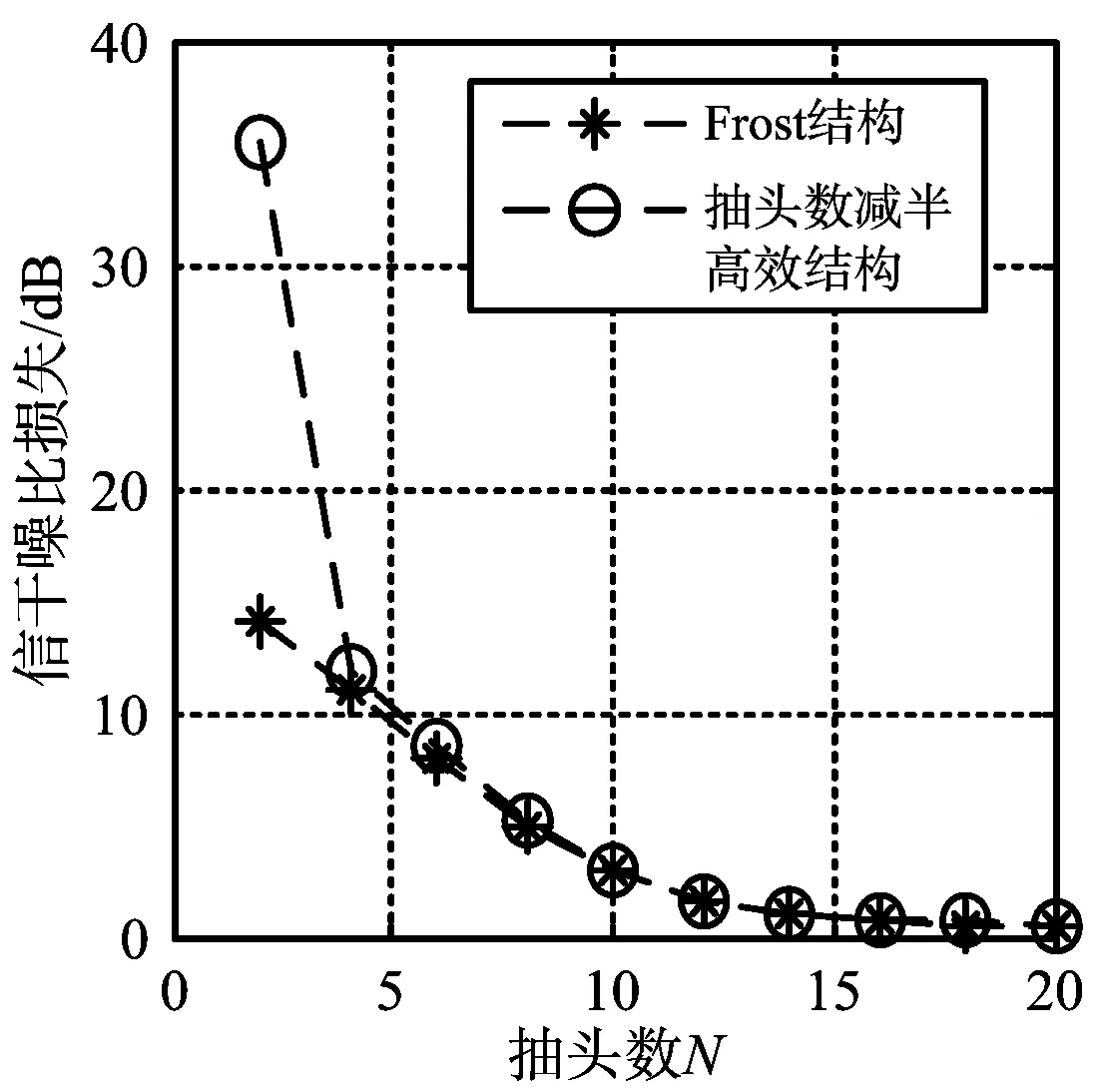
(c) 陣元數對信干噪比損失影響圖4 兩種結構下陣元數對抗干擾能力影響對比結果

圖4(a)顯示在不同陣元時Frost結構和改進結構的信噪比損失差異不大，證實了式(22)的正確性。常規結構和改進結構具有一樣的期望輸出功率，結構的不同導致了噪聲抑制不同，故兩者并不是完全重合。圖4(b)顯示M=2時常規結構遠小于改進結構的干擾剩余功率，此時改進結構干擾抑制結果較惡劣，干噪比比較高，仍剩余24.03 dB的干擾；而當陣元個數M≥4時，兩種結構干噪比幾乎無差。圖4(c)結果證實了式(28)、式(29)和式(30)的準確性，只是在M=2時，改進結構具有較差的抗干擾能力；M≥4時，抽頭減半結構與Frost結構具有一樣的剩余干擾功率。結構的不同導致了噪聲抑制不同，故兩者的干擾剩余存在輕微的差別。

通過兩個對比仿真實驗，當M≥4時，兩種結構的抗干擾能力幾乎無差，而改進結構在結構上減小一半抽頭數目亦可實現與Frost結構一樣的抗寬帶噪聲干擾能力，且運算量也大大減小。故而證實了該改進結構的可行性與高效性。

4 結束語

基于常規Frost空時結構，本文研究了一種改進的寬帶結構，在結構上將抽頭數目減至一半，權值數目與運算量可大幅下降。對改進結構抗寬帶噪聲干擾能力進行了理論推導，兩種結構具有一樣的輸出期望信號功率，M≥4(M為偶數)時抗干擾之后具有一樣的干擾剩余功率，細微差異是由于結構不同引起了噪聲干擾抑制的不同。仿真對比結果顯示改進結構并不會減弱抗干擾抑制性能，而是具有與Frost結構一樣的抗干擾能力。故抽頭減半的改進結構在保證抗干擾性能基礎上降低了空時維度和運算量，可應用于空時處理中，具有一定的高效性和可行性，但是本文僅提出了一種高效的可降低維度與運算量的改進結構，并沒有解決寬帶結構的最優問題，今后可作進一步擴展研究。