基于極限學習機的目標智能威脅感知技術

王永坤，鄭世友，鄧曉波

(1. 中國航空工業集團公司雷華電子技術研究所， 江蘇無錫 214063；2. 航空電子系統射頻綜合仿真航空科技重點實驗室， 江蘇無錫 214063)

0 引言

當前空戰決策仍依賴飛行員對各類傳感器獲取的多維態勢信息進行融合分析，并通過人為經驗進行目標威脅估計，進而完成作戰決策。這種傳統作戰方式下的感知與決策，一方面帶有人為主觀判斷，易引發戰場不確定性；另一方面，不利于加速OODA環的迭代，無法做到先敵發現、先敵攻擊。此外，下一代空戰環境的典型特點是無人化、智能化、體系化[1]。大型無人作戰飛機將是未來空戰的主角，智能化的目標威脅感知[2-3]作為大型無人作戰飛機自主空戰的關鍵支撐技術，是實現智能化空戰[4-5]的基礎。

針對未來智能化空戰的典型關鍵技術需求，目標威脅估計技術獲得了國內外學者的廣泛研究。目前國內外研究較多的目標威脅估計方法有多屬性決策法[6-7]、模糊邏輯法[8-11]、貝葉斯網絡法[12-14]以及神經網絡方法[15-17]等。多屬性決策法[6]首先需要設定影響威脅評估的各態勢因素固定權重值，不同的權重值設置對威脅評估結果有很大影響，算法魯棒性較差。模糊邏輯法[9]算法復雜性較高，不適于工程應用。基于貝葉斯網絡算法[12]的威脅估計重點在于推理估計各態勢因子對目標威脅度的影響概率，當態勢因子維度較高時，各影響因子的概率推理復雜度將會呈指數級上升。神經網絡方法[15-16]本質上屬于數據化方法，通常借助專家知識數據進行訓練建模，實現對目標威脅度的自主感知。但是，傳統的BP[17-18]神經網絡算法泛化能力有限，而且隨著樣本數增加，算法實時性將會大幅下降，無法做到在線學習。

極限學習機(Extreme Learning Machine, ELM)是由Huang等[19-20]提出的一種新型神經網絡算法，輸入權值和偏置量是隨機初始生成，輸出權值隨輸入權值和偏差的變化得到。該算法相比經典的BP神經網絡算法，首先具有學習速度快的優勢，此外，BP算法存在過度訓練的問題，使其泛化能力變差，而ELM具有較好的模型泛化能力，而且算法的高實時性使其廣泛應用于在線學習系統[21-22]。本文基于ELM算法進行空中目標威脅智能感知問題研究，首先對影響目標威脅度的態勢因子進行分析提取，并采用隸屬度函數[23]對各態勢因子進行歸一化數值解譯；然后，采用極限學習機對威脅估計的輸入輸出樣本數據進行訓練建模，最后采用多組測試樣本進行了與BP算法的對比仿真驗證。

1 威脅感知態勢因子提取

本文針對戰斗機空空作戰中的目標威脅感知問題進行研究，首先需要進行空中目標態勢因子的提取。在空戰中，目標的威脅屬性是基于飛機上各傳感器獲取的信息進行綜合判定，一般包括目標距離、速度、角度、機動性、目標類型、攻擊能力、情報信息等十多種態勢因子。但是在實際作戰中，由于計算資源和實時性的限制，無法融合所有維度的態勢信息進行威脅判定，因此，選擇權重屬性較高的態勢因子進行目標威脅綜合感知。

本文借助專家知識，從定性和定量兩個方面選擇高權重的態勢信息。針對定量因子，目標的距離和速度是從機載雷達可獲取的最直觀信息，也是進行威脅判定的基礎；此外，目標相對我方平臺的進入角也是需要考慮的一個重要因素，不同的進入角決定著敵方對我方實施攻擊的概率；再者，對目標探測的跟蹤精度是對敵方目標作戰意圖預測的重要基礎，而且較差的目標航跡質量大概意味著目標在作高機動運動，因此，目標的機動性也會影響對其探測的航跡質量。定性因子主要是目標類型，不同類型的目標具備不同的攻擊能力，是決定目標威脅的一個關鍵屬性。因此，空中目標威脅感知的態勢因子類型如圖1所示，集合為Tr={Tr1,Tr2,Tr3,Tr4,Tr5}={目標距離，目標速度，進入角，航跡精度，目標類型}。

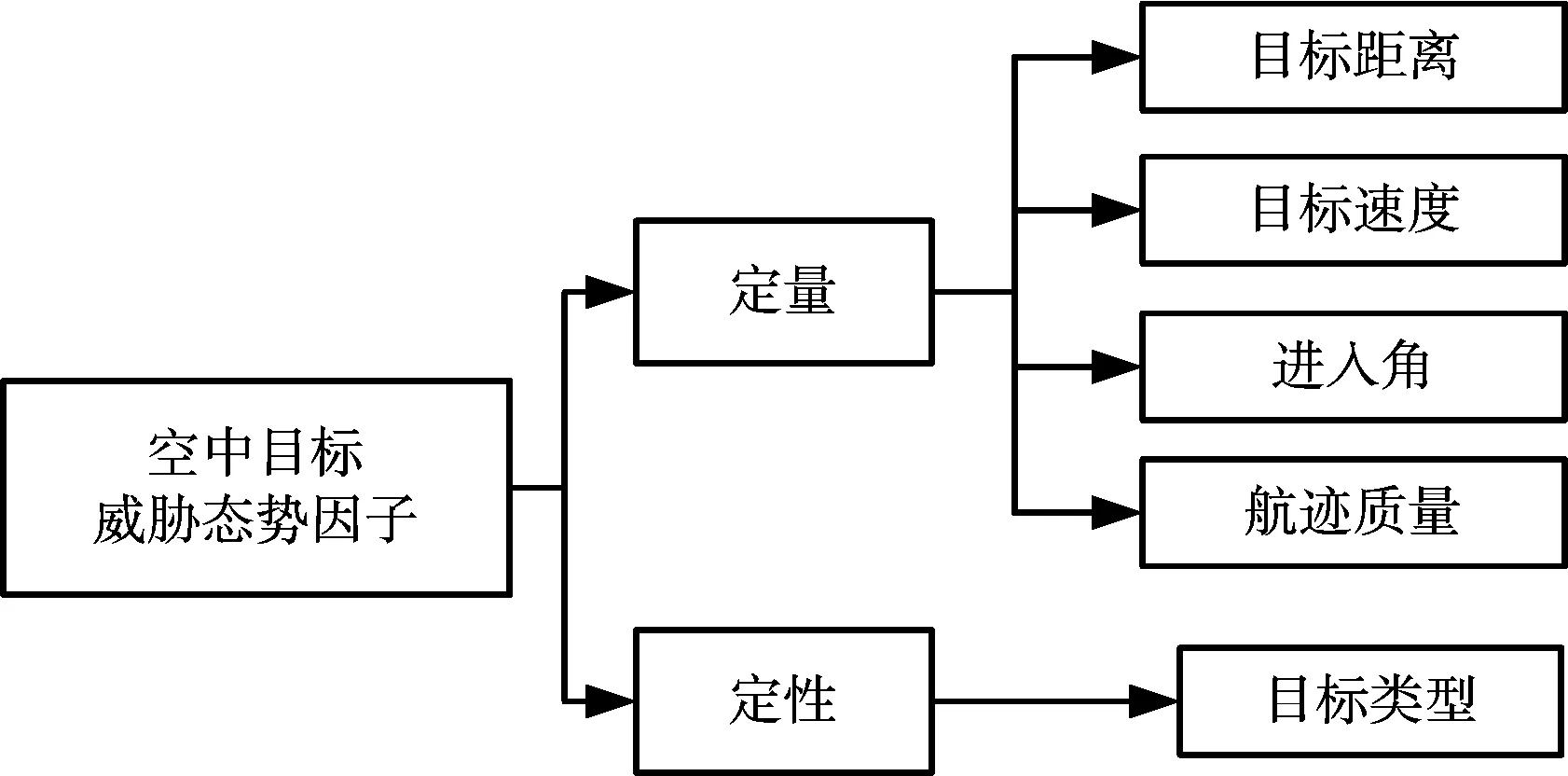
圖1 空中目標威脅態勢因子類型

2 基于模糊隸屬函數的態勢因子解譯

1) 目標距離隸屬度函數

目標距離信息由機載雷達獲取，距離越近，對我方平臺威脅度越大，因此，其隸屬度函數值應隨距離增加而單調下降。具體函數選取為

(1)

式中，a1=0.3R，a2=R，a3=1.15R，R是雷達探測距離,x1表示目標距離。

2) 目標速度隸屬度函數

戰斗機空戰過程中主要面臨亞音速飛機、超音速戰機以及超音速空空導彈等目標威脅，而高超聲速目標的攻擊對象一般不會是作戰飛機，因此，目標速度隸屬度函數符合中間型分布函數形式，在低速和超高速區函數值較小。具體函數選取為

(2)

式中，a=2 Ma，a1=0.5 Ma，a2=1.2 Ma，a3=2.5 Ma，x2表示目標速度。

3) 目標進入角隸屬度函數

目標進入角以我平臺與目標連線為基準，順時針方向為正。當目標進入角在-90°～90°區間時，函數值為正，且當目標進入角越接近0°，函數值越大。具體函數選取為

(3)

式中，k=3.5，x3表示目標進入角。

4) 目標航跡精度隸屬度函數

目標航跡精度隸屬度函數符合單調函數形式，對目標的跟蹤精度越高，越有利于對目標意圖的準確估計。因此，其函數值應隨跟蹤精度下降而單調上升。具體函數選取為

(4)

式中，k=2.75×10-5，a1=30，a2=300，x4表示目標跟蹤航跡質量。

5) 目標類型的隸屬度函數

戰斗機空戰中面對的目標類型包括各類作戰飛機以及敵機發射的空空導彈等，根據各類目標的攻擊能力不同，給定隸屬度函數如下：

(5)

3 基于極限學習機的目標威脅智能感知

本節基于極限學習機(ELM)算法進行目標威脅智能感知技術研究，通過對威脅感知的輸入輸出樣本數據進行學習建模，自主得到威脅感知結果，而不必進行繁瑣的權重調節步驟。

3.1 ELM算法原理

極限學習機是機器學習領域中的一種新型高效算法，以單隱層前饋神經網絡架構為基礎，通過高斯均勻隨機分布生成的固定權值矩陣實現輸入層到隱含層的連接，而隱含層與輸出層的加權矩陣的學習是ELM算法建模的主要目標。因此，ELM算法只需設置訓練網絡的隱層節點個數，不需要調整網絡的輸入權值以及隱層神經元的偏置。基于上述描述可知，ELM算法具備參數選擇容易、學習速度快的優勢。特別是在可用空戰數據樣本有限的條件下，能夠以零誤差逼近任意的線性和非線性函數。

極限學習機的具體算法原理如下：給定N個樣本(ui,ti)，其中ui=[ui1,ui2,…,uiNu]T和ti=[ti1,ti2,…,tiNy]T分別為樣本輸入輸出數據，Nx個隱層神經節點，Nx≤N，激活函數為h(u)的單隱層前饋神經網絡數學模型為

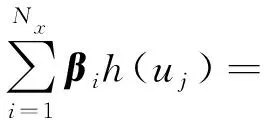
j=1,…,N

(6)

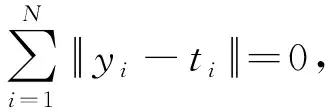
(7)

上述方程的矩陣形式為

Ηβ=T

(8)

式中，

(9)

H為極限學習機的隱含層輸出矩陣，其中第i列代表第i個隱層神經元關于每個輸入向量u1,u2,…,uN的輸出。

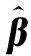
(10)

等同于求最小化全局誤差E：

(11)

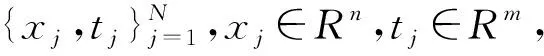
一般情況下，隱層節點數遠遠小于訓練樣本數，即Nx?N，因此需要求H的偽逆，即

(12)

式中，H?為隱含層輸出矩陣H的廣義摩爾逆[24]。當HTH非奇異時，H?=(HTH)-1HT，當HHT非奇異時，H?=HT(HHT)-1。根據嶺回歸原理[25]，求得的H?為

H?=(HTH+λI)-1HT

(13)

3.2 基于ELM的目標威脅智能感知

本文采用極限學習機技術實現空中目標智能威脅感知，首先選取輸入輸出數據，其中輸入數據為五維，包括目標距離、目標速度、目標進入角、目標類型以及目標航跡精度，輸出為目標的威脅度，并將樣本數據以一定比例劃分為訓練樣本和測試樣本，模型示意圖如圖2所示；然后，采用ELM算法對訓練樣本的輸入輸出數據進行訓練建模；訓練完成后，采用測試樣本進行結果測試，如果精度不滿足，重新訓練。

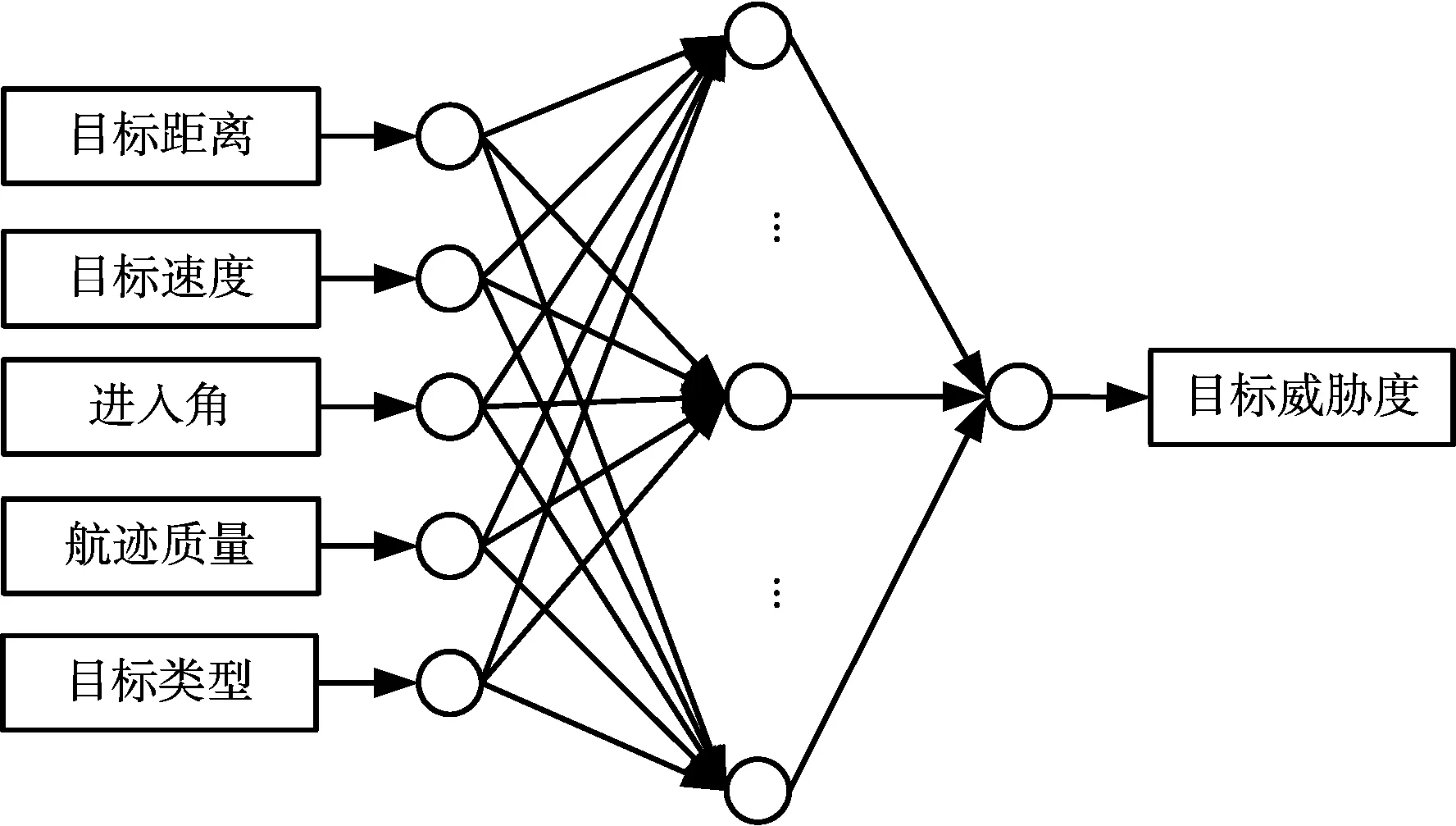
圖2 空中目標威脅ELM模型

具體步驟如下：

步驟1： 選取樣本數據，包括五維輸入樣本，目標距離特征、目標類型、速度、目標進入角以及航跡精度，輸出樣本數據即目標威脅度；

步驟2： 將樣本數據按一定比例劃分為訓練樣本和測試樣本數據；

步驟3： 選擇ELM算法進行建模訓練，由于本文研究問題屬于回歸問題，因此針對回歸問題設置ELM算法參數，即類型參數與隱層節點參數；

步驟4： 采用訓練樣本數據進行建模訓練；

步驟5： 采用測試樣本數據進行模型測試，精度滿足要求，則進入下一步，否則返回步驟3調整參數重新訓練；

步驟6： 結束。

4 算例分析與驗證

4.1 樣本數據選取

本節采用ELM算法對目標威脅估計進行特征建模，從而實現目標威脅智能感知。從某目標威脅數據庫選取目標威脅樣本數據，其中輸入樣本包括五維，即目標距離特征、目標類型、速度、攻擊角以及航跡質量，樣本選取策略如表1所示。

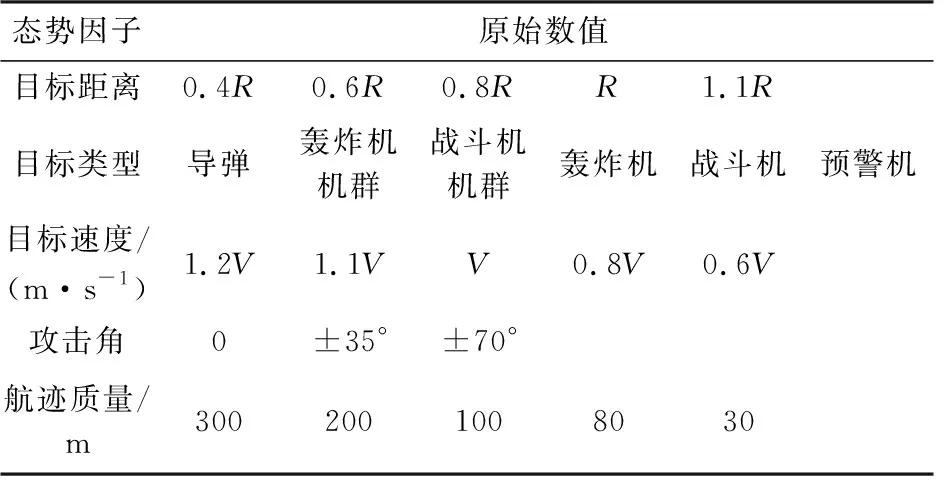
表1 目標威脅度輸入樣本

其中距離因子中的R=200 km，速度特征中的V表示聲速。各特征值的歸一化隸屬度函數計算結果如表2所示。

表2 輸入樣本的隸屬度函數值

通過上述數據預處理，選取的樣本數據共 2 250組。按均勻分布隨機抽取2 000組數據作為訓練樣本，250組數據作為測試樣本。

為了更好地說明采用ELM算法進行目標威脅感知的合理性，采用ELM和BP算法對比驗證。ELM采用隨機的方式設置輸入權值及隱層神經元的偏置，只需設置隱層神經元個數，設置為100；BP算法學習率設置為0.1，訓練目標1.0×10-5，隱層神經元個數同ELM算法。

4.2 仿真結果

首先選定2 000組樣本進行訓練，250組樣本進行測試。測試結果如圖3和圖4所示。從圖4統計的預測誤差百分比可知，ELM預測誤差基本在0.1%的水平，BP的誤差百分比約為0.5%，ELM大大低于BP算法的預測誤差百分比。此外，統計得到250組樣本中，ELM的預測均值誤差為5.0×10-4，BP的預測均值誤差為1.4×10-3。因此，基于ELM算法訓練得到的感知模型具有較高的威脅估計精度。

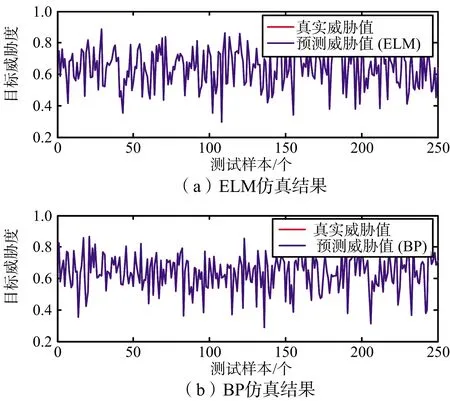
圖3 測試樣本目標威脅估計結果(250組)

圖4 目標威脅估計誤差百分比 (250組)

選定1 750組樣本數據進行模型訓練，500組數據作為測試，測試結果如圖5和圖6所示。ELM和BP的威脅估計均值誤差分別為5.2×10-4和1.6×10-3，ELM的估計精度較BP算法有一個量級的提升。

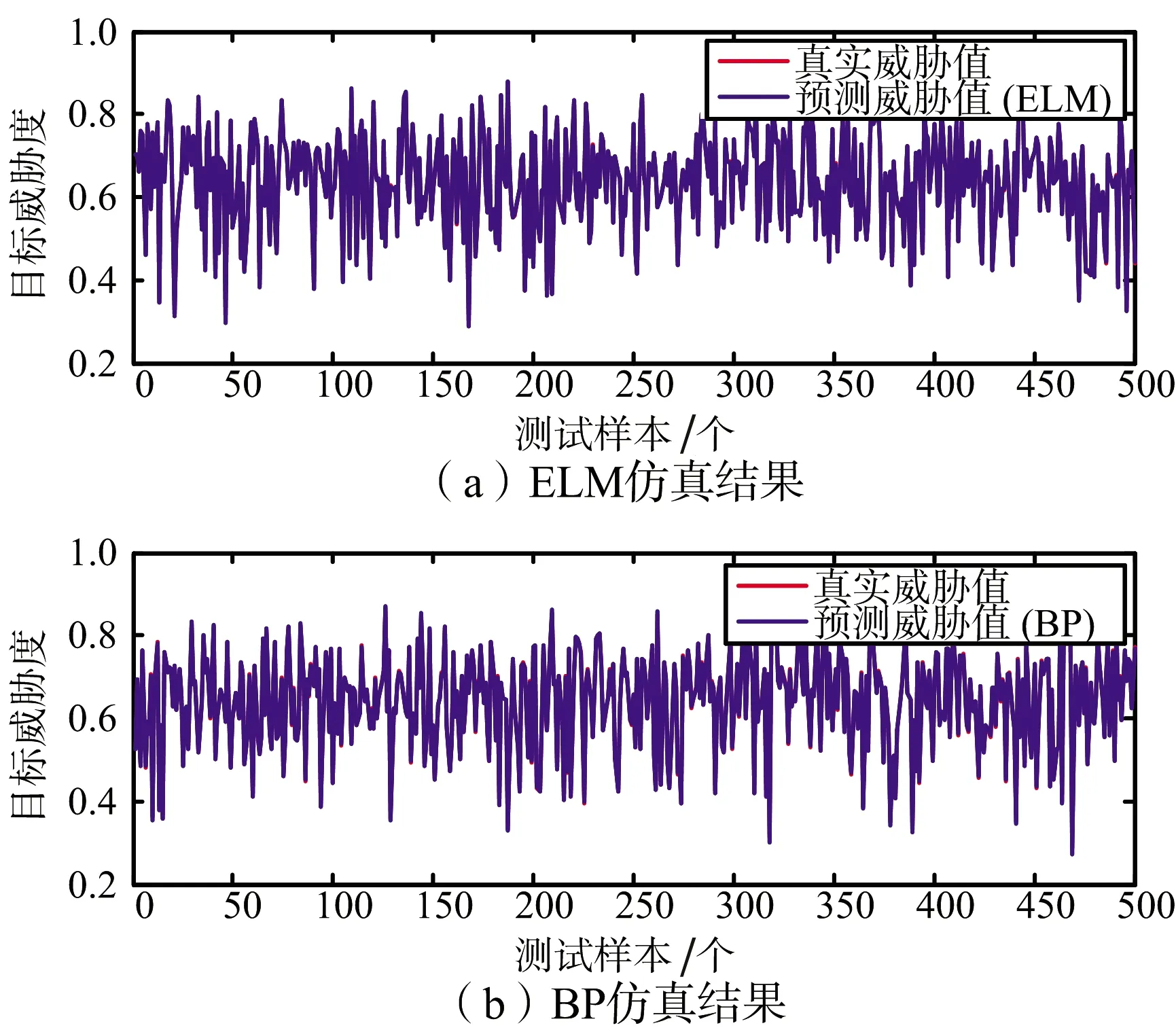
圖5 測試樣本目標威脅估計結果(500組)

圖6 目標威脅估計誤差百分比(500組)

選定1 250組樣本數據進行模型訓練，1 000組數據作為測試，測試結果如圖7和圖8所示。ELM和BP的預測均值誤差分別為7.02×10-4和1.87×10-3。

從以上三組仿真結果對比來看，不同數量的訓練樣本和測試樣本下ELM算法均具有較高的威脅感知精度。為驗證算法的學習速度和實時性，通過進一步的仿真，得到基于兩種算法進行目標威脅感知的對比結果，如表3所示。可以看出在不同的訓練樣本數量下，ELM訓練出的感知模型均具有較高的估計精度，相較于BP算法存在一個量級上的精度提升；而且更為重要的是，在同等訓練樣本數目下，ELM的訓練時間要比BP算法低一到兩個數量級，這對于實時性要求很高的威脅感知系統非常重要。

圖7 測試樣本目標威脅估計 (1 000組)

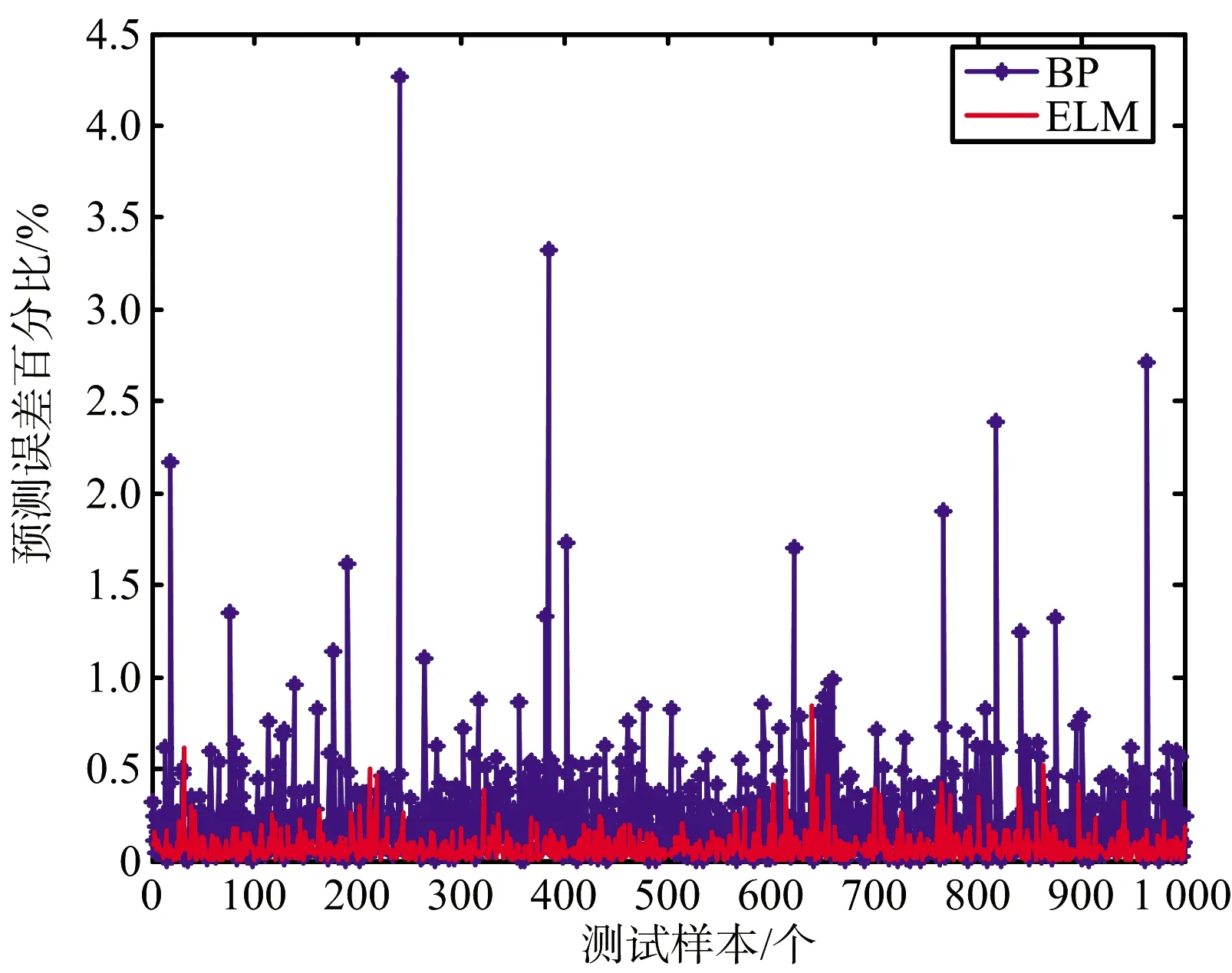
圖8 目標威脅估計誤差百分比(1 000組)

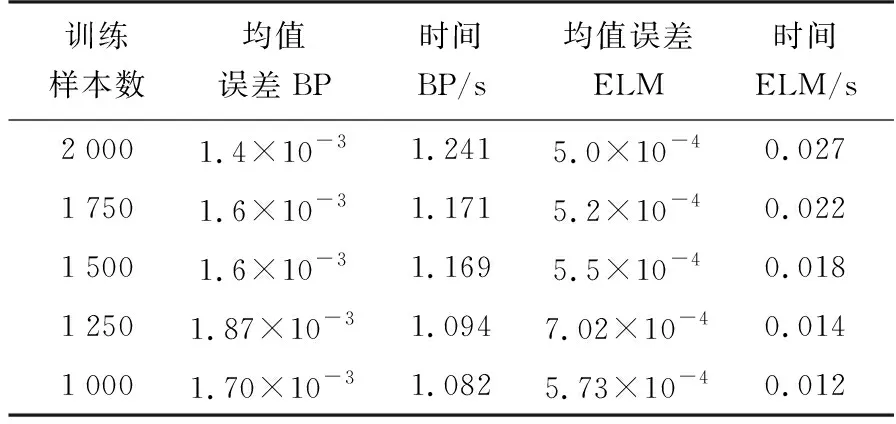
表3 BP和ELM算法對比

5 結束語

空中目標威脅感知是空戰中作戰決策的關鍵依據，涉及的態勢因素眾多且融合邏輯復雜。本文基于專家知識綜合考慮空中目標的特點、類型以及威脅屬性多重因素，并采用一種高性能機器學習算法—極限學習機進行目標威脅估計建模，從而實現空戰環境下各類目標威脅度的實時智能感知。通過選取不同數量的測試樣本數據，基于ELM算法和BP神經網絡算法進行了威脅感知的對比仿真，結果均驗證了ELM算法訓練出的感知模型具有較高的威脅估計精度和良好的實時性。