在小學數學教學中滲透模型思想的研究

朱璐璐

摘? 要：模型思想是數學的三大基本思想之一，它是數學與外部世界溝通的橋梁，體現了數學廣泛的應用性。數學模型是數學應用和問題解決的核心。我們可以通過兩種途徑培養學生的模型思想：第一，指導學生學習基本數學模型;第二，指導學生使用基本數學模型進行問題解決。

關鍵詞：模型思想;問題解決;子模型;母模型

“模型思想”是《義務教育數學課程標準（2011年版）》中新增的一個核心詞。數學模型在當今信息化社會中已經有十分廣泛的應用，在大學、中學也有比較深入的研究和實踐，但是在課標修訂之前，小學數學教師很少踐行數學建模。如何培養小學生的“模型思想”，還有很多問題值得探討。

在小學階段，從課程標準的角度正式提出“模型思想”，表明了模型是數學應用和問題解決的核心。我們可以通過兩種途徑培養學生的模型思想：第一，指導學生學習基本數學模型;第二，指導學生使用基本數學模型進行問題解決。

一、指導學生學習基本數學模型

學生學習基本數學模型的過程可以是接受學習，也可以是探究過程。在這里筆者重點闡述探究過程，即經歷類似于數學家建模的再創造過程。鑒于小學生的認知水平，小學大部分公式、定理的推導大都采用不完全歸納法，這樣的做法值得商榷。數學是思維的科學，培養學生的推理能力也應該在公式、定理的推導上得到一定的體現。

例1：乘法結合律的推導。橫著看，每行有6個人，一共4行，一共有6×4人，每人拿著3個氣球，因此有3×（6×4）個氣球;或者橫著每行有3×6個氣球，一共有4行，因此有3×6×4個氣球。因此，3×（6×4）=3×6×4。學生很容易就發現，將數字變一下，這個推導過程依然成立。通過推理，學生再創造了“乘法結合律”。

二、指導學生使用基本數學模型進行問題解決

模型是解決一類問題的優化方案，是前人總結出來的有效方法。教師指導學生使用基本數學模型進行問題解決的過程類似于數學建模過程，即“問題情境——建立模型——求解驗證”的過程。利用模型求解就是站在巨人的肩膀上進行問題解決，是學生舍棄非本質要素對現實或者直觀情境的本質要素進行抽象，之后建立模型對問題進行數學化，最后通過數學特定的解題方式進行求解的過程。

例2：同學們一起去游園，有48人，每輛大車租金120元，限乘12人，每輛小車租金160元，限乘18人。可以怎樣租車？需要多少錢？

我們班有個孩子是這樣做的（見圖2）。通過與他溝通，發現他的想法是：先考慮全部租小車，需要4輛;后考慮全部租大車，2輛大車不夠坐，需要3輛大車;大車、小車都考慮，就需要1輛大車搭配1輛小車。因此，只有三種方案。學生的思路在“大小車都租”這里出了問題，大車和小車的輛數并不一定相同。

我們一般用列表模型解決這個問題。先假設全部租大車，然后將大車輛數依次減一，求小車的輛數，之后求出可乘人數和租金（見表1）。學生借助列表法這種經過前人整理優化的模型，可以快速梳理出多種租車方案，并從中選擇自己想要的方案，不容易出現思維誤區。

例3：雞兔同籠，有5個頭，14只腳，那么雞兔各有多少只？

這個問題同樣可以用列表模型有條理地解決問題（見表2）。

表2

（單位：只）

通過這兩個例子，我們發現列表模型使我們的思路更清晰，它能幫助我們進行有序的、不重復、不遺漏的思考。因此可以認為，模型是解決一類問題的有效方案。

三、重視模型的內在關聯

根據信息加工理論，進入短時記憶的信息，如果得到復述，將可以進入長時記憶，否則將被遺忘。這里的復述更多指的是精細復述，精細復述是指將信息進行分析使之與已有的知識經驗建立起某種內在聯系。同時雖然長時記憶的信息提取受很多因素影響，但是有意編碼（把輸入的信息與存儲的知識聯系起來）的效果優于自動編碼（不需注意和意志努力）。因此，將新學習的模型與已學的模型建立聯系，是保持記憶和提高提取信息效率的有效方法。

為了便于記憶和信息的提取，筆者將有本質聯系的模型進行了梳理、歸納。下面筆者將介紹四種基本模型，分別是：“加法”模型、“減法”模型、“乘法”模型、“除法”模型，每種模型都可以細分為多個子模型，下面將展開詳細說明。

1. “加法”模型

（1）數平行線

例4：數一數，下邊圖形中有幾組平行線？

橫著看有2條互相平行的直線，因此只有1組平行線;

斜著看有5條互相平行的直線，因此有4+3+2+1=10（組）平行線;

一共有1+10=11（組）平行線。

（2）數線段

例5：數一數，下邊圖形中有多少條線段？

先數基本線段，有4條。因此，線段總共有4+3+2+1=10（條）。

（3）數角

例6：數一數，下邊圖形中有多少個角？

先數基本角，有4個。因此，角總共有4+3+2+1=10（個）。

（4）數三角形

例7：數一數，下邊圖形中有多少個三角形？

先數基本三角形，有4個。因此，三角形總共有4+3+2+1=10（個）。

（5）數長方形

例8：數一數，下邊圖形中有多少個長方形？

先數基本長方形，有4個。因此，長方形總共有4+3+2+1=10（個）。

（6）數直線

例9：經過下邊任意兩點畫直線，可以畫多少條？

先找一個點，它可以與其他四個點連4條直線，再考慮其他點。因此，直線總共有4+3+2+1=10（條）。

以上6個子模型用相同的方法解決問題，因此它們可歸為同一母模型。在小學階段，我們把這種方法叫作枚舉法。但是在中學，這種方法叫作排列組合。它屬于組合中的C■模型。如何證明呢？我們知道C■=■=■（以例9為例，這里的n指的是5個點），而用枚舉法解題公式是（n-1）+…+3+2+1，用配對求和的方法可知（n-1）+…+3+2+1=（n-1+1）×■=■。

由于從形式上看，上面的式子都是用加號連接，因此，簡稱為“加法”模型。

2. “減法”模型

（1）用斷尺測量物體的長度

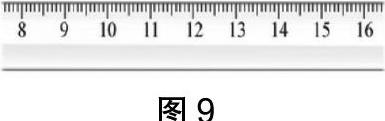
例10：怎樣用下邊的“斷尺子”畫出一條長6厘米的線？

16-10=6（厘米）;15-9=6（厘米）;14-8=6（厘米）。

我們發現：兩個刻度之間的距離=最后面的刻度-前面的刻度。

（2）求經過的時間

例11：淘氣早上6時30分起床，7時40分上學，他從起床到上學一共用了多長時間？

7時40分-6時30分=1時10分。

例12：第29屆夏季奧林匹克運動會于2008年8月8日20時在北京開幕，至8月24日20時，共歷時______天。

24-8=16（天）。

我們發現：經過的時間=后面的時刻-前面的時刻。

（3）求用電量

例13：請算出樂樂家7月份的用電量。

545-430=115（千瓦時）。

我們發現：這個月的用電量=這個月的讀數-上個月的讀數。

以上4個例題都是在求相差數，而“相差數=大數-小數”。這些模型都可以認為是在一維空間求相差數，并且都是起始數值不為0的情況，更能體現相差數的意義。

大數和小數之間的差距，還可以等同于植樹問題的“求幾段”“求間距”，即數間隔模型。

（4）求面積差

例14：分別求以下三種圖形的陰影部分的面積。

三個圖形的陰影部分都是不規則圖形，但是它們的面積都是“大長方形的面積-小長方形的面積”（即面積差）。

除了在一維空間求相差數，在二維空間也可以求相差數，求面積差就屬于這種類型。而且通過三種圖形的對比，學生在靜態圖中感受到了動態地變化，同時感受到無論圖形如何變化，三張圖的本質是一樣的，領悟到了“變中的不變”。

由于從形式上看，上面的式子都是用減號連接，因此，簡稱為“減法”模型。

3. “乘法”模型

（1）“總價=單價×數量”模型

例15：單價10元的皮球，小明買了8個，一共花了多少錢？

10×8=80（元）。

答：一共花了80元。

（2）“路程=速度×時間”模型

例16：曉東從學校到少年宮一共用了10分鐘，他每分鐘走60米，從學校到少年宮的路程是多少米？

60×10=600（米）。

答：從學校到少年宮的路程是600米。

（3）“多倍數=1倍數×倍數”模型

例17：紅阿姨到超市買了8個雞蛋，黃阿姨買的雞蛋是紅阿姨的5倍，那么黃阿姨買了幾個雞蛋？

8×5=40（個）。

答：黃阿姨買了40個雞蛋。

（4）度量模型

例18：下面是體育館的一個看臺，大約有多少名觀眾？

可能出現多種方法，如可以將這個看臺分成3部分，每部分有8行，因此每部分有7×8=56（人），3部分一共有7×8×3=168（人）。

本問題解決的策略是“化整為零”，即把體育場的觀眾分成數目大體相同的幾個部分，想辦法估計出其中一個部分的數量，就可以用乘法估算整個體育場觀眾的數量。

例19：估一估，下面的角有多少度？

我們把∠1看成一個標準，則∠2大約有3個∠1，大約30°;∠3大約比直角少一個∠1，大約80°。

對大數的估計或者對角度的估計的思想，就是度量思想。要先確定一個度量單位（標準），再數出單位數（有幾個標準），就可以用乘法算出總量（角度）。

上面的這4個模型都是求“幾個標準”的問題，都可以歸結為“總數=每份數×份數”這一數學“乘法”模型。

4. “除法”模型

（1）雞兔同籠問題

兔數=（總腳數-雞腳數×總頭數）÷（兔腳數-雞腳數）。

（2）追及問題

追及時間=追及路程÷速度差。

（3）贏虧問題

兩次分配結果的差（贏+虧）÷兩次分配數量的差=份數。

通過分析我們發現，上面的三個模型都可以歸納為“相差數÷每份數的差=份數”的“減法”模型。

這些數學模型是學生經常遇到的問題，也都有各自的公式，但是我們發現，看似不一樣的數學問題，對其進行二次抽象會發現它們的數學模型（結構）是一樣的。教師在指導學生學習基本模型時，如果可以在適當的時機對學生進行“點撥”，對公式進行一定的歸納提升，幫助學生認清知識點之間的本質聯系，將新知識整合到已有的知識框架中，學生的學習將更能夠融會貫通、事半功倍，也能促進信息在人腦中的保持和提高提取信息的效率。這里需要補充的是，雖然這些“子模型”都可以歸納為同一種“母模型”，本質是相同的，但是由于“母模型”太過抽象，更具一般性，而“子模型”比較容易推導，更好理解，有它的特殊性。因此，對于學生來說，循序漸進，先學習具體的（子模型），再體會它們都可以歸納為抽象的（母模型），是比較合理的。

模型思想是數學的三大基本思想之一，它是數學與外部世界溝通的橋梁，體現了數學廣泛的應用性。數學模型是數學應用和問題解決的核心。如何培養學生的模型思想前路漫漫，還有很多值得研究的地方。