論直觀之形在小學數學運算中的運用

張金梅

摘? 要：小學生的思維方式受年齡和心理特征的影響，以形象思維占主導。因此，不少學生在遇到抽象的數學概念或運算時，常出現空間想象力缺乏、辨認困難等障礙。而運算是最基本的數學能力之一，教師該如何引導學生以直觀之形為基礎，逐漸掌握并運用運算定律，形成有序思考問題的習慣呢？文章就這個問題談一些想法。

關鍵詞：直觀之形;運算;思維

數學的直觀之形一般指直觀可見的內容，具有直觀性、形象性等特征，基本歸屬于經驗幾何的范疇，以幾何與圖形的方式呈現。數學運算是小學數學教育的重要內容之一。針對小學生的身心特征和思維方式，怎樣利用直觀之形協助數學運算的教學，是我們每個專業教師值得思考的問題之一。學生可通過觀察、操作直觀之形增加感知，然后在此基礎上比較、分析并總結，從而掌握運算方法，形成較好的數學思維，這是一個從具體到抽象的過程。

一、數學之形與運算的關系

小學階段認識整數、分數和小數等知識，無不以運算這條主線貫穿整個過程，而其他的一些內容則是圍繞運算這條主線而展開。仔細研讀數學教材，會發現編者安排的各部分內容、習題以及思考題等，都尊重了學生的認知發展規律，借助了大量的圖形或生活實例讓學生通過直觀的數學之形更好地掌握運算方法。

1. 借助直觀之形，理解運算意義

從發展心理學角度出發，低年級學生以直觀形象思維為主，對抽象的運算意義難以理解。對于一二年級的學生來說，乘法的概念過于抽象，憑純粹的理論，大部分學生難以理解其真正的內涵。若借助直觀的數學圖形，則能一目了然地看出加法與乘法之間的關系。因此，在一二年級的教材中只安排了整數四則運算的內容。便于學生依托直觀生動的實際圖形或物體展開思考，通過直觀的感知和身臨其境的操作將數與數合在一起進行運算。

例1：以“乘法的初步認識”為例（見圖1）。

圖形組合讓學生對加法和乘法有了更直觀的認識，突出相同數字連續相加和乘法的運算關系。學生在“3”和“5”兩個數的連續相加中，會自然而然地使用幾個“3”或幾個“5”相加的言語表達數量關系，完成從圖形到語言，再到抽象化概念的過程，乘法運算的定義也自然而然地生成。

2. 借助直觀之形，理解運算算理

學生運算能力的強弱取決于運算方法的掌握和算理的理解程度。算理就是運算的原理，它是運算方法的基礎。若沒有理解算理，就無法真正掌握算法，更談不上運算技能。因此，教師要引導學生將算法與算理有機地融合，遇到題目不僅會運算，還明白這么算的原因是什么。為了讓學生真正地理解算理，教材中也精心選擇了一些直觀可操作性的圖片和材料（小棒、圖形、錢幣等），學生借助這些直觀可見，具有可操作性的“形”，加上已有的知識經驗，將抽象化的算理轉變為直觀具體化容易理解的內容。

例2：以“100以內加減法豎式計算”為例（見圖2）。

教材選用了直觀便于操作的小棒，讓學生在圖形中找出抽象的豎式關系，從而明確豎式計算的對齊方法以及同位數才可以相加的規則。學生通過形和數的轉化，實現直觀思維向抽象思維的轉化。

3. 借助直觀之形，提升運算能力

想提高學生的運算能力，離不開運算練習，而枯燥單一的運算練習，很容易讓學生的思維陷入僵化的狀態。根據這個特點，教材編排時，增加了不少的數形內容，為學生提供更多的思維空間，以豐富運算練習，提升運算能力。

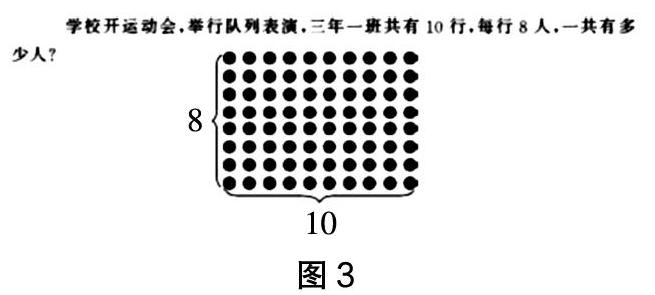
例3：以“兩位數乘一位數”章節中一道練習題為例（見圖3）。

通過圖形理解“10×8”這個算式，比單純的理論更直觀，學生通過自己的知識經驗和思維能力，閱讀圖形就能給出相應的算式。算式與圖形的互譯讓學生學會讀圖，理解算式的真正算理，結合圖形從多角度思考問題，不知不覺中就提升了運算能力。

二、數學之形在運算中的作用

1. 以形助教，發展抽象思維

孔凡哲曾說過：“小棒類的圖形或實物屬于最直接的直觀抽象，它能體現出數學對象之間的關系與屬性。”心理學家研究發現，小學階段低年級的學生想要理解數學運算，需借助實際物品逐漸轉向替代物完成抽象;小學中年級的學生逐漸淡化實物的直觀化，轉向于幾何圖形來理解數學運算;而小學高年級的學生則更注重于數與形之間的關系，通過現象獲得運算的本質。由此可見，小學生的思維隨著年齡的增長和知識儲備的豐富，會發生相應的變化。教師在教學過程中，應因材施教，根據實際情況對教學方案靈活地進行調整。

例4：以“運算律”的教學為例（見圖4）。

運算律的教學，可根據學生思維的發展水平，借助其生活情境及抽象程度稍高一些的圖形直觀、動態的演示，引導學生掌握運算律。例如，“加法交換律”，可以在實數直線上表示數“a”和數“b”，使用箭頭演示a+b和b+a的動態。學生可在實數直線上觀察到這兩個加法的變化與位置無關;兩個加數的位置交換，和依然不變。

例5：以“表內乘除法”的教學為例（見圖5）。

學生從圖5的設計可獲得正方形圖形和運算之間的聯系和各個算式之間的關系。這張圖帶給學生以下信息：乘法算式和正方形圖是有關系的;不同顏色的小方格可列出加法算式;一幅圖可列出兩種算式。教師引導學生比較加法算式和乘法算式，思考同一幅圖為什么會列出不一樣的算式，這兩個算式之間的關系是怎樣的，他們之間有什么樣的聯系。學生在比較和思考中逐漸感知加法和乘法算式兩者的內在聯系，圖形與運算相結合的方式，對學生抽象思維的發展起到明顯的促進作用。

2. 以形助教，獲得數形結合的感悟

直觀之形廣泛地運用于數學運算中，不但幫助學生理解了抽象的數學定義、法則和算理，還是學生形成良好數形結合感悟的媒介。以形助教是小學數學運算教學的方法，學生在直觀之形和算式之間建立聯系，逐漸完成形象思維向抽象思維的過渡。教師在使用以形助教過程中要根據學生的心理特征和認知發展規律，用恰當的方法在適當的時候呈現具體的直觀之形，巧妙地將直觀之形和算式之間建立聯系，達到以形助運算之效。

例6：以“表內乘法”中的一道思考題為例（見圖6）。

此題的目的在于讓學生通過觀察，構建“圖形——數字——算式”的模型，根據圖中的規律，獲得數形結合的感悟。

例7：“解決問題的策略”中的一道習題（見圖7）。

學生對正方形和數都有了一定的感知后，根據形與式的關系，逐漸形成數形結合的思想。

3. 以形助教，發展數學思維

學生通過直觀之形的觀察與操作，形成新的認知后，教師需根據學生的身心發展特征，引導學生從多角度出發，將直觀的形和抽象的運算緊密結合，使用各種方式加以表征，逐步形成“動作思維——形象思維——抽象思維”的過渡。

以“100以內的加減法”為例，學生在使用小棒擺放的過程中，教師可根據學生年齡特征，引導學生表達操作過程。如鼓勵低年級的學生邊操作邊表述，學生不知不覺就將直觀操作的經驗遷移到運算中，從而理解算理，完成算法。針對中、高年級的學生，可在語言表征的同時引入一些符號圖形，鼓勵學生加以表征。如高年級的“分數乘法”內容的教學，教師可先將乘法算式呈現給學生，鼓勵學生根據分數的意義使用圖形來演繹算式的意義，再根據圖形分析分數乘法運算的算理，反復多次以后，用字母符號概括出分數乘法運算的規律。學生在此過程中，逐漸形成新的數學思維。

蘇娜丹戴克曾說過：“若告訴我，我會忘記;若給我看，我會記住;若讓我參與，我會理解。”只有經過學生加工內化的知識，才是屬于學生自己的知識。在數學運算教學過程中，教師可借助教材或生活中的各種直觀之形，組織學生通過言語表達，形成有序思考的能力，實現低思維水平到高思維水平的過渡。