隨機(jī)強(qiáng)偽壓縮算子多步迭代序列的收斂性

聶 輝，張樹義

（渤海大學(xué) 數(shù)理學(xué)院，遼寧 錦州121013）

1 引言和預(yù)備知識(shí)

隨機(jī)不動(dòng)點(diǎn)問題廣泛應(yīng)用于生物、物理和經(jīng)濟(jì)等領(lǐng)域.文獻(xiàn)[1-8]對(duì)隨機(jī)不動(dòng)點(diǎn)理論進(jìn)行了廣泛研究，其中，文獻(xiàn)[1-2]在可分的Hilbert空間中研究了隨機(jī)算子方程解和隨機(jī)算子不動(dòng)點(diǎn)隨機(jī)Mann迭代序列的收斂性，文獻(xiàn)[3]在值域有界的一致光滑可分的Banach空間中研究了一類隨機(jī)強(qiáng)偽壓縮算子隨機(jī)不動(dòng)點(diǎn)的Ishikawa迭代序列的逼近問題.另外，文獻(xiàn)[9-17]研究了包括廣義Lipschitz算子在內(nèi)的幾類非線性算子不動(dòng)點(diǎn)迭代的逼近問題，文獻(xiàn)[18-24]研究了幾類非線性映象不動(dòng)點(diǎn)多步迭代算法的收斂性.受上述工作啟發(fā)，本文用廣義Lipschitz取代值域有界條件，在可分Banach空間中研究一類隨機(jī)強(qiáng)偽壓縮算子隨機(jī)不動(dòng)點(diǎn)的多步隨機(jī)迭代序列的逼近問題，建立了隨機(jī)強(qiáng)偽壓縮算子隨機(jī)不動(dòng)點(diǎn)的多步隨機(jī)迭代序列的強(qiáng)收斂性定理.由于值域有界一定是廣義Lipschitz的，而反之未必成立[13]，因此本文推廣和改進(jìn)了相關(guān)文獻(xiàn)中的結(jié)果.

假設(shè)（Ω，∑）為一可測(cè)空間，∑是Ω的σ-代數(shù).E為一致光滑的可分Banach空間，E*為E的對(duì)偶空間，C為E的非空閉凸子集，正規(guī)對(duì)偶映象J：E→2E*為

定義1[3]（1）稱函數(shù)f：Ω→C為可測(cè)的，如果對(duì)任意Borel子集B，有f-1（B∩C）∈∑.

（2）稱T：Ω×C→C為隨機(jī)算子，如果對(duì)任一x∈C，T（·，x）：Ω→C是可測(cè)的.

（3）稱可測(cè)函數(shù)f：Ω→C為隨機(jī)算子T：Ω×C→C的隨機(jī)不動(dòng)點(diǎn)，如果對(duì)任意ω∈Ω，有T（ω，fω）=f（ω）.

（4）稱隨機(jī)算子T：Ω×C→C為連續(xù)的，如果對(duì)任意給定的ω∈Ω，T（ω，·）：C→C是連續(xù)的.

引理1[8]設(shè)E為可分的距離空間，Y為距離空間.T：Ω×E→Y在ω∈Ω是可測(cè)的，并且在x∈E是連續(xù)的.如果g：Ω→E是可測(cè)函數(shù)，則f（·，g（·））：Ω→Y是可測(cè)的.

定義2設(shè)Ti（i=1，2，…，s）：Ω×C→C為s個(gè)連續(xù)的隨機(jī)算子，x0：Ω→C是任意給定的可測(cè)函數(shù)，定義序列{xn（ω）}為

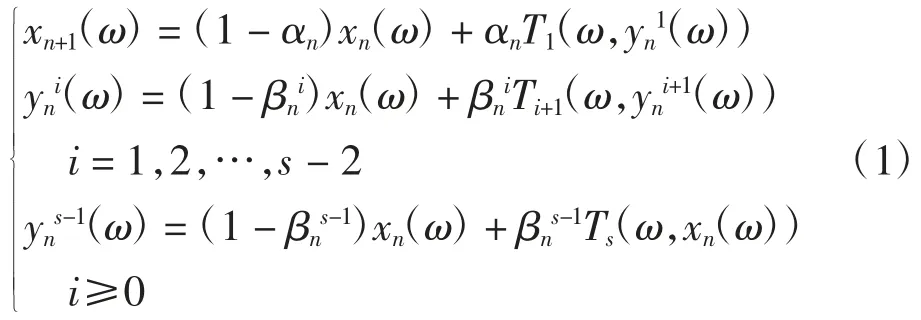
稱序列{xn（ω）}為隨機(jī)多步迭代序列，其中[0，1]，i=1，2，…，s-1.

在定義2中取s=2，對(duì)每一ω∈Ω，令T1（ω，·）=T2（ω，·）=T（ω，·），便得到文獻(xiàn)[10]中的隨機(jī)Ishikawa迭代序列

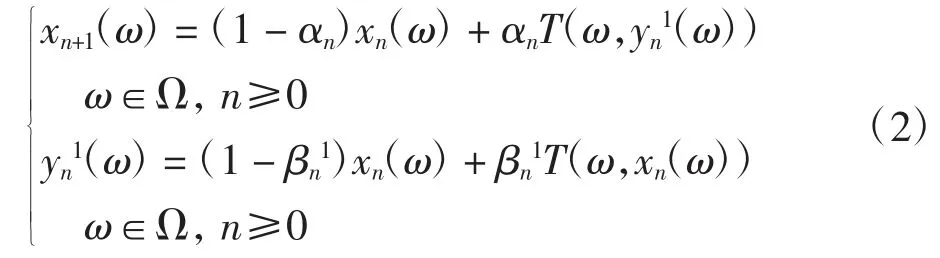
注1Ti（i=1，2，…，s）：Ω×C→C是連續(xù)的隨機(jī)算子，C是E的非空閉凸子集，x0：Ω→C是可測(cè)函數(shù).由引理1易知{xn}和{yni}（i=1，2，…，s-1）是Ω到C的可測(cè)函數(shù).

定義3[3]（1）稱隨機(jī)算子T：Ω×C→C為強(qiáng)偽壓縮的，如果存在函數(shù)k：Ω→（0，1），對(duì)任意x、y∈C，存在j（x-y）∈J（x-y），使得對(duì)每一ω∈Ω，有

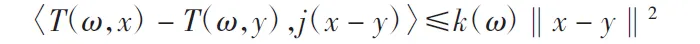
（2）稱隨機(jī)算子T：Ω×C→C為強(qiáng)增生的，如果存在函數(shù)h：Ω→（0，1），對(duì)任意x、y∈C，存在j（x-y）∈J（x-y），使得對(duì)每一ω∈Ω，有

注2T：Ω×C→C是具有函數(shù)k：Ω→（0，1）的強(qiáng)偽壓縮算子，當(dāng)且僅當(dāng)I-T是具有函數(shù)h：Ω→（0，1）的強(qiáng)增生算子，其中h（ω）=1-k（ω）.

下面將廣義Lipschitz算子擴(kuò)展到隨機(jī)算子的情形.

定義4稱隨機(jī)算子T：Ω×C→C為廣 義Lipschitz的，如果存在常數(shù)L≥1，使得對(duì)任意x、y∈C，對(duì)每一ω∈Ω，有

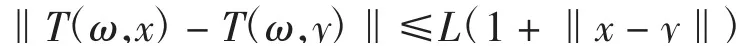
注3文獻(xiàn)[13]指出：值域有界的隨機(jī)算子一定是廣義Lipschitz的，而反之未必成立.

引理2[9]設(shè)E為實(shí)Banach空間.

（1）如果T：E→E是連續(xù)的強(qiáng)偽壓縮算子，則T有唯一不動(dòng)點(diǎn).

（2）如果T：E→E是連續(xù)的強(qiáng)增生算子，則對(duì)f∈E，方程Tx=f有唯一解.

引理3[3]設(shè)E為實(shí)Banach空間，J是正規(guī)對(duì)偶映射，則對(duì)任意x、y∈E，有

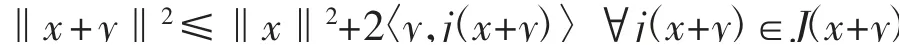
引理4[10]設(shè){an}和{bn}為2個(gè)非負(fù)實(shí)數(shù)列，滿足an+1≤（1-tn）an+bn，n≥n0，其中n0是非負(fù)整數(shù)，tn∈則有

2 主要結(jié)果

定理1設(shè)E為實(shí)一致光滑可分的Banach空間，C是E的非空閉凸子集，Ti（i=1，2，…，s）：Ω×C→C是具有函數(shù)k：Ω→（0，1）的s個(gè)連續(xù)廣義Lipschitz隨機(jī)強(qiáng)偽壓縮算子，Ti（ω，·）的不動(dòng)點(diǎn)集記為F（Ti（ω，·）），是由式（1）定義的多步隨機(jī)迭代序列滿足條件則序列{xn}強(qiáng)收斂到Ti的隨機(jī)公共不動(dòng)點(diǎn).

證明因?yàn)門i（i=1，2，…，s）：Ω×C→C是具有函數(shù)k（ω）：Ω→（0，1）的連續(xù)隨機(jī)強(qiáng)偽壓縮算子，任意給定ω∈Ω，Ti（ω，·）：C→C是具有k（ω）∈（0，1）的強(qiáng)偽壓縮算子，由引理2知Ti（ω，·）：C→C有唯一不動(dòng)點(diǎn)，即存在唯一的xi*（ω）∈C，使得xi*（ω）=Ti（ω，xi*（ω））.又因此，對(duì)任意給定的ω∈Ω，存在唯一的由式（1），對(duì)每一ω∈Ω，有

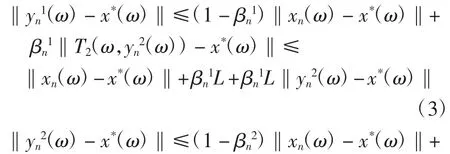
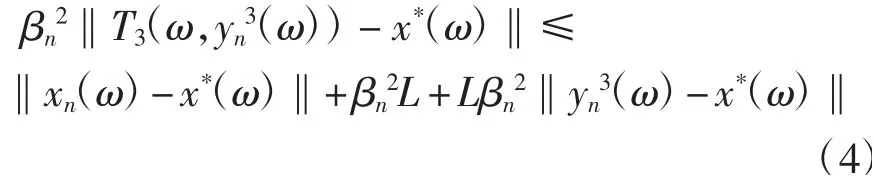
將式（4）代入式（3）可得

由式（1）連續(xù)做s-2步迭代，有

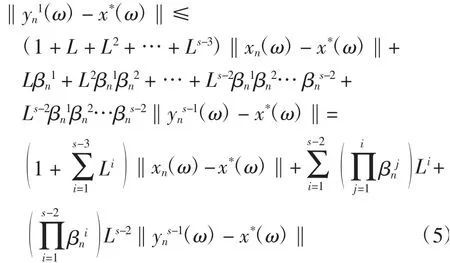
又由式（1）有

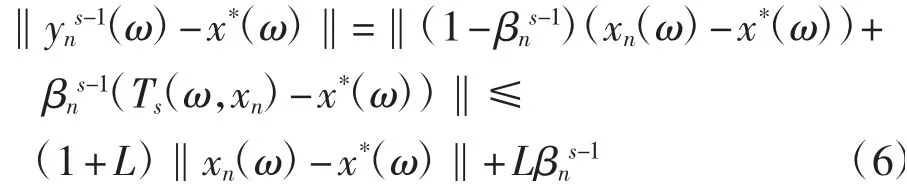
將式（6）代入式（5），可得對(duì)每一ω∈Ω，有

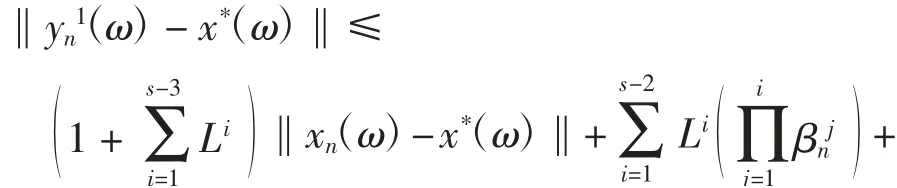
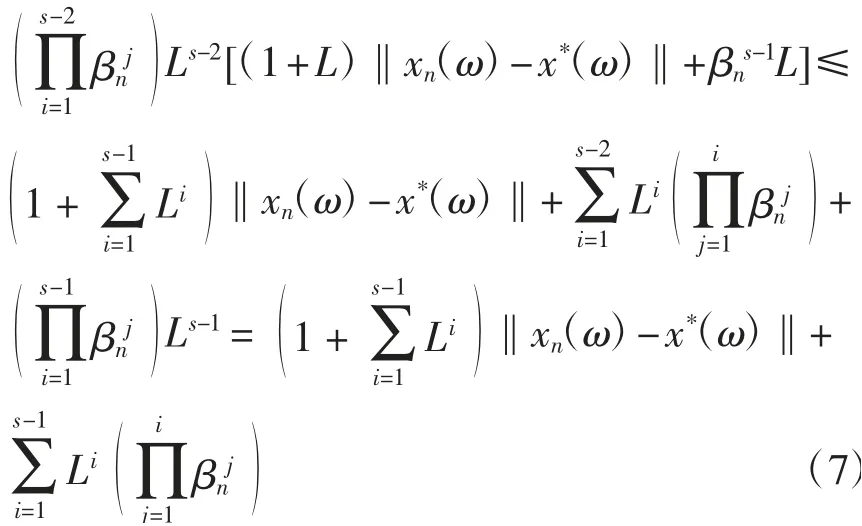
類似式（7）的證明過程可得

因?yàn)門i：Ω×C→C是廣義Lipschitz的，故存在常數(shù)L≥1，使得對(duì)任意x、y∈C及每一ω∈Ω，結(jié)合式（7）有

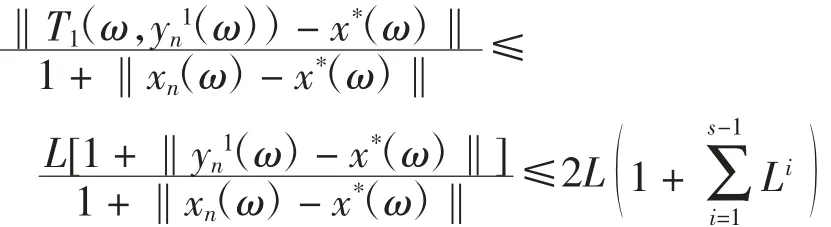
由式（1）和引理3，對(duì)每一ω∈Ω，有

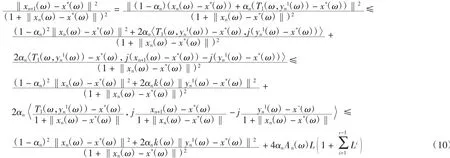
其中

下證An（ω）→0（n→+∞）.由式（1）和式（8），對(duì)每一ω∈Ω，有

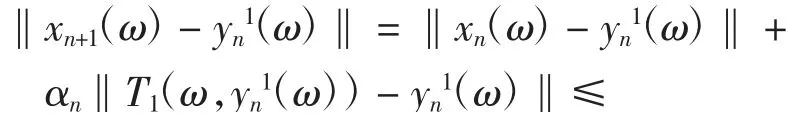
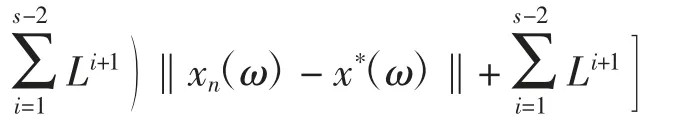
于是對(duì)每一ω∈Ω，有

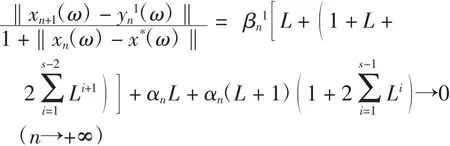
因?yàn)镋是一致光滑的Banach空間，故正規(guī)對(duì)偶映象J在E的任何有界子集上一致連續(xù)，于是由J的一致連續(xù)性可知：對(duì)每一ω∈Ω，有An（ω）→0（n→+∞）.

由式（1）和引理3以及式（8），對(duì)每一ω∈Ω，有

其中

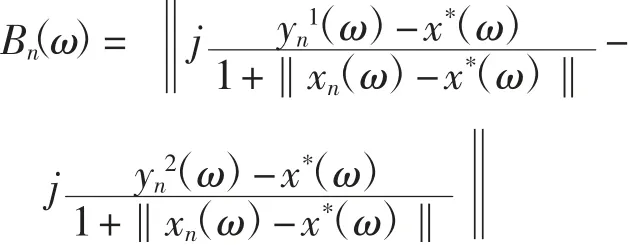
下證Bn（ω）→0（n→+∞）.由式（1），對(duì)每一ω∈Ω，有

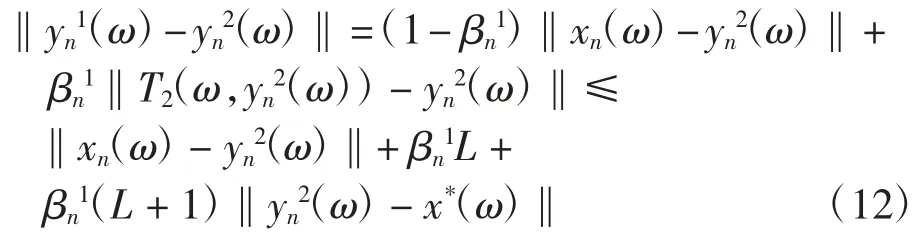
由式（1）和式（8），對(duì)每一ω∈Ω，有

將式（8）和式（13）代入式（12），有

由J的一致連續(xù)性知Bn（ω）→0（n→+∞）.

將式（11）代入式（10），對(duì)每一ω∈Ω，有

據(jù)此可得

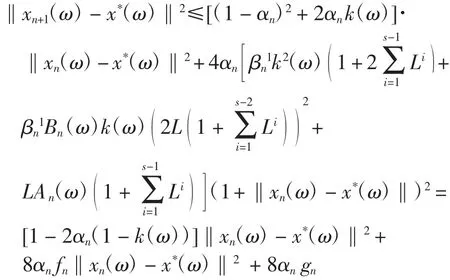
其中

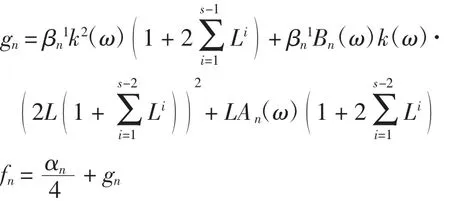
因?yàn)棣羘→0，gn→0（n→+∞），因此fn→0（n→+∞），于是存在正整數(shù)n0，對(duì)n>n0，有從而對(duì)任意n>n0，對(duì)每一ω∈Ω，有

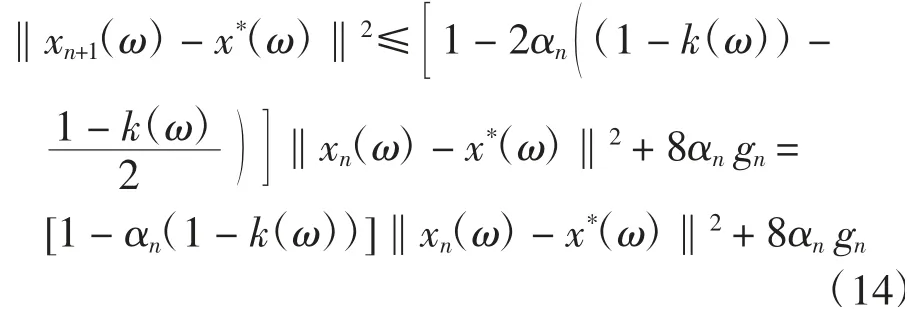
推論設(shè)E為實(shí)一致光滑可分的Banach空間，C是E的非空閉凸子集，T：Ω×C→C是具有函數(shù)k：Ω→（0，1）的連續(xù)廣義Lipschitz的隨機(jī)強(qiáng)偽壓縮算子.{xn（ω）}是由式（2）定義的隨機(jī)Ishikawa迭代序列.{αn}、{βn1}?[0，1]滿足條件則序列{xn}強(qiáng)收斂到T的隨機(jī)不動(dòng)點(diǎn).

作為上述結(jié)果的應(yīng)用，下面討論強(qiáng)增生隨機(jī)算子方程隨機(jī)解的迭代收斂性.

定理2設(shè)H為可分的Hilbert空間，T：Ω×H→H是具有函數(shù)h：Ω→（0，1）的連續(xù)隨機(jī)強(qiáng)增生算子.設(shè)f：Ω→H為一可測(cè)函數(shù)，令S：Ω×H→H為S=IT+f.x0：Ω→C為任意給定的可測(cè)函數(shù)，{xn（ω）}是由下式定義的隨機(jī)Ishikawa迭代序列，

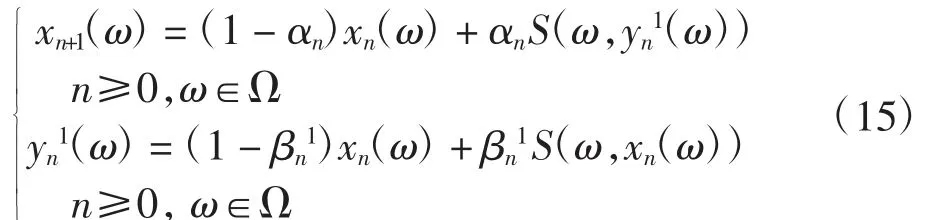
{αn}、{βn1}?[0，1]滿足條件（1）αn→0，βn1→0（n→+∞）；如果S是廣義Lipschitz的，則對(duì)任意給定的可測(cè)函數(shù)f：Ω→H，隨機(jī)算子方程

有唯一隨機(jī)解x*：Ω→H，且對(duì)每一ω∈Ω，隨機(jī)迭代序列{xn（ω）}強(qiáng)收斂到x*（ω）.

證明由條件可知S：Ω×H→H是具有函數(shù)k：Ω→H，k（ω）=1-h（ω）的連續(xù)廣義Lipschitz隨機(jī)強(qiáng)偽壓縮算子.由推論，對(duì)每一ω∈Ω，由式（15）定義的序列{xn（ω）}強(qiáng)收斂到S的隨機(jī)不動(dòng)點(diǎn)x*：Ω→H，因此S（ω，x*（ω））=x*（ω），即T（ω，x*（ω））=f（ω），ω∈Ω，這蘊(yùn)含x*（ω）是隨機(jī)方程（16）的隨機(jī)解.證畢.

注4本文從兩方面推廣和改進(jìn)了文獻(xiàn)[3]中的結(jié)果：（1）將隨機(jī)Ishikawa迭代序列推廣到多步隨機(jī)迭代序列；（2）用廣義Lipschitz算子取代值域有界條件.

例設(shè)Ω=[0，1]，取C=（-∞，+∞）具有通常意義的范數(shù).∑是Ω的σ-代數(shù)在[0，1]上的Lebesgue可測(cè)子集，定義隨機(jī)算子T：Ω×C→C為T（ω，x）=2ω-x，則對(duì)每一ω∈Ω，可測(cè)映象x*：Ω→C，x*（ω）=ω是T的唯一隨機(jī)不動(dòng)點(diǎn).對(duì)任意x、y∈C，存在j（x-y）∈J（x-y），使得對(duì)每一ω∈Ω，取有

由此T：Ω×C→C是一個(gè)具有的強(qiáng)偽壓縮算子，且是具有L=1的廣義Lipschitz算子.取則推論中的所有條件均滿足.因此由式（2）定義的序列{xn}強(qiáng)收斂到T的隨機(jī)不動(dòng)點(diǎn)x*（ω）=ω.事實(shí)上

但因?yàn)門的值域無界，因此文獻(xiàn)[3]中的定理2.1不能用于此算例.