基于概念設計的框架車身多目標優化系統

袁煥泉 李永成 陳東 耿富榮 趙永宏

摘要： 為實現概念設計階段車身結構和性能的快速優化，構建多工況、多目標優化系統FVO，其中包括車身幾何建模、有限元分析、結構優化等。該系統可以快速建立參數化框架車身幾何模型，自動生成滿足多工況要求的高精度有限元模型，利用多目標優化算法對車身的梁和板結構進行多工況優化計算，為用戶提供滿足眾多約束條件的優化設計方案。在闡述FVO系統整體結構和具體方法的基礎上，通過簡單設計實例證明系統的有效性和準確性。

關鍵詞： 正向設計; 優化設計; 多目標優化; 多工況; 車身概念設計

中圖分類號： TP391.92; U463.321 ? 文獻標志碼： B

Abstract： In order to realize the rapid optimization of the vehicle body structure and performance in the conceptual design， the system named FVO with multiple modes and multi-objective optimization is constructed， including geometric modeling， finite element analysis， structural optimization and other body design. By using this system， the parametric frame body geometric model can be established quickly， and the high precision finite element model in multiple modes can be generated automatically. The multi-objective optimization algorithm can be used to optimize the beam and plate of the vehicle body under multiple modes. The system provides users with an optimized design solution satisfying many constraint conditions. Based on the explanation of overall structure and specific methods of the FVO system， the effectiveness and accuracy of the system can be proved with simple design examples.

Key words： forward design; optimization design; multi-objective optimization; multiple modes; body concept design

0 引 言

經過多年的學習借鑒和技術積累，中國汽車行業的各大自主品牌已度過簡單模仿制造的階段，開始重視并加大汽車產品正向設計過程的投入，建立自己的生產平臺和產品體系。車身是汽車四大總成之一，其質量和生產成本都在整車中占較大比重，是正向設計中的關鍵部件。[1]車身結構的正向設計過程分為概念設計和詳細設計2個階段。[2]雖然在概念設計階段不能直接得到最終用于生產制造的車身尺寸數據，但是可以從整體上確定車身材料的分布形式，在很大程度上決定車身的結構性能和生產成本。[3]概念設計階段的小錯誤有可能導致詳細設計階段的大錯誤，從而造成整體設計返工事故。[4]

為更好地完成正向設計中的概念設計，直接進行生產制造的汽車企業除掌握必要的仿真技術外，還應注意：結構分析應考慮盡可能多的工況，以滿足產品實際使用要求;將設計方法系統化并形成相應的軟件工具，降低操作門檻，避免設計人員變動影響研發進度;應掌握軟件工具核心算法的源代碼，便于不斷完善軟件或用于其他研究。本文針對車身結構設計中的實際問題，深入研究并逐步解決概念設計階段的建模、分析和優化等問題，最終設計一套比較完善的多工況車身性能快速優化系統FVO。

SFE CONCEPT是目前市場上成熟的概念設計隱式參數化建模軟件[5]，該軟件需要基于參考車身的CAD或CAE模型進行參數化建模，在概念設計前期沒有完整數據的條件下很難進行車身結構性能優化。FVO基于框架車身進行概念設計，初期不需要參考數據支撐，比SFE CONCEPT建模更快。

現有的多目標優化商業軟件有Isight、OptiStruct等。與OptiStruct優化結果相比，FVO得到的優化數據更加理想，可以用于指導車身詳細設計。OptiStruct結構優化相對封閉，FVO具有良好的開放性，可以針對多個有限元模型展開優化，也可以調用第三方軟件（如LS-DYNA）進行求解計算，因此能更好地滿足實際需求，極大地簡化優化操作過程。

1 FVO系統特點

為降低開發和使用難度，選擇汽車行業常用的前處理軟件HyperMesh進行二次開發[6]，設計獨立的系統歡迎界面調用HyperMesh，即可進入內嵌有FVO系統的圖形界面。用戶不需要花費過多的時間學習，只需按照左側流程樹由上至下順序操作，或者根據實際需要選擇任意模塊進行操作。

為滿足企業研發生產的實際需求，FVO結構分析和優化可考慮的工況包括彎曲、扭轉和碰撞等。同時，作為多目標優化工具，FVO的目標函數既可以定義為車身結構各性能指標，也可以定義為車身質量，還可以同時定義為各參數的加權和。

優化求解器是FVO系統的核心部分，因此通過自編程序實現。目前，程序中集成的優化方法為移動漸近線法（method of moving asymptotes， MMA），該方法是一種穩定且快速的梯度優化方法。[7]自編程序雖然耗費更多的時間和精力，但可以允許研究人員對優化方法進行修改和完善，便于應用于后續的產品開發項目中。

FVO多目標優化系統具有以下顯著特點：（1）基于HyperMesh定制流程化工作環境，將系統功能分解為不同模塊，可降低學習和操作難度;（2）針對企業實際研發需求，擁有多個實用功能，并可考慮多種常用分析工況;（3）自主開發核心優化算法模塊，便于修改和應用于其他項目。

2 FVO系統結構和功能

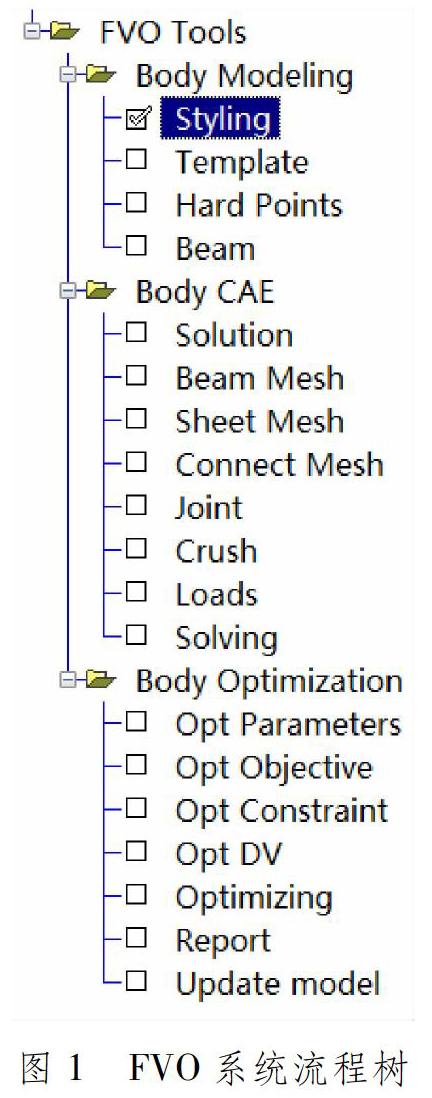
FVO系統針對實際需求設計流程化結構，思路清晰、便于操作，可以提高建模效率，其流程管理按照流程樹格式設計。FVO系統流程樹見圖2，其中參數化建模模塊Body Modeling、有限元分析模塊Body CAE和參數優化模塊Body Optimization為3個主要分支模塊，每個分支模塊包括若干并列的具體功能。使用Process Studio工具將各個模塊的具體功能集成到HyperMesh圖形界面的流程樹內，用戶只需按照流程樹的順序和頁面提示進行操作，即可完成整個優化設計過程。

2.1 參數化幾何建模模塊

在概念設計階段，車身模型不需要復雜的詳細結構，為減少建模和分析時間，在滿足精度要求前提下，可以采用能夠反映車身整體結構性能的簡化模型進行研究。[8]

在FVO系統中，車身幾何模型的梁結構采用直線段近似，曲率變化較大的梁結構采用多個直線段近似，板結構采用平面近似。同時，為縮短建模時間，采用模板技術對企業多種車型制作車身結構模板，某SUV車型模板見圖2。在實際建模過程中，導入相應車型的模板并進行尺寸修改即可。HyperMesh的幾何建模功能較弱，沒有參數化修改幾何模型的功能，因此采用自編程序修改幾何車身模板，實現參數化建模。改變車身結構關鍵部位的硬點坐標，與之相關聯的點、線、面都將發生位置和形狀變化。系統還允許通過增、減梁修改原結構的拓撲關系。

2.2 多工況有限元分析模塊

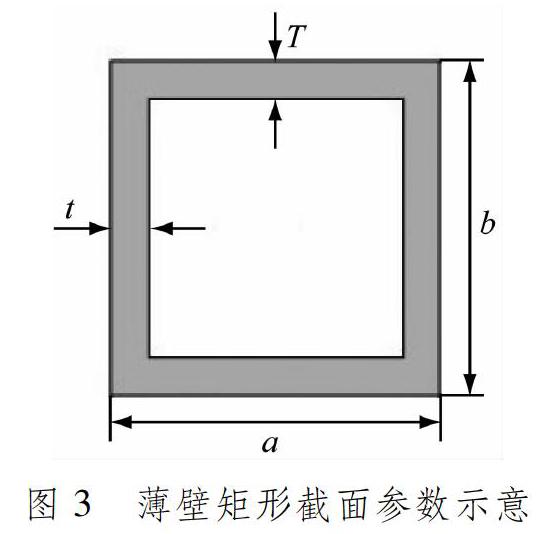
HyperMesh具有強大的前處理能力，FVO系統調用其成熟的有限元建模功能快速生成線性分析和碰撞分析2種車身模型。概念車身的有限元模型主要由一維梁單元和二維殼單元構成，梁單元截面可簡化為薄壁矩形結構。[9]薄壁矩形截面參數示意見圖3，a和b為長度尺寸，T和t為厚度尺寸。采用簡化模型不能得到直接用于生產的詳細梁截面參數，但可以計算得到截面面積、扭轉常數等參數。根據截面屬性指導截面設計，可滿足概念設計階段的需要。

為提高簡化模型的精度，對于同一平臺不同車型的通用部件或結構，FVO系統提供導入局部詳細模型的功能，例如可導入車輪罩的詳細有限元模型。但是，導入詳細結構模型將增加有限元分析的計算量和時間消耗，因此需要根據實際情況權衡模型精度與計算效率。

與線性分析有限元模型相比，碰撞模型復雜得多，因為碰撞分析涉及許多高度非線性分析過程，用簡化模型仿真比較困難。[10]在FVO系統中，碰撞模型的梁單元材料選用LS-DYNA中的MAT29并采用塑性鉸處理，即在MAT29材料中加入塑性鉸曲線定義，塑性鉸曲線可由公式計算得到。碰撞模型的殼單元材料選用LS-DYNA中的MAT24。簡化模型的各性能指標曲線與詳細碰撞模型的分析結果基本吻合。

FVO系統生成的某SUV車型有限元模型見圖4，對其進行一次提交計算，利用FVO系統內集成的計算公式計算得到彎曲剛度、前縱梁截面峰值力等性能指標，將該指標作為初始設計的響應值供優化模塊調用。

2.3 多目標結構參數優化模塊

HyperWorks內部集成OptiStruct優化求解器且調用方便，但其限制條件太多，且不能對LS-DYNA的碰撞模型進行計算和優化。因此，為實現多工況下的車身結構協同優化，FVO系統集成采用Tcl/Tk和C語言編寫的MMA，并應用于車身性能的多目標優化。自編優化程序有利于算法升級或用于其他研究項目，而不依賴于第三方軟件。

MMA為基于Fleury和Braibant的凸近似線性方法，是基于一階Taylor展開式的凸近似方法，其近似函數用原函數在當前設計點處的一階導數表示。[10]MMA通過引入移動漸近線，將隱式的優化問題轉化成一系列顯式可分離的嚴格凸近似子優化問題。在每一步迭代中，采用梯度類算法求解凸近似子問題，用于更新設計變量。與其他基于梯度信息的數學規劃方法相比，MMA具有穩定且快速的優點，可以節省大量的迭代計算時間，適用于對計算效率要求較高的工程實踐中。此外，為克服梯度算法只能找到臨近局部最優解這一缺點，SVANBERG[12]在原MMA的基礎上提出全局收斂型移動漸近線法（globally convergent version of MMA， GCMMA），通過內、外層迭代計算找到問題的全局最優解。在FVO系統中集成GCMMA，可使優化搜索過程具有全局性，從而找到更優解和更優設計方案。

目前，優化領域針對單目標優化的研究較為成熟，并且有大量的高效算法被提出;多目標優化的研究進展相對緩慢，優化算法的數量極少且計算效率一般不盡如人意[8]。單目標優化問題易于求解，但實際工程問題的優化方向往往不單一，而是在多目標之間相互權衡進行決策。FVO支持在Opt Objective頁面選擇任意性能指標或車身質量作為目標函數，并分配相應的權重[13]，即f=ni=1wifi

（1）式中：f為轉化后的目標函數;n為轉化前目標函數的數量;fi為轉化前第i個目標函數;wi為第i個目標函數對應的權重。

采用這一方法可以方便地將多目標優化問題轉化為單目標優化問題，不需要像多目標優化那樣花費大量時間求解Pareto前沿，從而簡化計算并節省時間。[14] FVO系統優化流程見圖5。

現有的優化方法需要進行反復迭代求解，車身結構優化問題需要進行大量的有限元分析，將耗費大量的研發時間。為此，FVO系統提供并行計算功能，即在更新設計變量過程中可同時進行多個有限元分析，從而極大縮短計算時間。用戶可以在Opt Parameters頁面定義并行計算的數目，但是并行計算會耗費大量計算資源，因此需要根據實際的計算機配置情況確定并行計算數目。

3 設計實例

以圖2的SUV車型開發為例，驗證FVO系統的優化結果。由于使用簡化模型，每一次的有限元分析只需30 s左右，遠遠低于詳細模型的分析時間。在相同優化參數設置下，與OptiStruct優化求解進行對比。優化問題的目標函數為車身質量，約束條件為車身彎曲剛度和扭轉剛度均不小于設定值，設計變量為車身結構中所有梁的4個截面尺寸（共144個，設計變量的取值范圍為初始值上、下浮動20%），收斂精度設置為0.001，最大迭代次數設置為20，并行計算數目設置為10。初始性能指標和2個優化系統的優化結果對比見表1。

由表1可知，優化后兩者的車身質量基本一致（相差不到2‰），扭轉剛度和彎曲剛度均滿足約束條件，說明FVO系統的優化效果較好。

FVO系統車身質量目標函數的迭代曲線見圖6。經過8次迭代優化后車身質量由289.12 kg降至232.11 kg，且第4次迭代后目標函數值已非常接近最終優化結果，迭代曲線非常理想。實際計算發現，適當提高收斂精度并經過更多次迭代后，FVO系統可以得到比OptiStruct更好的優化結果。

約束條件相同的車身彎曲剛度和扭轉剛度迭代曲線見圖7。經過第5次迭代后兩者均快速達到收斂，并且沒有違反約束，迭代曲線也非常理想。由此可見，FVO系統的優化結果是有效的。

4 結束語

為在概念設計階段實現車身結構和性能的快速優化，構建多工況、多目標優化系統FVO。該系統可以快速生成車身結構幾何模型，并基于HyperMesh二次開發生成高精度的線性分析模型和碰撞模型，集成MMA進行多工況、多目標的結構優化。某SUV車型簡化模型彎曲和扭轉混合工況下的輕量化設計實例證明該系統的有效性和準確性。

參考文獻：

[1] 黃天澤， 黃金陵. 汽車車身結構與設計[M]. 北京： 機械工業出版社， 2006.

[2] 侯文彬， 胡平， 劉大有， 等. 基于知識的車身結構概念設計工具——IVCD[J]. 吉林大學學報（工學版）， 2006， 36（5）： 814-818.

[3] 蘭風崇， 陳吉清， 林建國. 轎車參數化設計模型的構造和應用研究[J]. 計算機集成制造系統， 2005， 11（2）： 183-188.

[4] 莊蔚敏， 蘭鳳崇， 于多年， 等. 轎車參數化分析模型的構造及在車身開發中的應用研究[J]. 機械工程學報， 2004， 40（7）： 145-149. DOI： 10.3321/j.issn：0577-6686.2004.07.030.

[5] 瞿曉彬， 戴軼. 基于隱式參數化的白車身建模方法[J]. 計算機輔助工程， 2012， 21（2）： 42-45. DOI： 10.3969/j.issn.1006-0871.2012.02.010.

[6] 丁濤， 彭旺， 紀緒北. HyperMesh二次開發在客車CAE分析前處理上的應用[J]. 客車技術與研究， 2015， 37（6）： 47-49.

[7] SVANBERG K. Method of moving asymptotes： A new method for structural optimization[J]. International Journal for Numerical Methods in Engineering， 1987， 24（2）： 359-373. DOI： 10.1002/nme.1620240207.

[8] 徐濤， 左文杰， 徐天爽， 等. 概念車身框架結構的多變量截面參數優化[J]. 汽車工程， 2010， 32（5）： 394-398. DOI： 10.19562/j.chinasae.qcgc.2010.05.006.

[9] YIM H J， LEE S B， PYUN S D. A study on optimum design for thin-walled beam structures of vehicles[C]// Proceedings of International Body Engineering Conference and Exhibition. Paris： SAE， 2002.

[10] 肖海濤， 董江濤， 王月， 等. 某車型側面柱碰車身結構耐撞性優化[J]. 汽車安全與節能學報， 2015， 6（2）： 156-163. DOI： 10.3969/j.issn.1674-8484.2015.02.008.

[11] 王海軍. 解非線性最優化問題的移動漸近線法及應用[D]. 南京： 南京航空航天大學， 2010. DOI： 10.7666/d.d167257.

[12] SVANBERG K. A class of globally convergent optimization methods based on conservative convex separable approximations[J]. SIAM Journal on Optimization， 2002， 12（2）： 555-573. DOI： 10.1137/S1052623499362822.

[13] 蘇瑞意， 桂良進， 吳章斌， 等. 大客車車身骨架多學科協同優化設計[J]. 機械工程學報， 2010， 46（18）： 128-133. DOI： 10.3901/JME.2010.18.128.

[14] 龍騰， 劉莉. 改進的Pareto多目標協同優化策略[J]. 系統工程與電子技術， 2012， 34（9）： 1834-1840. DOI： 10.3969/j.issn.1001-506X.2012.09.15.

（編輯 章夢）