借助幾何畫板，對2017年全國2卷20題的思考

雒曉雅 吳帝春

[摘? 要] 文章以2017年全國2卷第20題第（2）問為載體，以幾何畫板為探究工具，展現(xiàn)了思考此題的思維過程，旨在從幾何角度尋求該定點的位置，在探究過程中意外找到了高等幾何背景下極點極線的“配極原則”與此題的聯(lián)系.

[關(guān)鍵詞] 幾何角度;極點極線;配極原則

圓錐曲線中極點極線的定義

已知圓錐曲線C：Ax2+Cy2+2Dx+2Ey+F=0（A2+C2≠0），則稱點P（x0，y0）和直線l：Ax0x+Cy0y+D（x0+x）+E（y0+y）+F=0是圓錐曲線C的一對極點極線.

引例：（2017年全國2卷（理），20題）設(shè)O為坐標原點，動點M在橢圓C：■+y2=1上，過M作x軸的垂線，垂足為N，點P滿足■=■■.

（1）求點P的軌跡方程;

（2）設(shè)點Q在直線x=-3上，且■·■=1，證明：過點P且垂直于OQ的直線l過C的左焦點F.

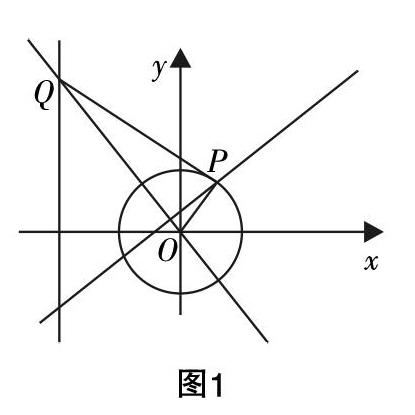
由（1）知，點P在圓x2+y2=2上運動，而點Q在直線x=-3上，即已知點Q的橫坐標為-3，且滿足■·■=1，則一個點P決定一個點Q的位置，即決定點Q的縱坐標，由此決定了垂線l的位置. 觀察幾何畫板動態(tài)的過程，隨著點P的運動，點Q隨之運動，直線l隨之運動，但在運動過程中，動直線l恒過一定點. 通過這樣的分析，可知，決定定點位置的要素有：圓、直線x=-3及向量數(shù)量積■·■=1，因此，如果改變這些值的大小，盡管會改變點的位置，但很可能不會改變直線l恒過定點的事實. 本文懷揣著這樣的猜想，旨在探尋該定點的幾何意義.

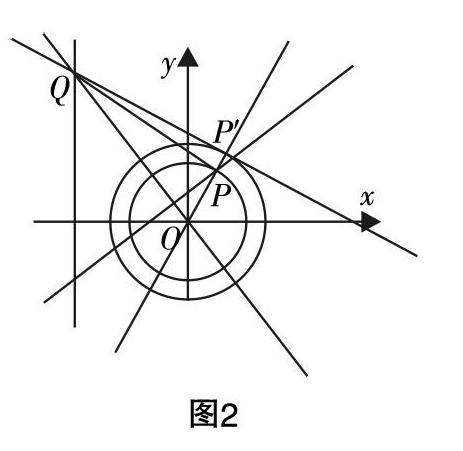
首先，若要從幾何角度考慮，需要考察數(shù)量積■·■=1的幾何意義，在點P運動過程中，■為定值■，因此“點Q滿足■·■=1”可以等價表述為“點Q滿足■在■方向上的投影為■”，因此，過點Q作直線OP的垂線，設(shè)垂足為P′，滿足OP′=■OP，在這里，改變■·■的值，將影響點P′的位置，（例如，當■·■=-1時，P′在直線OP上，且滿足■=■■;當■·■=0時，P′和點P重合），無論數(shù)量積為何值，點P′的軌跡為圓，圓心O2為（O2與O重合），于是點Q為“圓O2在點P′處的切線與直線x=-3的交點”.

要尋找?guī)缀我饬x，就得脫離直角坐標系，來觀察這個動態(tài)過程，不妨繞過點P，從P′點出發(fā)，有如圖3所示的幾何問題：

點P′為圓O上任意一點，過點P′作圓O的切線，交定直線m于點Q，過點P′作直線OQ的垂線，記作l，證明：直線l恒過一定點.

顯然，對于定圓來說，直線m的位置影響著該定點的位置，于是筆者開始探索直線m的位置與待求定點的關(guān)系.

不妨先按照特殊情況來研究，當定直線m與圓O相切時，如圖4所示，顯然能夠得出動直線l恒過定點，該定點為定直線m與圓O的切點.

而借助幾何畫板，發(fā)現(xiàn)當定直線m與圓O相交時，待求定點在圓外;當定直線m與圓O相離時，待求定點在圓內(nèi)，這不禁讓人聯(lián)想到極點極線的配極原則.于是大膽猜想，待求的定點即為直線m在圓O上所對應(yīng)的極點.

證明：如圖4，5，6所示，設(shè)直線m所對應(yīng)的極點為M，只需證明在三種情形下，均有P′M⊥OQ即可.

此時筆者發(fā)現(xiàn)自己繞了很大的一個圈子，無論直線m與圓O的位置關(guān)系如何，題意中“過點P′作直線OQ的垂線”，即意味著過點P′作點Q對圓O的極線，根據(jù)配極原則，若點Q恒在直線m上，則點Q所對應(yīng)的極線恒過定點，記為M′，并且該定點M′即為直線m所對應(yīng)的極點.

結(jié)論：綜合以上分析，數(shù)量積■·■影響著圓O2的半徑，或者說點P′的位置;待求定點M′即為直線m在圓O2上所對應(yīng)的極點.

利用這道題目的數(shù)據(jù)來解釋以上原理，由于■·■=1，可構(gòu)造圓心在原點O，半徑為■的圓，作圓O在點P′處的切線與直線x=-3的交點，記為點Q. 根據(jù)極點極線的定義，“過點P′作OQ的垂線”即為“過點P′作點Q所對應(yīng)的極線”. 由于點Q恒在直線x=-3上，則它所對應(yīng)的極線恒過定點，而題意中要求的是“過點P作OQ的垂線”，即“過點P作點Q所對應(yīng)極線的平行線. 由于極線恒過定點，那么它的平行線也恒過另一個定點.”

接下來考慮兩個定點之間的位置關(guān)系：

我們來考慮下面幾何模型：當直線l1恒過定點1（M′）時，當點P′（或點P）繞著圓心運動，l1的平行線l2必然恒過定點M，且滿足定點1（M′）、定點2（M）及圓心三點共線，并有比例關(guān)系■=■.

現(xiàn)在根據(jù)上面的分析，來敘述一下本題中第（2）問定點（-1，0）的產(chǎn)生過程：在此題中，點P為圓x2+y2=2上任一點，由于滿足■·■=1，導致垂足點P′在圓x2+y2=■上運動，而直線x=-3關(guān)于圓x2+y2=■的極點為-■，0，即為定點1（M′）. 由于■=■，可推出定點2（M）坐標為（-1，0）.

通過以上分析，了解了題意中各個條件之間的關(guān)系，筆者有了以下幾道改編題供大家思考：

（1）設(shè)點Q在直線x=-1上，且■·■=0，證明：過點P且垂直于OQ的直線l恒過定點.

（2）設(shè)橢圓C的左焦點為F，過原點O作直線PF的垂線l，作點P處的切線交直線l于點Q，問：是否存在定直線，使得點Q在該直線上，若存在，請求出直線方程;若不存在，請說明理由.

（3）設(shè)橢圓C的左焦點為F，過原點O作直線PF的垂線l，點Q在垂線l上，且滿足■·■=1，證明：點Q恒在直線x=-3上.