例談尋找解題切入點的策略

王鳳君

[摘? 要] 解題是數(shù)學學習中的一項重要活動，解題能力的提升離不開有效的解題訓練，自然更少不了一些必要的解題策略. 教師需從以下幾個方面著手，引導學生找尋解題切入點，發(fā)展解題能力：挖掘隱含條件，剖析結(jié)構(gòu)特征，運用特殊化策略，采用數(shù)形結(jié)合以及利用差異分析法.

[關(guān)鍵詞] 解題;隱含條件;解題路徑;切入點;差異分析

數(shù)學的學習離不開對解題的探索，如何通過必要訓練去提高解題能力，應是廣大數(shù)學教師和學生不斷思考與探索的課題. 筆者在平常的教學中發(fā)現(xiàn)，不少學生在解題的時候存在以下問題：有些題目似曾相識，即使冥思苦想?yún)s依然找尋不到解題入口，當別人稍加提點卻又豁然開朗. 事實上，“老虎吃天，無處下爪”是學生在解題中的常見現(xiàn)象，究其根本在于學生尚未找尋到解決問題的突破口，當適當點撥時又會恍然大悟.所以，解題教學中需強化、引導學生去選擇一個容易攻克的切入點，由點及面，讓問題的本質(zhì)逐步自然展現(xiàn). 那么，如何找尋解題的切入點呢？下面筆者通過對多個案例的探究，談談具體的解決策略.

隱含條件：獲得解題路徑的關(guān)鍵

隱含條件，望文生義就是隱藏在數(shù)學問題中的一些含而不露的條件，它可以隱于圖形之中，也可藏于概念之中，還可匿于已知條件的相互聯(lián)系之中. 因此，在解題中學生需善于將這些隱含于題目中的“金針”挖掘出來，從而獲得解題的關(guān)鍵性突破，使問題迎刃而解.

例1：已知直線m被兩條平行線l1：x-y+1=0和l2：x-y+3=0所截線段長度為2■，那么直線m的傾斜角可能是①15°;②30°;③45°;④60°;⑤75°. 以上符合要求的序號有________. （請寫出所有正確答案的序號）

分析：通過觀察，不難得出本題中已知條件有①l1，l2為兩條平行直線;②直線m被l1，l2所截線段長度為2■. 而以上兩個條件對于問題中需求直線m的傾斜角是遠遠不夠的，那么下一步自然就需要深入題目挖掘隱含條件. 首先，據(jù)條件“l(fā)1，l2為兩條平行直線”，可以探求出兩直線間的距離為■;接著，再次觀察不難發(fā)現(xiàn)：直線m被l1，l2所截線段長度為l1，l2之間距離的兩倍;然后，借助作草圖可以發(fā)現(xiàn)，直線m與直線l1的夾角為30°，而直線l1的傾斜角為45°，則可很快得出直線m的傾斜角為30°+45°=75°或45°-30°=15°，故本題答案為①⑤.

設計說明：讓學生通過計算l1，l2之間的距離，并結(jié)合線m被l1，l2所截線段長度為2■，感知隱含條件的挖掘過程，得出隱含條件“直線m與直線l1的夾角為30°”，突破思維的難點，從而快速求解.

結(jié)構(gòu)特征：構(gòu)成解題路徑的基石

一般數(shù)學題都具有明顯的結(jié)構(gòu)特征，而其中的結(jié)構(gòu)特征往往直指解決問題的切入口. 這就需要在解題過程中，仔細觀察題目的外部特征，深入分析題目的深層結(jié)構(gòu)，在剖析問題的結(jié)構(gòu)特征中抓住問題的切入點，實現(xiàn)條件向結(jié)論的轉(zhuǎn)化.

例2：已知f（x）=■，試求出f（1）+f（2）+f■+f（3）+f■+f（4）+f■的值.

分析：本題可以首先計算f（1），f（2），f■，f（3），f■，f（4），f■的值，然后再求出f（1）+f（2）+f■+f（3）+f■+f（4）+f■的值，然而過程的煩瑣是可想而知的. 此時，不妨去觀察式子f（1）+f（2）+f■+f（3）+f■+f（4）+f■的特征，很快可以發(fā)現(xiàn)f（2）和f■，f（3）和f■，f（4）和f■中每一對自變量乘積都等于1，遮擋規(guī)律的“外衣”被迅速剝離，從而自然想到考慮這三對函數(shù)值的特征. 不少學生可以思考到去計算f（2）+f■，從而引申到f（x）+f■，則有f（x）+f■=■+■=■+■=1，所以f（1）+f（2）+f■+f（3）+f■+f（4）+f■=■+1+1+1=■.

設計說明：學生在解題時，需將著眼點置于對題目目標結(jié)構(gòu)特征的分析和聯(lián)想上，有針對性地找尋解題的入口，從而快速找到解題的有效策略.

特殊化策略：獲得解題入口的捷徑

人們認識客觀事物的普遍規(guī)律就是從特殊到一般的思路. 因此，在探究一些一般性問題的時候，我們可以通過研究它的某些特殊情形，為問題的探求提供幫助，從而找尋到問題的解決入口. 而正是這種特殊化策略的靈活運用，才能將認識過程中以退為進的思想方法體現(xiàn)得淋漓盡致.

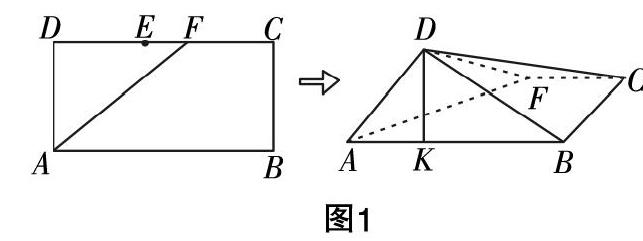
例3：如圖1，已知長方形ABCD中，有AB=2，BC=1，且E為DC的中點，動點F在線段EC上（不與E，C重合）. 現(xiàn)沿AF折起△AFD，使得平面ABD⊥平面ABC，在平面ABD內(nèi)過點D作DK⊥AB于K點.設AK=t，那么t的取值范圍為________.

分析：本題若以一般方法著手解決，過程煩瑣且難度較大. 若從特殊化策略入手，也就是從兩個極端位置進行思考，則可簡化解題過程. 當動點F移動到DC的中點時，可以得出t=1. 當動點F移動到C點時，有CB⊥AB，CB⊥DK，所以CB⊥平面ADB，即CB⊥BD. 因為CD=2，BC=1，所以BD=■. 又因為AD=1，AB=2，所以AD⊥BD，則t=■，由此可得t的取值范圍為■，1.

設計說明：本題通過引導學生思考動點F的兩個特殊位置“DC的中點和C點處”，從而快速找尋到解決本題的入口，給出特殊化策略解題的范例，讓學生感悟復雜問題和一般問題的解題方法.

數(shù)形結(jié)合：尋求解題入口的法寶之一

數(shù)形結(jié)合解題的重點是數(shù)與形的相互表征，實現(xiàn)數(shù)與形的相互轉(zhuǎn)化.在數(shù)形結(jié)合解題的過程中，找尋數(shù)與形的轉(zhuǎn)化途徑從而尋找解題突破口不僅是一個重點，也是一個難點. 因此，在解題教學中，教師可以通過富有探究性的題目，引領學生從問題本身進行探索性活動，在解決問題的過程中，將抽象的數(shù)學語言與直觀的圖形相溝通，實現(xiàn)抽象與具體的轉(zhuǎn)化和滲透，大跨度地遷移自身已有的思維方式，從而找尋到解決問題的突破口.

例4：已知函數(shù)f（x）=lgx，010.若a≠b≠c，且f（a）=f（b）=f（c），則abc的取值范圍為（? ）

A（5，6） B. （1，10）

C. （20，24）？搖？搖？搖？搖？搖？搖 D. （10，12）

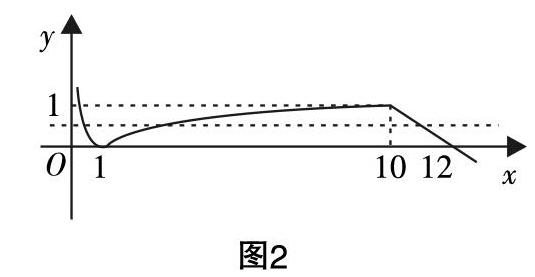
分析：易得函數(shù)f（x）為分段函數(shù)，可以通過作草圖來演繹圖像的變換，由此簡化解題過程. 觀察圖2可知，若要f（a）=f（b）=f（c），可以設a

設計說明：通過本題的典型性來凸顯數(shù)形結(jié)合思想方法的優(yōu)勢，讓學生在解決問題的過程中，培養(yǎng)學生思維的發(fā)散性和想象力，在解題完畢還可以進一步進行總結(jié)與提升，在回顧和概括中提升思想方法的應用能力.

差異分析法：尋求解題入口的又一利器

在解題中，我們會發(fā)現(xiàn)一些題目的條件與結(jié)論之間無論在形式或結(jié)構(gòu)上，還是在圖形或文字間都存在著一定的差異性，我們將它們之間的差異稱為“目標差”. 成功解題的關(guān)鍵就是從找尋目標差入手，通過一個方案的設計來不斷縮小這里的目標差，直到目標差消除，從而在找尋、分析、消除目標差的過程中快速形成解題方案，這種解決問題的方法就是差異分析法. 該方法可以幫助學生快速找尋到解題入口，成為解決復雜數(shù)學題的利器.

例5：已知tan2θ=-2■，■<θ<π，試求■.

分析：首先，從角的差異著手，目標中除θ以外，還有■和θ+■，分析題設，只能找尋到2θ這一個，而事實上它們都可以轉(zhuǎn)化為θ;其次，從三角函數(shù)名稱的差異著手，目標中僅有“弦”，而題設之中僅有“切”，事實上它們也可以相互轉(zhuǎn)化.從而，成功突破本題的關(guān)鍵在于縮小并消除角與三角函數(shù)名稱的目標差.

解：原式=■=■=■. ？搖據(jù)tan2θ=■= -2■，可解得tanθ=-■或tanθ=■. 因為■<θ<π，tanθ=-■，所以原式=■=3+2■.

設計說明：本題巧借差異分析法，從找出差異開始搭建解題通道，并不斷變換思維的視角，關(guān)注到角與三角函數(shù)名稱的目標差，快速聯(lián)結(jié)解題的思維路線，在消除目標差的過程中完善解題路徑.

總之，解題教學的價值并非在于解題的數(shù)量，而是需借助解題活動來提升學生解決問題的策略，這才是解題教學的價值取向. 因此，我們在精選例題訓練時，需站在學生的角度，精選具有典型性和價值性的例題，并以思維為主線，共同展示找尋解題突破口的全過程，讓學生在感受和體驗中落實每個例題固有的“生長”功能，從而實現(xiàn)解題教學的意義和價值. 只有持之以恒，才能真正意義上解決學生面對難題時“習得無助”的問題.