融合時空信息和興趣點重要性的POI推薦算法

李寒露，解 慶，唐伶俐，劉永堅

（武漢理工大學計算機科學與技術學院，武漢 430070）

0 引言

興趣點（Point-Of-Interest，POI）推薦一直受著基于位置的社 交 網 絡（Location-Based Social Networks，LBSNs）（例 如Foursquare和Facebook等）快速發展的推動。這些LSBNs允許用戶彼此連接，發布物理位置并分享與位置相關聯的信息［1］。而LBSNs 中的POI 推薦意在幫助用戶探索新的和有趣的地方。例如，當用戶去吃飯時，推薦系統會為用戶找到附近其感興趣的餐館或者小吃的詳細信息；這樣不僅可以改善用戶的體驗，同時也能為商家帶來新的目標客戶。目前，大多數研究主要在協同過濾（Collaborative Filtering，CF）的基礎上加入其他影響因子進行推薦，但是存在以下幾點不足：

1）數據噪聲過濾方法需要改進：龐大的用戶簽到數據中不可避免地混雜許多噪聲數據，過多的噪聲數據會導致推薦質量的降低［2］。如果能夠在數據預處理階段提前過濾掉不符合用戶行為習慣的簽到信息數據，可以提高推薦的精度，降低計算量。

2）興趣點重要性分析未能有效考慮用戶個性化因素：在LBSNs中，通常按照訪問次數排序的方法計算興趣點重要性，但僅僅考慮用戶的訪問次數，會導致興趣點重要性對于所有用戶都是同等的，而實際上，對于不同的用戶每個興趣點的重要性是不同的。

針對上述問題，本文提出了RecSI（Recommendation by Spatiotemporal information and POI Importance）模型，主要貢獻如下：

1）將地理信息和興趣點之間吸引力設置為預處理條件，過濾數據集中的數據噪聲。

2）引入用戶社交關系網絡，通過計算用戶與好友之間的相似程度和興趣點對于好友的重要程度，來評估興趣點對于目標用戶的重要性。

1 相關工作

協同過濾（CF）是興趣點推薦中最常見的技術，它分為基于記憶和基于模型的方法。基于記憶的方法又分為基于項目和用戶兩類。在基于用戶的方法中，通過采用諸如Cosine 或Pearson 的測量函數來計算某些用戶之間的相似性權重。隨后，將使用相同POI上的類似用戶的評級來計算用戶訪問POI的概率［3］。而在基于項目的方法中，首先找到共同訪問的POI，然后計算在類似POI 上的用戶評級的加權混合［4］。但是這些方法都未能取得很好的推薦結果，因此，不少研究加入其他的影響因子以改進推薦的結果。

地理影響［3-6］在POI 推薦中起著至關重要的作用，因為用戶在LBSNs中的活動受到地理位置的限制。Cheng等［5］假設用戶傾向于在幾個中心周圍進行簽到活動，并使用多中心高斯模型（Multi-center Gaussian Model，MGM）對同一用戶的兩個位置之間的距離進行建模，以捕獲地理影響，然后進一步用矩陣分解進行POI 推薦。Ye 等［3］通過采用冪律分布（Power-law Distribution，PD）對用戶的位置進行建模，并提出了一種基于地理影響的樸素貝葉斯POI 推薦算法。Zhang 等［6］認為，當LBSNs向用戶推薦POI而不是所有用戶的共同分布時，應該個性化對用戶移動性的地理影響，所以他們通過使用核密度估計（Kernel Density Estimation，KDE）來模擬地理影響。

在POI 推薦中，一般利用時間影響［7-12］來提高在特定時間向查詢用戶推薦新位置的概率。例如，人們總是在工作日和周末訪問不同的地方，用戶的偏好也會發生改變。Guo等［7］通過將用戶的簽到時間進行分段，并且對較近的時間段賦予較高的權重進行推薦。Zheng 等［8］利用時間戳將原始用戶POI信息進行劃分，結合LDA（Latent Dirichlet Allocation）算法［9］來推斷用戶的興趣和POI 的主題分布進行POI 推薦。大多數關于時間影響的研究都只是經驗性地對時間進行均勻劃分，沒有考慮用戶訪問POI 時間上的動態性，所以王楠等［11］在利用多種信息進行時間敏感的新位置POI 推薦，提出基于層次聚類的時間動態分段算法，結合直接朋友和潛在朋友兩種社交關系構建模型。

在LBSNs 中社交因素［13-17］也起著重要的作用。在日常生活中，人們在訪問新的地方時往往會詢問朋友的意見，因此利用用戶之間的社交關系在一定程度上能夠解決冷啟動問題，提高推薦的準確率。Li等［13］認為用戶的簽到空間由社交朋友空間和用戶的興趣空間兩部分組成，并分別構建了社交朋友概率分解（Social Friend Probabilistic Matrix Factorization，SFPMF）模型和用戶興趣概率分解（User Interest Probabilistic Matrix Factorization，UIPMF）模型，然后將兩種分解模型進行線性融合來進行興趣點推薦。Li等［16］認為LBSNs網絡中存在三種朋友，并開發了一個兩步框架來利用三種朋友信息來提高興趣點推薦的準確性。

2 問題分析

在本章中介紹一些與模型相關的方法和概念。在這之前先定義問題的描述。

2.1 問題描述

LBSNs 上面匯集了大量用戶的歷史簽到數據，這些歷史簽到數據中包含的各種上下文信息能夠為分析用戶偏好提供幫助，從而進一步提高興趣點推薦的精度。LBSNs 中包含了用戶集合U={u1，u2，…，un}、興趣點集合L={l1，l2，…，lm}，n、m分別是用戶和興趣點的數量。數據集D={d1，d2，…}，其中di={u，l，t}，由用戶u、興趣點l和簽到時間t組成，描述了用戶u在時間t訪問了興趣點l。

興趣點推薦 根據已有簽到數據d={u，lj，t}，向用戶u推薦在某個時刻t上他可能感興趣但還未訪問的前K個興趣點集合。

為了方便討論，表1列出了本文使用的一些重要符號。

表1 本文所用符號及其描述Tab.1 Symbols used in this paper and their descriptions

2.2 興趣點中的地理影響

一般情況下，人們外出活動的范圍經常受到地理位置的限制。在歷史簽到數據中，可以發現用戶的歷史簽到行為往往呈現出聚類的現象，并發生在相對較近的空間內，造成用戶簽到空間的空間聚類［3］，因此，在對目標用戶進行POI 推薦時，POI的地理位置起著至關重要的作用。POI的地理位置分為用戶與POI之間的距離和POI與POI之間的距離，根據經驗通常用戶更傾向于訪問距離較近的興趣點，并且所訪問的興趣點受到以前所訪問過的興趣點的影響，兩個興趣點之間的吸引力越大，相互間的影響力越大，用戶訪問的概率就越大。

文獻［2］驗證在Foursquare 數據集中，發現超過89.3%以上的用戶平均簽到的距離在10 km 以內，分析得出人們更傾向于訪問與之前的記錄相近的興趣點，并提出基于位置的過濾算法將原始數據根據距離信息進行過濾，以排除遠離日常活動范圍的興趣點。本文在此的基礎上加入興趣點之間的吸引力來進一步過濾候選集的范圍。

根據文獻［18］提出的式（1）計算所有用戶已訪問過兩個POI之間的相互影響力：

其中：gi表示POIli地理的地理影響力，hj表示POIlj相對POIli的地理敏感性，di，j表示兩個POI 之間的距離。根據文獻［19］知道POI 之間的距離符合冪律分布，因此根據冪律分布得到公式f(di，j)=，其中di，j表示兩個興趣點之間的距離。

式（1）的結果如圖1 所示，圖中橫坐標表示任意兩個POI之間的吸引力，縱坐標表示任意兩個POI 之間平均吸引力小于指定區間的用戶比例。

如圖1顯示，超過80%以上的POI之間存在超過0.6以上的相互吸引力，可以認為當POI 之間相互吸引力超過0.6 時，用戶訪問的概率越大。通過相互之間的吸引力的計算，可以分析得出人們在相同的距離下，更傾向于訪問POI 之間吸引力更大的興趣點。

因此本文提出基于興趣點之間吸引力的過濾算法（Attractiveness between POIs based Filtering Algorithm，APFA），將原始數據集分別基于距離和POI 之間相互吸引力進行過濾，去除用戶平時出行范圍內很少去的POI，與用戶已經訪問過的POI 相互之間吸引力較小的POI 進行過濾得到兩個候選集，最后將這兩個候選集合并取交集，形成最后的用于推薦的候選集，以避免噪聲POI的影響，提高推薦的精度。

圖1 興趣點之間相互吸引力Fig.1 Mutual attraction between POIs

3 RecSI模型

本章描述本文提出的POI 推薦模型RecSI。RecSI 模型由兩個部分組成：一個是用戶對于興趣點的偏好程度；另一個是興趣點對用戶的重要性。該模型的主要貢獻在于：1）考慮到一天中不同時間段內用戶對POI 類別的偏好程度不同，計算用戶在每個時間段內的偏好；2）將興趣點對用戶的重要性加入到最后的推薦模型中，提高了推薦的質量。

3.1 基于時間因素的用戶偏好建模

根據用戶在一天中不同的時間段內對興趣點的偏好程度不一樣，本文在文獻［11］提出的基于層次聚類的時間動態分段方法的基礎上討論用戶在每個時間段的用戶偏好，本文將時間段分為4段。

研究表明，用戶在一天中不同的時間段對興趣點的喜愛程度是不同的，而在LBSNs 中POI有不同的類別，每個類別信息都可以反映POI 提供的服務以及服務的風格，當一個用戶越喜歡某一個種類，在時間段t內訪問這個類別所屬的POI就越頻繁，因此可以通過分析在時間段內用戶所訪問的POI 的類別信息來挖掘用戶的偏好程度。

在本文的數據集Foursquare 中每個POI 都是由8 個類別和240個子類別標記，通過式（2）計算用戶u在時間段t內對所有POI類別的偏好得分向量，以此構建用戶u的類別偏好向量，用于表示用戶u在時間段t內對不同類別POI的偏好程度。

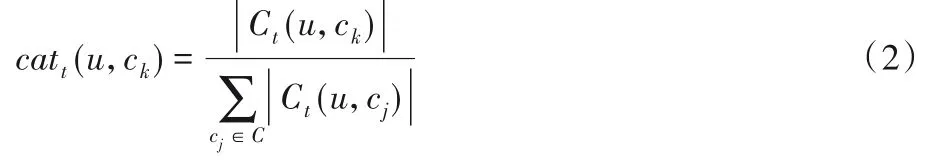
其中Ct(u，ck)表示用戶在時間段t內在ck類別的POI上的簽到總數。

但是類別偏好向量只是表示了用戶u對某一類POI 的偏好程度，而每個種類的POI 里面有包含很多的POI，將這里面的POI同等重要的推薦給用戶是不合理的。實際上，每個POI對于用戶而言都有不同的吸引程度，同類別中越受歡迎的POI 對用戶的吸引力越大，用戶簽到就越頻繁，因此為了捕獲同類別中POI 的受歡迎程度，引入POI 的受歡迎程度（即POI的流行度）作為同類別不同POI的權重。

根據用戶的歷史簽到數據，可以得到兩個數據標簽：POI在時間段t內總訪問的用戶量Ucountt(lj)和POI的總簽到數量Pcountt(lj)，這兩個數據標簽可以很直觀地表現出POI 的受歡迎程度，在對其進行標準化后，根據式（3）計算兩者之間的幾何平均數，得到在時間段t內POIlj的流行度：

由此本文在考慮類別信息和流行度的同時，根據式（4）計算用戶u在時間段t內對POI的偏好：

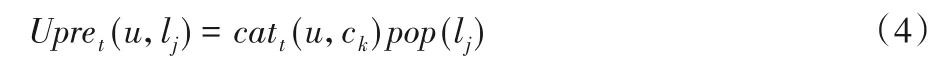
3.2 基于興趣點重要性建模

興趣點的重要性在一定程度上會影響推薦結果。以前的研究多數是按照訪問次數排序的方法計算興趣點重要性，僅僅考慮用戶的訪問次數，從而導致興趣點重要性對于所有用戶都是同等的，但實際上，對于不同用戶而言每個興趣點的重要程度是不同的。因此本文將引入用戶社交關系網絡，通過計算用戶與好友之間的相似程度和興趣點對于好友的重要程度，來計算興趣點對于目標用戶的重要程度。具體按照下面的順序計算興趣點對用戶的重要性：

1）計算用戶與好友之間的相似程度。

根據用戶在LBSNs 中的簽到信息和社交關系，將用戶的朋友定義為位置好友和社交好友兩種，具體定義如下：

其中α表示相似因子，siml(u，v)和sims(u，v)分別表示好友位置相似性和好友相似性，由式（7）、（8）計算得出：

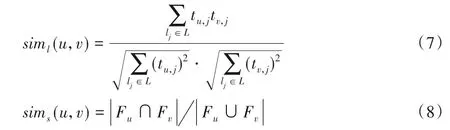
其中tu，j表示用戶u在興趣點lj的訪問狀態：若tu，j=1，代表用戶u在興趣點lj進行了簽到；tu，j=0 則 代表用戶u未進行簽到。Fu與Fv分別代表用戶u與用戶v的好友集合。

2）計算用戶好友中每個興趣點的重要程度。

本文定義了一個興趣點上下文圖來捕獲興趣點對用戶的重要程度。

定義3興趣點上下文圖。興趣點上下文圖表示為GLL=(L，ELL)，其中頂點lj∈L表示用戶所訪問過的興趣點，有向邊e=(li，lj)表示用戶在某一天中訪問了興趣點li之后訪問了興趣點lj。每條邊的權重ci，j表示用戶從興趣點li訪問興趣點lj的次數。

本文使用文獻［20］中提出的加權PageRank（Weighted PageRank，WPR）公式計算興趣點lj對用戶u的重要程度：

其中：β∈[0，1]為阻尼系數，可以把它視為其他興趣點對目標興趣點的貢獻；I(lj)表示指向興趣點lj的興趣點的集合；由式（10）計算得出：

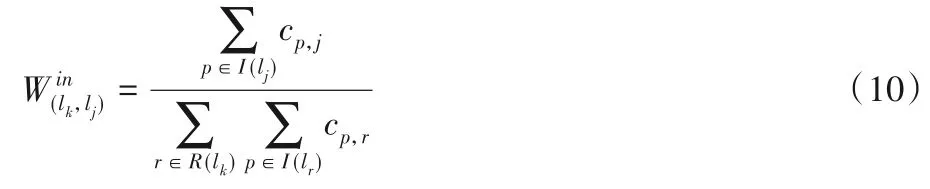
其中R(lk)表表示興趣點lk所指向的興趣點的集合。

3）計算興趣點對用戶的重要程度。

根據式（11）本文將用戶與好友之間的相似程度和興趣點對朋友的重要程度相結合來計算興趣點對用戶的重要程度：

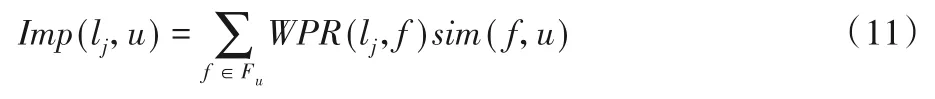
其中Fu表示用戶u的朋友集合。

3.3 興趣點推薦

對用戶的簽到行為進行建模時，本文認為用戶最后簽到決策由兩個因素決定：1）用戶對興趣點的偏好程度；2）興趣點的重要性。當用戶對興趣點的偏好程度越大，并且興趣點對用戶的重要性越高，用戶訪問它的概率越大。因此采用線性組合模型對用戶的偏好和興趣點重要性進行建模，計算用戶u在當前時間段t內對興趣點lj的訪問得分為：

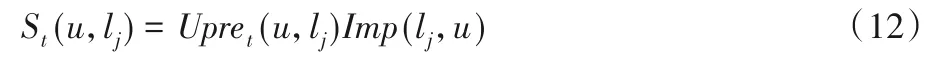
整個RecSI推薦模型偽代碼如算法1所示。

算法1 RecSI推薦模型算法。

輸入：用戶u、用戶集合U、用戶簽到數據集D、興趣點集合L、興趣點類別集合C、用戶u的社交好友集合Fu；

輸出：前K個興趣點組成的推薦列表TOP-K。

4 實驗結果與分析

4.1 實驗數據集

本文算法使用Foursquare 真實的數據集［21］進行評估。通過刪除訪問次數少于10 個興趣點的用戶以及被訪問次數少于10 個用戶的興趣點來對數據集進行預處理。預處理以后數據集包含88 193 個POI 和6 118 個用戶生成的115 890 個簽入，此外數據集中的每個POI都與其經緯度相關聯，并且每個POI 都是由8 個類別和240 個子類別標記。對于每個用戶，按照時間順序對他/她的簽到進行排序，并將前80%的簽到作為訓練數據，20%數據作為測試數據。

4.2 評價指標

本文采用兩個在推薦系統中廣泛使用的評價指標，即精確率Precision@K和召回率Recall@K，指標評價如式（13）、（14）所示：

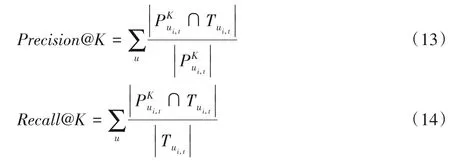
其中：K是推薦列表中興趣點的數量，是用戶在時間t內推薦列表中前K個興趣點的集合，Tui，t是用戶在時間t內訪問過興趣點的集合。本實驗中K設置為5，10，15，20。

4.3 參數選擇

在對興趣點重要性進行建模時，需要確定相似因子α和興趣點重要性參數β的取值：根據α的不同取值可以調節好友社交因子中好友相似性和好友位置相似性所占的比例；β是在計算興趣點重要性中其他興趣點對目標興趣點的貢獻，決定了興趣點之間的轉移概率和網絡的收斂速度。接下來確定兩個參數的選擇。

1）參數α的選擇。

首先固定參數β，然后再選取不同的α值進行TOP-5 的推薦。推薦結果如圖2（a）所示。可以看出，當α=0.5 時，推薦效果最好，因此在后面的實驗中，參數α的值設為0.5。

2）參數β值的選擇。

固定參數α的值為0.5，觀察參數β在［0，1］范圍內的變化，如圖2（b）所示。當β=0.6 時，準確率和召回率達到最大值，因此本文將參數β的值設為0.6。

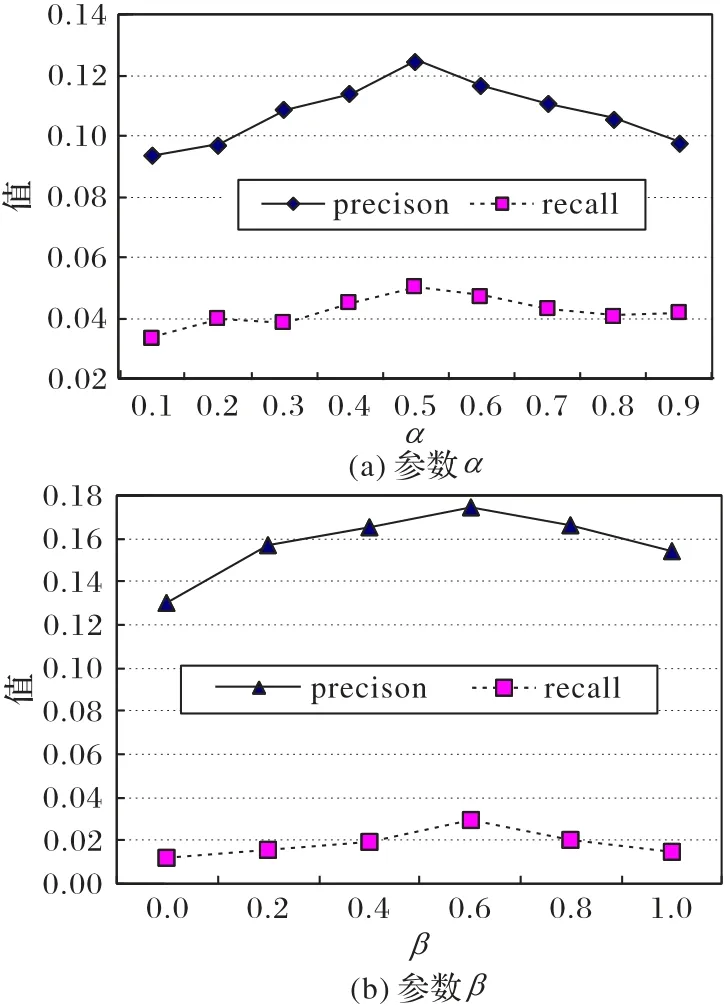
圖2 不同參數對應的準確率和召回率Fig.2 Precision and recall under different parameters

4.4 算法對比

為了驗證本文中提出的模型的性能，選擇以下具有代表行的興趣點推薦方法進行比較：

UPOI-Walk（Urban POI-Walk）模型［15］：融合用戶偏好，社交關系與流行度因素，使用基于HITS（Hyperlink-Induced Topic Search）的隨機游走方法進行興趣點推薦。

TPR-TF（Time-aware POI Recommendation based on Tensor Factorization）模型［11］：利用時間敏感性提出基于層次聚類的時間動態分類算法，將時間敏感性和用戶的朋友影響相結合進行興趣點推薦。

GCSR （Geography-Category-Socialsentiment fusion Recommendation）模型［17］：融合了分類流行度偏好、地理位置、社交關系與情感傾向因素的興趣點推薦。

UTE+SE（User with Temporal preference and smoothing Enhancement+Spacial influence with popularity Enhancement）模型［22］：利用用戶時間增強和空間流行度增強相結合的方法建立混合興趣點推薦模型。

五種推薦模型算法在準確率和召回率的實驗結果如圖3（a）和圖3（b）所示。

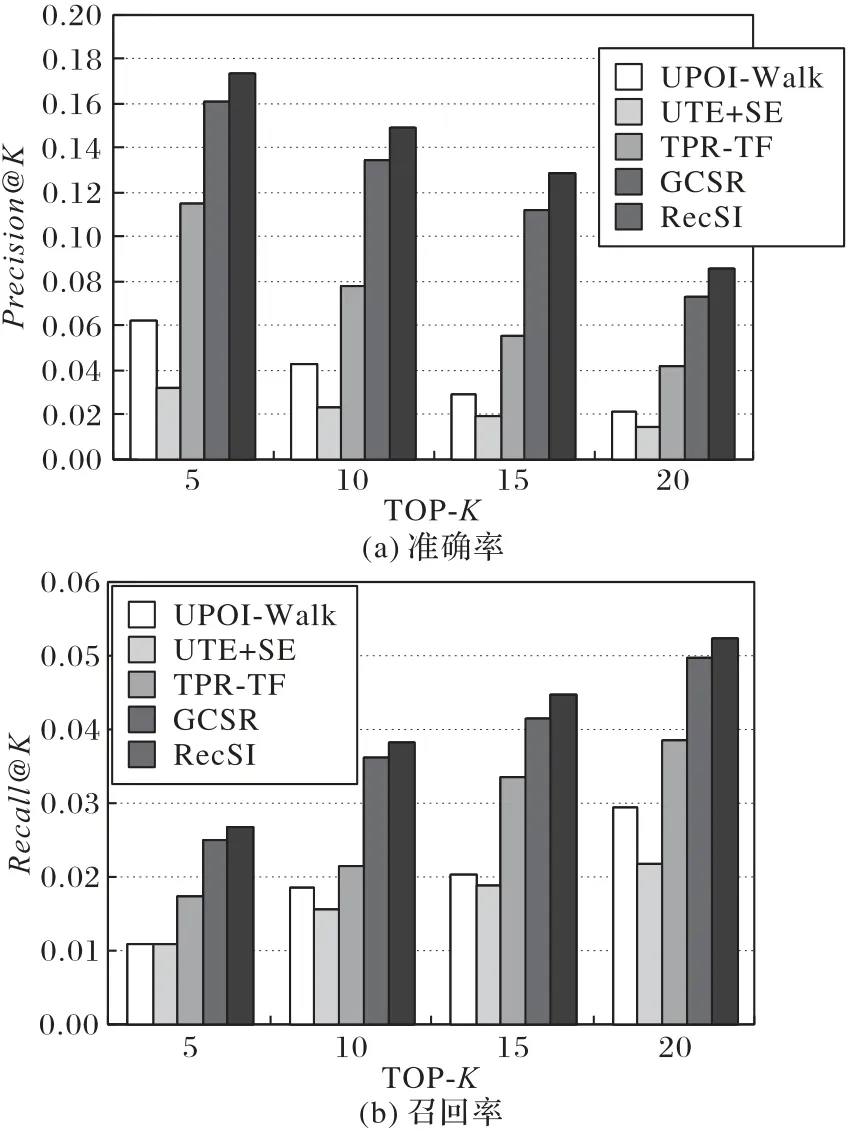
圖3 五種推薦模型的對比實驗結果Fig.3 Comparison experimental results of five recommendation models

從圖3（a）和圖3（b）可以看出，本文提出的RecSI 模型的精確率和召回率都優于其他模型。在幾個方法中，UTE+SE模型將時間和空間影響融合到興趣點推薦中，利用相似時間槽內時間的相似性，結合平滑技術，在一定程度上緩解了數據稀疏性問題，但是推薦的性能并沒有得到很大的改善，因此在對比模型中的準確率和召回率最低。US 模型將用戶偏好、社交關系與流行度因素納入到興趣點推薦中，因此相比UTE+SE 模型，在準確率和召回率都有了很大的提升，但是與RecSI模型相比，由于沒有考慮地理位置和興趣點重要性對推薦結果影響，所以準確率和召回率的提高受到了限制。TPR-TF 模型通過時間敏感性，直接將時間作為特征向量融入到推薦模型中，同時考慮了社交關系中的直接朋友和間接朋友的影響，與US 模型相比，TPR-TF 模型考慮了時間的敏感性，因此推薦的結果有一定程度的提升，但是相比RecSI 模型，因為所使用到的影響因素相對較少，所以模型的準確率和召回率都受到了一定程度的影響。GCSR 模型不僅將地理信息、社交信息、興趣點種類信息加入興趣點推薦中，還融入了用戶的評論信息，考慮用戶的情感傾向，所以相對TPR-TF 模型準確率和召回率有很大程度的提高，但是與RecSI 模型相比，GCSR 模型沒考慮時間因素和興趣點的重要性，因此推薦的準確率和召回率相對較低。RecSI 模型不僅考慮時間因素、地理位置、興趣點類別以及興趣點流行度，同時將社交關系與興趣點重要性相融合，因此推薦的準確率和召回率最好。

5 結語

在本文中提出了融合時間地理信息和興趣點重要性的POI推薦算法（RecSI）。通過興趣點的地理位置和相互之間的吸引力去除數據集中噪聲POI，減少推薦過程中的噪聲困擾，將用戶的動態偏好和興趣點的重要性結合納入推薦框架中，同時引入時間信息、興趣點類別信息、流行度和社交信息，實現在當前時間為目標用戶推薦新的興趣點集。通過在Foursquare 數據集上與其他推薦算法相比，驗證了RecSI 模型的準確率和召回率都有所提高。在未來的工作希望將其他的上下文信息（例如：文本信息）加入到本文的模型中，以研究其對推薦結果的影響。