基于R藤的Copula模型選擇及應用
劉春婷


摘要:在實際生活中,高維數據的情形較多,常用的研究數據間相關關系的方法大多為傳統的線性回歸模型以及Logistic回歸等,處理高維數據的方法涉及較少。基于上述分析,本文考慮采用Copula建模方法對高維數據進行分析,在Copula建模中較為重要的一點是對模型進行選擇。因此本文考慮采用Copula模型中的R藤結構進行研究,通過選用貪婪算法來對R藤的模型結構進行選擇,即對節點和Copula對函數類型進行確定。為了驗證這一方法的可行性及適用性,通過陜西省城鎮居民的消費數據進行實證研究,并得出相關結論。
關鍵詞:高維數據;Copula函數;模型選擇;相關關系
中圖分類號:TP18 ? ? ? ? ? ?文獻標識碼:A
文章編號:1009-3044(2020)17-0222-03
隨著時代的發展,越來越多的數據信息所產生,選擇有效的方法對數據進行分析是至關重要的。Copula函數主要是用于刻畫多個變量間的相關關系的,它不僅可以刻畫協變量對響應變量的影響,還能夠刻畫協變量間的相關關系,克服了傳統方法模型單一對數據中的信息挖掘不到位的缺點。Copula建模方法主要是選用不同的連接方式進行建模,常見的有C藤、D藤以及R藤,其中相比C藤和D藤而言R藤具有較高的靈活性,能夠更加準確地描述變量間的相關關系,但是其涉及的連接種類多,計算量大成為了這一模型的難點。為了克服這一難點,本文考慮采用貪婪算法對R藤的結構進行選擇。關鍵包含兩個方面,一方面是對節點進行選擇,即變量的位置關系進行選擇,另一方面是對每兩個節點間的Copula函數類型進行確定。
在Copula理論的發展過程中,它被廣泛地應用到金融保險、投資組合以及風險預測等各個領域中,Rockinger和Jondeau(2001)[1]建立了Copula-GARCH模型對金融數據進行分析;杜子平(2009)[2]等將動態Copula和高維Vine Copula進行結合從而對不同國家證券市場間的關系進行分析。本文利用貪婪算法對Copula建模方法中R藤的模型結構進行選擇,能夠較快地得出R藤的具體模型結構,有效地降低了R藤模型算法的計算復雜度。
消費結構反映了一個地區的消費水平,也決定了當地人民的生活水平,具有較大的研究意義。近幾年來,陜西省的綜合實力不斷上升,居民的消費水平也在發生著重要的變化,消費結構由較多的變量組成,為了更好地看出消費的各項指標間的相關關系,本文擬考慮采用刻畫變量間相關關系具有極大優勢的Copula建模方法進行研究,R藤的高度靈活性正好適用于這一實際問題。本文基于Copula建模方法采用R藤的方式進行建模,并對陜西省2009年至2018年的城鎮居民消費數據進行研究。
1 相關理論基礎
Copula函數是Sklar[3]在1959年提出的,他提出可以將一個多維的聯合分布函數分解成多個邊緣分布函數和一個連接函數,Copula函數就稱為這個連接函數,通過該連接函數作為橋梁把邊緣分布函數和聯合分布函數進行連接。
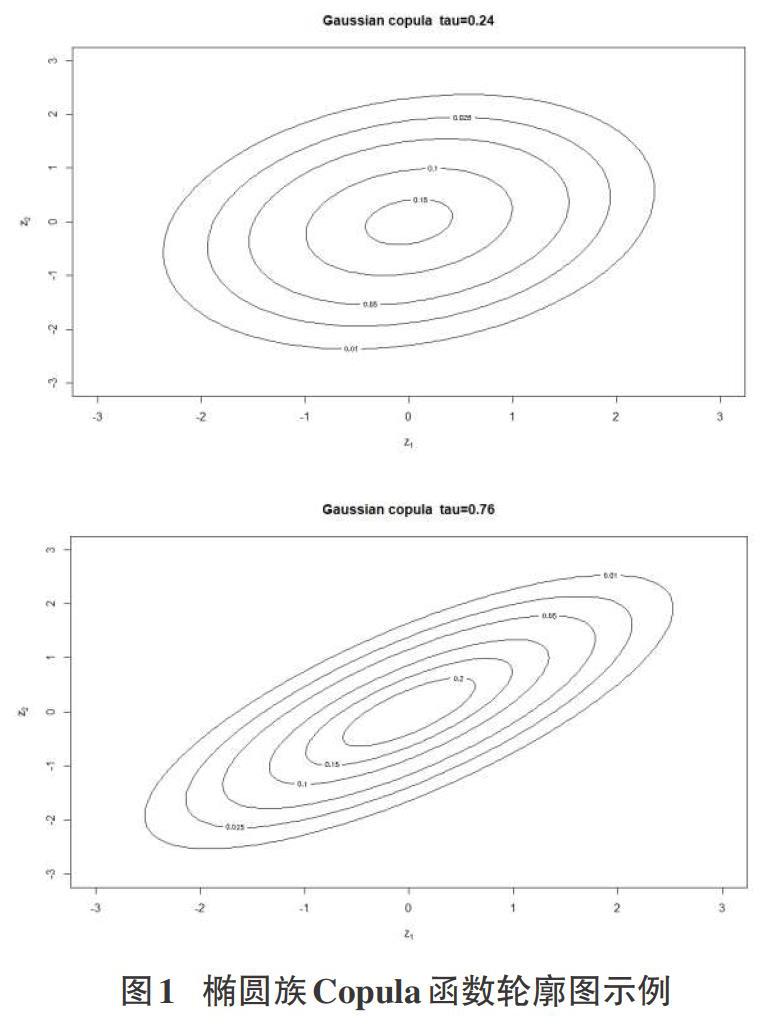
結合上述分析,將Copula函數進行分類,主要包含橢圓族Copula函數和阿基米德Copula函數兩大類,它們用于刻畫不同的數據特征,其中橢圓族Copula函數具有尾部對稱的特點,其對應的輪廓圖如下圖1所示。
阿基米德族Copula函數尾部具有非對稱性的特點,其對應的輪廓圖如下圖2所示。
因此對于不同的數據特征,要選用恰當的Copula函數類型進行刻畫,這是R藤的模型建立過程中的一個難點。
Bedford & Cooke[4]于1999年提出,可以采用樹的結構方式來直觀的描述變量間的連接形式。其中用節點來表示變量,兩個節點間的連線表示的是所選擇的Copula函數類型。不同的連接方式得到不同結構的樹,把這些樹叫作規則藤,即R藤。R藤表現形式不按照一定的規則對節點間的位置關系進行排序,為了更加直觀的進行說明,以一個4維變量為例,給出其中一種類型的R藤的表現形式。
對上式中的參數進行估計,主要采用分兩步極大似然估計的方法,首先,對邊緣分布函數中的參數進行極大似然估計,其次將邊緣分布的參數估計結果帶回,再利用極大似然估計對聯合分布函數中的參數進行估計。
2 基于貪婪算法的模型選擇
2013年,Dissman等人提出了一類處理高維離散型數據的貪婪算法[5]的方法,受該方法的啟發,將該方法應用到數據為連續型的形勢下,該算法的基本步驟如下。
1)估計邊緣分布函數的參數
2) 從低階節點出發,分別計算低階節點涉及的所有的Copula對類型及參數值,進而以修正的赤池信息準則mAIC(modify Akaike Information Criterion)為判別標準,進一步篩選出節點間所有可能的結合方式當中最優的模型,再以上述最優模型的節點連接方式所得到的兩兩Copula對為下一步的起點。
3) 重復上述過程,直至將第[n-1]棵樹的相關節點間的結合方式及每條邊對應的Copula對類型確定。
3 實例分析
通過上述分析可知,Copula函數主要是用于對高維數據進行分析的,當數據的個數較多時,單一的考慮每個指標的變化規律不能夠很好的刻畫實際問題,因此可以通過Copula函數來考慮不同指標間的相關關系。陜西省城鎮居民的消費結構由8個指標組成,那么除了單一的研究每年指標的變化規律外,觀察不同指標間的相關關系是十分具有價值的。因此本文選取陜西省2009年至2018年的城鎮居民消費數據,其中包含如下8個指標。
各個指標是如何發展的,通過如下變化趨勢圖能夠直觀的得出結果。
從圖4只能大致看出各項指標的發展趨勢以及發展趨勢的強度,但是具體不同指標之間是否有相關關系,值得進一步研究。通過對數據觀察不難發現,指標的個數較多,且數據大多呈現出不對稱的特征,因此采用本文所建立的處理高維數據的Copula函數模型是極具優勢的。為了更加全面的分析各指標間的相關關系,將年份也作為一個變量進行研究,同時對9個變量進行分析,通過貪婪算法對R藤的模型結構進行選擇,所得到的結果如下圖5所示。
圖5為通過貪婪算法對Copula建模方法下的R藤的選擇結果,本文主要研究第一層樹,即對不同變量間的關系進行刻畫。其中圖的左下方描述的是所選用的Copula函數擬合出的輪廓圖,從圖上可以看出,指標衣著與醫療保健、交通通訊與文教娛樂與通訊等指標對之間呈現出較強的尾部對稱性,并且從輪廓圖的形狀上來看,越扁的說明兩個指標的相關性越強。圖的右上方這些數字刻畫了每兩個變量間的相關性強弱,相關性越強這個紅色的字體越大并且對應的數的絕對值越接近于1,相關性越弱,對應的數的絕對值越接近于0。為了更加直觀的得出不同指標間的相關關系,給出具體數值見表2。
表2 詳細地給出了每兩個變量間的相關關系結果,由表中數據易得,(1)變量1年份與任意指標之間都具有較高的相關性,尤其是與食品和衣著這兩個變量,呈現出較高的正相關性,說明人們的生活水平在不斷提高,大家對衣著和食品方面的支出越來越大。(2)食品與家庭設備及服務這兩項指標之間呈現出負相關性,且kendall [τ]值為-0.63,說明相關程度較高;并且衣著與家庭設備及服務這兩項指標也呈現出負相關性,說明家庭設備及服務該指標的增長速度與它們之間是呈現負相關關系的。(3)醫療保健和交通通訊、文化娛樂及服務以及雜項商品及服務、醫療保健與文教娛樂及服務等等,它們之間都呈現出較高的正相關性,相關性都較強。(4)觀察不難發現,居住這項指標與各指標間的關系均不是太強,但是它的增長幅度從數據中可以看出,具有較大的增長幅度,說明該項指標不受其他因素的影響,自身的漲幅較大,說明大家對居住越來越重視。
參考文獻:
[1] Coutant S,Jondeau E,Rockinger M.Reading PIBOR futures options smiles:The 1997 snap election[J].Journal of Banking & Finance,2001,25(11):1957-1987.
[2] 杜子平,閆鵬,張勇.基于“藤”結構的高維動態Copula的構建[J].數學的實踐與認識,2009,39(10):96-102.
[3] Genest C,MacKay J.The joy of copulas:bivariate distributions with uniform marginals[J].The American Statistician, 1986,40(4):280.
[4] St?ber J,Joe H,Czado C.Simplified pair copula constructions—Limitations and extensions[J].Journal of Multivariate Analysis, 2013,119:101-118.
[5] 常友渠,肖貴元,曾敏.貪心算法的探討與研究[J].重慶電力高等專科學校學報,2008,13(3):40-42,47.
【通聯編輯:唐一東】

