超聲速巡航導彈速度控制系統設計

邱志強,廖選平,孫瑞勝,朱 斌

(南京理工大學 能源與動力工程學院,江蘇 南京 210094)

現代戰爭中戰役戰術導彈要具備大空域、多彈道、遠射程、大機動的作戰性能特點,超聲速巡航導彈以其具有飛行包絡大,能夠適應各種戰場需求的特點[1],成為了各個國家的研究熱點之一。固體沖壓發動機結構簡單,質量輕,推重比大,成本低,具有較高的經濟性[2],多被應用于超聲速巡航導彈[3]。

清楚認識被控對象的工作特性是設計控制器的基礎。從固體沖壓發動機的工作原理和系統組成出發,文獻[4]分析了燃氣發生器的穩態和非穩態過程,通過數值模擬研究得到了自由容積和燃速壓強指數對流場的影響;文獻[5]通過數值模擬得到了燃燒室入口開度、燃燒室幾何大小對固體沖壓發動機工作的影響。針對固體沖壓發動機的建模問題,學者們做了大量的研究。基于多變量變化的燃燒效率模型,文獻[6]提出了發動機工作過程的模型;文獻[7]則建立了一種能夠對推力進行預測的燃氣流量可調的固體沖壓發動機模型;另外,通過影響系數法,文獻[8]建立了沖壓發動機的準一維模型。目前,多數研究僅針對固體沖壓發動機本身,關于超聲速巡航導彈速度控制系統的模型研究相對較少。

準確地控制固體沖壓發動機的工作過程是超聲速巡航導彈的速度控制的關鍵。固體沖壓發動機的控制方法大多采用PID控制[9-10],但固體沖壓發動機工作過程迅速,存在負調節等復雜現象[11],同時固體沖壓發動機模型本身存在非線性及不確定性[12],這些都給超聲速巡航導彈的速度控制系統設計帶來了一定的困難,傳統PID控制已不適用。因此,尋找合適的控制方法是超聲速巡航導彈速度控制系統設計的關鍵。反演控制技術是近年發展起來的一種非線性反饋控制設計的方法。反演控制技術引入“虛擬控制量”,分別設計其控制律,最終獲得系統實際的控制輸入[13]。但當系統模型存在不確定性時,反演設計方法的魯棒性能將不再滿足要求。為此,國內外學者將反演控制方法結合自適應控制與滑模控制等,取得了良好的控制結果[14-16]。

本文以超聲速巡航導彈為研究對象,結合固體沖壓發動機的工作特性,分析并建立了超聲速巡航導彈的速度控制系統數學模型。針對速度控制系統存在的參數時變和不確定干擾問題,在反演法的基礎上設計了一種反演魯棒控制器,利用Lyapunov理論驗證其穩定性。通過與PID控制方法的仿真對比,驗證控制器設計的可行性及有效性。

1 問題描述

1.1 速度控制系統數學模型

如圖1所示,超聲速巡航導彈的固體沖壓發生器相當于一個固體火箭發動機,但又有別于固體火箭發動機。發動機工作過程中,由燃氣發生器產生高溫高速的燃氣射流噴入沖壓補燃室與沖壓空氣進行摻混增壓,燃氣從尾噴管噴出產生推力[17]。

圖1 固體沖壓發動機結構示意圖

因此,為滿足超聲速巡航導彈的推力需求和實際的飛行條件,需要調節圖1中的壅塞調節閥開度,改變發動機所產生的推力。

燃氣發生器內的質量守恒方程:

(1)

式中:qm,r為燃氣發生器內產生的燃氣質量流量;qm,g為燃氣發生器噴管排出的燃氣質量流量;d(ρrVr)/dt為燃氣發生器內燃氣質量隨時間的變化,ρr為推進劑燃燒產生的燃氣密度,Vr為燃氣發生器的自由容積。其中燃氣發生器自由容積的變化可由推進劑燃燒減少的體積表示,即

(2)

式中:Vr0為燃氣發生器初始自由容積,a為燃速系數,Sb為燃燒面積,pr為燃燒室燃氣壓力,n為壓力指數。

將式(1)展開推導,具體過程見文獻[18],可得固體沖壓發動機燃氣發生器內彈道方程:

(3)

在亞燃固體沖壓發動機中,由于實際產生的推力不易測量且氣體通過沖壓補燃室的壓力基本恒定[19],可將沖壓補燃室的入口壓力,即燃燒室燃氣壓力pr,經換算近似等效為推力Fp。因此有

Fp=Sipr

(4)

式中:Si為噴管面積。

超聲速巡航導彈飛行速度除受推力Fp影響外,還受阻力Fx和重力G的影響,如圖2所示,圖中,v為超聲速巡航導彈的飛行速度,α為攻角,θ為彈道傾角。

圖2 超聲速巡航導彈受力示意圖

根據導彈的動力學關系[20],在不考慮導彈的側向及滾轉通道的情況下,導彈的縱向動力學方程為

(5)

式中:m為導彈質量。阻力Fx是由動壓q、阻力系數cx和特征面積S構成的函數,表示為

Fx=cxqS

(6)

假設導彈飛行過程中做α,θ均近似為0的水平直線運動,由于動壓q=ρv2/2,ρ為大氣密度,式(5)可改寫為

(7)

在導彈動力學關系中考慮固體沖壓發動機工作特性,建立理想情況超聲速巡航導彈速度控制系統的數學模型:

(8)

1.2 速度控制系統控制模型

X=(x1x2)=(vpr)

(9)

噴喉面積St作為系統控制輸入量u,可以得到速度控制系統的狀態空間形式:

(10)

2 控制器設計

本文設計反演魯棒控制律的基本思路為:首先利用傳統反演法的思想推導得到滿足導彈飛行速度增量所需期望推力Fp,d,然后設計魯棒控制律控制燃氣發生器喉部面積St,產生趨向于期望推力的實際推力,從而跟蹤速度指令vc。

2.1 速度控制器設計

對于速度控制系統(10)中子系統1,定義速度跟蹤誤差為e1,參考速度為x1,d,則

e1=x1,d-x1

(11)

且

(12)

定義Lyapunov函數為

(13)

對式(13)求導得:

(14)

將式(12)代入式(14)有

鄒先生說，秦檜死后，陸游 “急于出仕的心跡，在這首詩中表現得最為明顯” ，并將這首作于紹興二十六年(1156)冬的詩， “不妨看作是陸游出仕前向云門的告別”。既然鄒先生將這首詩看作是“告別”之作，那么紹興二十七年(1157)春，陸游就應該出仕的了。因此，鄒先生緊接著說“這里涉及《送陳德邵宮教赴行在二十韻》《朱子云園中觀花》《酬妙湛闍梨見贈》《次韻魯山新居絕句》《寄陳魯山》等詩的編排問題，筆者(鄒志方)以為，這些詩均作于出仕前，即紹興二十六年冬日前。” ⑥然而，查錢仲聯先生《劍南詩稿校注》(上海古籍出版社2005年版)，這些詩均在紹興二十七年(1157)作于山陰。

(15)

(16)

式中:控制器可調控制參數k>0,且k∈R。定義控制系統的推力誤差為e2,則

e2=x2,d-x2

(17)

且

(18)

由于傳統滑模控制存在抖振現象,為避免出現抖振,本文設計如下具有高頻反饋魯棒控制的速度控制算法:

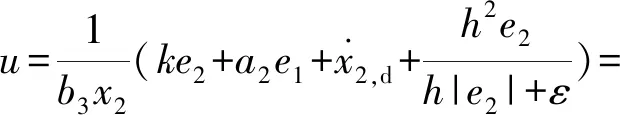
(19)

式中:控制器可調控制參數ε>0,ε∈R;h表示不確定系統的正上界函數。在該控制算法控制下,速度控制系統能夠實現超聲速巡航導彈的速度控制并且保證最終速度誤差有界。

2.2 穩定性分析

定義Lyapunov函數為

(20)

對式(20)求導得:

(21)

將式(17)代入式(21)并展開得:

(22)

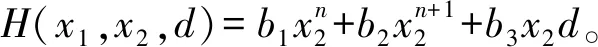
(23)

設計h,使得h≥|H(x1,x2,d)|,將式(23)進行放縮,過程如下:

(24)

由于

(25)

將式(25)代入式(24)則有

(26)

求解微分不等式(26),可以得到Ve1,e2(t)的上界:

(27)

求Ve1,e2(t)終值:

(28)

因此,將式(20)代入式(28),由Lyapunov穩定性理論知,最終系統誤差滿足:

(29)

由式(29)可知,當經過時間充分長后,系統誤差的界與初始狀態無關,即速度控制系統的誤差可以達到全局一致最終有界(GUUB)。

3 仿真分析

為驗證所提出的反演魯棒控制方法的可行性及有效性,本文以某超聲速巡航導彈為例設計反演魯棒控制律進行仿真,并與傳統PID控制進行對比分析研究。傳統PID控制器控制律設計為

(30)

式中:kp為比例系數,ki為積分系數,kd為微分系數。

3.1 標稱模型下的數值仿真

圖3給出了標稱模型條件下反演魯棒控制器和PID控制器響應速度指令的曲線,圖4給出了速度跟蹤誤差曲線,圖5給出了燃氣發生器自由容積變化曲線。從圖中可以看出,隨著時間增加,燃氣發生器自由容積不斷增大,速度控制系統模型參數將逐漸偏離初始時刻。PID控制系統存在明顯相位滯后且由于參數變化的影響導致控制效果逐漸變差;而反演魯棒控制能夠在全過程中準確地跟蹤指令信號,跟蹤效果明顯優于PID控制,受模型參數變化影響較小。

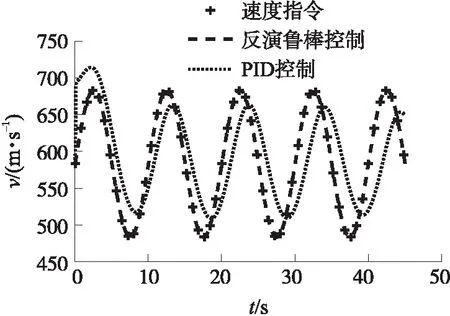
圖3 標稱模型下的速度響應曲線

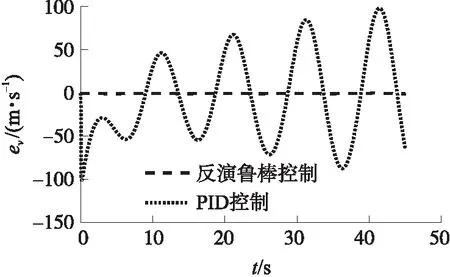
圖4 標稱模型下的速度誤差曲線

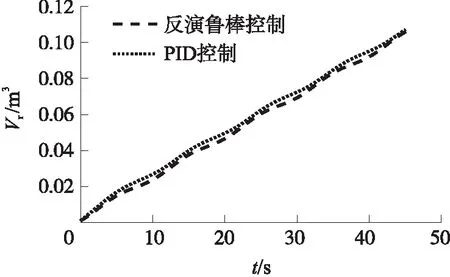
圖5 標稱模型下的自由容積變化曲線

圖6給出了固體沖壓發動機噴喉面積變化曲線。從圖中可以看出,反演魯棒控制的控制量響應速度明顯快于PID控制,并且未出現抖振現象。

圖6 標稱模型下的噴喉面積變化曲線

圖7、圖8分別給出了固體沖壓發動機壓強變化曲線和流量變化曲線,由圖可見,反演魯棒控制的壓強和流量變化較為快速、穩定。

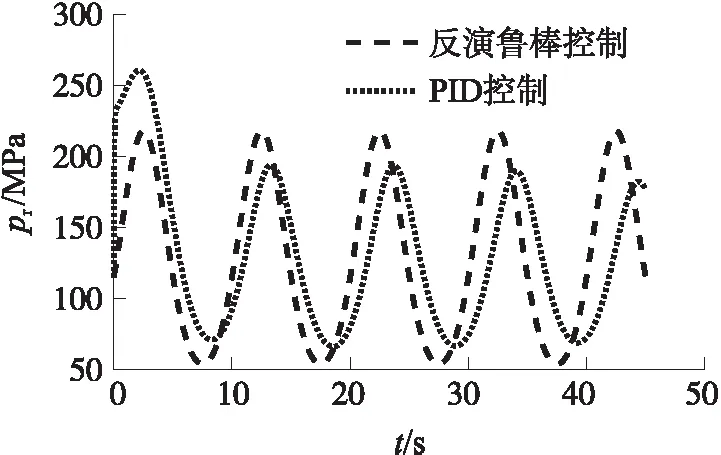
圖7 標稱模型下的壓強變化曲線

圖8 標稱模型下的流量變化曲線

3.2 存在干擾的數值仿真

假定超聲速巡航導彈維持勻速巡飛,v=583.2 m/s,在15 s時由于壅塞調節閥被燒蝕,噴喉面積瞬間擴大2×10-5m2。對突變的外部擾動進行模擬,圖9給出了此時的速度變化曲線,圖10給出了受干擾的速度誤差曲線。由圖可知,PID控制系統受此干擾影響,出現25 m/s的速度誤差;而反演魯棒控制系統受此干擾影響,僅產生不到0.5 m/s的速度誤差,抗干擾能力明顯較強。

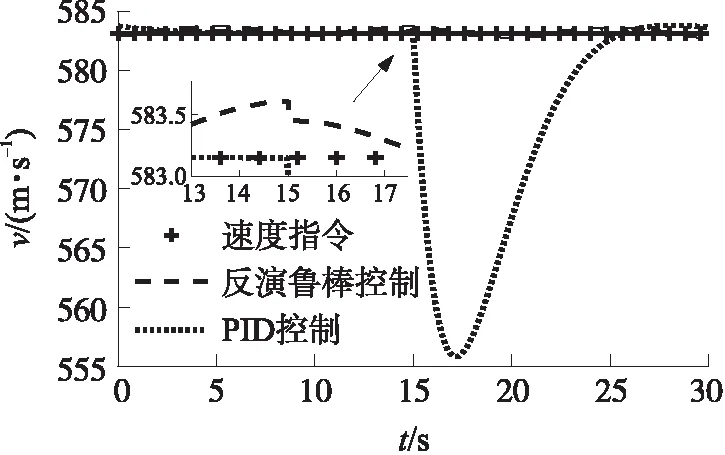
圖9 受干擾的速度響應曲線

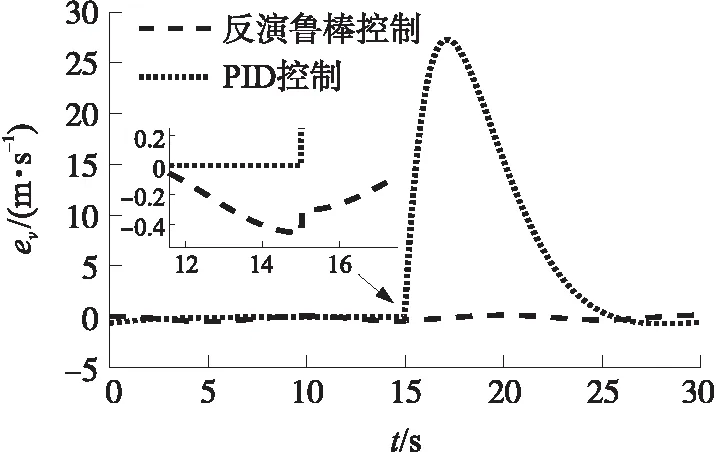
圖10 受干擾的速度誤差曲線

圖11～圖13給出了此時固體沖壓發動機的工作過程變化曲線。由圖可以看出,反演魯棒控制系統在受到外界干擾后能夠迅速調節噴喉面積,彌補被燒蝕部分產生的影響,使壓強和流量在短時間內恢復原本狀態,維持導彈巡飛速度。

圖11 受干擾的噴喉面積變化曲線

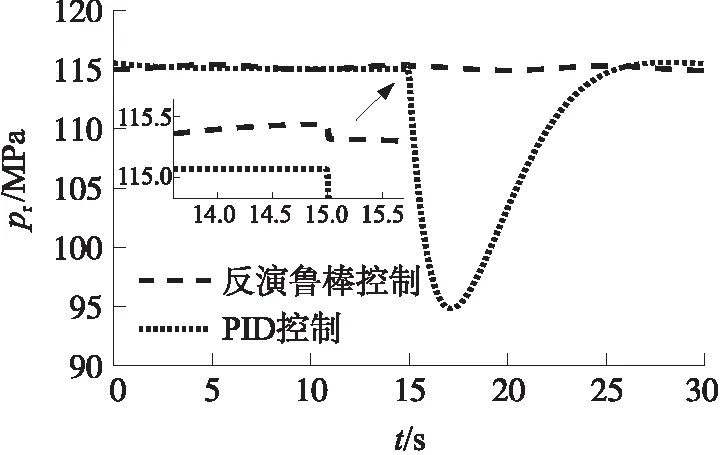
圖12 受干擾的壓強變化曲線

圖13 受干擾的流量變化曲線

4 結論

本文根據超聲速巡航導彈飛行動力學關系,結合固體沖壓發動機的工作特性建立了超聲速巡航導彈速度控制系統模型。由于速度控制系統存在參數時變、不確定干擾等問題,采用傳統的PID控制難以滿足導彈巡航過程的速度需求。本文在反演法的基礎上,有效地結合了反演控制和魯棒控制的優點,設計了復合型反演魯棒控制器,通過模擬仿真驗證其控制效果。在標稱模型仿真條件下,傳統控制方法速度誤差達到50～100 m/s,反演魯棒控制器控制速度誤差小于0.5 m/s。超聲速巡航導彈固體沖壓發動機實際工作過程中響應時間較慢,仿真結果中受擾動影響速度控制系統響應時間小于0.1 s,而目前固體沖壓發動機響應需要3～8 s。仿真結果表明,本文提出的控制算法能夠快速精確地跟蹤目標指令,同時具有較強的魯棒性。