激活思維，提升能力
——一節數學課的教學改進與思考

（桐鄉市洲泉中學，浙江 嘉興 315000）

學生在數學學習的過程中經常會出現各種思維障礙，其原因是多方面的，但主要的原因是數學課堂中大量存在著缺少學生參與數學思維活動的現象，往往略去了知識的探究過程，取而代之的是教師一言堂和機械的訓練。尤其是優等生缺乏對知識的“火熱”思考和主動建構，因而思維能力的提升就無從談起。《新課標》指出，數學教育既要使學生掌握現代生活和學習中所需要的數學知識和技能，更要發揮數學在培養人的思維能力和創新能力方面的不可替代的作用。數學教學活動，特別是課堂教學應激發學生興趣，調動學生積極性，引發學生的數學思考，要注重培養學生良好的數學學習習慣，使學生掌握恰當的數學學習方法。為此，我校對九年級學生實施分層教學，給優等生創造了一個良好的課堂學習氛圍，同時也為數學教師們提供了分層教學的環境。

一、留足時間，打開思維通道

陶行知認為，在初中數學教學中，教師要留給學生動腦的機會，讓學生有較充分的思考時間和空間，發表自己的見解，這樣才有助于培養學生的探究精神，訓練學生的創新思維能力。優等生除了掌握基本的知識和概念以外，更應該注重能力的培養，課堂是培養優等生思維能力的最佳基地。

下面以《浙教版九下數學§2.1 直線與圓的位置關系（1）》中的例5、例6 為例，通過兩種教學方式的比較，來驗證：在數學課堂的教學中，把時間還給學生，更有助于激發學生的思維，打開學生的思維通道。

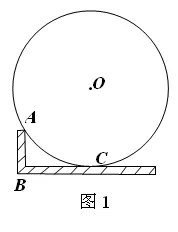
例5 木工師傅可以用角尺測量并計算圓的半徑.如圖1，用角尺的較短邊緊靠⊙O于點A，并使較長邊與⊙O相切于點C.記角尺的直角頂點為B，量得AB=8cm，BC=16cm。求⊙O 的半徑.

（一）克扣時間，效果不佳

在之前的教學中，筆者總是為了能夠順利地完成教學任務，

克扣學生的思考時間，便迫不及待地在課件中呈現早已設置好的幾個小問題。如例題5 會設置以下幾個問題：

（1）遇到切點，我們往往會將切點與誰連結？（連結圓心和切點）；

（2）求半徑長度，可構造哪一種圖形？

（3）當圖形中出現多個直角時，可構造哪一種特殊四邊形？

通過這種逐步引導的方式來幫助學生形成解題思路，最終通過師生的短暫互動得到下面“方法二”的解題過程，以致優等生朝著教師課前設置好的思路走下去。這樣雖能完成教學進度，但學生沒有了自己的思考時間和空間，久而久之會對老師產生依賴心理，導致學生在做作業時，一旦沒有教師在旁指點一二，便不能夠很好地完成有難度的習題。

（二）放手一搏，喜出望外

暫停講解，先給學生足夠時間思考，接著傾聽他們的思考過程和結果，再進行點評和引導。

經過5 分鐘的思考，學生首先提供的是下面的方法一

（我很茫然，輔助線添加得也太多了一點，但我還是打算耐心地聽一聽）

師：生3很棒，大家的想法也很默契！那么同學們還有其他的解決方法嗎？

（停頓了一會兒后，見學生們沒有思緒，稍作提示。）

師：同學們的剛才的解決方法使通過相似三角形的性質求出半徑的，那求線段的長度除了這個方法外，還有哪一種更常用的方法呢？……

生4：勾股定理

師：很好，那如何來構造這個直角三角形呢？請同學們結合題中的條件再次思考。最后在大家的相互協作下，完成了下面的“方法二”。

通過課后反饋，學生首先想到的是用勾股定理求出線段AC 的長；接著根據AC 在圓中扮演“弦”的角色，又因為所求的是圓的“半徑”，自然而然想到了垂徑定理，還有部分學生運用的是等腰三角形三線合一性質，故而如此添加輔助線；再根據多個直角（∠B，∠OCB），并結合圖形，又進一步聯想到了K 字形相似，從而解決了問題（即方法一）。可見學生的想法自然，清晰到位，并且計算簡單，并不遜色于書本提供的方法。若教師一味地牽著學生的鼻子走，不但不利于學生智力的開發，還會大大打擊學生們的學習自主性。接著以相同的課堂教學方式，分析并完成了例6 的教學。

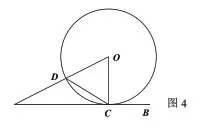
例6 已知如圖,4，直線AB 與⊙O 相切于點C，AO 交⊙O 于點D，連結OC，CD.求證：（注：幾何知識中倍角關系的證明是一個重要的知識點，學生急需掌握相應的解題思路和方法。）

課堂上給優等生充足的時間和空間，有利于激發他們去發現和去創造的強烈欲望，加深他們對所學知識的深刻理解，訓練他們對數學思想和數學方法的嫻熟運用，鍛煉他們思維的廣闊性和深刻性、靈活性和獨創性，從而培養他們的思維品質。

二、及時總結，把握思維方向

及時總結可以幫助優等生理清所學知識的層次結構，掌握其外在的形式和內在聯系，形成知識系列及一定的結構框架。通過對所解問題的及時總結，可以幫助優等生掌握解題的方法和經驗，從而提高他們的思維能力。

課堂教學中，當學生被激發出多種思維解決同一問題以后，一定要采取及時總結的措施，幫助學生一起整理解決問題的思路和方法，讓他們的能力更加精進。經過長期的訓練，會讓優等生養成及時總結的良好習慣，有助于他們在做習題的過程中把握思維的方向，有效地解決問題。

對于方法的總結要簡潔、準確，把握解題的中心，因此我采用“希沃爾技術”呈現解題方法的詳細過程，便于優等生回憶解題過程；再借助“學科思維導圖”整理各種方法的解題思路，便于學生進行比較和總結，讓學生能夠根據所求問題，掌握解題的技巧，積累解題的經驗。

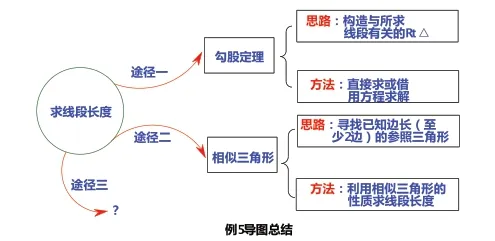
（一）總結例5，把握求線段長度的思維方向

師：請同學們根據上述兩個方法的解題思路，請思考一個問題：當我們再次遇到有關求線段長度的問題時，可從哪些方向入手去尋找問題所需的條件，然后根據題中各個已知條件展開合情推理，找到問題解決的思路和方法呢？

結合剛剛的思路整理，采用“逆推”的方式，借助思維導圖，便能簡潔、清晰地展示求線段長度的基本思路和方向。通過這樣的方式進行整理和總結，讓學生掌握及時總結的方法。

任務：請同學們在課后翻閱做過的類似習題，找找還有沒有其他方法可用來求線段的長度，并進一步完善“求線段長度”的思維導圖。通過對方法的整理和歸類，有助于優等生今后更加有效地落實課堂和課后作業，幫助他們減輕學業負擔，從而能騰出更多的時間去思考、去鉆研，讓他們的能力得到進一步的提升。

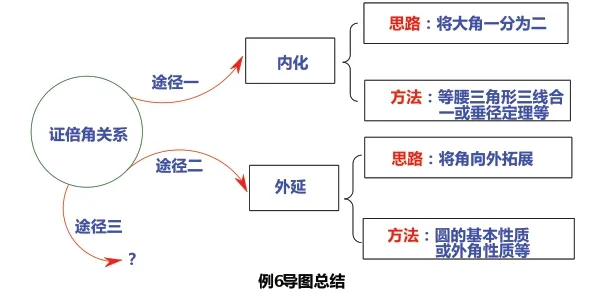
（二）總結例6，把握證倍角關系的思維方向

證明倍角關系是初中數學幾何中的一塊重要內容，因此把握思維方向，掌握方法很重要，那么證明倍角關系又有哪些思維方向呢？先結合例6 的兩種方法，進行思路整理。再讓學生根據上述兩幅思維導讀，并結合例5 思維導圖的方法，完成右圖這一幅有關倍角關系證明的導圖。

通過對證倍角關系思維和方法的總結，有助于優等生加強幾何問題的證明和邏輯思維的培養。

首先根據解題方法縷清思路，再用逆向思維總結方法，是初中數學常用的學習方法。要讓學生具備這樣的能力，及時總結必不可少。一旦養成良好的總結習慣，可為優等生今后的數學學習和研究、能力的鍛煉打下堅實的數學基礎。

三、延伸拓展，提升思維能力

知識的延伸拓展和方法的應用，可以有效地促進知識的遷移，同時能提高優等生的學習積極性，培養參與意識；促進知識網絡的形成，架構思維的橋梁，提升優等生的思維能力。

為了讓學生感受到總結的作用，同時檢測剛才的教學是否有效，“延伸拓展”這一環節便可起到一舉兩得之功效。

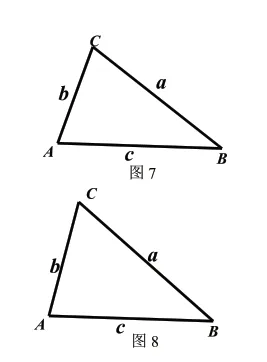
（一）精選習題

（2）如圖8，當當∠A ＜90°時，請判斷第（1）小題的結論是否仍成立，并說明理由。

讓學生通過對這個習題的練習，了解在初中數學幾何問題的學習中，可通過倍角關系去證明線段之間的關系，從而掌握知識點之間是相互聯系，不可分割的，它們能組成一個強大的知識網絡。同時讓優等生了解到證線段的關系不光可以從線段本身入手，還可以從角之間的關系、邊角的關系去落實，達到升華思維之目的。

（二）解決問題

優等生有了思考的方向，更應該放手，將課堂再次還給他們，由他們去創造和發揮。先單獨思考，再合作討論，最后由他們通過自己的智慧，去收獲喜悅。

（三）課后作業

請同學們于課后完成下面習題：

（1）求拋物線的表達式；

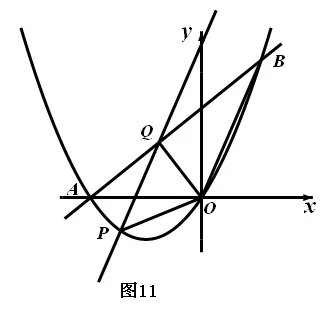
（2）連結OB，點P 為x軸下方拋物線上一動點，過點P 作OB 的平行線交直線AB 于點Q，當S△POQ：S△BOQ=1：2 時，求出點P 的坐標.（坐標平面內兩點M之間的距離

布置這個問題的目的是讓學生通過對第三小題的解答，總結出：我們可以通過作角平分線證倍角關系，那么證倍長關系，可以通過取線段中點，通過類比的方式，找到思維的突破口，把握思維的方向，促成思維能力的提高。

總之，對于初中數學優等生的教學，除了教會他們掌握基本的知識和概念以外，更應注重他們能力的培養。因為只有提高優等生的思維能力，讓他們學會分析問題、解決問題、總結方法、積累經驗并學會運用，才能從根本上解決他們的學業負擔，減輕他們的心理壓力，真正達到“學為中心”、“輕負高效”之目的。