聚合硅酸鐵多相UV-Fenton體系中橙Ⅱ脫色的動力學模型

陳建新,劉治慶,李獻眾,姜自立,劉力章

(1.南昌大學資源環境與化工學院,江西 南昌 330031;2.鄱陽湖環境與資源利用教育部重點實驗室,江西 南昌 330031;3.江西省環境科學研究院,江西 南昌 330077)

高級氧化技術利用強氧化性的·OH能夠將有機污染物完全礦化(有機物被分解成二氧化碳和水)，被認為是有機廢水高效處理技術之一[1-3]。多相UV-Fenton技術是高級氧化技術的一個分支，在有機廢水特別是染料廢水的處理中得到廣泛的關注[4-7]。

催化劑的開發是多相UV-Fenton技術的基礎，其中催化劑活性組分的選擇至關重要，不同的活性組分及其對應的合成方法會最終影響催化劑的催化性能[8-12]。目前，多相UV-Fenton催化劑主要以鐵氧化合物為催化活性組分進行開發[13-14]，對于鐵聚合型催化劑的研究則鮮有報道。作者在前期的研究中發現，聚合硅酸鐵(鐵聚合型活性組分)具有優異的催化性能。相對于鐵氧化合物(α-FeOOH、Fe3O4、γ-Fe2O3)的催化體系，偶氮染料橙Ⅱ完全脫色(染料分子發色或助色基團破壞導致染料溶液色度降低的過程)所需時間在聚合硅酸鐵催化體系中能夠縮短1倍以上。對于聚合硅酸鐵多相UV-Fenton體系，選用合適的擬合方法建立有機污染物的降解動力學模型，不僅能充分評價催化劑的性能，而且能夠精準預測有機污染物的降解(有機化合物分子中的碳原子數目減少、分子量降低的過程)，有望為鐵聚合型催化劑的開發和應用提供理論基礎。

研究表明[11,15]，在羥基自由基氧化體系中，有機污染物的降解符合準一級動力學方程：

(1)

式(1)積分變換為：

(2)

或：

Ct=C0e-kt

(3)

式中，C0為有機污染物的初始濃度，Ct為不同反應時刻有機污染物的濃度；t為反應時間；k為有機污染物降解的準一級動力學常數。

通過式(2)擬合計算動力學常數的過程中，存在全過程擬合和分段擬合兩種方法。全過程擬合法是將有機污染物所有降解數據根據式(2)進行線性擬合，其斜率即為準一級動力學常數k值。利用該值大小可以評判不同氧化體系對有機污染物的降解性能[15-16]，或者通過式(3)對降解體系中有機污染物濃度變化進行準確預測。在均相UV-Fenton體系研究中，全過程擬合法得到廣泛的驗證[1,17]。長期以來，該法也被廣泛應用于多相UV-Fenton體系催化劑活性的評估[11,15,18]。

近年研究發現，在多相UV-Fenton體系中，有機污染物的降解根據催化過程可以劃分為三個階段[9,19-24]：誘導段、快速降解段和慢速降解段。其中，誘導段主要發生催化劑表面鐵離子的活化和釋放過程，有機污染物的降解不明顯[22]；在快速降解段，催化劑表面鐵離子和釋放的鐵離子可以引發多相和均相Fenton反應，導致有機污染物快速降解[20,23]；慢速降解段則以中間降解產物礦化為主，有機污染物降解速度減緩[24]。因此，分段擬合法用于多相UV-Fenton體系更為合適。相對于誘導段和慢速降解段，有機污染物在快速降解段的降解動力學常數通常大一個量級[20]，在一定的條件下可能部分或者完全掩蓋前二者。由此，有機污染物降解的真實分段情況，需要根據不同的多相UV-Fenton體系作具體分析。例如，Wei等構建了鐵-蒙脫石多相光助-芬頓體系，發現苯酚在體系中的降解明顯分為誘導段和快速降解段，兩段擬合的方法能很好模擬苯酚的降解動力學過程[9]；相反，Chen等在UV/TiO2/Fenton復合工藝降解布洛芬的研究中發現，雖然兩段擬合的方法也能精準模擬布洛芬的降解動力學過程，但其降解主要由快速降解段和慢速降解段構成[25]。綜上，對于不同的多相UV-Fenton催化體系，需要先確定有機污染物降解的分段情況，而后選擇合適的擬合方法，才能得到高精度的動力學模型。

本文在分析聚合硅酸鐵多相UV-Fenton體系降解橙Ⅱ過程的基礎上，比較了全過程擬合和兩段擬合兩種方法計算動力學常數的精度，建立并驗證了以催化劑用量和H2O2初始濃度為變量的橙Ⅱ脫色動力學模型，為聚合硅酸鐵多相UV-Fenton體系的應用提供理論基礎。

1 材料與方法

1.1 實驗試劑與儀器

實驗試劑：硅酸鈉、硝酸鐵購于國藥集團化學試劑有限公司；鹽酸、30% H2O2購于西隴科學有限公司；橙Ⅱ(C16H11N2O4SNa，2-萘酚偶氮對苯磺酸鈉)購自阿拉丁。上述試劑均為分析純，實驗室用水為去離子水。實驗儀器：紫外燈管(上海寶山電器儀器廠)；PH400基礎酸度計(上海安萊立思儀器科技有限公司)；V-1600可見分光光度計(上海翱藝儀器有限公司)；UV-2300紫外分光光度計(上海天美科學儀器)。

1.2 試驗方法

聚合硅酸鐵多相UV-Fenton降解橙Ⅱ的實驗在自制光化學反應器中進行[11]，反應體系初始pH值為3.0，橙Ⅱ濃度為0.2 mmo·L-1，磁力攪拌使反應液混合均勻。循環水控制體系恒溫30 ℃，254 nm的紫外燈作為光源。探討聚合硅酸鐵的用量對橙Ⅱ降解過程的影響時，其用量分別取0.25、0.5、0.75和1.0 g·L-1；探討H2O2用量對橙Ⅱ降解過程的影響時，其用量分別取5.0，7.5，10.0和12.5 mmo·L-1。反應之前，聚合硅酸鐵和橙Ⅱ反應液避光磁力攪拌30 min以達到吸附平衡，之后H2O2的加入和紫外燈照射作為多相UV-Fenton反應的起始點，于設定時間點取樣立即通過0.45 μm濾頭過濾、并測定。

1.3 分析方法

橙Ⅱ濃度的測定采用可見分光光度法[26]，全波長掃描用紫外-可見分光光度計測定(UV-2300)，總有機碳采用總有機碳分析儀(2100，Jena分析儀)測定[27]。

2 結果與分析

2.1 聚合硅酸鐵多相UV-Fenton體系中橙Ⅱ的兩段脫色過程

圖1(a)是聚合硅酸鐵多相UV-Fenton體系中橙Ⅱ脫色與礦化過程的比較，圖2(b)是橙Ⅱ脫色過程不同時刻的全波長掃描圖。

根據染料的發色團學說[28]，偶氮染料橙Ⅱ的發色基團是偶氮基，發色體是萘基偶氮苯，其助色基團為羥基(使顏色加深)和磺酸(給予染料水溶性以及對纖維蛋白的親和力)。橙Ⅱ染料溶液在紫外區230和310 nm處的吸收分別由苯基和萘基引發；而其在可見區484 nm處的特征吸收則是由分子結構中N=N的n-π*電子躍遷產生[29]。由圖1(a)可知，橙Ⅱ的礦化明顯滯后于其脫色，15 min時橙Ⅱ脫色率高達98.2%而其礦化率僅為37.3%。相應地，橙Ⅱ在脫色過程中，其發色基團N=N的降解速度快于苯基和萘基的降解速度(見圖1(b))。由于橙Ⅱ脫色是由N=N斷裂所致，該結果說明，雖然·OH對有機物的降解不具有選擇性[9]，但橙Ⅱ分子結構中與·OH反應最活躍的部位是N=N。

圖2(a)和(b)分別是橙Ⅱ脫色過程用準一級動力學方程全過程擬合和兩段擬合情況對比。

在高效降解有機污染物體系的研究中，分段擬合的方法近年來日益受到重視[9,20,30]。從催化過程的角度分析，由圖1(a)可見，由于聚合硅酸鐵催化活性極高，橙Ⅱ催化降解過程的快速降解段明顯掩蓋了其誘導段，使得橙Ⅱ脫色主要由快速降解段和慢速降解段組成。作者在前期的研究表明[31]，在·OH氧化過程中，橙Ⅱ的降解可以分為染料脫色(N=N裂解)、發色體降解(苯基和萘基氧化、開環生成小分子有機中間產物)、最終礦化(小分子有機中間產物礦化成二氧化碳和水)等過程。由此，在高效降解體系中，高濃度·OH會快速分解橙Ⅱ的發色體并產生小分子有機中間產物，使得體系中爭奪·OH的有機物種類短時間急劇增加，最終導致橙Ⅱ脫色演化成兩個階段進行[32]。根據圖2(b)的分析，橙Ⅱ的脫色以15 min為時間節點可以分為兩個階段：快速脫色段主要以N=N斷裂為主，發色體降解為輔；慢速脫色段主要以發色體降解和礦化為主，脫色為輔。對比圖2(a)和(b)可見，兩段擬合法的相關系數明顯高于全過程擬合法。以上結果說明，對于聚合硅酸鐵多相UV-Fenton體系中的橙Ⅱ脫色過程，用一級動力學方程對其脫色過程擬合時，兩段擬合法明顯優于全過程擬合法。

2.2 聚合硅酸鐵多相UV-Fenton體系中橙Ⅱ脫色動力學常數分析

在多相UV-Fenton體系中，H2O2的濃度將最終決定體系羥基自由基的極限濃度[26,33]，而催化劑用量將影響羥基自由基的生成速率[34-35]。因此，在聚合硅酸鐵多相UV-Fenton體系中，H2O2濃度和催化劑用量將最終決定體系中橙Ⅱ的脫色速率。圖3是H2O2濃度對橙Ⅱ脫色過程的影響，其中圖3(a)和(b)分別是準一級動力學方程全過程擬合和兩段擬合情況。圖4是催化劑用量對橙Ⅱ脫色過程的影響，其中圖4(a)和(b)分別是準一級動力學方程全過程擬合和兩段擬合情況。圖3和4擬合得到的動力學常數列于表1。

由表1可知，無論是全過程擬合還是二段擬合，其動力學常數均是隨H2O2的初始濃度增加而變大，表明在實驗范圍內，體系對橙Ⅱ的降解能力隨H2O2初始濃度增加而增強。由圖3(a)可以看出，用全過程擬合法時，隨H2O2的初始濃度增加，橙Ⅱ脫色實驗值與擬合線離散程度越大，對應于表1中k的相關性R2值從0.994降低到0.933。該結果說明，體系降解橙Ⅱ的能力越強，用全過程擬合法擬合的效果越差。由圖3(b)和表1可見，當用兩段擬合法時，無論是在快速脫色還是慢速脫色階段，橙Ⅱ脫色實驗值與擬合線重合程度均很高，兩段擬合法的準一級動力學常數相關性R2值良好。該結果說明，用二段擬合法進行準一級動力學方程擬合能更好地反映不同H2O2濃度對橙Ⅱ降解過程的影響。

相類似地，在實驗范圍內，當催化劑用量增加時，羥基自由基生成速率加快，體系降解能力增強，橙Ⅱ脫色實驗值與全過程擬合線離散程度越大，對應于表1中k的相關性R2值從0.983降低到0.948。而兩段擬合法則能很好地反映不同催化劑用量對橙Ⅱ降解過程的影響。在快速脫色和慢速脫色階段，橙Ⅱ脫色實驗值與兩段擬合線重合程度均優良(見圖4(b))。

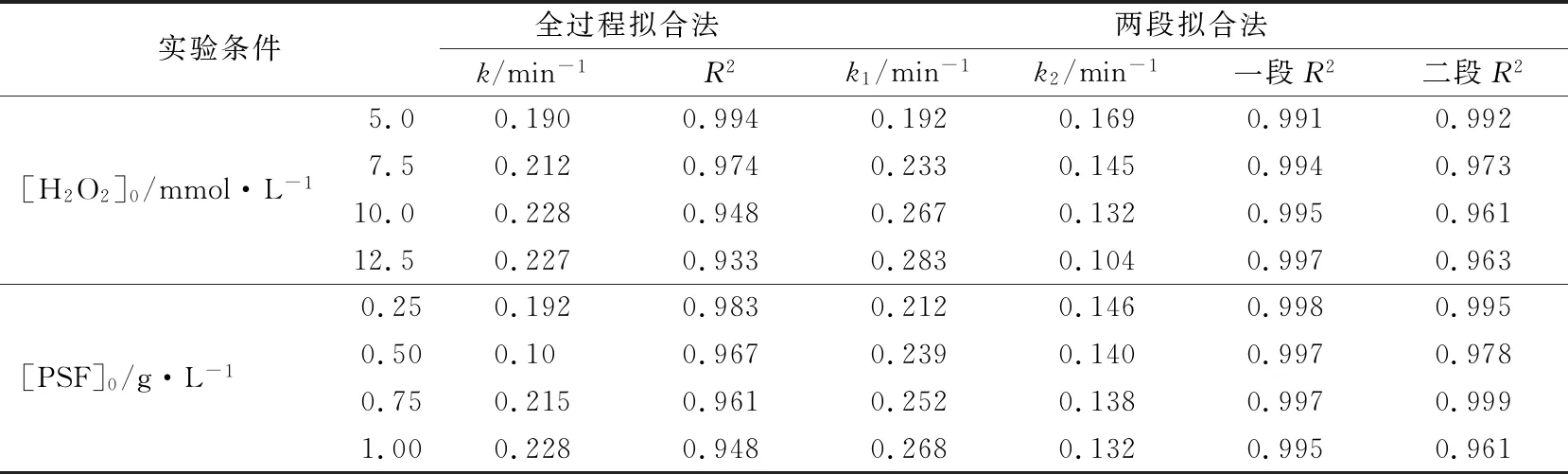
表1 不同反應條件下全過程擬合和兩段擬合動力學常數k及相關性R2

在多相高級氧化體系中，催化劑用量和H2O2濃度與有機污染物降解動力學常數之間能夠建立良好的數學模型。例如，陳美娟等在討論紫外/TiO2/芬頓復合工藝降解布洛芬的研究中發現[25]，布洛芬降解動力學常數的自然對數值(lnk)與[H2O2]0和ln[TiO2]0存在線性相關。對于聚合硅酸鐵多相UV-Fenton體系，數據分析發現，橙Ⅱ脫色動力學常數的自然對數值(lnk)與催化劑用量[PSF]0和H2O2初始濃度[H2O2]0之間可以直接建立良好的線性相關，其線性關系可以表述為：

lnk=a[PSF]0+b

(4)

lnk=a′[H2O2]0+b′

(5)

式中，a和a′為擬合直線的斜率，b和b′為擬合直線的截距。相關線性回歸情況見圖5和表2。

由圖5和表2結果可知，橙Ⅱ脫色過程中，全過程擬合的lnk和兩段擬合的lnk1和lnk2與[PSF]0和[H2O2]0呈現一定的線性關系，其中兩段擬合法精度更高。基于多元一次線性方程[36]，可以將催化劑用量[PSF]0和H2O2初始濃度[H2O2]0對橙Ⅱ脫色動力學常數的共同影響進行數學歸納，其關系式見式(6)～式(8)。

全過程擬合法：

lnk=m1[H2O2]0+m2[PSF]0+m

(6)

兩段擬合法：

lnk1=n1[H2O2]0+n2[PSF]0+n

(7)

lnk2=o1[H2O2]0+o2[PSF]0+o

(8)

式中，m1，m2，m和n1，n2，n和o1，o2，o分別為方程多元變量的參數。

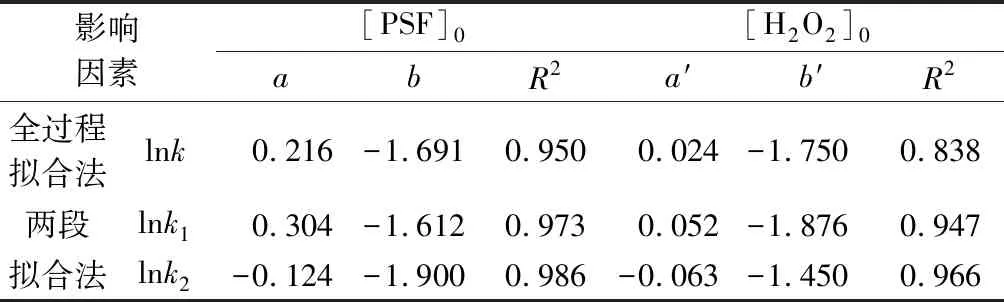
表2 lnk、lnk1和lnk2與[PSF]0和[H2O2]0的線性方程的參數值

根據表2中的數據，利用統計軟件IBMSpassStatistics進行多元線性回歸，可以計算得到式(6)～式(8)中的相關參數值，并最終得到以下方程：

全過程擬合法：

lnk=0.026[H2O2]0+0.175[PSF]0-1.934

(9)

兩段擬合法：

lnk1=0.053[H2O2]0+0.243[PSF]0-2.119

(10)

lnk2=-0.060[H2O2]0-0.192[PSF]0-1.264

(11)

由此，對于聚合硅酸鐵多相UV-Fenton體系，建立了H2O2初始濃度和催化劑用量與橙Ⅱ脫色動力學常數之間的具體數學關系。

2.3 聚合硅酸鐵多相UV-Fenton體系中橙Ⅱ脫色的動力學模型

對于聚合硅酸鐵多相UV-Fenton體系，根據全過程擬合法[37]，橙Ⅱ脫色的動力學模型用公式(3)表示(Ct=C0e-kt)。

相應地，根據兩段擬合法，橙Ⅱ脫色的動力學模型為[29-34]：

快速階段：

Ct=C0e-k1t(0≤t≤ta)

(12)

慢速階段：

Ct=C0e-k1tae-k2(t-ta)(ta≤t≤tb)

(13)

在兩段擬合模型中，橙Ⅱ的脫色包含快速階段和慢速階段兩個階段，其一級動力學常數分別為k1和k2。ta是兩個階段的分界時間點，為15 min，且橙Ⅱ完全脫色所需時間為30 min(tb)。

為比較全過程擬合動力學模型和兩段擬合動力學模型的精度，分別設計了橙Ⅱ快速、中速、慢速脫色條件的驗證實驗，其初始的實驗條件見表3。

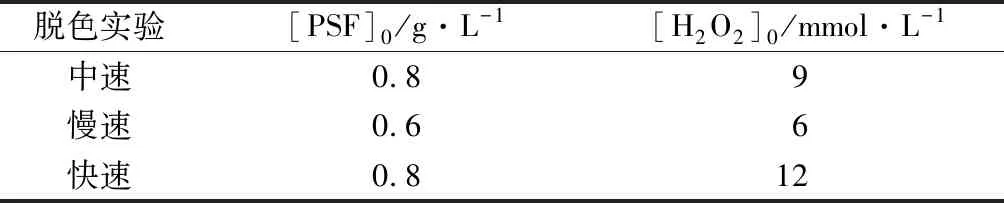
表3 驗證實驗的初始條件

驗證實驗值見圖6中的散點，根據全過程擬合和兩段擬合法得到的動力學常數實驗值列于表4。同時，根據表3中催化劑用量[PSF]0和H2O2初始濃度[H2O2]0，利用公式(9)～(11)可以計算得到全過程擬合和兩段擬合法動力學常數理論值，該值一并列于表4。

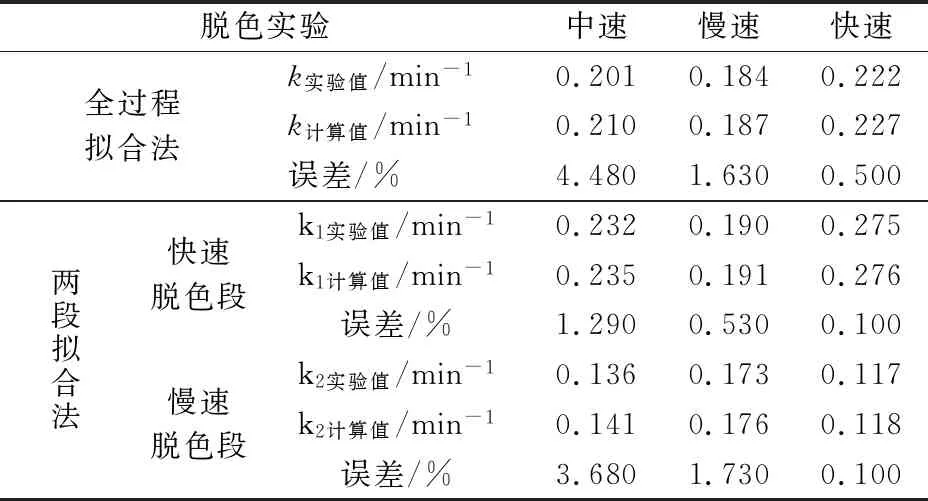
表4 全過程擬合和兩段擬合法橙Ⅱ脫色一級動力學常數理論值與實驗值的比較

根據表4中動力學常數理論值，由式(3)、式(12)和式(13)可以得到不同實驗條件下橙Ⅱ脫色的理論動力學模型，并且可以分別計算橙Ⅱ濃度隨時間變化的理論值，見圖6中的曲線。

圖6和表4的結果說明，在慢速降解條件下，橙Ⅱ脫色全過程擬合和兩段擬合動力學模型的理論值與實驗值吻合均較好。體現在圖6(a)和(b)中，實驗值(散點)與理論計算值(曲線)重合度均較高。該結果說明，兩種擬合模型均能有效地應用于橙Ⅱ慢速脫色的降解體系。反之，在快速降解條件下，橙Ⅱ脫色兩段擬合動力學模型明顯優于全過程擬合動力學模型，其理論值與實驗值吻合度更高。

3 結論

聚合硅酸鐵多相UV-Fenton體系中，橙Ⅱ的脫色以15 min為時間節點分為快速和慢速脫色兩個階段。快速脫色階段主要以N=N斷裂為主，發色體降解為輔；慢速脫色階段主要以發色體降解和礦化為主，脫色為輔。相對于全過程擬合法，橙Ⅱ脫色的兩段擬合法得到的動力學模型精度更高、誤差更小，能夠為橙Ⅱ的脫色過程提供更為精確的理論計算。