TBL理論下3C產品可持續閉環物流網絡模糊優化

霍晴晴，郭健全

上海理工大學 管理學院，上海200093

1 引言

電子類產品全球消費增加的趨勢及其本身壽命的縮短，使得廢棄電子設備的回收和處理問題日益受到關注[1]。2018 年，3C 產品（含通信產品、消費類電子產品）銷量占電子設備消費市場的59%，成為全球電子設備消費品市場的主要貢獻者[2]，回收和循環利用廢棄3C產品的問題亟待解決[3]。閉環物流是正向物流和逆向物流的集成，設計合理的閉環物流網絡可有效回收廢棄產品[4]。Miao等[5]通過分析收集點覆蓋面積對于回收率的影響，構建了第三方主導的閉環物流網絡模型；李曉靜等[6]從閉環供應鏈的角度出發，研究在不同的供應鏈結構下，制造商對于回收模式選擇的影響因素；盧榮花等[7]研究了零售商環境下閉環供應鏈回收渠道選擇的影響因素。以上研究尚未探討3C產品的閉環物流網絡模型設計，也未考慮閉環物流網絡的可持續性。

隨著社會對可持續發展的關注，建立可持續性閉環物流網絡是研究人員和實踐者面臨的一個重要問題[8]。嚴南南等[9]在低碳視角下兼顧成本最小化，對汽車產業逆向物流節點設施選址問題進行建模，并通過實證分析驗證了模型的有效性；Sushmita 等[10]將經濟成本、環境成本納入旨在通過區域合作實現可持續性的模式中，研究了印度制藥業的可持續性；Navid 等[11]考慮經濟和環境目標，研究了家電行業可持續性閉環物流網絡。TBL（三重底線理論）理論擴展了可持續的目標，該理論認為經濟責任、社會責任和環境責任是企業可持續發展中應當履行的基本責任，僅從經濟和環境保護角度思考是不夠的，有必要考慮社會影響[12-13]。Ioannis 等[14]根據TBL理論制定了衡量逆向物流社會責任績效的指標框架。Meyer 等[15]設計供應鏈時考慮社會維度，分析了阿根廷東北部地區林業實施可持續性閉環物流的可行性。以上研究尚未從整體上構建可持續性閉環物流網絡模型，且未考慮到閉環物流網絡中的不確定性。

閉環物流網絡中，處于逆向物流過程的產品數量往往是模糊的，考慮不確定因素能更好的解決現實問題。Kim 等[16]運用魯棒優化建立了服裝行業的閉環供應鏈模型，研究了產品回收量和客戶需求的不確定性；Yu等[17]運用隨機規劃解決了回收量和再制造價格不確定條件下的雙目標混合整數規劃問題；魯棒優化采用事先制定情景數的方法，雖然具有一定的穩定性但降低了模型的適用性[18]；隨機規劃需要足夠的歷史數據估計不確定參數的精確分布情況，對企業實際運作挑戰較大[19]。

模糊規劃因其能更好的處理主觀與客觀共存的非精確數據而被廣泛應用[20-21]。Mohanty 等[22]提出了一種模糊決策分析模型，并運用模糊優化方法求解以加強不確定環境下綜合物流的可持續性。Djordjevic等[23]建立汽車行業模糊優化模型，利用模糊規劃解決客戶需求的不確定性。當前研究尚未考慮模糊優化在3C產品閉環物流網絡中的應用，且未統籌閉環物流網絡的最佳設施選址和最優車輛運輸路徑優化。

綜上所述，本文根據TBL 理論分別以經濟成本最小、環境影響最小、社會效益最大為目標函數，建立了3C產品可持續閉環物流網絡模型。經濟成本包含固定建設成本，運營成本和運輸成本；環境影響包含碳排放及水和土壤污染；社會效益包含創造的工作崗位數量與為員工提供的技能培訓時長。考慮到3C產品回收量的不確定性，將回收量看成三角模糊數，利用模糊機會約束規劃方法實現約束條件清晰化。以上海市3C產品閉環物流網絡為例，通過GA分別進行單目標與模糊多目標求解，在此基礎上，規劃出最佳設施選址和最優車輛運輸路徑。通過對比分析計算結果，驗證了模型的有效性。以上文獻與本文的對比情況如表1所示。

表1 文獻總結

2 3C產品可持續閉環物流網絡模型

2.1 3C產品閉環物流網絡結構

3C產品閉環物流網絡結構如圖1所示，主要由供應商、工廠、零售點、顧客、分拆檢測中心、再制造中心、處理中心7部分組成。

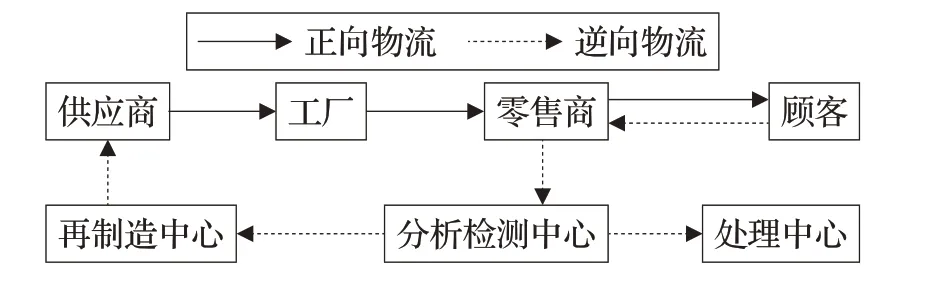
圖1 3C產品閉環物流網絡結構

在正向物流中，供應商將零部件配送至工廠，工廠將零部件制成產品運送至零售點，顧客至零售點處購買3C產品。

在逆向物流中，顧客將廢舊3C 產品送至零售點處統一收集，零售點將收集的一定數量的廢舊3C 產品運往分拆檢測中心；分拆檢測中心根據檢測情況，將無使用價值的部分運往處理中心集中處理，有重復使用價值的零部件分拆后運往再制造中心；再制造中心將翻新的零部件運往供應商實現循環使用。

2.2 模糊多目標模型

2.2.1 模型假設

（1）工廠、分拆檢測中心、再制造中心分為高、低兩種技術類型，分別以1、2來表示。

（2）供應商、工廠、零售點、分拆檢測中心、再制造中心、處理中心的候選位置與數量已知。

（3）各節點之間的運輸成本與運輸距離和運輸量成正比。

（4）顧客在零售點購買新產品，與此同時，將廢舊3C產品送往就近零售點處回收。

（5）節點之間的距離并非兩點間直線距離，而是貨車行駛距離。

（6）CO2排放量與貨車運輸距離和運輸量成正比。

（7）水污染、土壤污染與處理不當的量成正比。

2.2.2 符號

2.2.3 參數

2.2.4 決策變量

Yl為0-1 變量，若選擇候選工廠，則Yl=1，否則為0；Yr為0-1 變量，若選擇候選零售點，則Yr=1，否則為0；Yd為0-1變量，若選擇候選分拆檢測中心，則Yd=1，否則為0；Ym為0-1 變量，若選擇候選再制造中心，則Ym=1，否則為0；為0-1 變量，若車輛V 在第k 條路線運輸，則=1，否則為0；，，，，，為0-1變量，若車輛在兩節點運輸時選擇第K條路線Y為1，否則為0。

2.2.5 數學模型的建立

式（1）表示3C產品閉環物流網絡的總經濟成本，包括網點建設成本、運營成本及物流過程中的運輸成本。

式（2）表示3C產品閉環物流網絡的環境影響，環境目標的設定考慮到了閉環物流網絡運輸過程中產生的CO2排放量[24]，以及收集產品的正面環境影響。CO2排放水平根據車輛行駛路程與運載量確定，正面影響主要包括因回收而避免的不當處理所可能產生的水污染、土壤污染。

式（3）表示3C產品閉環物流網絡產生的社會效益。Arampantzi等[25]將社會因素分為五類：需求滿意、資源公平、就業機會、區域發展，以及該地點的安全級別和醫療設施準入級別。由于電子廢棄物回收量的多變性在某一時期可能導致裁員，對企業和政府來說，保持一定的勞動力水平是很重要的。政府不希望勞動力水平下降，企業不希望因裁員而支付補償[26]，因此本文將為員工提供的工作機會與通過培訓提高員工技能作為社會目標的指標。

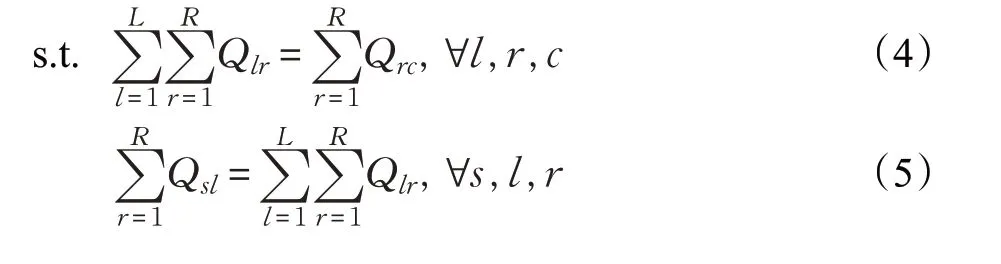
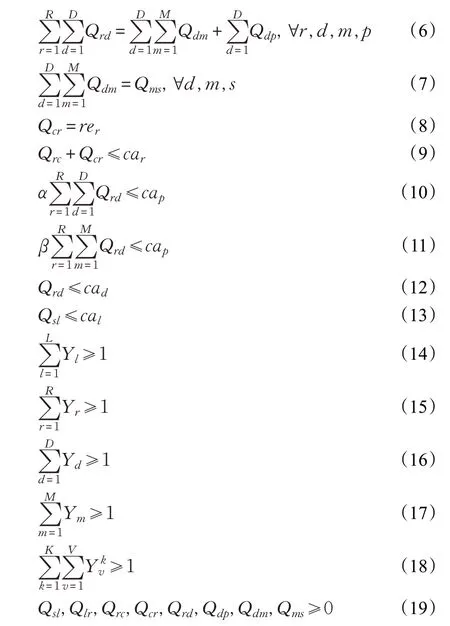
式（4）～（8）表示流量均衡約束，式（9）～（13）表示容量約束，式（14）～（17）表示至少選擇一個工廠、零售點、分拆檢測中心、再制造中心，式（18）表示至少有一輛車完成整個物流網絡的運輸，式（19）表示運輸量非負。

3 模型求解

3.1 模糊機會約束清晰化

3C產品閉環物流網絡中回收量rer為模糊參數，因此本文求解的不再是約束條件清晰的規劃問題。對于類似的物流網絡模糊規劃問題，宜采用模糊機會約束規劃方法[27]。首先將回收量看作三角模糊參數，其次應保證約束條件成立概率控制在決策者制定的置信水平之上，通過對模糊對應式進行等價變換，使模型的約束條件轉化為等價的清晰約束[28]。

綜上所述，在整個施工項目的施工過程中進行相應的現場施工管理具有重要意義。對于市政工程企業的穩定，長期，高效發展來說，有必要加強對施工技術的管理。因此，提高建設項目的施工質量和確保項目按時完成，鼓勵市政工程公司取得更多的經濟效益，必須實現“經濟，社會和環境”的和諧統一發展。

將rer看作三角模糊數，記rer=(rer1,rer2,rer3)其中rer1,rer3分別為3C 產品企業給定的置信區間上下界，rer2為最可能值。其模糊隸屬函數如下表示：

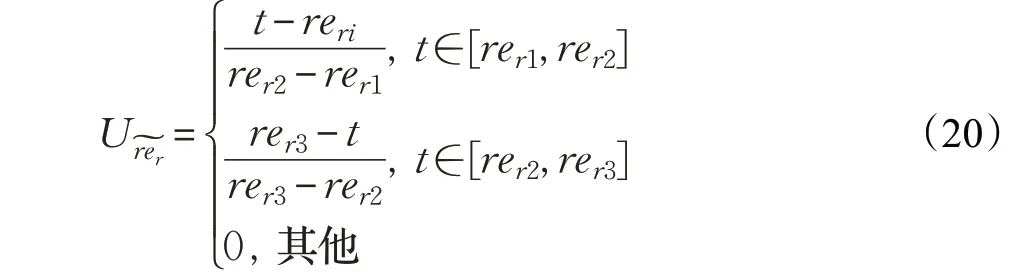
根據FCCP（模糊機會約束規劃）的清晰化定義[29]，可以推導出以下引理：

設三角模糊數r 為(r,r,r)，則對任意給定的置信水

3.2 多目標的模糊化處理

在多目標優化問題中，多目標最優解應該包含各子目標的貢獻，然而子目標間往往存在沖突，由于模糊多目標規劃能針對多個相互沖突的目標提供多種決策方案且具有靈活性而被廣泛應用[30]。各子目標最優解與多目標最優解之間的相互關系是模糊的，隸屬度函數可以對模型中的多個子優化目標分別進行模糊化處理[31]。選擇合適的隸屬度函數是子優化目標模糊化的前提[32]，參照文獻[33]的做法，選擇如下隸屬度函數，令gv表示一類越大越優型目標函數，gs表示一類越小越優型目標函數，則隸屬函數可表示為：

式中，μg(x)表示E 的隸屬度函數，μ(0 ≤μ ≤1)的大小反映了優化結果的滿意度，λ 和γ 分別表示形狀系數，gvmin、gvmax和gsmin、gsmax分別表示gv和gs的最小值、最大值，λ,γ＞0 且不為1。引入變量ζ ，將原目標函數轉化為約束條件，即 μg(x)≥ξ(0 ≤ζ ≤1)，則此時模型可轉化為maxξ的單目標函數。根據上述原理，本研究所構建的多目標模型可表示為：maxξ。

此時約束條件除包括式（4）～（19），還包括：

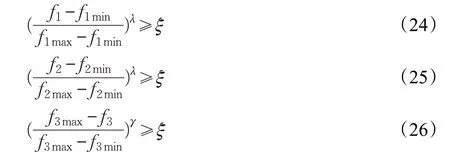
求解思路為：先求出各子目標在所有約束條件下的最優解，再利用這些最優解將各子目標函數模糊化（即確定隸屬度函數），然后使交集的隸屬度函數取最大值，該解即為多目標問題的最優解。

3.3 基于遺傳算法的模型求解

遺傳算法（GA）是基于遺傳學機理和達爾文自然選擇理論的元啟發式優化技術，適用于搜索近似最優解，被廣泛應用于復雜系統的優化問題求解[32]，本文擬采用GA來求解3C產品閉環物流網絡的模糊多目標模型，從而規劃多目標決策，具體說明如下所示。

（1）染色體編碼與初始化：本文的染色體數組表示設施L,D,P,M,R是否建立，車輛V是否在路線K上運輸，路線k上節點是否被選擇，節點間的3C產品運輸量。在GA 求解的過程中，自動確定設施是否開放，設備類型以及規劃相應路線。

（2）適應度評估與選擇：染色體的適應度反映了被選擇概率。在滿足約束條件的情況下，利用目標函數（1）、（2）、（3）計算各個個體的適應度值。適應度值可直觀反映個體的優劣。選擇操作避免遺漏，提高全局收斂性，采用輪盤賭策略進行選擇。通過評估適應度值，選出適應度大的個體作為父代，提高全局收斂性。

（3）交叉與變異：交叉使子代同時繼承父母代的基因，保持更高的適應性。變異使某個基因以一定的概率隨機發生突變。交叉和變異不僅產生新個體，而且提高種群局部搜索能力。

（4）終止條件：若達到預先設定的最大進化代數，終止算法；否則轉向步驟（2）。

4 算例

4.1 數據來源

本文以上海市3C 產品為研究對象，零售點選址以廢棄3C產品回收需求出發，選取3個零售點，坐標為r1、r2、r3；候選的工廠分別編號為l1、l2；候選的分拆檢測中心編號為d1、d2；候選的再制造中心編號為m1、m2；廢物處理廠編號為p。模型中被選點以及候選點位置分布如圖2 所示，各個節點間的距離由谷歌地圖測量而得，具體數值如表2 所示。本文通過調研，整理得出廢舊3C 產品回收量的模糊值，如表3 所示。其他參數數值見表4。

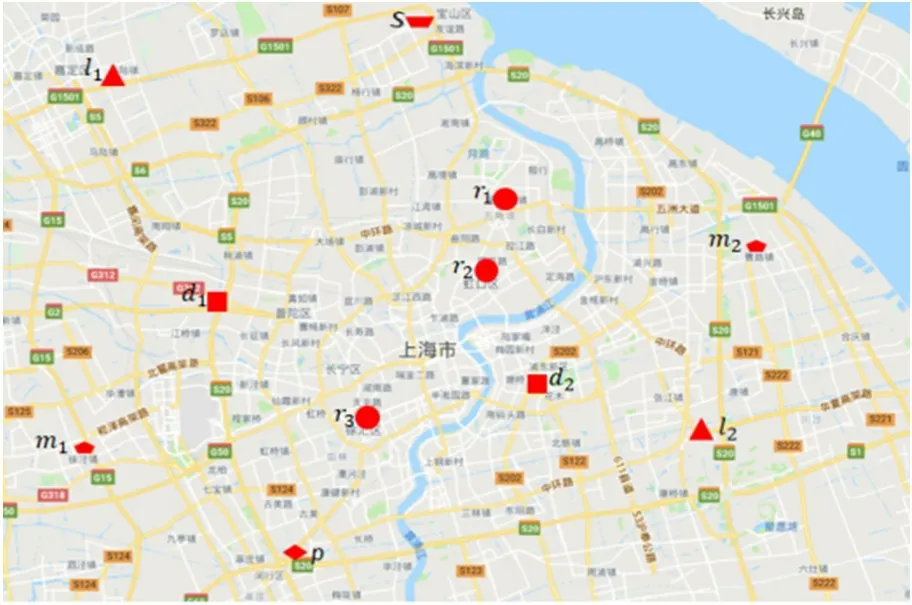
圖2 被選點與候選點的位置分布圖

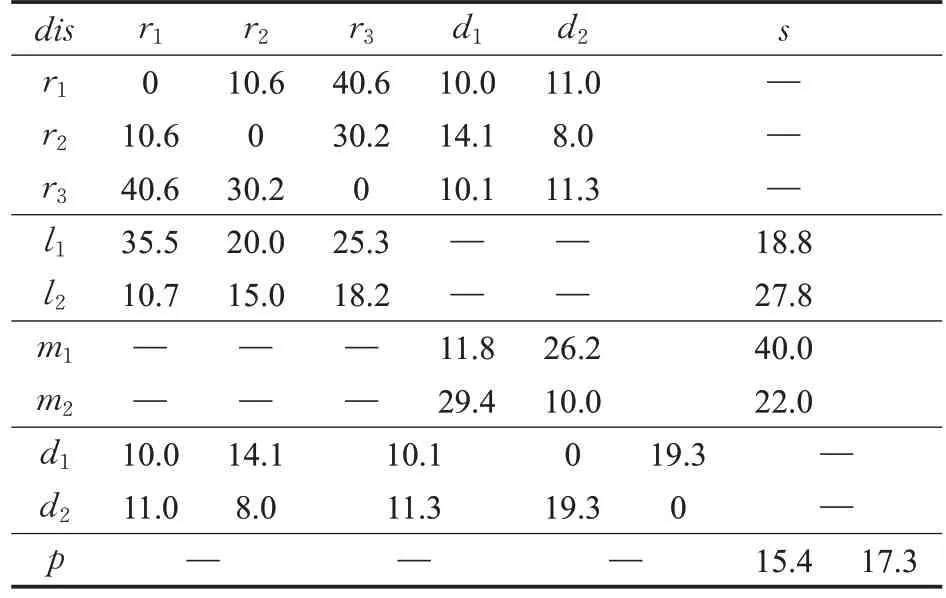
表2 各相關節點間的距離 km

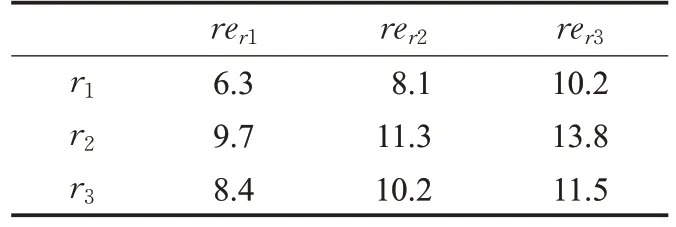
表3 零售點回收量的三角模糊數t

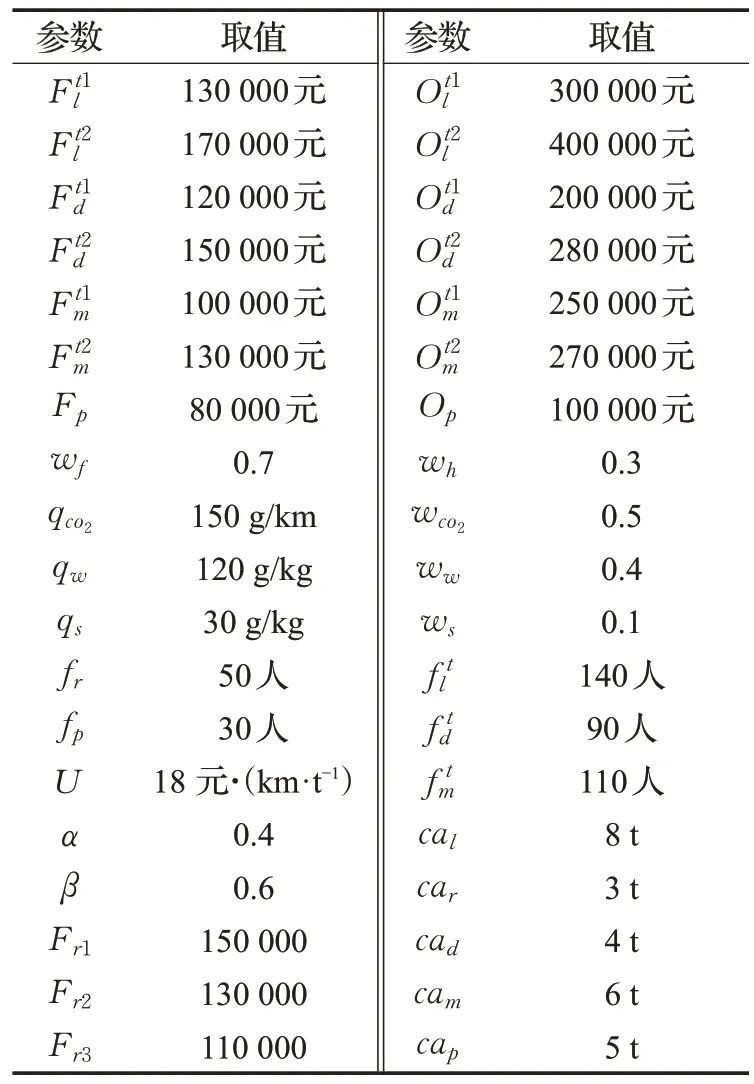
表4 其他相關參數數據

4.2 算例結果分析

為對模型子優化目標進行模糊化，首先需確定3C產品閉環物流網絡的最小經濟成本，最小環境影響，最大社會效益，即在僅考慮各子優化目標的情況下采用GA對模型求解，結果如圖3和表5所示。

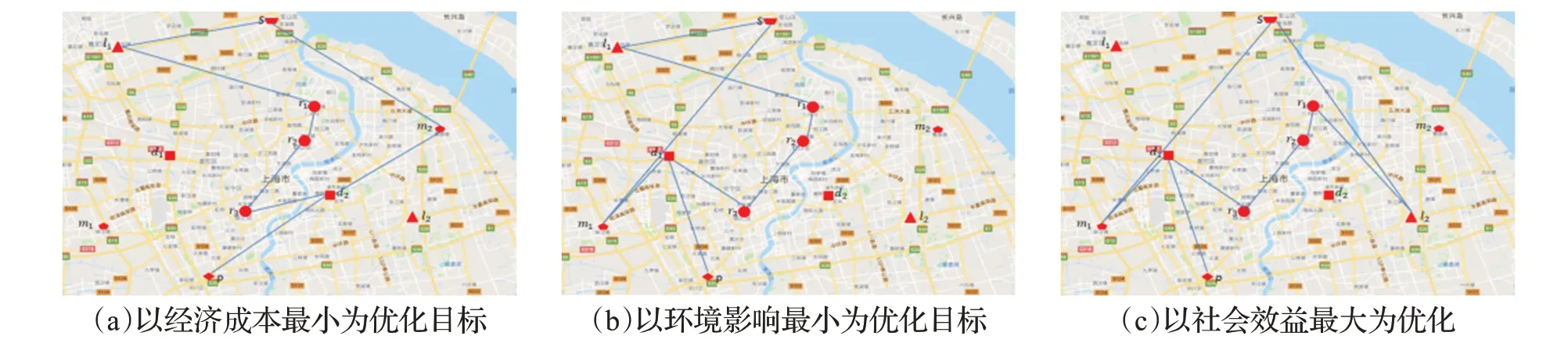
圖3 單目標優化結果

表5 僅考慮各子目標時的優化結果

從圖3 與表5 給出的結果可看出，若在規劃中僅考慮3C 產品閉環物流網絡的經濟成本最小，則傾向于選擇技術類型較低的設施點，此時經濟成本達到理論上的最小值，為1 895 958元，然而此時閉環物流網絡的環境影響將偏大，達到1 649；若僅考慮3C 產品閉環物流網絡的環境影響最小，則傾向于選擇開放距離較近的設施點，此時環境影響達到理論上的最小值，即1 237，然而此時社會效益顯著下降，僅為223；若僅考慮3C 產品閉環物流網絡的社會效益最大，則傾向于選擇技術類型較高的設備點，此時社會效益達到理論最大值328，然而經濟成本顯著上升，達到2 673 850 元。因此規劃模型的三個子優化目標在一定程度上互相沖突，很難同時達到最優。

在上述優化結果的基礎上，可依據式（24）～（26）將優化模型中的子優化目標分別進行模糊化，并在此基礎上將原始多目標問題轉化為基于最大滿意度的單目標優化問題。接著，采用GA對該單目標優化問題進行求解，優化中，各進化代數最優規劃方案的滿意度如圖4所示，最終優化結果如圖5和表6、7所示。

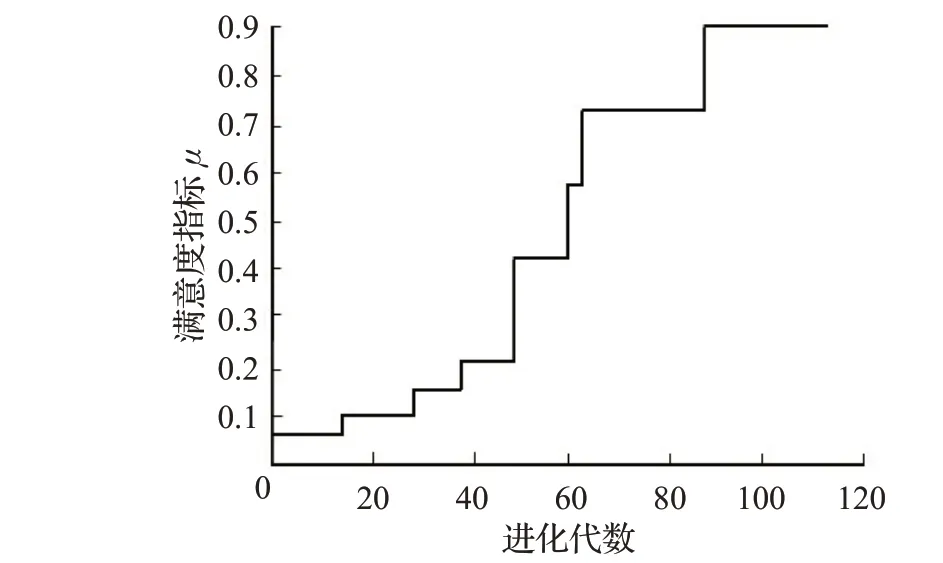
圖4 算法收斂性

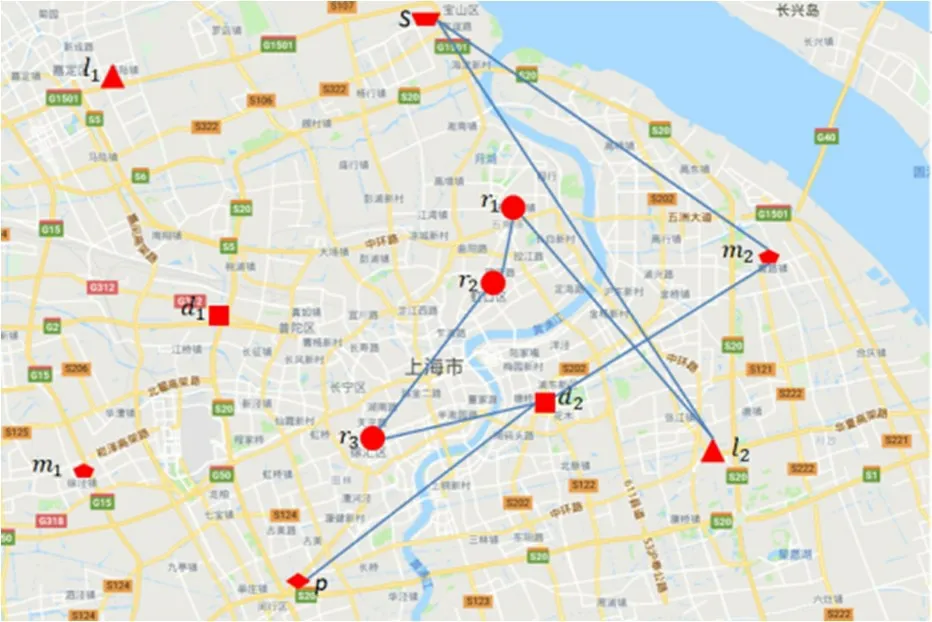
圖5 模糊多目標優化結果

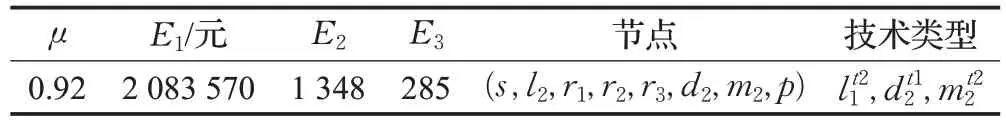
表6 最大滿意度時的優化結果

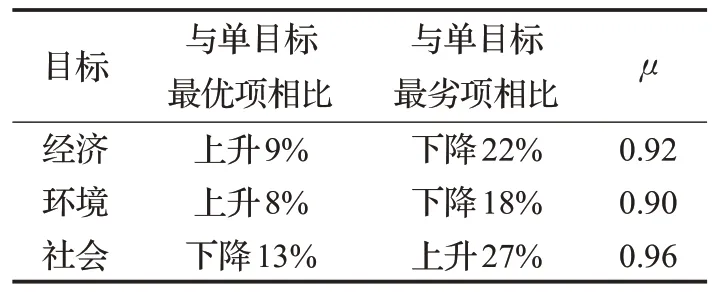
表7 模糊優化與單目標優化結果對比圖

由表6與表7可看出，在同時優化三個子目標時，各子目標與單目標優化相比均做出一定讓步，但是與單目標優化的最劣項相比經濟目標下降22%，環境目標下降18%，社會目標上升27%，三個子目標優化的滿意度分別為0.92、0.90、0.96，均不低于0.90，且整體優化的滿意度達到最大值0.92。

5 總結與展望

本文以不確定條件下3C產品閉環物流網絡可持續性為背景，基于TBL理論，以經濟成本最小化，環境影響最小化，社會效益最大化為出發點，建立了3C產品閉環物流網絡模糊多目標優化模型，規劃出最佳設施選址和最優車輛運輸路徑。分別采用三角模糊函數和模糊優化處理不確定性及多目標沖突，在此基礎上建立了基于最大滿意度的單目標優化模型，并采用遺傳算法求解。算例結果證明了本文所建模型及求解算法的有效性。

本文在以往研究的基礎上考慮了3C產品回收量的不確定性以及社會效益，使得模型更符合現實意義。但是3C 產品閉環物流網絡具有多種不確定性，下一步還可考慮回收質量、再制造價格等方面，且處理多目標的方法也是多樣的，可以考慮多種處理方法（如ε約束法）的優化。