一類競爭的病菌傳染模型在一定條件下的穩定性研究

◎左曉虹

（三門峽職業技術學院公共教學部，河南三門峽472000）

2020 年新型冠狀病毒肺炎疫情發生以來，中國政府采取積極的防控策略和措施，經過兩個多月的不懈努力，有效控制了新發病例的增長，本地傳播已經完全控制，但全球疫情卻不容樂觀，本次新冠病毒肺炎疫情暴發讓筆者再次深刻體會到傳染病的巨大威力，所體現出來的人與人、人與動物、動物與動物之間的關系及其疾病關系是立體的也是復雜的，黃永鵬教授強調要正視人與動物共病關系防范惡性疫病傳播，他指出人與動物交錯生活在一個共病的體系中，多數疾病人與動物的致病概率是一樣的。世界衛生組織根據近年的統計資料提出，在已知的能感染人的病原中有一半以上能在人與動物之間互相傳染。近30 年來新發現的傳染病達40 余種，幾乎每年都有一兩種新發傳染病。新發現的或重新出現的傳染病中80%是人與動物共患病[1]。

1 研究現狀及模型的建立

用數學建模思想描述傳染病在不同種群之間的關系，并用數學方法進行研究，用具體數字刻畫傳染病傳染規律，使得不同種群、相同種群之間的傳染得到合理的解釋和控制，用數學方法研究傳染病的規律，實現對傳染病的預防與控制，比如通過對新冠肺炎疫情全球大流行現狀分析[2]，對新冠肺炎COVID-19 疫情傳染機理和統計數據研究，擬合疫情變化趨勢圖,建立有控制的SIR 傳染模型[3]，為科學有效的傳染病疫情防控提供參考。為此筆者在文獻4 的基礎上進一步研究了一類競爭的病菌傳染模型

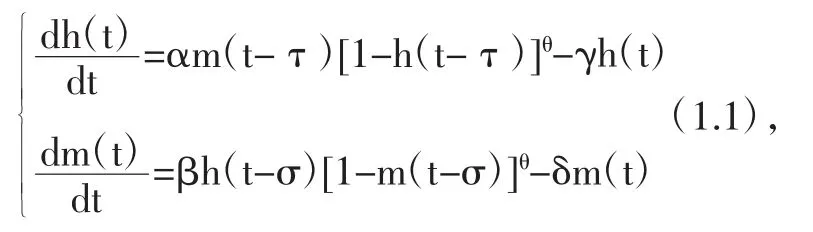
探討當τ，σ 充分小時模型正平衡態的穩定性，得出具體結論并帶入具體數據進行驗證。

文獻4 是以Lotka 和Volterra 提出的Lotka-Volterra 模型[5]為基礎建立了一類競爭的生態模型[4]。

（α,β,γ 均為實數，且 α＞0,β＞0,γ≥0,δ≥0,θ為正奇數）

并進行了初步探討，各參數的生態意義分別為：α 表示種群乙被帶有病菌的種群甲感染病菌的比率，β 表示種群甲被帶有病菌的種群乙感染病菌的比率，γ 表示種群甲的康復率，δ 表示種群乙的康復率，αm（t-τ）表示種群甲的抗病菌率，βh（t-σ）表示種群乙的抗病菌率，θ 為外界對種群的干擾參數。

模型（1.2）滿足如下初始條件：

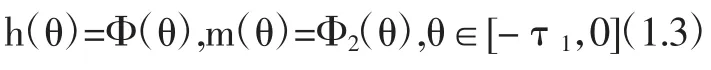
其中 τ1=max ｛τ, ｝σ ，Φi（i=1,2）非負且在[-τ1，0]上連續有界，h(o)=Φ1(0)＞0，m(o)=Φ2(0)＞0.

在文獻4 的基礎上筆者就一類競爭的病菌傳染模型（1.2）討論其當T，σ 充分小時模型正平衡態穩定性，給模型(1.2)各參數賦值，并運用Matlab 繪出相應的數值解圖形，對所得結論進行了驗證。

2 當τ，σ 充分小時模型正平衡態穩定性

設 h（t）=X（t）+h*，m（t）=Y（t）+m*，則模型（1.2）有線性近似系統為：

假設模型（1.2）中 τ=σ 且充分小，即 α=β，

γ=δ，則在很小的一個時間間隔里[t-b,t]，有

代入系統（1.2），則系統（1.2）的近似系統為：

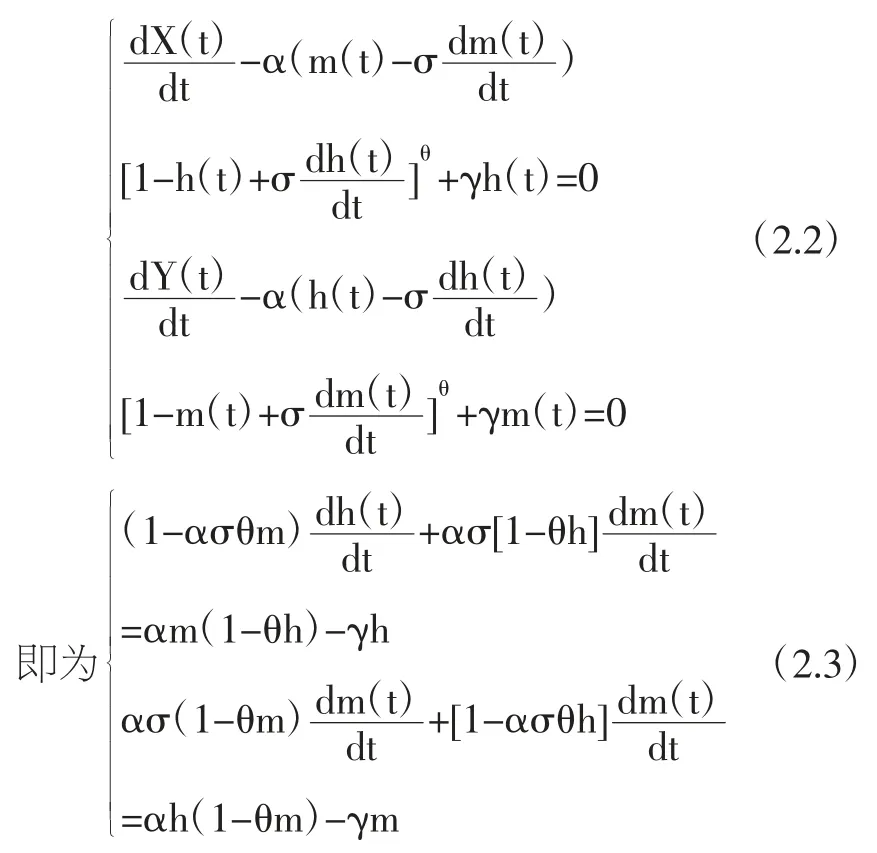
整理可得

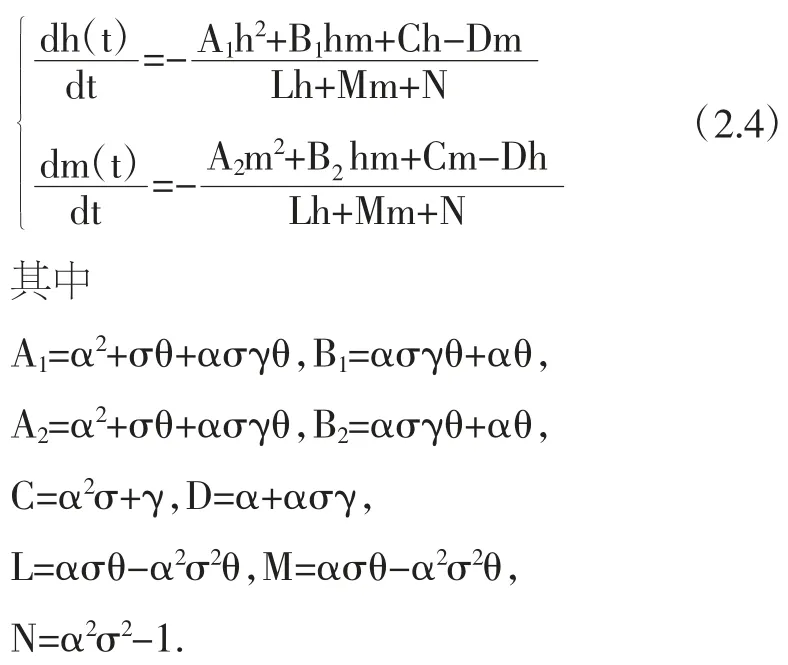
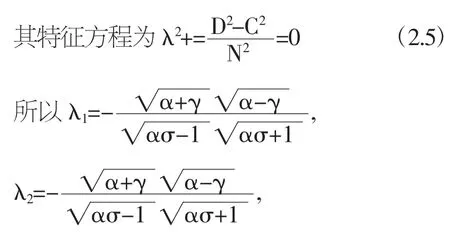
則當 α＞γ，且 ασ＞1 時，系統（2.5）有虛根.

綜上討論便有如下結論：

定理 對于模型

（1）當 α＞γ 且 ασ＜1 時，其平衡態（h*，m*）為中心且穩定；

（2）當 α＞γ 且 ασ＞1 時，其平衡態為鞍點且不穩定.

3 實例分析

對于系統

的正平衡態，現由定理1 則可以得出（3.1）的如下結論：

（1）若取τ=σ=0.5，此時該模型的正平衡態是穩定的（如圖3-1）。

（2）若取τ=σ=2.5，此時該模型的正平衡態是漸進穩定的（如圖3-2）。

（3）若取]τ=σ=4，此時該模型的正平衡態是不穩定的（如圖3-3）。

運用Matlab 繪出相應的數值解圖形，由圖形再次驗證定理1 的正確性.

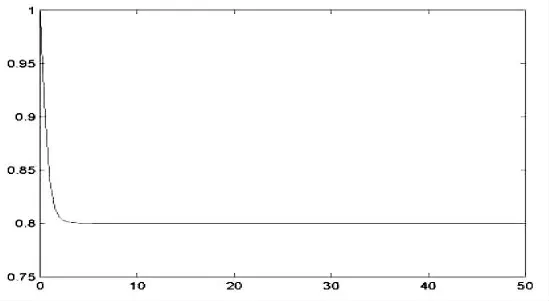
圖1 τ=σ=0.5 時的曲線擬合圖

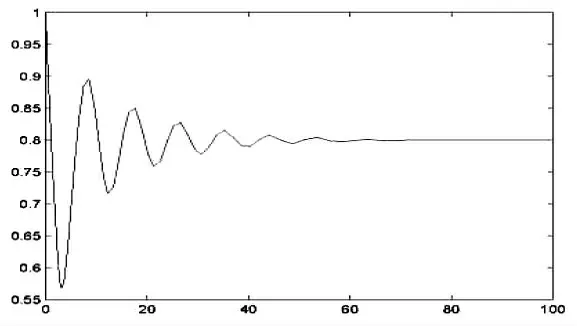
圖2 τ=σ=2.5 時的曲線擬合圖

圖3 τ=σ=4 時的曲線擬合圖