基于多元統計分析的黃河山東段水質評價研究

時文博 曹春燕 宋穎 李永軍 董方慧

摘?要：以黃河山東段為例，在利用方差分析（ANOVA）對高村、孫口、艾山、濼口和利津5個斷面2015—2017年各水質監測指標月度監測值進行時空尺度顯著差異性分析的基礎上，采用層次聚類分析法將180個水質樣本分成12組，并以各組樣本均值為基礎，運用綜合水質標識指數法對河流綜合水質進行評價。結果表明：黃河山東段綜合水質狀況良好，綜合水質類別為Ⅰ類或Ⅱ類;時間上，2015—2017年綜合水質狀況逐漸好轉;空間上，利津斷面綜合水質狀況最差，其余斷面從上游到下游綜合水質狀況呈好轉趨勢。

關鍵詞：水質評價;方差分析;聚類分析;綜合水質標識指數;黃河山東段

中圖分類號：TV882.1;X824?文獻標志碼：A

doi：10.3969/j.issn.1000-1379.2020.02.010

Abstract：The Shandong reach of the Yellow River was measured as the research area in this study. Based on the results of analyzing the temporal and spatial differences of monthly surveillance data of five monitoring sites from 2015 to 2017 according to the analysis of variance （ANOVA）， 180 samples were divided into 12 groups by hierarchical cluster analysis. Using the sample mean of each group as the input， the comprehensive water quality identification index of each group was calculated. The results show that the comprehensive water quality of the Shandong reach of the Yellow River is in good condition and the comprehensive water quality of the sampling sections is at class I to class Ⅱ levels. The comprehensive water quality condition has an upwarding trend from 2015 to 2017. The comprehensive water quality of Lijin section is the worst among five monitoring sites and from upstream to downstream， the comprehensive water quality has an upwarding trend except Lijin section.

Key words： water quality assessment; analysis of variance; cluster analysis; comprehensive water quality identification index; Shandong reach of the Yellow River

河流綜合水質評價是合理開發利用水資源及水環境管理的重要基礎工作，對水質監測數據進行合理評價能夠了解和掌握水體的污染程度，從而為水資源保護和水環境管理提供科學依據。由于水體環境的復雜性，因此評價方法的選擇是河流綜合水質評價的核心。水質評價方法大致可分為水質指數法和不確定性評價方法兩大類，目前應用較多的評價方法有水質指數法[1-5]、模糊綜合評價法[6-7]、灰色系統理論評價法[8-9]和人工神經網絡法[10-11]等不確定性評價方法。此外，近年來，物元分析[12-13]、可拓評價[14-15]、投影尋蹤技術（PP）[16-17]、集對分析[18-19]、TOPSIS法（即逼近理想解的排序方法）[20-21]、多目標決策-理想區間法（MODMIIM）[22]等新型不確定性研究方法和技術開始應用于河流水質綜合評價中。水質指數法具有計算方法簡單、物理概念清晰等優點，但是水質指數法通過有目的地選擇一些重要的水質指標，將復雜的水質監測數據轉換成可以理解和使用的信息，具有主觀性。不確定性評價方法充分考慮了水環境系統的隨機性、模糊性和灰色性[23]，能夠客觀反映水環境質量，但這些方法均需構造相應函數，存在計算過程復雜的缺點，且有的方法在使用過程中需要依靠經驗，有的方法存在分辨率低及計算時缺失信息多的缺點，有的方法不能準確判斷水質類別[24]，有的方法受人為因素干擾數據波動較大且沒有典型的分布規律[25]，這些不足限制了這些方法在實際應用中的推廣。上述水質評價方法為水環境管理和水資源規劃提供了決策支持，但在評價過程中通常將各時期、各斷面進行獨立評價，未考慮各種水體污染物在時間和空間上的差異性和相關性，導致了大量重復計算及評價過程的繁雜性。

當前水質評價方法應解決的主要問題是，充分利用大量水質監測數據的相似性與差異性，從而達到降維、簡化計算過程和提高分析結果可靠性的目的。為克服傳統評價方法在應對大量復雜樣本時難以解釋數據之間關聯性及差異性的缺點，在以往多元統計分析方法（如因子分析[26-27]、主成分分析[28]、方差分析[29]、聚類分析[30]）及綜合水質標識指數法[3]的基礎上，提出了基于多元統計分析和綜合水質標識指數的水質評價方法，并將其應用于黃河山東段水質評價中。該方法有以下顯著特點：簡化了計算過程，減少了水質評價的工作量;充分挖掘了水質監測數據的時空特征，特別適用于多斷面、長時間的水質評價;不僅可以定性評價，而且可以定量評價。

1?水質評價方法

1.1?基于多元統計分析和綜合水質標識指數的水質評價方法

該方法以多元統計分析和綜合水質標識指數法為理論基礎，其基本步驟如下。

（1）通過方差分析（ANOVA）對各斷面多年水質監測數據進行空間和時間尺度上的顯著性差異分析，識別出具有顯著差異的樣本。

（2）通過層次聚類分析（HCA）對樣本進行聚類分組。

（3）以各組水質數據為基礎，采用綜合水質標識指數法對水質狀況進行評價。

（4）將評價結果分解到各組對應的樣本點，從而實現多斷面、長時間大量樣本的水質評價。

1.2?方差分析

方差分析（ANOVA）是用于推斷兩個及兩個以上樣本的總體均值是否存在差異的顯著性檢驗，其基本思想是，通過分析不同來源的變異對總變異的貢獻程度，確定可控因素對研究結果影響的大小。數據的變異量可分解為組間變異和組內變異，組間變異即由可控因素引起的變異，組內變異即由隨機誤差引起的變異。根據控制變量個數不同，ANOVA可分為單因素方差分析和多因素方差分析。在本研究中，可控因素為時間或斷面，屬于單因素方差分析，計算公式為

1.3?層次聚類分析

聚類分析（CA）是一種統計分析技術，它是研究“物以類聚”的一種方法，其中使用最多的是層次聚類法。層次聚類分析法（HCA）的基本思想是，通過研究觀察對象之間的親疏程度，逐步將相似的對象聚合在一起，直至聚為一類。親疏程度的計算包括2類：樣本間距離和小類間距離，樣本間距離的測量方法有歐氏距離、歐氏距離平方、Cityblock距離（布洛克距離）和Mahal距離（馬氏距離）等，小類間距離的測量方法有最短距離法、最長距離法、中間距離法、重心法和離差平方和法（Ward法）等。本研究采用SPSS 19.0軟件實現聚類分析，樣本間距離和小類間距離分別采用歐式距離平方和Ward法測量。

1.4?水質標識指數評價法

（1）單因子水質標識指數。單因子水質標識指數可以完整地表示水質類別及與水功能區目標的比較情況，既可以對水質類別進行定性評價，又可以在同一類別中定量比較水質優劣。單因子水質標識指數pi由一位整數和小數點后兩位有效數字組成，其結構為pi=X1.X2X3，其中X1、X2、X3代表的含義及其數值確定見文獻[1]。

（2）綜合水質標識指數。綜合水質標識指數是在單因子水質標識指數的基礎上建立起來的，是一種河流綜合水質評價方法，該方法克服了單因子評價法以偏概全的缺點，能夠對河流綜合水質做出合理評價。其結構為Iwq=X1.X2X3X4，其中X1、X2、X3、X4代表的含義、X1.X2的計算公式及X3和X4的數值確定見文獻[3]。

根據綜合水質標識指數Iwq中的X1.X2可判定河流綜合水質級別，當1.0≤X1.X2≤2.0時，綜合水質類別為Ⅰ類;當2.07.0時，綜合水質類別為劣Ⅴ類且黑臭。

2?實例研究

2.1?研究區域概況及采樣點布設

黃河自菏澤市東明縣進入山東省，自西南向東北橫跨山東省西北部，黃河下游山東段干流河道全長628 km，流域面積1.83萬km2。山東沿黃城市主要有菏澤、濟寧、泰安、聊城、濟南、德州、濱州、淄博和東營。黃河作為山東省最主要的客水資源，其水資源質量優劣和多少對沿黃各市社會經濟的可持續發展具有舉足輕重的地位，因此水質狀況受到廣泛關注。在黃河山東段干流設置高村（S1）、孫口（S2）、艾山（S3）、濼口（S4）和利津（S5）5個斷面進行水質評價。

2.2?數據采集

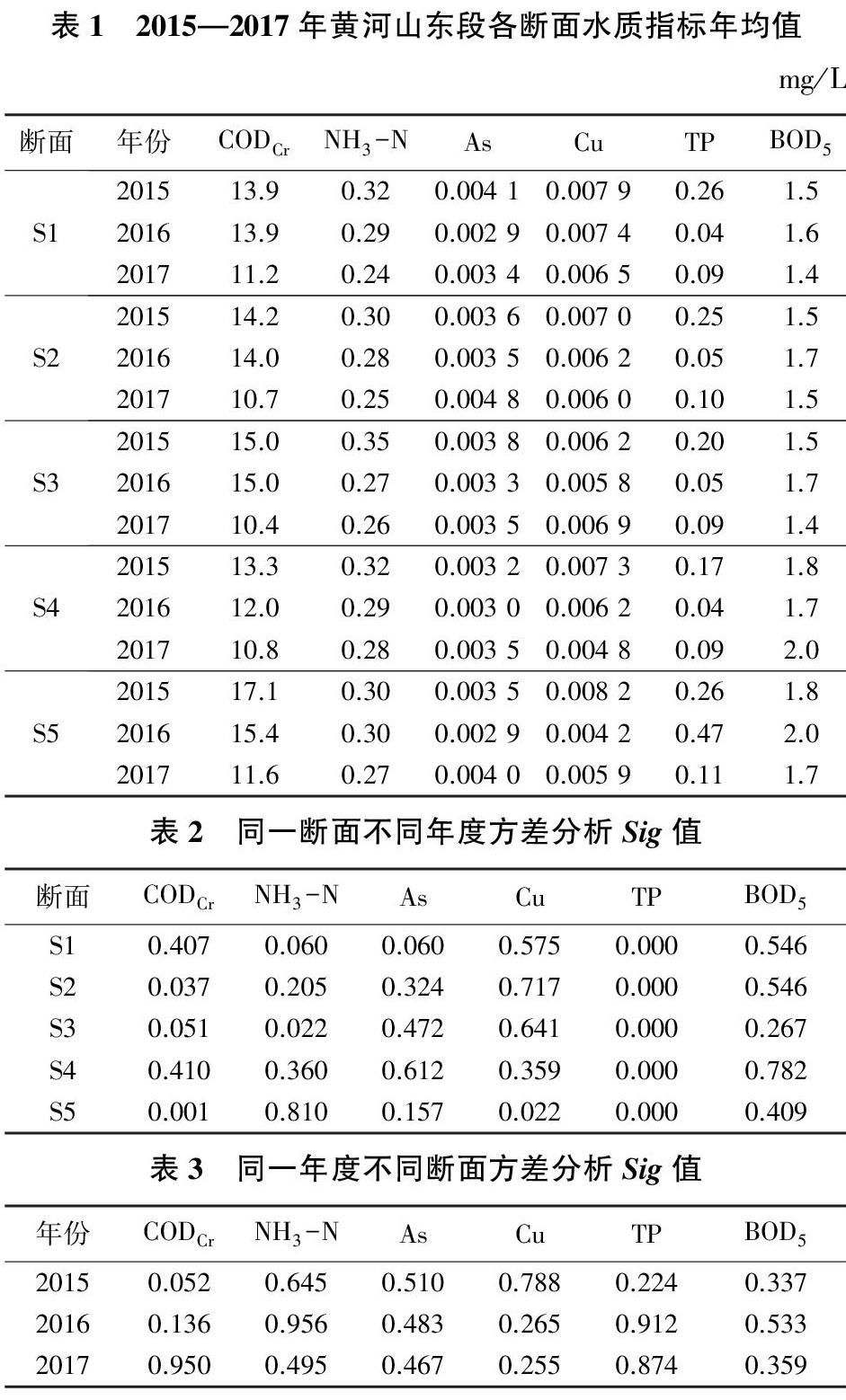
研究基礎數據來源于黃河水利委員會山東水文水資源局2015—2017年的水質監測數據，根據黃河山東段的實際水質狀況，排除一年中多數月份小于檢出限的項目，選取化學需氧量（CODCr）、氨氮（NH3-N）、砷（As）、銅（Cu）、總磷（TP）和五日生化需氧量（BOD5）作為評價指標，根據《地表水環境質量標準》（GB 3838—2002）進行水質評價。每個斷面每月進行一次水質監測，水質樣本共180個，各斷面各水質指標監測數據見表1。

2.3?數據時空尺度方差分析

考慮到水體污染物的時空差異性與相關性，對各水質評價指標進行同一斷面不同年度間和同一年度不同斷面間月度監測值的單因素方差分析，結果見表2和表3。其中：Sig值是差異性顯著的檢驗值，Sig值小于等于0.05，表明控制變量下不同水平總體平均值存在顯著性差異;Sig值大于0.05，不存在顯著性差異。結果表明，在時間上，TP存在顯著性差異，As和BOD5均不存在顯著性差異，部分斷面CODCr、NH3-N和Cu在不同年度間存在顯著性差異;在空間上，6個水質評價指標在同一年度不同斷面間均不存在顯著性差異。由此可見，各水質評價指標在時空尺度上存在差異性與相關性，根據各指標存在的相似性，將樣本進行分組評價，從而簡化評價過程，減少數據的重復計算。

2.4?樣品點分組

通過SPSS 19.0軟件用Ward法對180個水質樣本進行層次聚類分析，得到重新調整距離聚類合并的樹狀圖和聚類表，根據樹狀圖和聚類表對樣本點進行分組。根據SPSS 19.0軟件生成的聚類表，以類數為橫坐標，以離差平方和系數為縱坐標，繪制曲線（圖略），從曲線可以看出，從12類變化到11類時，曲線斜率明顯增大，因此把樣本分成12組。12組樣本對應的水質樣本點見表4。

[6]?李蓮芳，曾希柏，李國學，等.利用模糊綜合評判法評價潮白河流域水質[J].農業環境科學學報，2006，25（2）：471-476.

[7]?CHANG N B， CHEN H W， NING S K. Identification of River Water Quality Using the Fuzzy Synthetic Evaluation Approach[J]. Journal of Environmental Management， 2001， 63（3）： 293-305.

[8]?賴坤容，周維博.灰色關聯分析在延安市寶塔區延河段水質評價中的應用[J].成都理工大學學報（自然科學版），2010，37（5）：570-573.

[9]?CHENG Y Q， MA H M， SONG Q W， et al. Assessment of Water Quality Using Grey Relational Analysis and Principal Component Analysis[J]. Advanced Materials Research， 2011， 255-260： 2829-2835.

[10]?李晶.基于人工神經網絡的黃河寧夏段水質評價研究[D].銀川：寧夏大學，2013：17-28.

[11]?PALANI S， LIONG S Y， TKALICH P. An ANN Application for Water Quality Forecasting[J]. Marine Pollution Bulletin， 2008， 56（9）： 1586-1597.

[12]?LI P Y， HE S， HE X D， et al. Seasonal Hydrochemical Characterization and Groundwater Quality Delineation Based on Matter Element Extension Analysis in a Paper Wastewater Irrigation Area， Northwest China [J]. Exposure and Health， 2018， 10（4）： 241-258.

[13]?鄒葉鋒，陳鎖忠.基于物元分析的地下水質量綜合評判[J].水文，2006，26（6）：20-22.

[14]?汪明武，周天龍，葉暉，等.基于聯系云的地下水水質可拓評價模型[J].中國環境科學，2018，38（8）：3035-3041.

[15]?WONG H， HU B Q. Application of Improved Extension Evaluation Method to Water Quality Evaluation[J]. Journal of Hydrology， 2014， 509： 539-548.

[16]?付強，付紅，王立坤.基于加速遺傳算法的投影尋蹤模型在水質評價中的應用研究[J].地理科學，2003，23（2）：236-239.

[17]?ZHANG C， DONG S H. A New Water Quality Assessment Model Based on Projection Pursuit Technique [J]. Journal of Environmental Sciences， 2009， 21（增刊1）： 154-157.

[18]?馮莉莉，呂小凡，高軍省.水質評價的集對分析方法研究[J].人民黃河，2010，32（10）：76-79.

[19]?SI Q， LI M C， ZHANG G Y， et al. Set Pair Analysis Method for Water Quality Evaluation Based on Nonlinear Power Function[J]. Environment Science and Materials Engineering， 2012， 573-574： 497-500.

[20]?陳強，楊曉華.基于熵權的TOPSIS法及其在水環境質量綜合評價中的應用[J].環境工程，2007，25（4）：75-77.

[21]?LI P Y， WU J H， QIAN H. Groundwater Quality Assessment Based on Rough Sets Attribute Reduction and Topsis Method in a Semi-Arid Area， China[J]. Environmental Monitoring and Assessment， 2012， 184（8）： 4841-4854.

[22]?楊曉華，楊志峰，酈建強，等.水環境質量綜合評價的多目標決策-理想區間法[J].水科學進展，2014，15（2）：202-205.

[23]?劉國東，丁晶.水環境中不確定性方法的研究現狀與展望[J].環境科學進展，1996，4（4）：46-53.

[24]?李紹飛.區域水資源水環境綜合評價方法研究[D].天津：天津大學，2006：10.

[25]?KUO Y Y， YANG T H， HUANG C W. The Use of Grey Relational Analysis in Solving Multiple Attribute Decision Making Problems[J]. Computers & Industrial Engineering， 2008， 55（1）： 80-93.

[26]?楊蘇才，南忠仁，牛亞萍，等.因子分析在水質評價與成因分析中的應用[J].人民黃河，2006，28（5）：37-39.

[27]?LIU C W， LIN K H， KUO Y M. Application of Factor Analysis in the Assessment of Groundwater Quality in a Blackfoot Disease Area in Taiwan [J]. The Science of the Total Environment， 2003， 313： 77-89.

[28]?SHRESTHA S， KAZAMA F. Assessment of Surface Water Quality Using Multivariate Statistical Techniques： a Case Study of the Fuji River Basin， Japan[J]. Environmental Modelling & Software， 2007， 22（4）： 464-475.

[29]?ZHENG L Y， YU H B， WANG Q S. Assessment of Temporal and Spatial Variations in Surface Water Quality Using Multivariate Statistical Techniques： a Case Study of Nenjiang River Basin， China[J]. Journal of Central South University， 2015， 22（10）： 3770-3780.

[30]?周豐，郭懷成，劉永，等.基于多元統計分析和RBFNNs的水質評價方法[J].環境科學學報，2007，27（5）：846-853.

【責任編輯?呂艷梅】