淺談用傳統文化知識激發學生學習數學的興趣

張衛峰

美國心理學家布魯納曾指出：“對學生最好的刺激乃是對所學教材的興趣”。由于數學是一門具有高度抽象性、嚴謹邏輯性的學科，有的教師在教學過程不注意方法，是很多學生失去了學習數學的興趣。作為數學教師，利用中華民族歷史長河中孕育了燦爛獨特的民族傳統文化，挖掘傳統文化與數學教材知識中的結合點，讓學生利用已有的數學知識經驗，使數學與傳統文化相聯系，使其產生對數學的好奇心和求知欲，激發學生學習數學的興趣。下面就從三個方面為例來探索。

1.利用九宮圖（有名三階幻方）為例。

在人教版七年級數學第一章《有理數加法》運算這節課中，我們可以用電視劇《射雕英雄傳》中，神算子瑛姑考黃蓉“九宮圖”，黃蓉說出：“九宮之義，法以靈龜，二四為肩，六八為足，左三右七，戴九履一，五居中央”這段的視頻作為情景進行引入新課，就能吸引學生的注意力，激發了學生學習本節課的興趣。

人教版七年級數學第一章《有理數加法》運算這節課， 多次安排了在 3×3的小方格里填數的練習題. 其中， 把 1、2、3、4、5、6、7、8、9這九個自然數填進小方格，并且使圖中各行、列及斜對角的三個數字之和都相等的圖形， 叫做九宮圖，如圖所示。教室裝有多媒體設備的學校，可以給學生展示圖1這幅圖片，讓學生對數學產生好奇心，培養他們觀察分析問題的能力，就會激發學生學習數學的興趣。

隨著現代教育技術和網絡的普及，學生獲得知識方面更強更廣泛，在上完課后，可以讓學生回家后用電腦查閱幻方的相關資料，教師可以引導學生，讓學生自己提出問題，讓學生查資料解決問題，培養學生探索問題和觀察思考問題的能力。例如下面幾個問題：

1.1 三階幻方的填法和構造法出自我國古代那些書籍呢？

1.2 ?為何九宮圖各行、列及斜對角的三個數字之和為15，15是怎么算出來的？15與中心數5有和關系？

1.3九宮圖還有幾種形式？除過上圖的形式，還有幾種變式？請把變式都寫出來？

1.4九宮圖所有形式中五個奇數和和四個偶數的位置的共同點？

1.5九宮圖所有形式中各行、列及斜對角三個數的差是啥關系？

2.利用八卦圖為例。

在北師大版高中數學教材必修1中，第69頁的《正整數指數函數》一課中的“實例分析”問題1：細胞分裂時，，由1個分裂成2個，2個分裂成4個……一直分裂下去，其中一個問題為列表表示1個細胞分裂次數分別是1，2，3，4，5，6，7，8時，得到的細胞個數。教師講授本節課時可以用多媒體展示“太極生兩儀，兩儀生四象，四象生八卦”的過程來引入新課，這樣是學生更加容易理解知識，從而能很好的掌握知識，是傳統文化和教材很好的結合起來，讓學生產生學習數學的興趣。

《易經》中的“太極生兩儀，兩儀生四象，四象生八卦”，這句話中就蘊含著數學的文化知識。意思就是說太極分裂成兩儀，兩儀分裂成四象，四象分裂成八卦。用數學觀點可以理解為， 就是一個變二個，二個變四個，四個變八個，這句話中的三個“生”可以理解成數學中變化的過程，就可以把這個問題轉化成正整數指數函數模型的問題研究。在這個問題中蘊含著幾個數學知識，我們就引導學生挖掘出來，就從以下三個方面來看一下。

2.1正整數指數函數的知識：y=（n=0， 1， 2， 3）.在這就是一個自變量n為正整數0，1，2，3的正整數指數函數。

（1）n=0， ?y=1; （2） n=1， y=2， ? （3）n=2， ?y=4; ?（4）n=3， ?y=8

2.2 等比數列的知識：（圖形個數比）

1個太極圖形， 2個兩儀圖形， 4個四象圖形， 8個八卦圖形。從一個數開始，后一個數比前一個數的比值都是一個常數，那么這個數列就叫等比數列。

2.3等比數列求和的知識：（圖形個數和）

1個太極圖形+ 2個兩儀圖形+4個四象圖形+8個八卦圖形=15個不同的圖形。

3.利用公元紀年法和成干支紀年法為例。

在初中歷史課本中會遇到一些重要的歷史事件，例如甲午戰爭、戊戌變法、辛亥革命等。學生不知道怎么命名，這些問題是涉及到兩種紀年法——公元紀年法和干支紀年法的問題。為此，以數學觀點來闡述這個問題。

3.1讓學生知道干支紀年的有關初步知識。

3.1.1首先關鍵就在先弄懂什么是天干與地支。

天干有10個，即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;

地支有12個，即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥

3.1.2弄懂什么是天干與地支排列組合規律。干支是天干和地支的合稱。

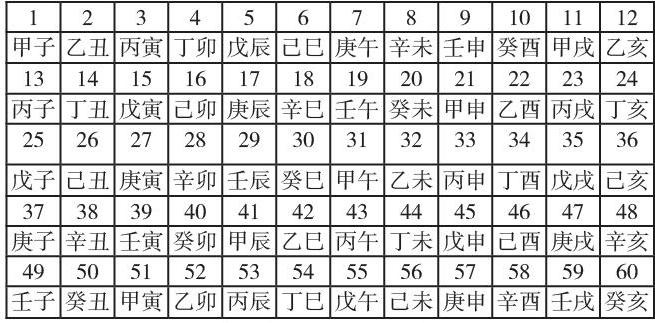
天干和地支從“甲子”開始，按順序逐一相配，各用到最后一個時，再從第一個開始繼續相配，從而形成了 60 個干支，也稱“六十花甲子”。周而復始，循環記錄，這就是俗稱的“干支紀年”。這里蘊含了數學中的排列組合知識。

3.2六十花甲和干支紀年里蘊含的數學知識。

天干10個，地支12個，10和12的最小公陪數就是60，這就是六十花甲中的六十的來源，學生就很明白原來用數學中的最小公陪數的知識理解。

天干與地支排列組合，是高中數學知識的組合知識，不是排列知識。干支紀年中也蘊含了周期現象的數學知識。

三階幻方、八卦圖和公元紀年法換算成干支紀年法是很難得的好教材. 它對于培養學生學習數學的興趣，熱愛數學， 熱愛生活， 勤于思考， 勇于探索，并學會如何觀察問題， 如何發現問題， 如何轉化分析， 如何證明結論， 如何總結提煉都有重要作用， 老師們應當盡力挖掘教科書的潛在教育功能， 既注意眼前的近期目標， 又注意未來的長遠目標。