基于貝葉斯網絡分類算法的采摘機器人故障診斷研究

李卓然

(羅定職業技術學院 電子信息系,廣東 羅定 527200)

0 引言

隨著科學技術的發展,采摘機器人在水果、蔬菜等采摘方面取得了廣泛的應用。由于采摘機器人工作環境復雜、零部件眾多,故障率也較高,而一旦其發生故障,會對用戶、工作空間和采摘對象造成傷害。因此,實現對采摘機器人的故障診斷,一直是一個非常重要的研究領域。本文研究的基于貝葉斯網絡分類算法的采摘機器人故障診斷,將貝葉斯網絡和故障特征分析結合起來,能夠實現采摘機器人動力故障和執行器的故障診斷。

1 貝葉斯網絡分類算法

貝葉斯網絡是基于概率理論的統計模型,是一種非常重要的定量模型求解方法,具有豐富邏輯理論和數學模型。

1.1 貝葉斯定理

1)條件概率理論:假設存在A、B兩個獨立的事件,其中A事件發生的概率大于0,則

(1)

其中,P(B|A)為A事件發生的基礎上B也同時發生的概率。

2)聯合概率理論:假設存在A、B兩個獨立的事件,其中A事件發生的概率大于0,則兩個事件的聯合概率為

P(A·B)=P(A)P(A|B)

(2)

其中,P(A·B)為兩個事件同時發生時的概率。

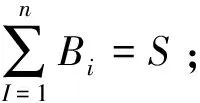
(3)

4)貝葉斯分類理論:根據前面介紹的3種概率公式,可以推導出貝葉斯分類計算公式,即

(4)

以上公式是貝葉斯分類的基礎。

1.2 貝葉斯網絡分類

1)貝葉斯網絡分類概述。采摘機器人故障診斷的基礎是建立從故障征兆到故障特征的映射關系,其理論基礎是根據故障征兆變量確定故障類型。貝葉斯網絡分類算法是一種典型的統計學分析方法,根據貝葉斯理論,研究故障發生的先驗概率與后驗概率結合起來,根據先驗概率和樣本集求出后驗概率值。

假設U={X1,X2,…,Xn,C}為離散變量的集合,Xi為屬性變量,C為類變量集合,xi是Xi的取值。實例Ii=(x1,x2,…,xn)為類cj的概率,可以用貝葉斯公式表示為

(5)

其中,P(cj)為cj的先驗概率,P(ci|x1,x2,…,xn)為cj的后驗概率。式(5)可以改寫為

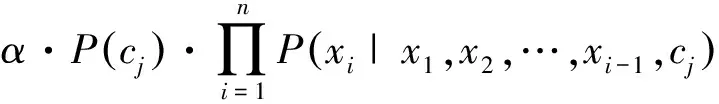
(6)

其中,α為正則參數。從式(6)可以看出:貝葉斯算法選擇P(ci|x1,x2,…,xn)最大的類cj為Ii的類標簽,因此貝葉斯算法的核心是求解P(ci|x1,x2,…,xn)的值。

本文將介紹樸素(NaiveBayes,NB)和TAN(Tree Augmenetd Naive Bayesian,ATN)兩種貝葉斯分類方法。

2)NB貝葉斯網絡分類器。NB貝葉斯網絡分類器的原理是設定其變量條件之間相互獨立,每個屬性只和類變量C關聯,這一條件極大程度地降低了貝葉斯算法的復雜度,其計算公式可以表示為

(7)

雖然存在著一個變量相互獨立的假設,但是NB貝葉斯網絡分類器仍具有相當高的健壯性和有效性,分類精度也非常高。NB貝葉斯網絡分類器模型如圖1所示。

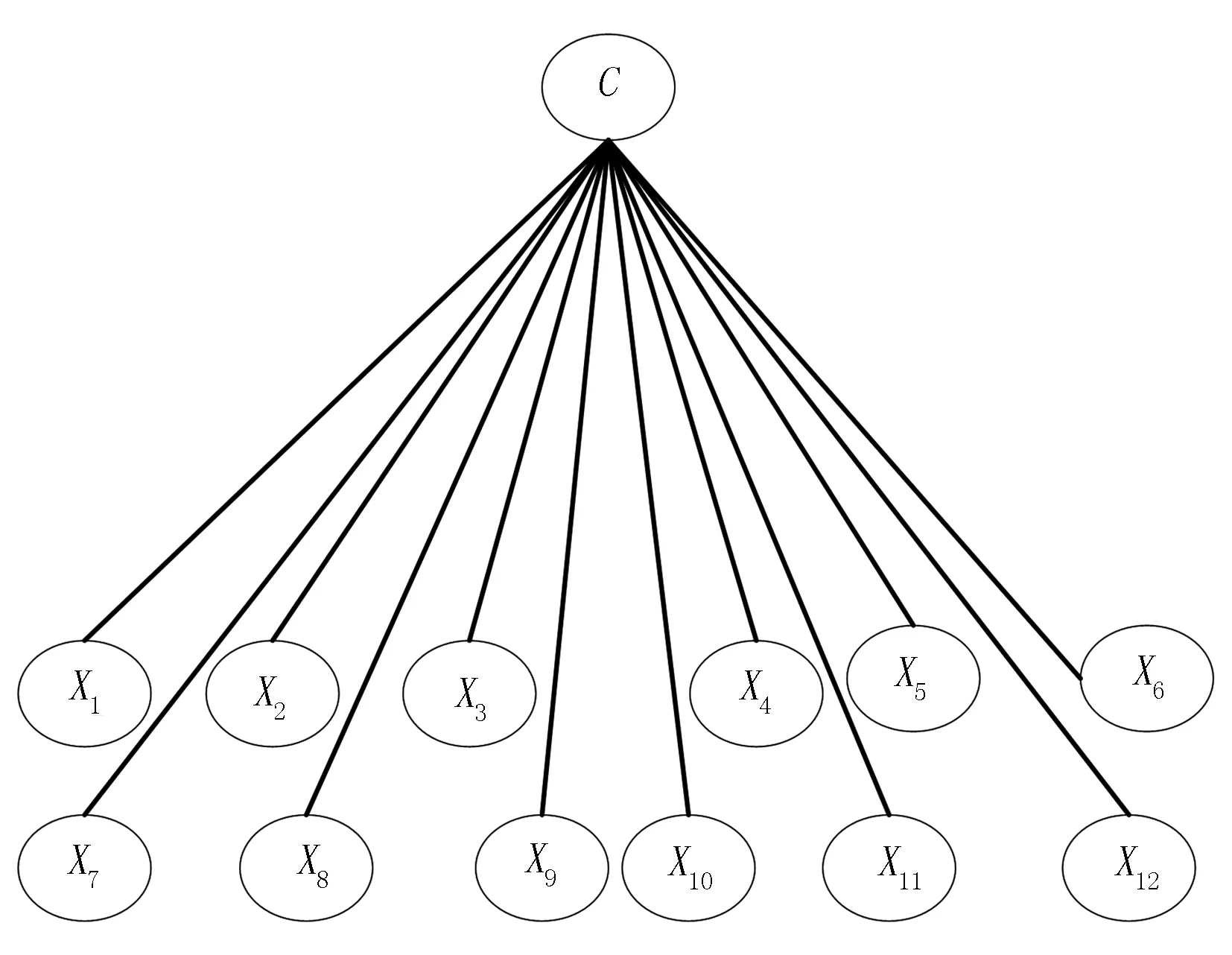
圖1 NB貝葉斯網絡分類器模型

3)TAN貝葉斯網絡分類器。TAN貝葉斯網絡分類器是針對NB模型的進一步優化改進,其假設變量之間符合樹狀結構,而不要求變量條件之間相互獨立,允許多個節點變量同時依賴一個節點變量,滿足學習速度和精度之間的一種平衡,其計算公式可以表示為

(8)

其中,Pαi為xi的父節點,分為類節點與屬性變量等兩類。

TAN貝葉斯網絡分類器也同樣具有高效性和較高的分類精度,模型如圖2所示。

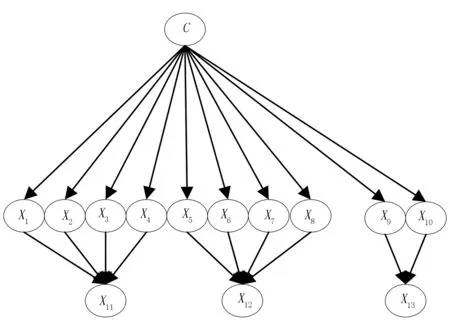
圖2 TAN貝葉斯網絡分類器模型

2 采摘機器人故障診斷貝葉斯網絡模型

2.1 采摘機器人故障診斷節點的選取

采摘機器人是一個零部件多、機械結構復雜的系統,由行走機構、電機驅動、末端執行器、傳感器結構、控制器和機器人本體構成。行走機構為采摘機器人提供行進動力;電機驅動用來控制采摘機器人的前進、后退、轉彎及采摘手臂的姿態控制等;末端執行器用于采摘目標水果,傳感器結構用于獲取采摘機器人采摘手臂的姿態信息。采摘機器人結構如圖3所示。

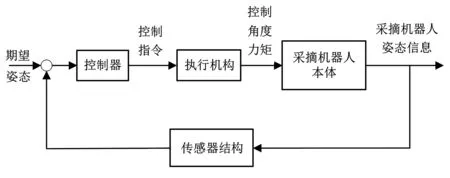
圖3 采摘機器人結構示意圖

采摘機器人行走機構包括轉向輪、推力器,以及傳感器結構位置、力度和角度等姿態傳感器;末端執行器是采摘機器人之重要部件,采摘機器人能夠完成采摘任務主要依靠末端執行器,因此末端執行器的故障會影響整個系統的性能。

綜上,本文選取轉向輪、推力器、位置傳感器、力度傳感器、角度傳感器和末端執行器為故障診斷參數。

在實際的故障分析中,采集到的數據都是連續的,先需要進行數據離散處理,然后利用貝葉斯網絡分類器進行分析。本文研究的故障診斷參數離散化如表1所示。

從表1可以看出:故障診斷參數分為正常、故障和嚴重故障3個等級, “正常”表示采摘機器人運行正常,“故障”表示采摘機器人運行壽命縮短,“嚴重故障”表示采摘機器人功能將異常或完全失效。

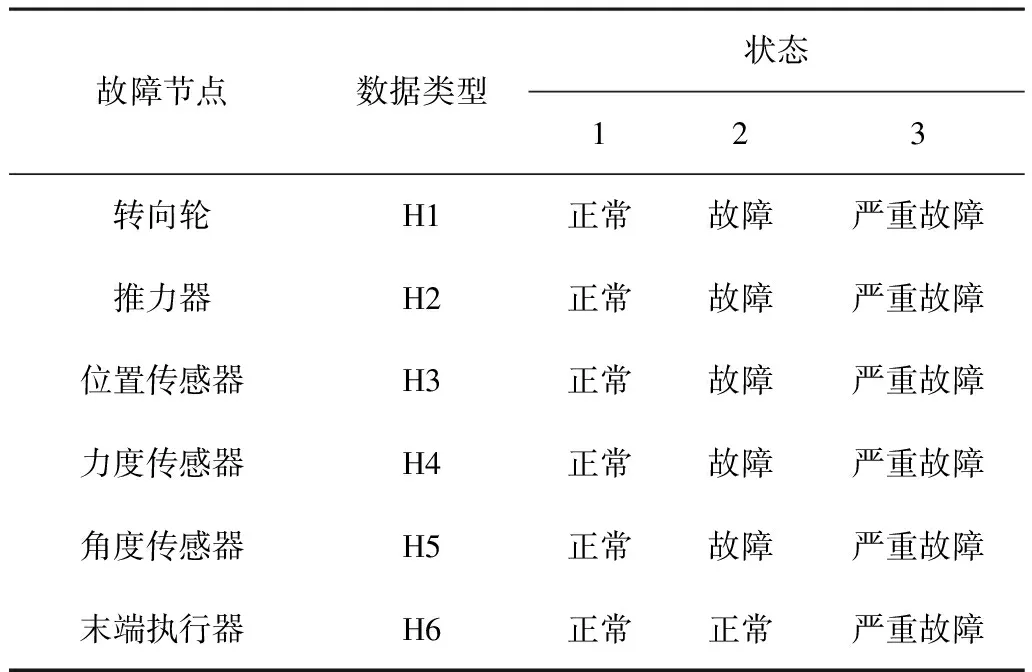
表1 采摘機器人故障診斷參數離散化

2.2 建立采摘機器人故障診斷貝葉斯網絡模型

為了實現對采摘機器人故障進行分析和診斷,本節在上一節的基礎上,建立采摘機器人故障診斷貝葉斯網絡模型。根據采摘機器人運動控制、末端執行器執行原理,可以分層建立采摘機器人故障診斷貝葉斯網絡的拓撲圖。第一步,建立貝葉斯網絡的根節點,即為轉向輪、推力器、位置傳感器、力度傳感器、角度傳感器和末端執行器等6個節點;第二步,通過邏輯分析,確定以上6個節點和行走機構、傳感器結構、末端執行器之間的連接方向。本文建立的采摘機器人故障診斷貝葉斯網絡模型如圖4所示。

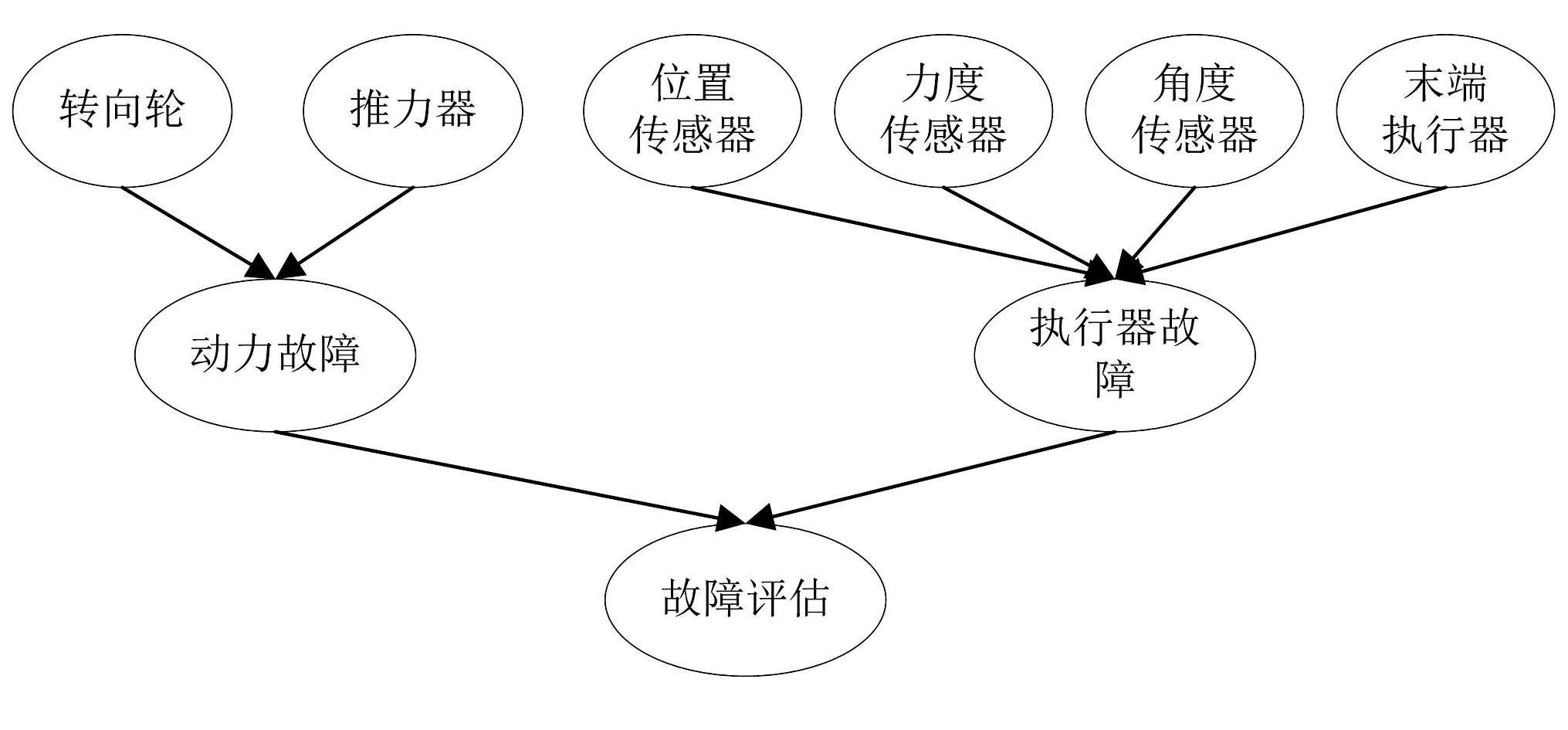
圖4 采摘機器人故障診斷貝葉斯網絡模型

2.3 確定貝葉斯網絡節點參數

確定貝葉斯網絡節點參數的實質是確定節點的條件概率分布,但在這之前需要提前確定節點的驗前分布。在實際研究中,一般會假設系統參數的驗前分布狀態是已知條件。本文取Beta(p,a,b)分布作為采摘機器人故障診斷貝葉斯網絡中節點的驗前分布,具體的驗前分布信息如下:

1)節點p的均值P0條件已知,則

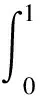
(9)

2)驗前分布節點參數a、b或者p的最小值已知,則

a≥a-,b≥b-或p≥p-

(10)

3)點參數p的置信區間[p1,p2]已知,則

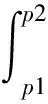
(11)

假設P0條件已知,可以根據驗前概率密度獲取a和b,即

(12)

確定節點的條件概率分布主要是計算參數a、b的最優值及π(p)的熵,則

H(Beta(p,a,b))=HB(a,b)=

(13)

假設P0已知,則聯立式(9)和式(13)可得

a/(a+b)=p0

(14)

因此,可以將a*、b*最優求解問題轉換成多個約束條件下求極值的問題,則

(15)

利用式(15)可以求出節點參數驗前分布的概率分布參數,通過SOC神經網絡算法進行訓練后,即能夠為采摘機器人故障診斷提供依據。

3 實驗與分析

采用TAN貝葉斯網絡分類器模型和SOC神經網絡結合的方式對采摘機器人特征參數進行故障診斷分析。

3.1 SOC神經網絡方法

SOC神經網絡是一種無監督的網絡算法,其可以對輸入的數據參數進行聚類分析。SOM神經網絡整體架構如圖5所示。

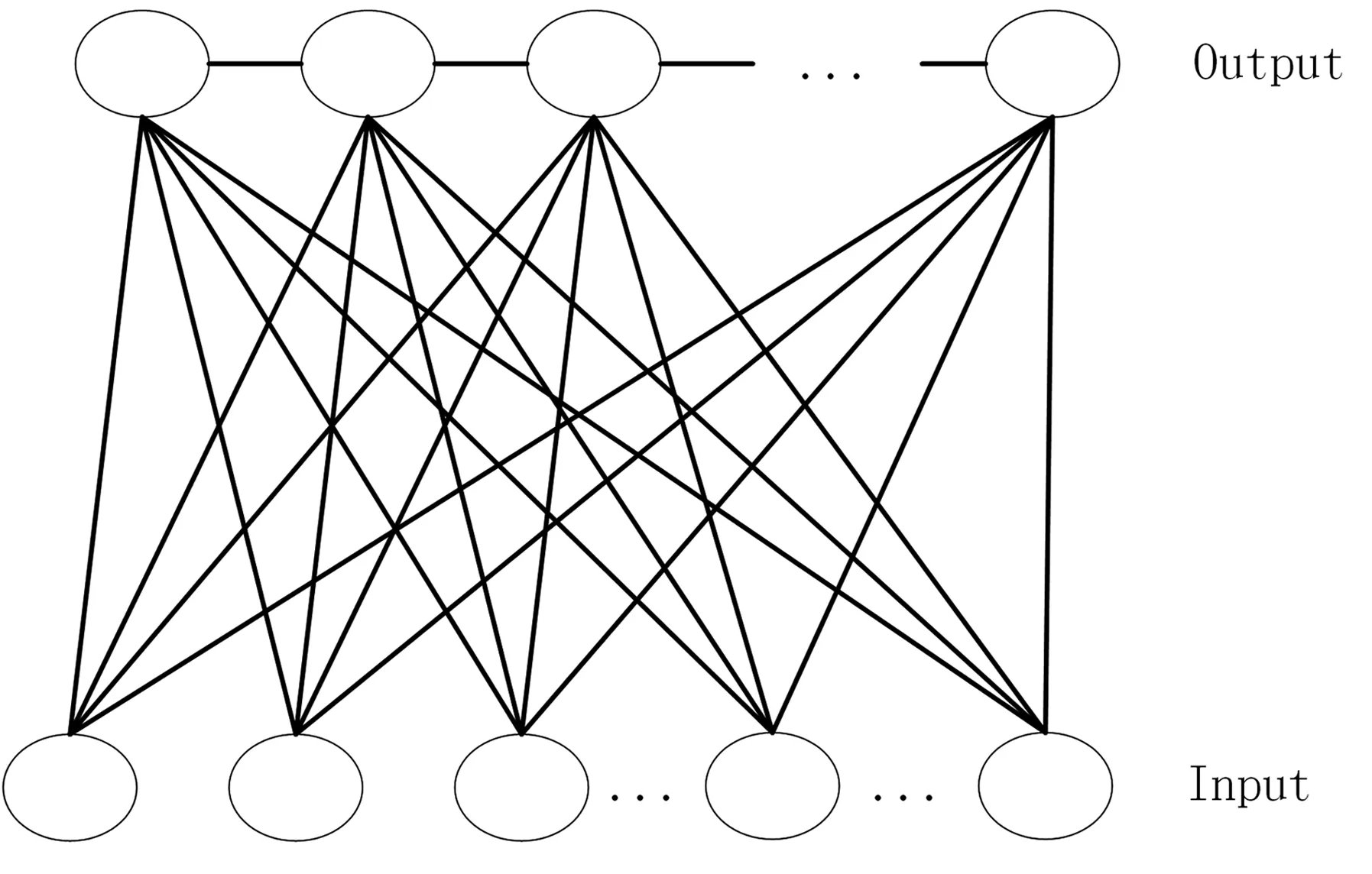
圖5 SOM神經網絡整體架構

SOM神經網絡實現的流程主要有:

1)設置初始權值。SOM神經網絡的初始權值為Wi,j(t)為a,介于0～1之間,同時設置算法的初始領域N(0),學習率為η(t),迭代次數為T。

2)選出輸入神經元。在采集到參數節點的數據中選出一組Xk作為輸入的初始神經元,即

(16)

3)計算歐式距離。利用SOC神經網絡算法,計算出Xk與各個神經層之間的歐式距離dj,k,即

(17)

其中,j為神經元個數。

4)求出最優的神經元,即

dj,k=min(d1,k,d2,k,…,dp,k)

(18)

5)修正權值W為

Wi,j(t+1)=Wi,j(t)+η(t)hb,j(t)[Xi(t)-Wi,j(t)]

(19)

(20)

其中,b為最優領域節點,rb、rj為輸出節點在點b、j的位置。

一直重復步驟1)～步驟5),直到t從0到T。

3.2 診斷結果分析

為驗證本文設計的基于貝葉斯網絡分類算法的采摘機器人故障診斷系統設計的可行性和可靠性,利用上訴診斷流程,對NB和TAN2種貝葉斯分類方法進行了對比分析,故障診斷結果如表2所示。

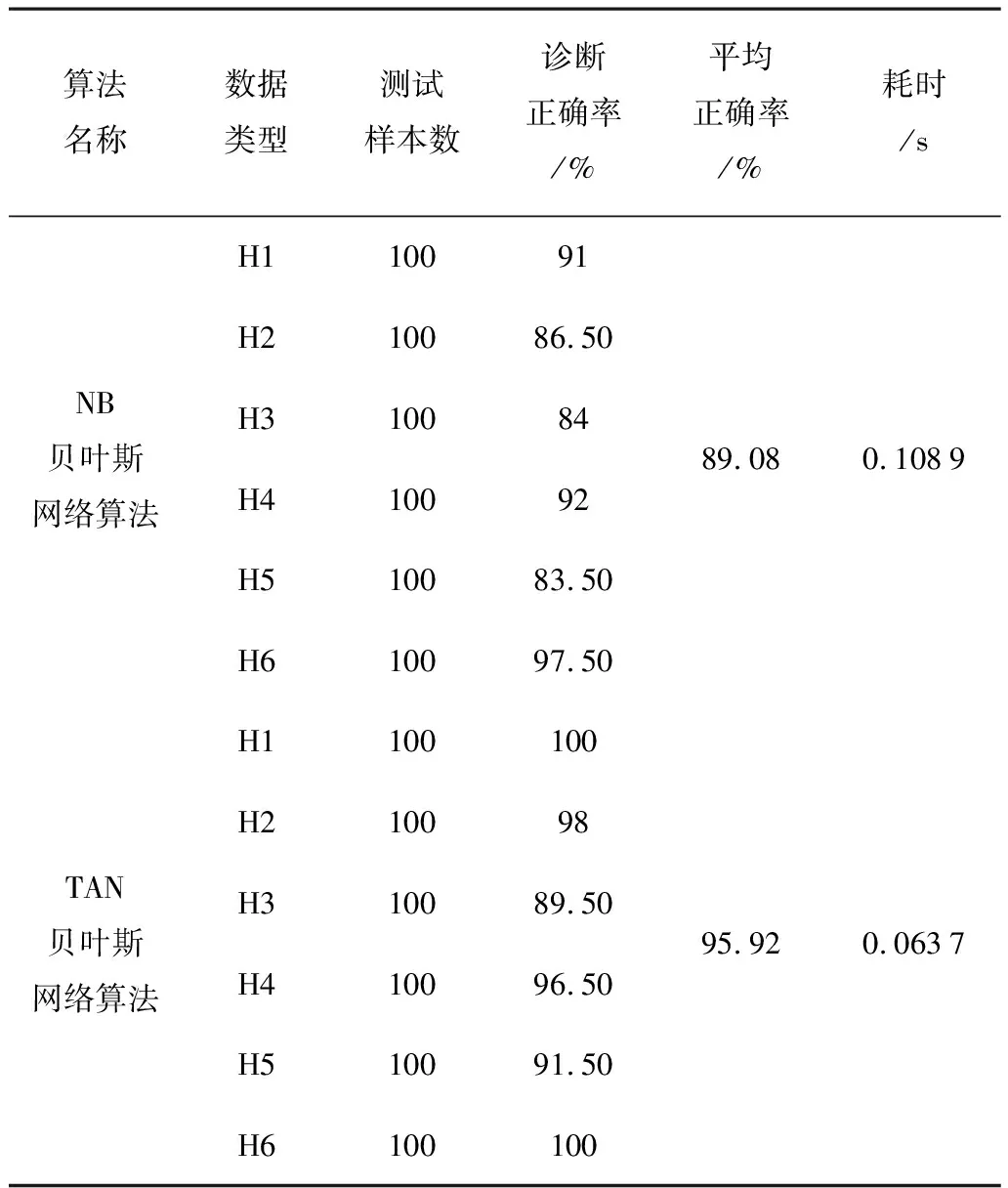
表2 采摘機器人故障診斷結果對比

由表2可以看出:無論從故障診斷平均正確率還是耗時時間,TAN貝葉斯網絡算法相比于NB算法都有很大的提高;在故障診斷正確率方面,TAN貝葉斯網絡算法高達95.92%,比NB貝葉斯網絡算法高了近7個百分點;在耗時時間方面,TAN貝葉斯網絡算法僅需要0.063 7s,比NB貝葉斯網絡算法縮短近40ms。因此,基于貝葉斯網絡分類算法的采摘機器人故障診斷系統,不僅適用于采摘機器人動力故障,對執行器故障也具有相同效果,且能較大地提高故障診斷正確率和效率。

4 結論

針對貝葉斯網絡算法進行了介紹和研究,并在此基礎上建立了采摘機器人故障診斷貝葉斯網絡模型,能夠實現采摘機器人的動力故障和執行器故障的診斷檢測。實驗結果表明:在故障診斷正確率方面,TAN貝葉斯網絡算法比NB算法高了近7個百分點;在耗時時間方面,TAN貝葉斯網絡算法NB算法縮短近40ms,說明該系統不僅適用于采摘機器人動力故障和執行器故障診斷,且能夠較大的提高故障診斷正確率和效率。