城市道路同向窄路段車速統計特性研究*

韓寶睿 宋婉璐 于曉妹 周 玉

(南京林業大學汽車與交通工程學院1) 南京 210037) (江蘇交科能源科技發展有限公司2) 南京 210000)

0 引 言

同向窄機動車道是指部分路段存在車道寬度小于最小規范值(3.0 m)的具有同向雙車道的城市道路，該類道路由于車道較窄，駕駛人在跟馳與超車或并行時的操作行為與較寬車道有一定差異，反映在交通流上也存在一定差異.關于窄車道的研究，以往主要從交叉口窄車道的通行能力效率及駕駛行為分析，山區窄車道的交通流特性分析等方面進行.Sapna[1]指出車道寬度是影響駕駛車速的限制因素，隨著車道寬度的增加，地點車速方差及相鄰車輛的速度差異都有所增加，合理設置道路車道寬度有利于限制車速波動.陳云等[2]以杭州市道路整治工程為例，通過駕駛人對窄車道的適應性問卷調查，定性驗證了窄車道可以有效減少駕駛人的變道行為.韓寶睿等[3]通過建立仿真模型，得到了禁止超車的窄雙車道的會車率與流量關系.目前，國內外對于車速與通行能力關聯性研究主要以《道路通行能力手冊》(2010)(以下簡稱HCM)為參考標準.但是，HCM中并未提及車道寬度在小于3 m時的通行能力折算系數.目前，國內北京、武漢、南京等城市部分道路，已經采用車道寬度小于3.0 m的機動車道[4].總體來說，車道寬度已呈現變窄趨勢.

本文旨在通過對窄車道車輛車速的離散性進行分析，并將窄車道寬度與其自由流車速進行關聯性研究，提出在窄車道條件下車速分布特征及車道寬度為2.8 m時的自由流速度折減系數，為窄車道道路斷面建設提供理論基礎的支持.

1 窄機動車道車速統計特性研究

1.1 觀測路段情況概述

選取南京市富貴山分離式雙向四車道道路為研究對象，分離式道路橫斷面可有效消除對向車輛的側向影響.該道路全長1 425 m，其中隧道段長500 m，全線限速50 km/h.路段無監控設施，可以認為車速僅受到限速標志與道路條件影響.交通組成基本以小型客車為主(占總交通量的92%)，實施大貨車全天限行措施，大型客車占總交通量的6%.該道路為封閉式道路，全段無出入口連接，外部環境干擾較小.經道路實勘，得到了其橫斷面見圖1，其中機動車道寬度、路緣帶寬度、側分帶寬度分別為2.8，0.3及1.3 m.

圖1 富貴山分離式半幅橫斷面

1.2 地點車速調查結果統計分析

利用攝像法對富貴山窄車道早、晚高峰的地點車速數據進行采集，獲得了578個有效樣本，并通過SPSS的P-P,Q-Q正態性檢驗，證實其基本符合正態分布(即變量近似成為一條直線)，見表1和圖2.

表1 車速頻率分布表

圖2 車速分布正態檢驗

1.3 窄道與標準車道車速離散性對比分析

為了比較車道寬度為2.8 m的窄四車道特有的車速離散性特征，另外選取了南京市花園路、御道街及板倉街(雙向四車道段)三條城市雙向四車道，其車道分別寬度為(3.0，3.5及3.75 m)，對其地點車速進行觀測統計，見表2.為了排除時間因素對實驗結果的影響，調查時間與富貴山窄道地點車速調查時間一致.

表2 不同車道寬度地點車速特征值

引入離散系數概念，即用標準偏差與平均值的比值作為離散性分析的統計量，消除平均數不同對離散程度的比較影響[5].

經調查，富貴山窄道的高峰小時交通量與其他道路交通量的最大相對差值僅為14%，平均每5 min的相對差值僅為1.17%，在一定程度上，交通量的差異沒有對車速起到較大干擾.表中窄車道的車速極差均高于其他道路水平，但是其離散系數卻呈現較低水平.這說明，雖然窄車道不能對所有駕駛人的行車車速起到約束作用，但是對于大部分駕駛人(特別是處于跟車狀態的車輛車速)能夠起到較為明顯的約束效果，直觀數據表現為車輛車速離散程度較低，車速分布較為集中.對于窄車道，由于道路寬度限制，實施換道行為的難度增加，大部分車輛仍會選擇跟馳行駛，形成有秩序的排隊車流狀態，從而車速分布更加均勻.

2 窄車道自由流車速折減系數的擬合與驗證

HCM關于自由流車速的車道寬度修正值僅涉及到車道寬度在3.0～3.6 m的情況.由于土地資源、地形地勢等原因限制，我國仍存在部分寬度小于3.0 m的道路，為了使得該手冊能夠更好地適用于我國道路，本文進行了車道寬度為2.8 m時的修正值分析.

2.1 基于統計學原理的實際自由流速度確定

1) 自由流車速數據的采集 為了盡可能保證錄像法采集的車速樣本處于自由流狀態，僅選取調查斷面上10 s檢測周期僅有1輛車通過且車輛的空間占有率<12%(道路長度約為40 m)的數據作為分析對象[6-7].以2.5 km/h為組距，得到了121組自由流車速值.利用Grubbs[8]檢驗有效數據經計算，得到有效數據118組，無效數據3組.其頻率統計圖見圖3.

圖3 自由流車速頻率分布統計圖

利用SPSS計算自由流車速頻數分布直方圖對應的正態分布曲線特征值，得到了窄四車道自由流車速的正態分布特征值：μ(期望)=48.28 km/h，σ(標準差)=7.004 km/h.

2) 正態分布檢驗 正態分布檢驗采用Kolmogorov-Smirnov法進行檢驗，如果相伴概率小于等于顯著性水平α，則拒絕原假設H0，認為樣本來自的總體與指定的水平分布有顯著性差異；如果相伴概率值大于顯著性水平α，則不能拒絕原假設H0，認為樣本與指定的分布無顯著性差異[9].

依據上述水平，對自由流車速進行K-S正態性檢驗，并設定顯著性水平為0.05.得到其Sig(相伴概率值)=0.649>0.05，表示樣本數據接受原假設，符合正態性檢驗，見表3.

表3 Levene方差齊次性檢驗表

3) 穩定性分析 為了研究在不同日期的自由流車速是否會有差異，本次研究采集四個不同日期、星期的樣本車速進行上述過程的正態分布曲線繪制，并計算出其μ與σ，采用Levene方差齊次性檢驗對不同日期的期望自由流速度進行方差分析.其中顯著性水平設置為0.05.

計算得顯著性水平0.936>0.05,表明不同日期下的車速方差并無顯著性差異，這說明在不同日期下得到的自由流車速是穩定的[10]，見表4.

表4 自由流車速穩定性分析表

2.2 窄車道理論自由流折減系數的分析

1) 理論車道寬度的自由流修正系數 通過對已有的HCM中不同車道寬度對應的自由流速度減少值進行不同函數的擬合分析，得到其誤差平方和與其確定系數關系見表5.

表5 多種函數擬合參數值對比

經過比較高斯(Gsussian)函數的誤差平方和(SSE)接近于0，確定系數(R2)=0.996 6接近1，表明擬合度最好，故車道寬度與其折減系數呈現高斯函數遞減關系，見圖4.

圖4 車道寬度-自由流車速折減的Gaussian函數曲線

表達式為

y=12.82×e-(x-2.819)/0.415 5)2

(1)

當車道寬度為2.8 m時，其對應的自由流速度減少值應為12.79 km/h.

2) 計算理論自由流速度 HCM中指出，基礎自由流速度(BFFS)為

FFS=BFFS-fLW-fLC-fM-fA

(2)

式中：BFFS為基礎自由流速度，km/h；FFS為自由流速度估計值；fLW為車道寬度修正系數；fLC為側向凈寬修正系數；fM為中央帶類型修正系數；fA為入口點修正系數.

①基礎自由流速度 速度限制是自由流速度的一個重要影響因素[11].HCM中指出，在理想條件下的多車道道路的自由流速度，當速度限制為50～55 km/h，大約高出限速14 km/h;65～70 km/h時，大約高于限速11 km/h；80～90 km/h，大約高于限速8 km/h.

經調查顯示，富貴山窄四車道限制速度為50 km/h，故其基礎自由流速度約為64 km/h.

②車道寬度修正系數 據上述高斯函數自由流速度折減系數擬合公式，窄四車道在車道寬度為2.8 m時，其自由流折減系數為12.79 km/h.

③側向凈空修正系數 HCM中列出了因路旁或中央帶固定障礙物的側向凈寬造成的自由流速度下降.其中，側向凈寬包括左側向凈空與右側向凈空的自由流速度折減.通過富貴山道路條件調查可知，左側平均側向凈空為0.8 m，右側平均側向凈空平均為1 m.HCM指出，當總側向凈空為1.8 m時，其自由流速度減少值為2.1 km/h.

④中央分隔帶類型及出入口密度修正系數 本次實驗區域選于分離式道路，已進行空間交通分隔，故不用考慮中央帶類型.經查HCM得當道路設有中央分隔帶，其自由流速度折減系數為0 km/h.

HCM中提出，在有分隔帶的道路，道路出入口密度由行進方向右側出入口(也就是交叉口和進出支路)的總數除以路段總長度(以km計)來決定.富貴山道路為封閉道路，故出口密度修正值為0 km/h.

上述修正系數確定后，通過式(2)可計算得在車道寬度為2.8 m時的理論自由流速度折減系數為49.11 km/h.

2.3 車道寬度修正系數顯著性檢驗

顯著性檢驗是事先對變量的參數或分布形式做出假設然后利用樣本信息來判斷這個假設(備擇假設)是否合理，即判斷總體的真實情況與原假設是否有顯著性差異[12].本次顯著性檢驗采用單總體t檢驗方式，其統計量為

(3)

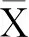
建立原假設H0：λ(理論自由流車速)=49.11，及備擇假設H1：λ≠49.11.選擇雙側檢驗，并設置顯著性水平為0.01，計算得t=0.251 6.判斷：當顯著性水平取0.01時臨界值t(3)0.01=5.841>0.251 6，故接受原假設H0.表示理論值49.11可代替窄四車道平均自由流車速水平，即車道寬度在2.8 m時的自由流折減系數12.79是通過驗證的.

3 結 束 語

運用SPSS、Matlab等軟件，通過對窄車道與標準車道的車速數據進行離散性分析，證實在交通量基本呈同一水平時，窄車道的車速離散系數最低，車速分布最為集中，說明窄車道對車速有明顯的約束作用.

通過對窄道自由流車速總樣本進行統計，對樣本數據進行了K-S正態檢驗及穩定性分析，獲得了具備代表性的自由流車速值.并基于HCM原有的車道寬度(3.0～3.6 m)與其自由流折減系數規律，建立了車道寬度—自由流速度折減的高斯函數曲線.從而得到了當車道寬度為2.8 m，有中央分隔帶(或者分離式道路不考慮中央分隔帶)，總側向凈空為1.8 m，路段中無出入口影響的路段條件，其自由流折減系數為12.79 km/h.并通過了與實測自由流車速特征值的顯著性分析，進一步驗證了結果的準確性.本文已經提出了一套方法，如需其他窄車道寬度或者道路橫斷面條件的自由流折減系數，可結合已得到的高斯函數模型及HCM中不同道路條件的修正系數計算即可.

以上結論均證實了，在窄道條件下，能夠約束駕駛人行車車速，從而使車速分布更加均勻，使道路交通更加安全、有序.本文不足之處是，在車速離散性研究方面，用于對比的道路案例較少，在自由流車速折減系數方面，缺少不同側向凈空的研究分析，后續工作將對此進行深入研究.