基于自抗擾的無刷直流電機控制系統研究
歐陽名三 閆中文
(安徽理工大學,安徽 淮南 232001)
無刷直流電機在電動車、機器人、航空航天等領域內都有著廣泛的應用[1]。隨著應用領域的不斷發展延伸,各種控制策略和算法也不斷的出現,傳統PID算法在無刷直流電機的強耦合性方面的控制效果不夠理想[2]。控制過程中存在響應速度慢、調節時間長、超調量大等問題[3]。因此,一些新的控制算法被人提出來。文獻[4][5][6]中采用模糊PID控制器,但模糊PID控制器參數計算量較大,往往控制過程不是很容易實現。自抗擾自適應控制算法是在改進PID算法缺陷基礎上結合現代控制理論提出的一種新型控制算法[7,8],其特點是具有天然的解耦性,以及幾乎和模型無關等,非常適用于無刷直流這類具有強耦合性的控制系統。
一、BLDCM的數學模型
無刷直流電機控制系統為兩兩導通方式,其電壓平衡方程為[9]:

式中,Ua,Ub,Uc為相電壓,ia,ib,ic為相電流,R 為電阻,L、M 分別為自感及互感 ea,eb,ec反電動勢。
電磁轉矩方程為:
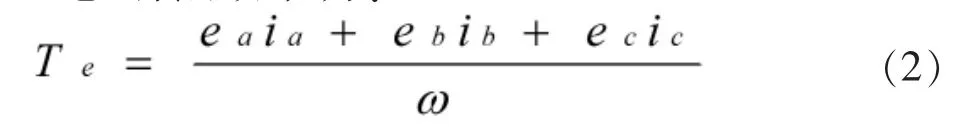
式中,Te為電磁轉矩(Nm),ω為機角速度(rad/s)。
運動方程可表示為:
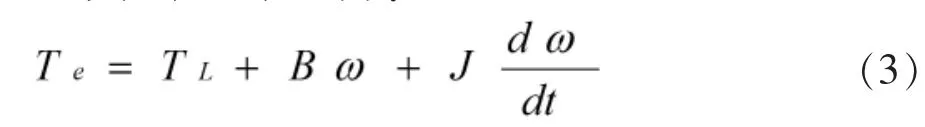
式中,TL為負載轉矩(Nm),B為阻尼系數(Nm·s/rad),J為轉動慣量(kg·m2)。
由(1)式當中的電壓方程變形可得BLDCM的狀態方程。
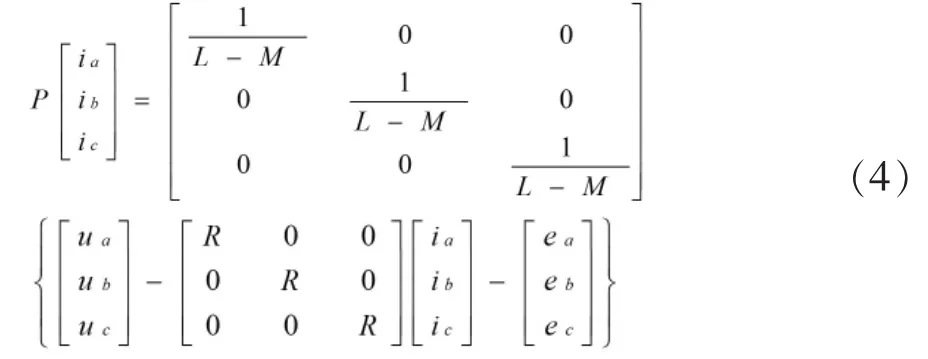
二、自抗擾控制器(ADRC)的設計
自抗擾控制是在改進經典PID固有缺陷的基礎上,而逐步形成的新的控制策略(或控制算法),其優點是對控制系統對象的模型不依賴[10],對擾動適應性較強,而且魯棒性以及可操作性也非常好。
(一)自抗擾控制器組成
自抗擾控制器分為跟蹤微分器(Tracking Differentiator)、非線性狀態誤差反饋控制器(Nonlinear State Error Feedback law)以及擴張狀態觀測器(Ex-tended State Observer)三個部分,其基本結構圖如圖1 所示[11]。
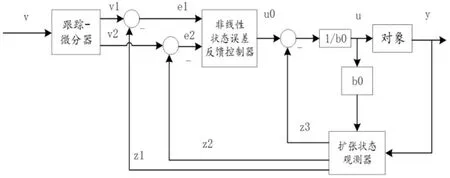
圖1ADRC結構圖
跟蹤微分器(TD):對系統的初值進行安排過渡過程,能夠得到v的近似值v1和v的微分v2。無論v是何種狀態,通過跟蹤微分器(TD)都能使v1和v2連續,能夠解決超調和響應速度問題。
擴張狀態觀測器(ESO):根據擾動狀態觀測的思想,把對輸出有影響的擾動變量擴張成一個新的狀態觀測變量,建立一個能夠準確地觀測擴張后狀態變量的觀測器,即為擴張狀態的觀測器。擴張狀態觀測器并不需要依賴于擾動的模型,也不需要直接測量擾動就可以得到擾動的估計值。
非線性狀態誤差反饋控制器(NLSEF):通過跟蹤—微分器系統能夠產生過渡過程的誤差信號和誤差微分信號,并且能夠生成誤差積分信號,將三種控制信號按一定的控制規律互相組合起來,形成了組合的控制器。三種信號既可以互組合成和PID控制相似的線性組合控制器,也能組合成獨特的非線性控制器。
(二)ADRC數學模型
1.TD的數學模型
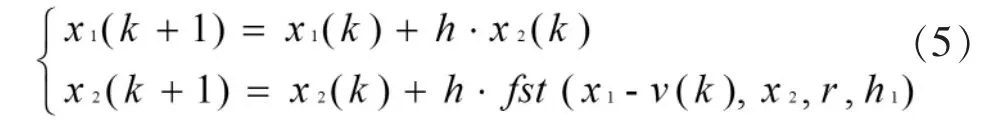
其中x1用于跟蹤信號v(t),x2用于跟蹤v(t)的導數,其中 x1、x2和 v1、v2一樣,一個用于跟蹤信號,一個是微分信號。fst是如下的非線性函數。
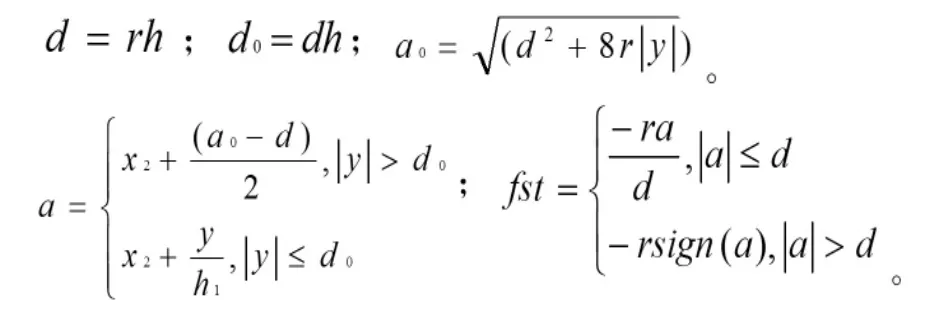
式中,h是數值積分的步長,r是跟蹤速度的參數,h1是噪音濾波效應的參數。
2.ESO的數學模型
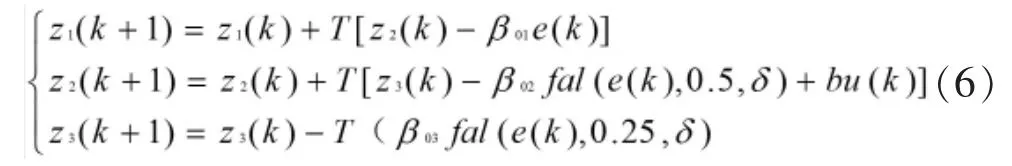
z1(t),z2(t)為狀態變量的估計。z3(t)而對不確定模型和外擾的進行估計。β01,β02,β03和 b 是可調參數。δ為濾波因子。δ的取值范圍一般為:5T≤δ≤10T。
fal為非線性函數。
3.NLSEF的數學模型
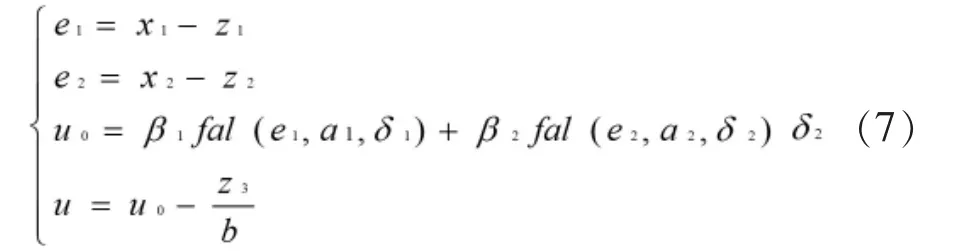
其中 α1,α2,β1,β2,δ1,為可調參數。
(三)無刷直流電機自抗擾控制系統設計
將無刷直流電機作為被控制對象,將自抗擾輸出信號u作為無刷直流電機的輸入。其基本結構如下所示。
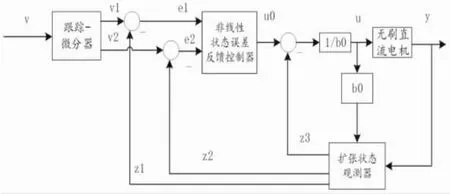
圖2 無刷直流電機系統框圖
當無刷直流電機的輸出信號y小于輸入信號v時,擴張狀態觀測器(ESO)觀測出正的誤差信號e,擴張狀態觀測器輸出的z1(t),z2(t)減小,而z3(t)增大。由于輸入信號v是不變的,誤差信號e1,e2以及u0會增大,u也會隨之增大,最終輸出信號y會增大。輸出信號y增大使誤差信號e減小,fal函數值大于零的區間也會減少,控制u的速度變慢。輸出信號的調節也變慢,反之當無刷直流電機的輸出信號y大于輸入信號v時,擴張狀態觀測器(ESO)觀測出負的誤差信號e,擴張狀態觀測器輸出的z1(t),z2(t)增大,而z3(t)減小。由于輸入信號v是不變的,誤差信號e1,e2以及u0會減小。u也減小,輸出信號v也會減小。輸出信號的減小會使誤差信號e增大,fal函數值小于零的區間也會增大,控制u的速度變快。輸出信號的調節也變快,經過上述調節,最終實現無刷直流電機的控制。
三、仿真模型的建立
在matlab中,借助于simulink環境下s函數,通過使用c語言或m語言將自抗擾的數學模型轉換成了離散算法,寫進s-function模塊中,設置好參數,得自抗擾控制的無刷直流電機控制系統的仿真模型如圖3所示。
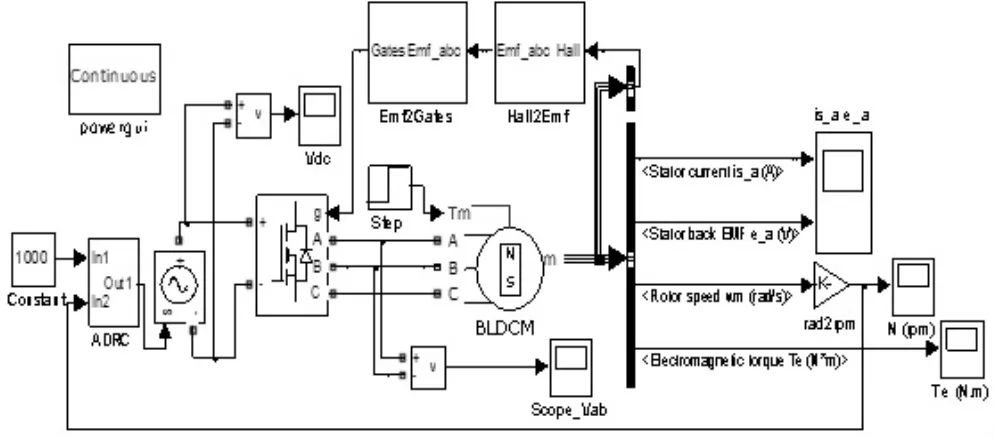
圖3 無刷直流電機自抗擾控制系統仿真模型
仿真過程中無刷直流直流電機參數設置如表1所示:

表1 電機參數
自抗擾控制器參數整定根據經驗法可得數據如表2所示:
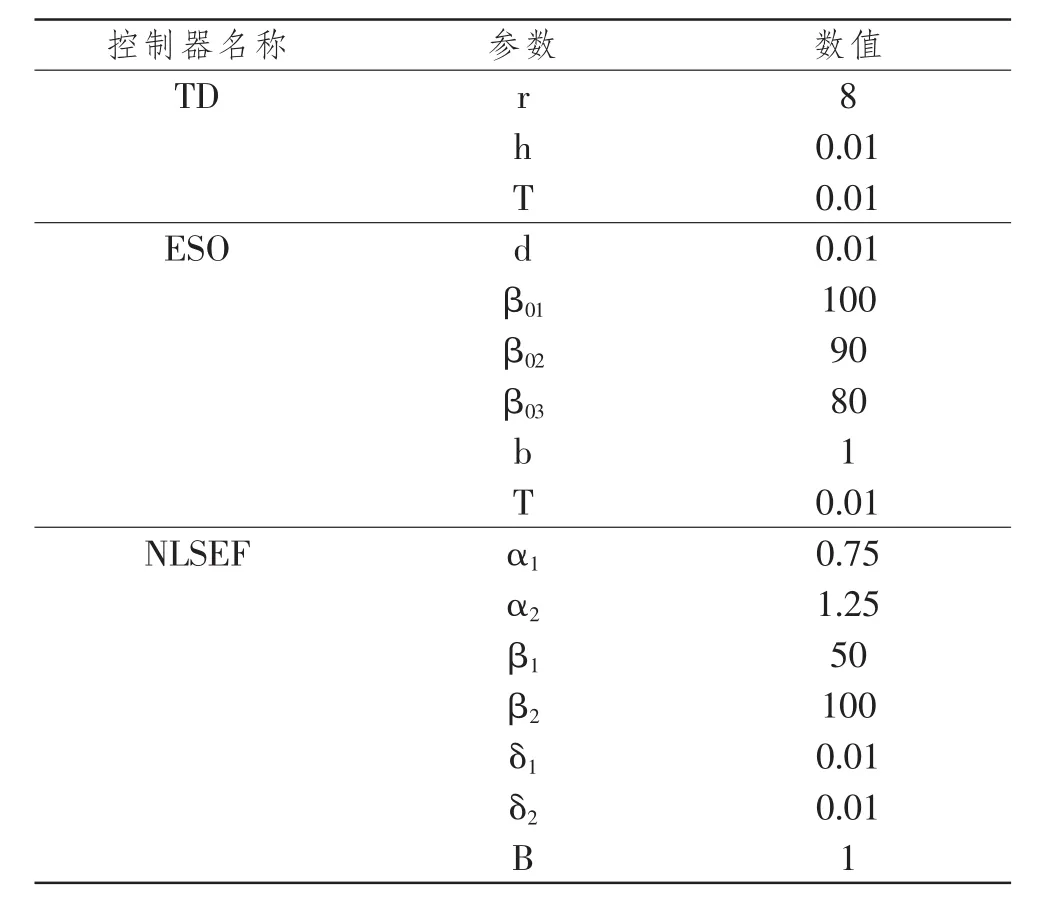
表2 自抗控制器參數
四、仿真結果及分析
(一)起動和突加負載實驗
無刷直流電機轉速的設定值為n=1000 r/min,在仿真時間t=0.1s時,給無刷直流電機加TL=1.5 N·m負載,然后分別對傳統PI控制和自抗擾控制下的無刷直流電機進行仿真實驗,得到無刷直流電機轉速仿真波形如圖4所示。
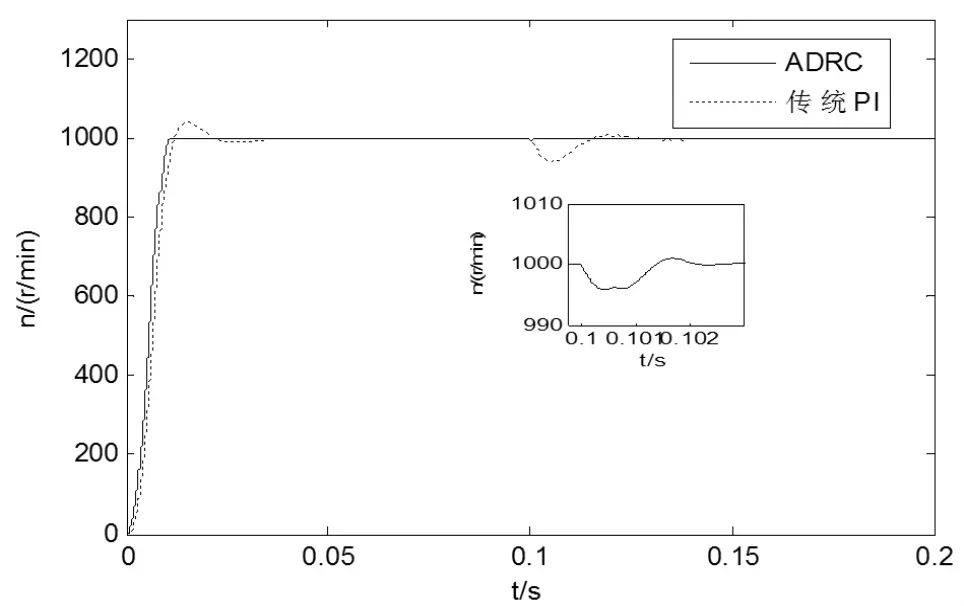
圖4 突加負載時轉速仿真圖形
圖(4)中內部圖形是ADRC曲線在0.1s時放大部分。由仿真波形圖可知,傳統的PI控制算法在t=0.05s時,無刷直流電機轉速達到穩定狀態,轉速最大時為1040r/min,超調為4%。而自抗擾控制算法在t=0.01s時無刷直流電機的轉速就已經穩定了,超調幾乎為0。系統在0.1s由于突加負載轉矩的作用,傳統PI控制在0.03s后轉速才能夠恢復,轉速最大下降到940r/min。超調為6%。而自抗繞控制在0.003s轉速就能恢復了,轉速下降到995r/min,超調僅為0.5%。
(二)改變速度給定實驗
無刷直流電機轉速設定值n=1000 r/min,在時間t=0.1s時,電機轉速由n=1000 r/min,突然下降為n=800 r/min,分別對傳統PI控制和自抗擾控制下的電機控制系統進行仿真實驗,得到電機的轉速仿真波形如圖5所示。
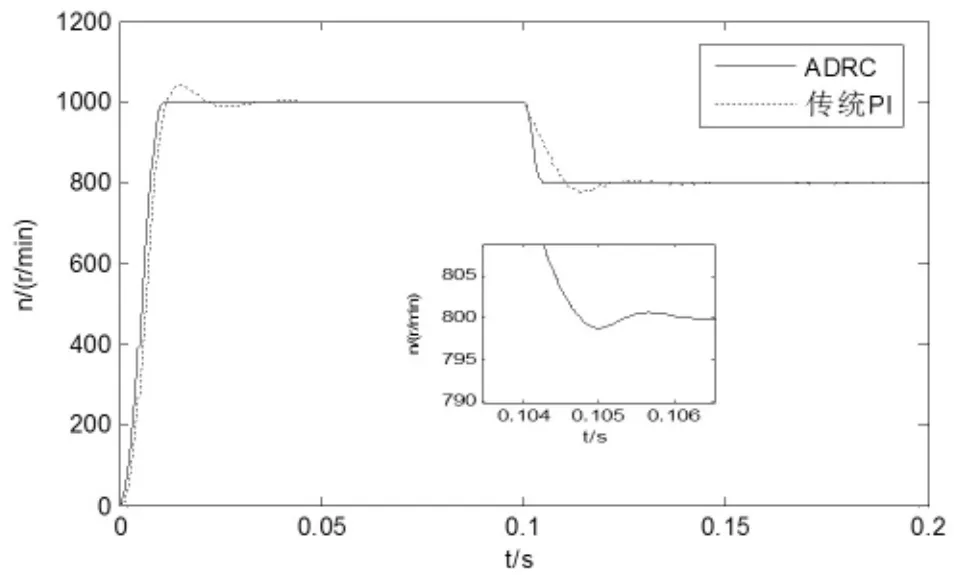
圖5 轉速突變時轉速仿真圖形
圖5中內部圖形是ADRC曲線在0.1s左右時放大部分。從圖中可知傳統PI控制在轉速突變時系統在t=0.025s后達到穩定,轉速下降到775r/min,超調為2.5%,而自抗擾控制在轉速突變時系統t=0.007就能夠穩定,轉速下降到798r/min超調0.2%。
通過仿真結果對比可以看出:
啟動時自抗擾制器比傳統PI控制器響應速度更快,調節時間更短,且無超調。突加負載或轉速突變時,自抗擾制器比傳統PI控制器不但具有較快的響應速度,而且對擾動適應性較強,魯棒性以及可操作性也非常好。
五、結論
針對傳統的PID算法控制下的無刷直流電機轉速抗干擾能力差、響應速度慢的問題,提出了采用自抗擾控制器來對無刷直流電機進行控制,搭建了無刷直流電機自抗擾控制的仿真模型,并與傳統的PID控制算法同時進行了對轉速控制的仿真實驗并分析對比,仿真實驗的結果表明:自抗擾控制器不但響應速度快,而且對擾動適應性較強,魯棒性以及可操作性也非常好。

