基于CFD/CSD耦合的全動平尾氣動彈性特性研究

羅文莉，陸琪

(上海飛機設計研究院，上海 201210)

0 引言

對于多數常規飛行器建模，采用適當的剛體假設是合理的。但是對于相對厚度較小的活動面，如水平尾翼來說，很容易出現氣動/結構耦合的現象，因此剛體假設是不可行的。尤其是隨著飛行速度的不斷增大，氣動彈性的影響已不容忽視。因此，對于全動平尾的氣動彈性研究是十分必要的。

關于氣動彈性問題的研究從20世紀50年代開始興起，由于計算能力的限制，那時的研究主要集中于風洞試驗以及非定常氣動理論。LAUTEN W T等[1]在氣動彈性方面對X-15的全動水平尾翼縮比模型進行了風洞試驗研究。基于活塞理論計算得到的顫振速度大約是試驗得到速度的4倍。HEEG J等[2]對6種全動尾翼模型進行了風洞試驗，主要針對翼型、翼軸剛度以及翼面質量分布進行了研究，全部試件的試驗顫振速度均低于使用2階活塞理論計算得到的值。

隨著計算能力的不斷提高，非定常氣動力的計算方法逐漸由依靠理論分析轉向了與CFD計算相結合的方法。MCNAMARA J J等[3-4]基于活塞理論、牛頓理論、激波膨脹波等非定常氣動力方法計算了一種雙楔形翼型的氣彈穩定性，并與基于求解N-S方程的CFD方法進行了對比，結果表明使用1階、2階活塞理論的誤差較大，并說明了黏性效應對于二維楔形薄翼型的影響基本可以忽略。

此后，集合了CFD流場分析和結構有限元計算(FEA)的CAE分析由于其在氣彈分析中的先進性成為了一股研究趨勢。MCNAMARA J J等[5]對X-33進行了氣動彈性分析，使用MSC.NASTRAN進行模態分析。GUPTA K K等[6]分別采用了基于活塞理論、CFD以及系統識別等方法計算非定常氣動力，結構采用有限元建模，得到的結果表明飛行器在工作環境中定常區域內不會發生顫振現象。

采用常規的理論算法或是基于CFD的非定常氣動力算法無法考慮翼型的變形。對于結構模型的求解，國內外大多理論方法均假設結構在靜變形平衡位置附近作小幅振動，采用線性結構振動方程，一些流固耦合降階方法也是基于線性考慮[7]。然而近年來，國外很多學者提出了HISSS/NASTRAN、CFL3D/GFEC、ZAERO/NASTRAN等CFD/CSD(Computational Fluid Dynamics/Computational Structural Dynamics) 耦合方法，開始將其應用在常規亞/超飛行器氣彈分析中。CFD采用精確的流動控制方程，CSD建立非線性結構模型，基于CFD/CSD耦合分析具有高精度，可用于復雜問題的研究。國內也有學者開展了相關研究，張華等[8]耦合FLUENT/NASTRAN，詳細研究了機翼結構彈性對氣動特性的影響，曾憲昂等[9]基于CFD/CSD耦合方法進行了某機翼的顫振分析。

1 計算方法

CFD/CSD耦合方法遵守基本守恒原則，在流體與固體耦合交界面處，滿足流體與固體應力、位移、溫度等變量的相等或守恒。通過分離解法分別求解流體和固體控制方程，再通過流固耦合交界面進行計算結果的傳遞。只要流固耦合面完全對應，可以保證交界面上的參數從局部到全局精確傳遞。由于各自的物理屬性，在進行數據傳遞時，并不是所有的變量都要進行傳遞。流體將力傳遞給固體，固體將位移傳遞給流體。使用動網格模擬流場形狀由于邊界運動而隨時間的改變，從而捕捉平尾的結構變形。

本文采用ANSYS軟件，CFD計算基于有限體積法求解非定常雷諾平均N-S(RANS)方程。采用標準k-ε湍流模型結合壁面函數法，選擇密度基隱式求解，對于空間離散方法，擴散項的無黏通量項選取AUSM通量差分分裂格式，而黏性通量項選取中心差分格式，對流項則使用2階迎風格式。時間積分使用高斯賽德爾(gauss-seidel)方法。CSD計算基于有限元法，對固體結構進行離散，將連續結構的無限維問題轉化為與節點位移相關聯的有限維問題。固體運動方程可由拉格朗日方程得到：

(1)

其中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；F為廣義力；x為節點位移向量。

2 建模

2.1 氣動模型

本文計算的全動平尾和坐標系定義如圖1所示，z軸垂直于x軸和y軸，按右手定則給定正方向。翼根弦長6.309m，平尾寬度2.22m，翼型相對厚度0.04m，翼面積15.52m2。

圖1 平尾平面形狀

計算域邊界采用pressure far-field條件，高度為30 km，壓力、溫度等氣體參數由標準大氣表查得。對平尾周圍流場進行網格劃分，如圖2所示。對稱面上采用對稱邊界條件，且在動網格設置中，對稱面設置為可變形面，將變形約束在面內。平尾上下表面、前后緣以及翼端面為設置流固耦合面，設置計算時間步長為0.001 s，最大迎角取40°。

圖2 平尾附近流場網格劃分

2.2 結構模型

采用直軸式全動平尾，即平尾與轉軸組成整體相對垂直于機身的轉軸旋轉。將轉軸位置定于翼根65%處，換算為平均氣動弦長的43%。蒙皮厚度取2mm，翼軸長度取1m。翼軸選擇TC4鈦合金材料，翼面蒙皮為鎳合金GH4169，平尾內部為全高度鎳合金蜂窩結構。對平尾結構進行網格劃分，如圖3所示，網格數為28 000。其中翼根處翼軸末端面固定，翼根面變形約束在面內，平尾上下表面、前后緣以及翼端面設置為流固耦合面。同樣設置時間步長為0.001 s。

圖3 平尾結構網格

對平尾進行模態分析，得到前4階模態如圖4所示，其中黑色線框表示未變形的平尾，云圖表示位移大小。各階模態、頻率見表1。

圖4 平尾模態分析

表1 模態頻率

3 氣彈特性分析

3.1 氣彈響應分析

分別計算平尾迎角為0°～40°間隔20°的情況，依次分析平尾的氣動參數以及結構參數響應，其中氣動參數包括升阻力系數，結構參數包括應力和平尾前緣點位移，初始值為不考慮結構彈性時的值。0°迎角時的氣彈響應如圖5所示。

圖5 0°迎角時的氣彈響應

可以看出升阻力系數均很快收斂，并無明顯波動。由于采用對稱翼型，0°迎角下升力系數為0，阻力系數也僅在10-4量級。考慮結構彈性之后升力系數幾乎不變，阻力系數增加30%，但幅值仍較小。結構響應結果同樣可以看出，應力和位移兩者均很快收斂穩定。其中最大應力值為0.42MPa，最大位移值為0.03mm，從量級上看，幾乎可以忽略。

圖6所示分別為20°和40°迎角下的氣動響應結果。可以看出，升阻力系數均出現波動，無相位差且呈收斂趨勢。20°迎角下升力系數初始值為0.282，收斂值約為0.272，減小約3.6%。阻力系數初始值為0.106，收斂值約為0.101，減小約4.7%。升阻力波動半衰時長約0.726 s。40°迎角下升力系數初始值為0.666，收斂值約為0.632，減小約5.1%。阻力系數初始值為0.563，收斂值約為0.526，減小約6.6%。升阻力波動半衰時長約0.478 s。

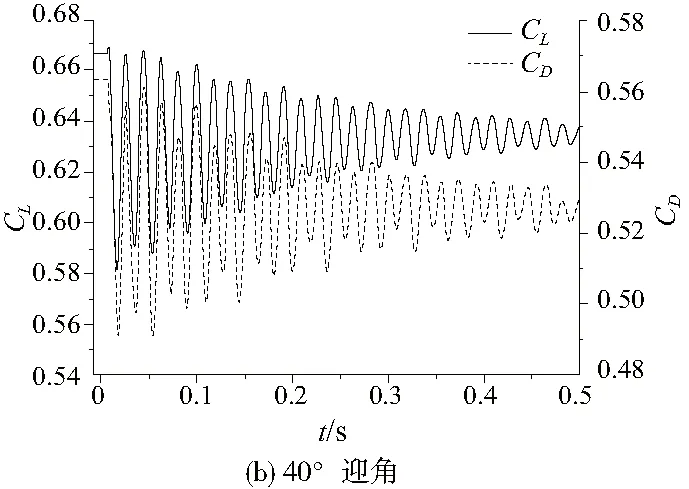
圖6 大迎角下的氣動響應

圖7所示分別為20°和40°迎角下的結構響應結果。可以看出20°迎角下平尾前緣點位移最大值約120mm，且隨時間逐漸衰減，收斂值約為60mm。在初始氣動載荷的作用下，結構的應力響應曲線迅速達到最大值，約115MPa。此后隨著時間的增長，響應逐漸衰減，最后收斂到約63MPa。40°迎角下位移最大值約330mm，且隨時間逐漸衰減，收斂值約為97mm。在初始氣動載荷的作用下，結構的應力響應曲線迅速達到最大值約320MPa，此后隨著時間的增長，響應逐漸衰減，最后收斂到約190MPa。

可見除0°迎角迅速收斂至平衡位置以外，在大迎角下平尾的升阻力系數以及前緣點位移、翼軸最大應力點等效應力曲線均出現波動，隨時間變化逐漸衰減至平衡位置。迎角越大，初始振幅越大，升阻力減小的比例越大，但衰減得越快。

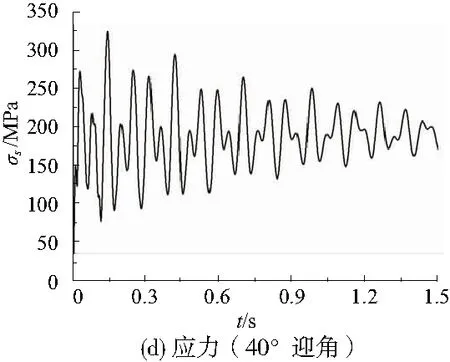
圖7 大迎角下的結構響應

3.2 流動特性分析

圖8所示為0°迎角下考慮結構彈性后翼根附近對稱面以及平尾上、下表面的壓力分布云圖。可在0°迎角下上下表面的壓力基本呈對稱分布，因此升力系數幾乎為0。

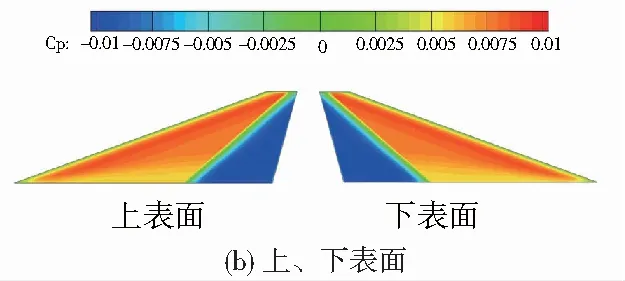
圖8 壓力分布云圖(0°迎角)

圖9所示為20°迎角時，初始流場與平衡位置所對應的平尾下表面壓力分布云圖以及平尾變形示意圖。可以看出，結構變形導致下表面的壓力分布發生變化。相比初始位置，平衡位置對應的平尾下表面后緣膨脹區低壓區域擴大，平尾前緣高壓區靠近前緣，使得翼尖處的高壓區域明顯縮小。

由平尾變形示意圖可以看出，平衡時平尾發生扭轉。從正視圖可以看出50%展長以內的部分前緣向上偏轉，相對迎角增大，從而使得激波偏折角增大，波后壓力增大，因此造成高壓區前移。而50%展長以外的部分前緣向下偏轉，相對迎角減小，相應的激波后壓力減小。從后視圖可以看出平尾后緣均向上偏轉，相對迎角增加，從而增大偏折角，但此時前方激波經過最大厚度處產生膨脹波，偏折角增大反而造成壓力減小。綜上，翼根前緣處壓力的增大無法彌補翼尖前緣以及整個平尾后緣壓力的降低，因此整體壓力減小，升力系數降低。

圖9 結構變形后的流場(20°迎角)

圖10給出了一個典型的振蕩周期內平尾結構變形以及表面壓力分布云圖的變化過程。取0.03s～0.08s，間隔0.01s的6個時刻。可以明顯看出平尾前緣扭轉和翼尖彎曲變形。變形最大時升力系數最小，對應地，變形最小時升力系數最大。

圖10 平尾結構變形和表面壓力分布云圖

3.3 結構特性分析

圖11所示為0°迎角時平尾的等效應力分布，可以看出，翼軸處應力分布較為集中，且應力最大出現在翼軸的x向與平尾相連接處。根據前文壓力分布特點可以得出0°迎角下平尾結構受到的力主要是阻力，集中在x軸方向，而在z向由于上、下表面對稱升力為0，因此應力較小。

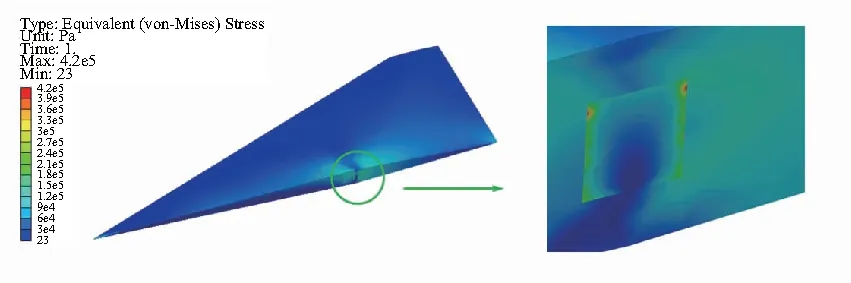
圖11 結構應力(0°迎角)

圖12為20°和40°迎角下變形最大時對應的等效應力分布云圖，可以看出，靠近翼軸處應力較為集中，而翼軸上的應力較小。迎角越大，最大應力越大。平尾內部最大應力在40°時達到1.9 GPa，已經達到所用鎳合金材料的

屈服強度極限，理論上說材料已經破壞，由于采用線彈性材料，計算結果可能較實際結果偏大，但為了保險起見，實際結構設計時應在翼軸與內部蜂窩接觸部位附近加固，防止蜂窩結構破壞。

圖12 大迎角下的等效應力分布云圖

4 結語

本文采用CFD/CSD流固耦合法對一種典型全動平尾進行了氣動彈性數值模擬。給出了不同迎角下平尾的氣動彈性響應，并分別針對流場和結構響應做出了分析，結果表明：

1) 除0°迎角迅速收斂至平衡位置以外，其余各迎角時的氣動力和結構響應曲線均出現波動，隨時間變化逐漸衰減至平衡位置。迎角越大，初始振幅越大，氣動力減小的比例越大，結構應力越大，但隨時間衰減得越快。

2) 結構變形導致下表面壓力分布發生變化。靠近翼根部分前緣上偏，壓力增大。靠近翼尖部分前緣下偏，壓力減小。后緣均上偏，壓力減小。整體壓力減小，升力系數降低。迎角越大，現象越明顯。

3) 靠近翼軸處應力較為集中，而翼軸上的應力較小。平尾存在彎曲/扭轉耦合現象，隨時間逐漸收斂至平衡位

置，但相對初始位置的變形隨迎角增大而增大。