二維材料熱傳導研究進展*

吳祥水 湯雯婷 徐象繁

(同濟大學物理科學與工程學院,聲子學與熱能科學中心,上海200092)

(2020年5月12日收到;2020年6月10日收到修改稿)

1 前 言

到目前為止,對于二維材料微納元器件的研究主要集中在其電學性質、機械性能以及光學性質.需要特別指出的是,對于任意微納元器件,不管是電子元器件還是光電元器件,散熱問題決定了該器件的工作性能及穩定性.高密度元器件在高速工作的過程中會產生大量熱量,如果不能及時將熱量疏導出去,就會導致元器件因局部溫度過高(即通常所說的熱點)而性能降低甚至被燒壞.如何將過多的熱量傳導出去,使得元器件在相對低溫環境下穩定運行是現代半導體工業面臨的普遍問題[1?5].所有的散熱過程都要通過一個重要的步驟:熱量通過微電子器件和散熱器之間形成的界面.大部分的微電子器件都是由半導體和金屬組成,所以半導體和金屬的接觸界面隨處可見.微電子器件的散熱問題涉及以下的物理問題:(1)熱量在微納尺度的材料里是如何傳輸的?(2)熱量是如何通過各種界面的?由于微納電子器件是半導體材料,而在半導體材料里聲子是熱量的主要載體.所以,以上所述問題變成了:(1)聲子如何在微納尺度半導體材料里傳輸?(2)聲子是如何透過各種界面?這兩個問題的研究是解決熱能轉換和高集成微納器件的散熱問題及熱能調控的關鍵.

近年來的研究結果表明在低維體系中聲子擴散是反常的.一維體系及二維系統中聲子的反常熱傳導已經是一個不需要爭辯的事實[6?9].有數值計算表明單壁碳納米管、硅納米線中的聲子輸運是反常的,其熱導率(k)不是常數,而是一個隨長度(L)發散的量:k-La[10];同時,二維材料的熱導率也是隨著長度發散的:k-logL[11,12].這一關系已經在碳納米管[13?16]、懸空單層石墨烯[17]和懸空單層/多層過渡金屬硫化物[18]的實驗中得到證實.因此,有大量的工作集中研究這種反常熱傳導和聲子擴散的物理機理[6?9,19];同時在研究界面熱導的過程中將這一反常行為考慮進去,嘗試去建立一個新的聲子界面熱輸運理論.

二維材料的發現為研究低維系統中聲子-聲子散射物理過程提供了一個絕佳的平臺。本綜述文章從微納尺度熱傳導實驗測量手段出發,介紹二維材料熱傳導在實驗方面的研究進展及相關物理問題,闡述二維材料-二維材料界面、二維材料-介電層之間的界面熱阻,并以此為出發點進一步解釋二維材料在散熱領域的應用前景.本文的內容安排如下:第2節介紹二維材料熱傳導測量技術;第3節介紹二維材料熱傳導研究進展及相關物理問題;第4節和第5節介紹二維材料之間界面熱阻、二維材料與介電襯底的界面熱阻調控及二維材料在散熱方面的研究進展;第6節為總結部分,并展望未來的研究方向與前景.

需要特別指出的是,除了石墨烯、氮化硼和黑磷等以外,通過元素周期表可以發現二維材料有一個極其龐大的家族[20].然而,目前的熱傳導研究只是涉及極少部分的二維材料,其原因可能是二維材料熱傳導測量存在很大的難度及技術瓶頸.本文希望通過對近十年來實驗工作的綜述,給讀者厘清二維材料熱傳導機理的基本物理圖像,并對其在散熱領域的應用起到一定的理論支持.

由于篇幅限制,本文只集中介紹二維材料熱傳導及界面熱阻調控相關基礎問題.已有很多關于低維材料熱學性質的文章可供參考,比如低維材料反常熱傳導[7?9]、二維材料熱傳導研究[6,21?26]、微納尺度熱傳導研究[27?29]等等.

2 二維材料熱傳導測量技術

在微納尺度的熱傳導測量方面,實驗方法一般包括兩種類型: 穩態測量(懸空熱橋法[30]、拉曼法[31]等)以及瞬態測量(3w法[32]、時域熱反射法[33]、激光脈沖熱測量法[34]等).下面將對一些常見測量方法的原理及發展進行簡要介紹.

2.1 懸空熱橋法

懸空熱橋法的發明得益于微納加工技術的飛速發展.由于在測量精度以及實驗操作難度上擁有較好的平衡,該方法已經成為微納尺度熱傳導測量的主流方法之一.2001年懸空熱橋法首次被用于微納尺度熱傳導測量,該實驗中所測量的樣品為單根多壁碳納米管[35].此前采用傳統方法只能測量一束納米線(納米管)的整體熱導率,而納米線(或納米管)之間的聲子散射導致無法精確得到單根樣品的熱導率[36].懸空熱橋法不僅可以測量微納尺度樣品的熱導率,還能同步測量樣品的電導率以及Seebeck系數,對于低維熱電材料的研究是比較適用的[37,38].

熱橋器件的制備流程是在硅晶片上進行一系列的光刻(或電子束曝光)、金屬沉積、腐蝕等操作[21,30].該測量器件主要由下列兩部分構成:(1)由厚度為300—500 nm的低應力氮化硅(SiNx)構成的兩個懸空平臺和連接懸空平臺與外部基底的六根懸臂,如圖1(a)中的藍色背底部分;(2)由厚度為50—100 nm的鉑/金等金屬構成的,位于懸空平臺、懸臂以及基底上的一系列電極,如圖1(a)中的黃色部分.

在實驗測量過程中,首先通過納米機械手轉移、濕法轉移、干法轉移或滴涂等方法將待測樣品轉移至兩個懸空平臺之間,然后在高真空腔體中進行測量(減小熱對流的影響).在進行測量時,將一個較大的直流電流(微安量級)和較小的交流電流(納安量級)通入某一側懸空平臺的電極中,并在另一側懸空平臺的電極中通入較小且大小相同的交流電流.其中,直流電流的作用是利用電極的焦耳熱效應充當熱源,電極電阻則通過交流電測得.在很小的溫度變化范圍內,金屬電極的電阻與溫度可近似為線性關系,因此可以利用電極電阻對懸空平臺的溫度進行標定.

假設通直流電流的懸空平臺上電極所產生的焦耳熱為Qh(Qh=I2×Rh,I為直流電流大小,Rh為電極電阻).兩根通直流電的懸臂電極所產生的焦耳熱為2QL,并可以假設其中一半熱量通過懸臂傳導至基底,另一半熱量則傳導至懸空平臺.其熱流圖如圖1(b)所示.通過上述測量過程,懸空材料熱導率可使用下述熱傳導模型計算得到[30]:

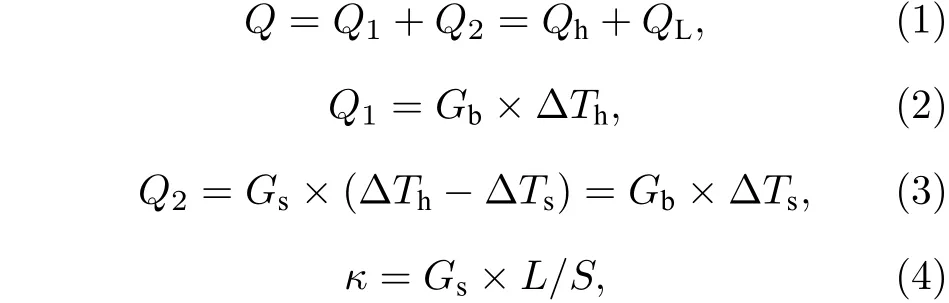
其中,Q表示通直流電流的懸空平臺上的總熱量;Q1表示通直流電流的懸空平臺一側,經六根懸臂所傳導至基底上的熱量;Q2表示經待測樣品所傳導的熱量;Gb、Gs分別表示六根懸臂的熱導和樣品的熱導;DTh、DTs分別表示通直流電流一側和另一側懸空平臺上的溫度變化,可由電極電阻與溫度之間的關系計算得到;k表示待測樣品的懸空熱導率;L、S分別表示待測樣品的長度和橫截面積.

根據上述原理,熱橋法用于測量低維材料熱導率存在一些問題:(1)(1)式成立的前提條件是假設連接懸空平臺與襯底的兩組懸臂的熱導(Gb)相同.然而,由于微納加工過程工藝的問題,兩組懸臂無法保持絕對一致,Gb之間的差別有時可高達10%,其結果是熱導率測量會出現偏差,甚至會出現偽熱整流效應[40].(2)懸空平臺的內阻問題.在計算樣品熱導(Gs)時所需要用到的是樣品與懸空平臺接觸部分的溫度,然而熱橋法實際測量的是懸空平臺的平均溫升(DTh和DTs).因此通常將懸空平臺的熱阻假設為無窮小,即假設懸空平臺內部不存在溫差,但是實際情況是兩個懸空平臺內部確實存在一定的內阻.因此,根據(3)式可知,對于熱導較低的樣品,該假設可近似成立.然而對于高熱導樣品(>5×10–8),如多層或者長度小于幾百納米的石墨烯和氮化硼等,需要用有限元分析對測量結果進行修正[41,42].(3)兩個懸空平臺之間存在一定的熱輻射,其值在室溫下約為10–10—10–11W/K,因此在測量低熱導樣品時(如有機納米線,無定性納米線等)需要去除熱輻射的影響[39].

近年來懸空熱橋法已成功應用于石墨烯[17,43]、氮化硼[41,44]、硫化鉬[45?47]、黑磷[48,49]等二維材料的熱導率測量.雖然懸空熱橋法的測量精度相較于下述拉曼法(2.3節)有比較明顯的優勢,但是仍然有一些問題值得注意.首先,樣品轉移的過程中,傳統的濕法轉移方法會在樣品表面引入大量有機物殘留,嚴重影響測量結果[43].為了解決這一難題,科研人員開發了干法轉移[41]以及酒精輔助機械手轉移[46]等多種轉移方法.其次,待測樣品的熱阻(Rs=1/Gs)不僅包含了樣品的本征熱阻(Rin),還包括樣品與懸空平臺之間的接觸熱阻(Rc):Rs=Rin+2Rc,如圖1(c)所示.在某些實驗中,上述接觸熱阻占實驗所得到的總熱阻的比例可達到30%—40%,甚至更高[41,50],因此僅僅根據上述數據處理方法所得到的結果存在嚴重的誤差.在接觸點沉積金屬(金、鉑等),可以在一定程度上改善接觸狀態,降低接觸熱阻的影響[17,51].此外,截距法[45]與接觸熱阻計算[43]是目前解決該問題最常見的兩種方法.除了上述兩個問題以外,普通的懸空熱橋法測量系統對測量低熱導的樣品(非晶材料、有機物等)是非常棘手的.由于測量過程中懸空平臺的溫度變化會非常小,信噪比太低,樣品信號容易淹沒在環境溫漂中.但是近年來對微納尺度低熱導材料的熱傳導性質測量的需求非常強烈,因此針對測量系統進行改良所開發的惠斯通電橋法[52]以及比較器法[39]便應運而出,如圖1(d)所示.同濟大學徐象繁課題組[39]利用比較器法測量了單根聚酰亞胺納米纖維的熱導率, 該實驗中樣品熱導約為1.0 ×10–10W/K,比普通熱橋法所能測量的下限低一個數量級,由此可見該方法的使用極大的拓寬了熱橋法的使用范圍.Zheng等[53]采用交流加熱法消除白噪聲,可進一步將測量精度提升至約0.25 pW/K.

2.2 電子束自加熱法

在上述懸空熱橋法中,樣品與懸空平臺之間的接觸熱阻是該方法的主要缺陷之一.雖然已經有一些方法可以對其進行改善,但是終究無法從實驗原理上消除該缺陷的影響.2010年新加坡國立大學John Thong課題組和李保文課題組共同開發了一種基于懸空熱橋法的新型測量方法——電子束自加熱法[42,54].該方法不僅可以從原理上消除樣品與懸空平臺之間的接觸熱阻對實驗結果的影響,而且還能夠測量微納尺度異質結材料熱阻的空間分布(懸空熱橋法只能對樣品整體的熱阻進行測量).電子束自加熱法的測量過程是在掃描電子顯微鏡(SEM)中完成的.利用SEM中的高能電子束與樣品之間的相互作用充當熱源,并且電子束(熱源)可以在樣品上連續掃描(移動),如圖2(a)所示.

假設電子束掃描的位置坐標為x,該處樣品的溫度變化為DTi(x),同時熱量將從掃描處往兩側傳導,引起兩端懸空平臺的溫度變化分別為DTL(左側),DTR(右側).熱量會通過六根懸臂傳導至基底上,基底溫度為T0,熱流如圖2(b)所示.建立熱傳導平衡方程為[55]

其中,Ri(x)表示從掃描處至樣品左端的樣品熱阻,Rb表示六根懸臂的總熱阻,Rs表示樣品整體熱阻(包括樣品與懸空平臺的接觸熱阻).

圖2電子束自加熱法[54](a)示意圖;(b)熱流圖;(c)同濟大學測量裝置圖;(d)利用電子束自加熱法測量多層硫化鉬的熱導率Fig.2.The electron-beam self-heating method [54]:(a)Sketch;(b)heat flow of device;(c)experimental setup in Tongji University;(d)measuring thermal conductivity of few-layer MoS2.

在同一個樣品中,利用懸空熱橋法測量,左側懸空平臺為加熱端,可測得左側與右側懸空平臺溫度變化分別為DTL0和DTR0.結合上式以及懸空熱橋法測量原理,可得

其中,ai(x)表示DTL/DTR,a0表示DTL0/DTR0,Rb可由懸空熱橋法測得.通過上述測量過程可得到Ri(x)與位置x之間關系,同時如果已知樣品的橫截面積(A),則樣品熱導率可表示為

通過分析可知,采用電子束自加熱法測量樣品熱導率是不會受到接觸熱阻影響的.同濟大學徐象繁課題組搭建了國內首臺電子束自加熱法的測量裝置,并將該方法應用于多層硫化鉬的室溫熱導率的測量[54],如圖2(c)和2(d)所示.雖然電子束自加熱法的優點很明顯,但是同樣不可忽視其缺點,例如尚不能進行變溫測量、不能測量對電子束敏感的材料,且對樣品表面雜質非常敏感(有機物等).

2.3 拉曼法

2008年首次實驗測量二維材料——單層石墨烯的懸空面內熱導率所使用的方法便是拉曼法[31].自此,拉曼法逐漸成為二維材料熱傳導領域中重要的實驗測量方法,并已成功應用于氮化硼[56,57]、黑磷[58]、硫化鉬[18,59,60]等多種二維材料的熱導率測量.拉曼法測量二維材料熱導率的原理主要基于以下兩點:(1)二維材料對拉曼激光具有一定的吸收作用,因此拉曼激光可以作為熱源;(2)二維材料的拉曼光譜吸收峰位置與溫度存在一定的線性關系[58,61,62],因此可以利用材料的拉曼光譜確定其表面溫度.結合以上兩點原理,并通過熱傳導模型計算,即可得到二維材料的熱導率.

拉曼法測量二維材料熱導率的原理圖如圖3(a)所示.假設熱傳導模型為圓形,該二維材料的熱導率可表示為[31]

其中,h表示該二維材料的厚度;dP表示該二維材料所吸收的拉曼激光能量,dT表示該二維材料的表面溫度變化.

實驗中可測得該材料拉曼吸收峰與表面溫度的關系,通過線性擬合可得到:

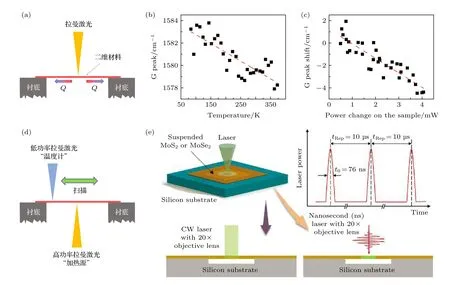
圖3(a)拉曼法測量原理圖;(b)(c)單層懸空石墨烯拉曼G峰頻率與溫度以及激光能量的關系[31,61];(d)雙拉曼法示意圖[67];(e)ET-Raman法示意圖[70]Fig.3.(a)Sketch of the Raman method;(b),(c)experimental data for the Raman G peak shift with respect to temperature and laser power[31,61];(d),(e)sketch of the Two-Raman method[67]and ET-Raman method[70].

其中,w表示材料表面溫度為T時,拉曼吸收峰的頻率;w0表示該材料在0 K時,拉曼吸收峰的頻率;e表示拉曼吸收峰頻率變化與溫度變化的比值常數.結合上述公式,可得

因此,實驗中只需測量不同溫度以及不同拉曼激光功率下,材料吸收峰的位置變化,即可得到該二維材料的熱導率,例如石墨烯拉曼G峰位置與溫度以及所吸收激光能量之間的關系[31,61],如圖3(b)和圖3(c)所示.

以上模型只針對圓形(corbino)樣品.矩形、一維樣品測量原理一樣,但其熱導模型略有不同,可查閱相關文獻.

通過上述分析,可以看出使用拉曼法測量二維材料熱導率是可行且有效的,但是在實際測量中卻存在一些不可忽視的問題.首先,在早期的幾個實驗中準確測量材料對拉曼激光的吸收功率存在一定難度,其所影響的實驗結果不確定度能達到30%— 50%[24].例如,在不同文獻中所使用的懸空單層石墨烯對拉曼激光的吸收率數值差別非常大(2.3%—13%),導致所得到的懸空單層石墨烯面內熱導率存 在 較 大 差 異(5300—630 W/(m·K),T=300 K)[31,63].其次,利用拉曼光譜吸收峰位置變化確定材料表面的溫度,其精度較低(8—40 K),嚴重影響測量結果的精確性[31,64].另外,因為其較低的溫度測量精度,使得拉曼法測量通常會將樣品的溫度加熱幾十度甚至一兩百度,導致測量結果有嚴重偏差.如Geim等[63]測量懸空單層石墨烯熱導率約為630 W/(m·K),實驗中他們發現雖然襯底溫度保持T=295 K,但是在功率為6.2 mW的激光加熱情況下懸空石墨烯中間位置溫度達到了約660 K.除了上述技術難點以外,襯底對激光的反射、非懸空二維材料的熱導率(材料與襯底接觸部分)、拉曼激光光斑尺寸、二維材料與襯底之間的接觸熱阻等未知因素同樣會對測量結果產生一定影響[65].

為了針對部分上述問題進行改良,科研人員通過改進實驗設備或計算模型,在提高拉曼法的測量精確度上有了一定的突破. 例如, 2010年蔡偉偉等[66]利用激光功率計同步測量單層石墨烯對拉曼激光的吸收率,并且在計算模型中加入了襯底的影響,一定程度上提高了測量結果的精確性.2014年Reparaz等[67]開發出一種雙拉曼激光的測量方法,其中一束高功率激光作為固定加熱源,另一束低功率激光掃描二維材料懸空部分,并通過拉曼吸收譜得到懸空部分的溫度場分布.該方法的優點在于可以排除襯底對測量結果的影響,如圖3(d)所示.2016年清華大學張興課題組[68,69]結合連續激光與脈沖方波激光,通過改變光斑半徑以及脈沖激光周期,能夠在無需知道二維材料對拉曼激光的吸收率的情況下得到材料的熱導率.同年,愛荷華州立大學王信偉課題組[70]引入一種新型拉曼技術(ETRaman),該方法不僅不需要獲得二維材料對拉曼激光的吸收率同時無需利用拉曼吸收峰對材料表面進行溫度標定,如圖3(e)所示.隨著拉曼法的不斷發展與完善,其已逐漸成為一種微納尺度熱傳導測量的成熟方法[71].

2.4 時域熱反射法

1983年Eesley將皮秒級脈沖激光應用于探測金屬銅中的非平衡熱輸運過程[72],自此時域熱反射法(time-domain thermoreflectance,TDTR)正式被應用于材料熱物性的測量.經過30多年的發展,TDTR已經成為一種被廣泛使用的材料熱物性非穩態測量方法,通常應用于測量塊材或薄膜的熱導率以及界面熱阻[73?75].其基本原理為:將一束飛秒級脈沖激光通過分光鏡分為泵浦光及探測光,其中泵浦光充當熱源對材料表面進行加熱,而探測光用于測量材料表面溫度的變化(材料表面對激光的反射率與溫度有關).通過位移平臺可以精準控制兩束光之間的光程差,進而控制它們到達材料表面的時間間隔,產生一定的時間延遲(td),由此可以測量從加熱到恢復環境溫度過程中,材料表面溫度隨延遲時間的變化,該溫度的變化過程與材料熱物性有關.

TDTR的測量系統包括飛秒激光發生器、分光器、位移平臺、電光(聲光)調制器、光電二極管探測器、鎖相放大器等[33],如圖4(a)所示.在測量之前,一般需要在待測樣品表面鍍一層金屬薄膜作為傳感層,因為在很小溫升情況下金屬表面對激光的反射率與溫度之間近似呈線性關系,能夠更加精確地標定其表面溫度.通過上述測量過程,鎖相放大器將輸出基于調制頻率的同相信號(Vin)和反相信號(Vout),該信號中包含了樣品表面溫度變化的信息,隨之可以得到同相信號與反相信號之比(Vin/Vout)與延遲時間之間的關系,如圖4(b)和圖4(c)所示,最終通過建立熱傳導模型并擬合實驗數據即可得到樣品熱物性的相關數據.TDTR已被適用于測量石墨烯[76]、黑磷[77]、硫化鉬[74,75]、硒化鎢[78]等二維材料的熱物性.

圖4 (a)時域熱反射法測量系統;(b)經正弦調制的飛秒脈沖激光、材料表面溫度響應、鎖相放大器所輸出的同相信號和反相信號與延遲時間之間的關系;(c)采用時域熱反射法測量GaN熱導率及Al/GaN界面熱導[33]Fig.4.(a)Experimental setup of the TDTR method;(b)femtosecond pulse laser with sinusoidal modulation,temperature response of sample surface,the in-phase signal and out-of-phase signal of Lock-in Amplifier versus delay-time;(c)using TDTR method to measure thermal conductivity of GaN and interface thermal conductance of Al/GaN[33].

與穩態熱測量方法相比,TDTR無需在真空腔體中進行測量,其次它可以用于超快熱輸運機理研究(電聲相互作用等).但是其缺點也是比較明顯的,例如該方法對樣品表面的光滑程度要求比較高,一般需要表面粗糙度小于15 nm.其次,測量之前需要在樣品表面沉積幾十個納米的金屬薄膜用作傳感層.然而很多二維材料,特別是單層或者多層二維材料,其表面吸附雜質或者沉積物會抑制面外聲學聲子,導致該方法無法準確測量單層/多層二維材料的本征熱導率[79].這點我們會在本文后續進行詳細討論.近年來,經過不斷的改進與發展,在TDTR的基礎之上已衍生出頻域熱反射法(frequency-domain thermoreflectance,FTDR)[80]以及結合time-resolved magneto-optic Kerr effect(TR-MOKE)[81]、asynchronous optical sampling(ASOPS)[82]等技術提高TDTR的測量精度或擴大其適用范圍.

2.5 其他微納尺度熱傳導測量方法

除了上述三種方法以外,微納尺度熱傳導的測量方法還包括:(1)瞬態測量3w法[32,83,84].該方法對樣品的厚度有一定的要求,因此通常用于測量塊材或薄膜的面間熱導率或接觸熱阻;(2)基于原子力顯微鏡(atomic force microscope,AFM)改裝的熱探針掃描法(scanning thermal microscopy,SThM)[85?87],該方法可提供材料納米尺度的熱阻分布圖像;(3)T-bridge法[88]、懸空Four-Point熱測量法[89]、激光脈沖熱測量法[34]、薄膜自加熱法[90]等.

上述方法均有各自的優缺點,在實際測量中需根據材料特性以及實驗設備酌情選擇.欲進一步了解各測量方法的細節情況,可查閱相關文獻[6,21,23,91?93].

3 二維材料熱傳導研究進展

3.1 各種二維材料的熱傳導性質

3.1.1 石墨烯

石墨烯作為第一種被成功制備的二維材料,一經發現便成為科研界的“寵兒”.其擁有一系列優異的物理性質—狄拉克錐能帶、超高電導率、超高載流子遷移率等[94?96].在熱傳導方面,石墨烯同樣表現出色,其室溫本征熱導率能達到2000—3000 W/(m·K),是迄今為止發現的熱導率最高的材料.2008年,Balandin等[31]通過拉曼法首次測量了室溫環境中懸空單層石墨烯的熱導率,測量結果顯示其熱導率遠高于金剛石(當時已知熱導率最高的材料)和石墨塊材, 達到4840—5300 W/(m·K);然而隨著科研人員進一步的研究,發現該實驗對石墨烯的拉曼激光吸收功率可能存在過大的估計,導致結果偏大4—6倍[31,97].2010年,蔡偉偉等[66]采用同樣的方法測量了懸空單層石墨烯的熱導率,并同步使用激光功率計測量了石墨烯的拉曼激光吸收率,結果顯示化學氣相沉積法(CVD)所生長的單層石墨烯的熱導率約為2500—3100 W/(m·K)(T=350 K)和1200—1400 W/(m·K)(T=500 K),并發現石墨烯懸空部分的形狀、尺寸和測量環境(空氣、真空等)對最終的結果會產生一定的影響.除了激光吸收率存在爭議以外,造成不同實驗結果之間存在較大差異的另一主要原因是石墨烯的制備方式不同(機械剝離或化學氣相沉積法),導致其品質(雜質、晶界、有機物殘留等)存在一定的差別,這些因素會對聲子產生額外的散射.表1中列舉了包括拉曼法在內的不同實驗方法所測量的懸空單層/多層石墨烯的熱導率.

為了進一步理解石墨烯中超高熱導率的物理機制,了解不同聲子模式對熱導率的貢獻是至關重要的.在石墨烯中,熱量主要通過聲學聲子傳輸,其聲學聲子模式包括面內聲學縱波(LA)、面內聲學橫波(TA)—與波矢q之間呈線性關系,以及面外聲學橫波(ZA)—與波矢q之間呈平方關系.Nika等[101]認為單層石墨烯中熱輸運過程幾乎全部由LA/TA聲子模承擔,而ZA聲子模對熱導率的貢獻可以忽略不計,這主要是因為當波矢q較小時ZA聲子的群速度將趨近于零,而且面外方向的Grüneisen常數比較大.但是,Lindsay等[102,103]認為ZA聲子模具有比較大的低頻聲子態密度,因而其對熱導率的貢獻會比較大,并預測室溫下ZA聲子模對單層石墨烯熱導率的貢獻能達到約70%,如圖5(a)所示.同時提出在低溫下,LA/TA聲子模與ZA聲子模所引起的熱導率與溫度之間分別呈k-T2和κ-T1.5的關系.將兩者貢獻加在一起之后, 低溫熱導率與溫度之間的關系約為κ-T1.68.除了超高熱導率以外,石墨烯同樣是研究聲子彈道輸運的絕佳平臺.由于石墨烯中聲子的平均自由程非常長,室溫下能達到微米量級,因此可以通過調節石墨烯帶的長度與寬度研究聲子的(準)彈道輸運性質[104].2010年徐象繁等首次使用懸空熱橋法測量了單層CVD石墨烯納米帶(寬度約3μm,長度約500 nm)的熱導率,發現在低溫區(T<140 K)熱導率與溫度之間成一定的指數關系(κ-T1.53±0.18),由此可以說明在單層懸空石墨烯中熱輸運主要依賴于ZA聲子模,同時發現了聲子的準彈道輸運的實驗證據[17,100],如圖5(b)所示.雖然Petters等[43]對上述實驗中測得的低熱導率(約225 W/(m·K))提出異議,認為觀測到的k~T1.53±0.18并非來自ZA聲子而是由于樣品表面存在的雜質.然而,當聲子存在彈道輸運時,熱導率并非樣品本征物理量,因為其會隨著長度的增加線性增加.在這種情況下,用單位面積的熱導s/S(s表示為樣品熱導,S表示為樣品橫截面積)來表達樣品的熱傳輸性質會更加準確.該實驗在低溫下觀測到的s/S已接近40%-50%的聲子彈道輸運理論極限[105]s/S≈[1/(4.4×105T1.68)+1/(1.2×1010)]–1W/(m2·K),表明該批樣品表面無雜質且可以提供充足證據證明ZA聲子的主要貢獻.

表1不同文獻中測量懸空石墨烯熱導率實驗細節Table 1.Experimental detail of thermal conductivity in suspended single/few-layer graphene from different literature.

圖5(a) 懸空單層石墨烯中各聲子模式貢獻熱導率比例[102];(b)實驗觀測單層懸空石墨烯中聲子的(準)彈道輸運[17,35,111]Fig.5.(a)Phonon modes contribution to thermal conductivity in suspended single-layer graphene[102];(b)experimental observation of(quasi-)ballistic phonon transport in suspended single-layer graphene[17,35,111].

以上討論的熱導率理論是基于三聲子散射模型計算.四聲子散射往往被直接忽略,因為其是只有在高溫區才會逐漸出現的一類聲子散射行為[106].但是近年理論研究發現即使是在室溫環境下,單層石墨烯中大量的低能ZA模聲子導致其四聲子散射過程是不容忽視的,因此此前只使用三聲子散射模型計算的單層石墨烯熱導率可能是偏高的[107,108].通過求解玻爾茲曼方程并引入四聲子散射,Feng等[107]發現室溫下單層石墨烯的熱導率僅為810 W/(m·K),該數值遠低于僅包含三聲子散射的計算結果(約3383 W/(m·K)),同時結果顯示在四聲子散射的影響下ZA聲子模對熱導率的貢獻也僅為31%.該工作在計算室溫下單層石墨烯熱導率的過程中所使用的原子力常數為0 K值.隨后上海交通大學顧驍坤等[108]對上述結果進行修正,所得到的結果數值相較上述文獻稍大,進一步證實了室溫下四聲子散射對單層石墨烯熱導率的嚴重影響.

由此可見,單層懸空石墨烯的熱導率值到底是多少仍未有定論.這個問題不管是在理論還是實驗上都存在一定的爭議.

在實際應用中,石墨烯更可能是附于某一襯底上.因此除了懸空石墨烯以外,研究襯底上石墨烯的面內熱傳導性能也是必要的.Seol等[103]測量了氧化硅襯底上單層石墨烯的面內熱導率(約600 W/(m·K),300 K).當石墨烯附于襯底上時,ZA聲子模將會被抑制,因而其面內熱導率比懸空石墨烯低.如上述理論計算結果所示室溫下ZA聲子對熱導率的貢獻能達到約70%,但是當存在襯底時ZA聲子模的貢獻將被嚴重抑制甚至消失,熱導率數值將從~3000 W/(m·K)降至~600 W/(m·K).該實驗有效驗證了石墨烯中ZA聲子對其熱導率起主要貢獻.除了氧化硅以外,氮化硅也是一種常見的襯底材料,Thong等[42]測量了氮化硅襯底上多層石墨烯的面內熱導率,其數值為~150—1250 W/(m·K)(室溫).為進一步驗證ZA聲子對熱導率的貢獻.Wang等[109]將金原子沉積到懸空三層石墨烯表面,發現其熱導率從約1500 W/(m·K)降至約270 W/(m·K),降幅達82%,得到了與Seol等一樣的結論.Jang等[110]研究了SiO2-石墨烯-SiO2三明治結構熱輸運性質,發現熱導率會進一步降低;特別是單層三明治結構石墨烯,其室溫熱導率遠低于160 W/(m·K)(該文中具體數值過低無法測出,只給了一個上限),表明襯底對石墨烯的熱導率有著非常顯著的抑制作用.

相較面內熱導率而言,石墨烯面間熱導率的研究是較少的.石墨烯的層間作用力屬于較弱的范德瓦爾斯力,因此最初普遍認為石墨烯的面間聲子平均自由程非常短(幾個納米). 但是2012年Harb等[112]測量了厚度為35 nm的石墨烯的面間熱導率(約0.7 W/(m·K),T=300 K),比塊材石墨的面間熱導率(約7 W/(m·K),T=300 K)低一個數量級,因此他們認為該現象的出現可能是由于之前對石墨烯的面間聲子平均自由程的估計偏小.隨后東南大學陳云飛課題組[113]通過分子動力學模擬發現石墨烯的面間聲子自由程能達到數微米,遠超出之前的理解.2015年Fu等[114]測量了不同厚度的石墨烯(24 nm—714 nm)的室溫面間熱導率,發現隨著厚度增加石墨烯的面間熱導率逐漸變大,同時熱導率的數值未觀測到一個飽和閾值, 他們認為石墨烯的面間聲子自由程能夠達到200 nm. 此后, Minnich等[115]進一步測量了厚度為(24 nm—21.9μm)的石墨烯/石墨薄片的面間熱導率,結果顯示在低溫區(高溫區)面間熱導率直到厚度約為2 μm(800 nm)才達到飽和閾值,并接近石墨塊材的面間熱導率.因此他們認為石墨烯的面間聲子自由程至少為40—250 nm(室溫)和100—600 nm(低溫),如圖6所示.

圖6 實驗測量石墨面間熱導率與厚度的關系[112,114,115]Fig.6.out-of-plane thermal conductivity of graphite versus thickness in experiment[112,114,115].

3.1.2 氮化硼

因帶隙較大(5.5—6.0 eV)且表面非常光滑,氮化硼(h-BN)是非常理想的一類介電材料.同時氮化硼塊材的熱導率(約400 W/(m·K),室溫)與銅很接近,且相同體積下其質量比銅低很多,因此在電子器件散熱的方面擁有廣闊的應用前景[116,117].

氮化硼被稱為白色石墨烯,其晶體結構與石墨烯類似.其面內氮原子與硼原子相互交錯形成蜂窩狀結構,層間依靠范德瓦爾斯力相互結合,屬于較早被發現的二維材料之一[118].由于擁有相似的晶體結構,氮化硼與石墨烯的物理性質也就具有一定的相似之處.Lindsay等[119]通過求解玻爾茲曼方程的理論研究,預測單層氮化硼的室溫面內熱導率為600 W/(m·K),高于氮化硼塊材,同時還發現其面外ZA聲子模對熱導率貢獻能達到~60%.

2013年Jo等[120]采用微橋電阻溫度計法測量了多層氮化硼的懸空面內熱導率(250 W/(m·K),5層;360 W/(m·K),11層;T=300 K).他們認為之所以測量數據較理論預測偏低,甚至比氮化硼塊材熱導率低,主要是因為在實驗過程中氮化硼表面存在大量有機物殘留導致聲子散射嚴重.在后續的多層氮化硼懸空面內熱導率的實驗中均未觀察到熱導率超過其塊材,其中樣品的質量是關鍵因素[57,62,121].直到2016年同濟大學徐象繁課題組[41]通過改善樣品轉移方法——PDMS輔助干法轉移使得氮化硼薄膜表面有機殘留大大減少.同時他們使用質量較高的塊材機械剝離制備多層氮化硼,首次測得懸空雙層氮化硼的熱導率較塊材高,室溫下達到460—625 W/(m·K).隨后,迪肯大學李璐華等[56]使用拉曼法測量了室溫附近單層/雙層以及三層懸空氮化硼的熱導率,隨著厚度增加熱導率數值會有所降低,但是均高于塊材氮化硼熱導率,其中單層氮化硼的熱導率達到~751 W/(m·K),是迄今為止實驗上得到的單層/多層氮化硼熱導率的最高值.表2中列舉了不同文獻中測得的懸空氮化硼面內熱導率.從表中數據可以看出,采用機械剝離方法制備的多層氮化硼熱導率普遍高于采用CVD方法制備的多層氮化硼,其中原因是由于化學氣相沉積法往往會在樣品中引入較多的缺陷,而機械剝離法在控制樣品質量方面則表現得更好一些.

表 2不同實驗中懸空單層/多層h-BN熱導率實驗測量細節表Table 2.Experimental detail of thermal conductivity of suspended single/few-layer h-BN in different literature.

3.1.3 硫化鉬及其他過渡金屬硫化物

過渡金屬硫化物(MX2,其中M代表Mo,W,Ti等過渡金屬元素,X代表硫族元素,包括S,Se,Te)是非常重要的一族二維材料,它們的晶體結構屬于“三明治”型層狀結構[122].與單層石墨烯、單層氮化硼等只包含一個原子層的二維材料不同,單層過渡金屬硫化物包含三個原子層——過渡金屬原子層被硫族元素原子層“夾”在中間[123],如圖7(a)所示.

硫化鉬是被研究的最為廣泛的一種過渡金屬硫化物,因帶隙可控且電學性質優良,同時能夠在空氣中穩定存在,被認為是極具潛力的下一代微電子器件材料,并且在光學、熱電等領域同樣存在一定的應用前景[122,124,125].2013年Sahoo等[59]使用拉曼法測量了11層硫化鉬的懸空面內熱導率(約52 W/(m·K),室溫).隨后,Yan等[60]和Jo等[126]分別測量了室溫下單層以及多層硫化鉬的懸空面內熱導率,其數值為35—52 W/(m·K).但是2015年Hone等[127]同樣采用拉曼法測量單層/雙層硫化鉬的懸空面內熱導率, 其結果(77—84 W/(m·K))遠大于之前實驗的數據,他們認為主要是由于實驗中所得到的硫化鉬的拉曼峰頻率變化與溫度關系、拉曼激光吸收功率以及接觸熱阻等關鍵數據均與之前的文獻存在較大差異.2018年同濟大學徐象繁課題組[54]使用電子束自加熱法測量了多層硫化鉬的懸空面內熱導率,這是首次將該方法應用于實驗測量二維材料的熱導率,實驗結果也證實了該方法的可行性.表3中列舉了不同文獻中硫化鉬面內熱導率的實驗測量結果.

圖7 晶體結構(a)硫化鉬[123];(b)黑磷[48];(c)塊體碲[150]Fig.7.crystal structure of(a)MoS2[123],(b)BP[48],(c)bulk Te [150].

表3不同文獻中硫化鉬單層/多層熱導率實驗測量細節表Table 3.Experimental detail of thermal conductivity of single/few-layer MoS2 in different literature.

硫化鉬的晶體結構相較石墨烯以及氮化硼存在一定的差異,因此其熱傳導性質也會有所不同,主要體現如下:首先單層硫化鉬的熱導率較單層石墨烯和單層氮化硼低1—2數量級.新加坡高性能計算研究所張剛課題組[130]通過理論計算發現單層硫化鉬低熱導率的原因在于較低的聲子群速度以及較大的Grüneisen常數,進而導致其聲子平均自由程僅為14.6 nm.其次,在單層石墨烯以及單層氮化硼中,面外ZA聲子模對熱導率貢獻占比均超過50%,但是在單層硫化鉬中面內聲子模式對熱導率的貢獻超過了面外的聲子模式[130].最后,與石墨烯以及氮化硼所不同,迄今為止實驗上測得單層/多層硫化鉬的面內熱導率均比硫化鉬塊材面內熱導率(85—110 W/(m·K),室溫)要低.該現象與理論上的預測不一致.顧驍坤等[131]預測單層硫化鉬的室溫面內熱導率能達到138 W/(m·K),其中原因可能是這些實驗中硫化鉬的質量均未達到較好的情況,或者背后隱藏著更深層次的原因有待進一步研究.

除了面內熱導率以外,硫化鉬的面間熱導率也是值得研究的問題之一,但是該方向的研究相對較少.最初Muratore等[138]和Cahill等[139]測量了塊材硫化鉬的室溫面間熱導率,僅為2—3 W/(m·K).但是,隨后科羅拉多博爾德分校楊榮貴課題組[75]在實驗上得到了一個數值更高的結果(約4.75 W/(m·K)),并且該結果與理論預測更加接近.上述實驗結果之間的差異在后續Sood等[74]的實驗中得到解釋.他們通過TDTR方法測量了不同厚度硫化鉬的室溫面間熱導率,結果顯示厚度為240 nm和20 nm的樣品室溫面間熱導率分別為2.0±0.3 W/(m·K),0.9±0.2 W/(m·K).通過與上述實驗數據的對比,發現隨著厚度增大,硫化鉬的面間熱導率呈增大的趨勢,當厚度達到1μm左右面間熱導率數值逐漸趨近于飽和閾值(約5 W/(m·K)).理論計算結果顯示硫化鉬面間聲子的平均自由程遠超之前的估計數值(1.5—4 nm),超過80%的熱量輸運是平均自由程為10—500 nm的聲子所貢獻的.

隨著二維材料的制備技術不斷發展,越來越多的多層過渡金屬硫化物被發現,因此它們的熱傳導性也在逐漸被研究.表4中列舉了不同文獻中除硫化鉬外其他過渡金屬硫化物的懸空面內熱導率實驗測量值.從表中數據看出,雖然這些材料的晶體結構很類似,但是其熱傳導性質卻存在明顯差異.

表4 除硫化鉬外,其他單層/多層過渡金屬硫化物的懸空熱導率實驗測量細節表Table 4.Experimental detail of thermal conductivity of single/few-layer transition metal sulfide(expect MoS2)in different literature.

3.1.4 黑磷、黑砷

同樣因帶隙可控、開關比較高等優點,黑磷(BP)是最早被研究的下一代微電子器件材料之一[140?142].但是最初研究人員對黑磷的熱傳導性質產生濃厚興趣,主要是因為其面內各向異性的“長城”狀結構[48],可能會導致熱導率的各向異性[143],如圖7(b)所示.值得注意的是,黑磷極易氧化,因此在有關黑磷的實驗中對于樣品在空氣中的暴露時間需要嚴格控制.

2015年中國科學院閆清波課題組[144]通過理論研究預測單層黑磷沿ZZ方向與AC方向的室溫面內熱導率比值能達到2.2(30.15 W/(m·K),ZZ方向;13.65 W/(m·K),AC方向),并且由于其“長城”狀結構導致面外聲子模式對熱導率的貢獻極低(約5%).很快,普渡大學Xianfan Xu課題組[58]在實驗上測量了室溫下不同厚度多層黑磷的懸空面內熱導率,在厚度最小(~10 nm)的樣品中ZZ方向熱導率為20 W/(m·K),而AC方向的熱導率僅為~10 W/(m·K),從而證實了上述理論預測.作為磷元素的同主族元素——砷,黑砷(BAs)的晶體結構與黑磷類似,因此其同樣具有明顯的面內熱導率各向異性效應.2018年伯克利大學吳軍橋課題組[145]首次在實驗上測量了厚度為124 nm的黑砷沿ZZ方向與AC方向的懸空面內熱導率(5 W/(m·K),ZZ方向;3 W/(m·K),AC方向,350 K).

后續實驗中,科研人員通過拉曼法、熱橋法等方法測量了不同厚度的多層黑磷的面內熱導率,均發現了面內熱導率的各向異性[48,49,73,77,146,147],具體內容見3.2.2及3.2.3節.在這些實驗中多層黑磷的厚度均在10 nm以上,這正是由于黑磷的化學性質過于活潑,在熱傳導實驗中單層黑磷的制備極其困難,因此關于單層或少層黑磷的熱傳導性質還有待進一步深入研究.

3.1.5碲烯

塊體碲(Te)是一種新型優質的熱電材料[148].同時其二維結構碲烯可以作為一種進一步提高其熱電性能的有效手段[149].在塊材中,碲原子通過共價鍵與一個鄰近原子相結合,并呈螺旋狀延伸,相鄰的螺旋鏈之間則通過范德瓦爾斯力結合[150],如圖7(c)所示,因此塊材碲屬于準一維的鏈狀結構.但是理論預測單層碲烯的結構與塊體碲不同,共有三種可能的晶體結構(a-Te、b-Te、g-Te)[151].Gao等[152,153]通過第一性原理計算研究了不同結構的單層碲烯的熱傳導及熱電性能,發現它們的熱導率均較低,并且熱電性質優異.但是迄今為止在實驗上只合成出b型碲烯,并且合成條件比較苛刻,因此暫未有關單層碲烯物理性質的實驗研究[154,155].

隨后2017年普渡大學Peide D.Ye課題組開發出一種液相合成方法[156],可以大量制備與塊材結構相同的多層碲烯.在進一步研究中,該課題組及其合作者通過拉曼法測量了厚度為35 nm碲烯的鏈內方向的室溫懸空熱導率(約1.5 W/(m·K)),與塊材(約3 W/(m·K),300 K)相比而言有一定程度的降低,他們認為其主要原因是多層碲烯的表面對聲子會產生一定的散射[157].由于該類碲烯的結構與塊材相同,因此其面內熱導率沿鏈內方向和鏈間方向會存在一定的差異,關于該類碲烯面內熱導率各向異性介紹,具體內容見3.2.3節.

3.1.6 硅烯

石墨烯被發現以后,作為碳的同族元素,硅烯自然而然被關注到.但是直到2012年硅烯才被合成出來,且生長條件極其苛刻[158,159].因此對于硅烯的熱傳導性質迄今為止均是圍繞理論研究而進行的,實驗研究暫無進展.

從結構而言,硅烯與石墨烯很相似,均為蜂窩狀結構.但是又有所不同,石墨烯的原子層平面比較平整,但是硅烯的原子層平面存在一定程度的褶皺,因此理論預測硅烯的熱導率較石墨烯至少低兩個數量級,并且面外ZA聲子模對熱導率的貢獻會比較低(約10%)[160,161].除了本征熱導率外,理論上還研究了利用應力[162]、電場[163]、缺陷[164]、同位素[165]等方法調控硅烯的熱導率,為未來硅烯的實驗研究提供指導.

3.1.7 其他二維材料

隨著納米材料制備技術和計算模擬技術的不斷發展,二維材料家族越來越龐大,不僅可以在實驗上合成某種新型二維材料,還可以通過理論模擬預測一些未知的二維材料.因此除了上述幾種材料以外,還有許多其他二維材料的熱傳導性質同樣已被研究.實驗方面,科研人員利用不同方法測量了多層碲化鉍[166]、多層硒化銦[167]、多層硫化錫[168]、碲化鋯納米帶[38]、多層氧化硒鉍[169]等二維材料的面內熱導率.理論方面也已經對硼烯[170]、單層氮化鎵[171]、單層氮化碳[172]、單層氮碳化硼[173]等二維材料的熱導率及相關性質進行了一定的預測研究.

3.2 尺寸效應及各向異性

由傅里葉定律可知,在塊體材料中熱導率與材料的尺寸無關.這主要是因為塊體材料的幾何尺寸遠大于聲子的平均自由程,此時聲子的輸運過程屬于擴散運動.但是在二維材料中,材料的幾何尺寸可以接近甚至小于聲子的平均自由程,使得聲子會從擴散輸運變為(準)彈道輸運,并且材料的表面或者邊界對聲子的散射效果會越發明顯,因而材料的熱導率會隨材料的幾何尺寸的改變而變化,出現長度效應、寬度效應以及厚度效應.

與尺寸效應不同,結構各向異性導致材料熱導率的各向異性是比較常見一種現象.例如在石墨、氮化硼、硫化鉬等塊體材料中,面內與面間的結合力性質不同,致使面內熱導率與面間熱導率的差別非常大,能達到兩個數量級左右.與此同時,某些二維材料(黑磷、碲烯等)不僅面內與面間的結構不同,其面內沿不同方向的結構同樣存在較大差異,因此這類二維材料為熱導率各向異性的研究提供了新的平臺.

3.2.1 長度效應和寬度效應

有關二維材料熱導率長度效應的理論研究,最早的研究對象是二維晶格Fermi-Pasta-Ulam lattice(FPU)體系.在該體系中發現材料熱導率與長度呈現對數發散的關系(k-logL)[11].石墨烯超高熱導率的發現提供了一個研究二維材料熱導率長度效應的理想對象.Nika等[101]認為隨著石墨烯的長度增大越來越多的低頻聲子被激發并參與熱傳導,因此當長度小于10μm時,石墨烯室溫熱導率隨長度變大而增加的趨勢將會非常明顯.通過進一步的研究,他們發現石墨烯熱導率的長度效應不僅僅取決于納米帶的長度,還與寬度以及邊界的粗糙度有關[174].在有限寬度以及邊界粗糙度較小的情況下,石墨烯納米帶熱導率與長度之間呈現一種非單調——先增大后減小的關系(取決于邊界粗糙度),并且室溫下長度效應范圍擴大至100μm.但是,Munoz等[105]通過彈道輸運研究提出石墨烯室溫熱導率的長度效應只有長度小于3μm才足夠明顯,這主要是基于他們認為室溫下石墨烯中聲子的平均自由程僅為0.6—1μm.可以看出聲子平均自由程大小是決定石墨烯長度效應范圍的關鍵因素.Knezevic等[104]通過蒙特卡羅模擬發現室溫下石墨烯中聲子的平均自由程遠超上述估計,其中約20%聲子的平均自由程大于100μm,約10%聲子的平均自由程超過200μm,如圖8(a)所示.

關于石墨烯熱導率與長度之間具體的數值關系,理論研究結果顯示室溫下長度為10—60 nm的石墨烯熱導率與長度呈指數關系(k-L0.4)[181],與單壁碳納米管熱導率的長度效應類似.但是隨著長度進一步增大(1—100μm),其熱導率隨長度變長呈對數增長(k-logL),并當長度超過100μm熱導率將逐漸趨近于某一飽和閾值[175],如圖8(b)所示.

在石墨烯熱導率寬度效應方面,聲子的邊界散射是核心因素.在塊材石墨中邊界散射對聲子整體的輸運影響可以忽略,但是在石墨烯中其寬度能夠與聲子波長相近,因此邊界散射的影響會非常明顯.理論研究的結果比較統一,隨著寬度變大,聲子的邊界散射逐漸減弱,其熱導率隨之增大,但是寬度效應的范圍問題還未有具體的研究結果.

圖8(a)室溫下單層懸空石墨烯中聲子平均自由程[104];(b),(c)理論及實驗上單層懸空石墨烯室溫熱導率隨長度變化[17,102,175,176];(d)實驗上不同寬度的單層石墨烯懸空熱導率隨溫度變化[17,98,177?180]Fig.8.Single-layer suspended graphene(a)the mean free path at room temperature[104];(b),(c)length-dependent thermal conductivity in theory and experiment respectively[17,102,175,176];(d)width-dependent thermal conductivity in experiment[17,98,177?180].

實驗方面,2014年徐象繁等[17]使用懸空熱橋法測量了不同長度(300 nm—9μm)的懸空單層CVD石墨烯的面內熱導率,在接觸熱阻占比不同的情況下均發現石墨烯室溫本征面內熱導率與長度之間呈對數發散的關系,且未觀測到飽和閾值,如圖8(c)所示.同時,對寬度效應也進行了實驗證實.在相同的長度(2.5μm)情況下,石墨烯寬度變小(4μm→1.5μm)時其室溫熱導率數值也會有所降低(約1186 W/(m·K)→約1054 W/(m·K)).同年,Bae等[111]對石墨烯在襯底上的室溫熱導率的長度效應也進行了研究,相較懸空石墨烯而言其達到飽和閾值的長度(約5μm)要低很多,他們認為這主要是因為石墨烯在襯底上導致聲子的平均自由程降低(90 nm,300 K),并且也觀測到了熱導率隨寬度減小而降低的現象.此后,Takamatsu等[177]通過實驗研究在單層懸空石墨烯中觀察到了熱導率的寬度效應與溫度的關系,室溫下熱導率的寬度效應很明顯,寬度為2μm和1μm的樣品熱導率分別為2295 W/(m·K)、1739 W/(m·K).但是隨著溫度進一步升高寬度效應將逐漸消失,他們認為這主要是因為溫度越高,聲子的U型散射越嚴重,導致聲子的平均自由程降低,邊界散射的影響逐漸減弱,如圖8(d)所示.

此外,最近北卡羅萊納州立大學Cao linyou課題組[18]在單層、雙層以及三層硫化鉬、單層硒化鎢和單層硫化鎢中同樣觀察到了懸空樣品室溫熱導率的尺寸效應.該實驗所采用的測量方法為拉曼法,樣品懸空部分形狀為圓形.通過改變懸空部分的半徑尺寸(1.8—6.0μm),發現樣品的室溫熱導率與半徑(D)之間同樣呈現對數發散關系(k-logD),與理論預測一致[182,183].他們認為熱導率隨半徑增大是由于更多的低頻聲子被激發并參與熱輸運過程.通過與相關實驗文獻對比,發現使用拉曼法測量單層/多層硫化鉬時熱導率與懸空部分尺寸之間的確存在一定的關系,如圖9所示.

關于氮化硼、黑磷等二維材料熱導率的長度效應或寬度效應均未有實驗報道,但是在理論方面擁有一些研究.例如,Mukherjee等[184]利用第一性原理計算發現在單層氮化硼中面內熱導率的長度效應與石墨烯很相似,當長度處于1—100μm范圍內時室溫熱導率與長度之間呈對數關系.李保文課題組[185]采用求解玻爾茲曼方程的方法預測在單層黑磷中ZZ方向室溫熱導率的長度效應能達到100μm,但是AC方向室溫熱導率的長度效應僅在1μm以下才足夠明顯.

圖9使用拉曼法測量單層/多層硫化鉬時熱導率與懸空部分半徑之間的關系[18,60,127,128]Fig.9.Thermal conductivity of single/multi-layer MoS2 versus suspended radius using the Raman method.[18,60,127,128].

最新研究結果顯示,二維材料特別是石墨烯和氮化硼中的高熱導率及反常熱導率可能與聲子流體動力學及由此產生的第二聲有一定的關聯.傳統的聲波(或叫做第一聲)是指壓力在空間的周期變化.第二聲的概念源于氦Ⅱ,在低溫下聲子可傳播幾毫米甚至厘米的距離而不受散射(彈道輸運);在高溫下由于三聲子的U型散射而進行擴散輸運.聲子流體動力學行為通常出現在彈道輸運和擴散輸運之間狹小的溫度窗口[186,187].強烈的U型散射會抑制聲子流體動力學行為的發生,使得初期觀測到的第二聲行為都是在極低溫環境下,如3He(T=0.42 K–0.58 K)[188],Bi(T=1.2—4 K)[189],NaF(T=11—14.5 K)[190,191].有理論預測,二維材料存在的面外聲子模式可引起增強的正常散射(Nscattering),同時隨著厚度降低導致U型散射的減弱,這使得石墨烯等二維材料中的聲子流體動力學行為溫度窗口會大大增加[192?194].雖然未有實驗可以驗證理論的合理性,但是最近的兩個石墨熱導率的工作顯示石墨塊體/薄片中的第二聲可在高達T=100 K的溫度下存在[194,195].同時由于第二聲的貢獻, 石墨薄片的熱導率最高可達4300 W/(m·K).Wang等[90]最近的實驗也顯示石墨薄片的熱導率隨著厚度的降低而增加,并在800 nm厚的石墨薄片中觀測到3200 W/(m·K)的熱導率;雖然該文作者將其歸納為樣品質量的變化,但是其高熱導率及厚度效應也可能與第二聲有關.

3.2.2 厚度效應

從三維塊體到(準)二維平面,材料的熱導率會發生非常大的變化,因此研究二維材料熱導率的厚度效應對解釋上述變化是至關重要的.同時,該項課題涉及到一個非常有意思的科學問題:幾層二維材料可視為三維塊體?

實驗上所觀察到的二維材料懸空熱導率的厚度效應可以分為兩類:(1)以石墨烯、氮化硼為代表的二維材料,隨著厚度的增大,其熱導率逐漸下降,直至與塊材相近;(2)以黑磷為代表的其他二維材料,由于邊界散射, 其熱導率隨厚度增加而增大.

2010年Ghosh等[64]測量了不同層數(1—10層)的懸空石墨烯室溫熱導率,發現隨著層數增加熱導率數值逐漸下降,當層數達到4層時其數值已基本接近塊材熱導率,如圖10(a)所示.他們認為上述現象的出現是由于層間耦合導致低頻聲子散射變強,引起熱導率降低.除了懸空熱導率的厚度效應外,襯底上的石墨烯熱導率同樣具有厚度效應,但是變化趨勢與懸空石墨烯有所不同——隨層數增加,熱導率呈現變大或不變的趨勢[103,110,196,197].主要原因是非懸空樣品中ZA聲子得到了極大抑制,這點我們在前文中已做過相應討論.

Lindsay等[119]通過模擬計算預測單層氮化硼的熱導率厚度效應與石墨烯很類似.隨后同濟大學徐象繁課題組[41,44]測量了兩層和四層氮化硼的懸空熱導率,通過比較可以看出熱導率隨厚度增大有逐漸減小的趨勢.當厚度增加到四層時,熱導率值已經接近文獻報道塊體熱導率,同時四層樣品低溫熱導率隨著溫度呈現T2.5行為,表明四層氮化硼熱導行為可能已經接近塊體,如圖10(b)所示.最近李璐華等[56]測量了不同厚度(1—3層)的氮化硼的懸空熱導率,同樣觀察到隨著厚度增大,熱導率逐漸下降,但是與石墨烯相比氮化硼厚度效應不是特別明顯,如圖10(c)所示.通過分子動力學模擬,他們發現隨著層數增大,氮化硼的Grüneisen常數以及ZA聲子模(對熱導率貢獻很大)的頻率會變大,從而導致了聲子的散射會加強,熱導率降低.

然而,單層石墨烯和單層氮化硼熱導率的極限值是多少仍未有定論,這個問題不管是實驗還是理論方面都存在爭議.同時,塊體石墨和塊體氮化硼熱導率值也未有定論.因此,四層石墨烯和四層氮化硼的熱導率是否和塊體本征熱導率一致仍有所質疑,需大量實驗工作驗證.

圖10(a)石墨烯(懸空/襯底)面內熱導率的厚度效應[64,103,110,196,197];(b)四層氮化硼懸空熱導率與溫度之間的關系[44];(c)氮化硼(懸空)面內熱導率的厚度效應[41,44,56,120,198];(d)硫化鉬(懸空)面內熱導率的厚度效應[18]Fig.10.(a)Thickness-dependent in-plane thermal conductivity of graphene(suspended and supported)[64,103,110,196,197];(b)thermal conductivity of four-layers h-BN(suspended)versus temperature[44];(c)thickness-dependent in-plane thermal conductivity of h-BN(suspended)[41,44,56,120,198];(d)thickness-dependent in-plane thermal conductivity of MoS2(suspended)[18].

黑磷熱導率的厚度效應在實驗上的結果相對比較統一,其熱導率隨厚度增大而增大,如圖11所示.但是在這些實驗中黑磷的厚度基本都是10 nm以上(層數至少在10層以上),因此厚度為10 nm以下的黑磷熱導率隨厚度變化的趨勢有待進一步研究,可能存在與現有結果不一樣的情況.除了黑磷以外,在碲烯[199]、多層硒化銦[167]、多層硫化錫[168]、多層碲化鎢[136]、多層碲化鉍[43]、多層氧化硒鉍[169]、碲化鋯納米帶[38]等二維材料中均觀察到了類似的熱導率隨厚度變化的關系.

圖11室溫下黑磷面內熱導率的厚度效應及各向異性[48,49,73,77,146,147,168,200]Fig.11.Thickness-dependent and anisotropic in-plane thermal conductivity of the BP[48,49,73,77,146,147,168,200].

理論上預測硫化鉬的熱導率與其厚度(層數)之間的關系為隨厚度增大室溫熱導率會呈現降低的趨勢,并在四層左右接近于塊材的室溫熱導率[131].但是實驗上觀測懸空硫化鉬熱導率的厚度效應存在一定的爭議:有些實驗沒有觀測到明顯的厚度效應[54],還有一些觀測到的厚度效應與懸空石墨烯相反—隨厚度增大熱導率也逐漸增大[128].稍顯詫異的是在某些實驗中發現懸空硫化鉬熱導率與層數之間呈現一種非單調的變化關系(先減小后增大)[70].上述結論均是在不同文獻的實驗數據之間進行比較而得出的,因此可靠性還有待進一步確認. 但是2018年王信偉課題組[65]在實驗上觀測到了襯底上的硫化鉬熱導率與厚度(2.4 nm—37.8 nm)之間的非單調變化,隨著厚度增大,熱導率先減小后變大.他們認為在較薄的硫化鉬中聲速隨著厚度增大而減小,并且材料的對稱性被破壞,因此會出現熱導率降低的趨勢.但是在較厚的硫化鉬中,聲子的表面散射的影響會隨厚度增大而減弱,進而出現熱導率增大的現象.最近,Yu等[18]在實驗中觀測到懸空硫化鉬的室溫熱導率隨層數增加(一層至四層)而減小,如圖10(d)所示.但是其熱導率數值是從約60.3 W/(m·K)減小至約36.9 W/(m·K),最終并未與硫化鉬塊材室溫熱導率相接近,因此關于懸空硫化鉬的熱導率隨層數的變化關系還有待實驗上進一步的驗證.

3.2.3 各向異性

在石墨烯、氮化硼、硫化鉬等二維材料中面內不同方向的結構差別較小.雖然在理論計算中熱導率能夠體現出微小差別,但是在實驗上還未觀測到熱導率各向異性的存在.比較特殊的是黑磷、黑砷以及碲烯,它們的面內結構各向異性非常明顯,因而其熱導率各向異性的現象會比較突出,能夠在實驗上觀察到.

利用拉曼法,Xu Xianfan課題組[58]首次測量了不同厚度以及不同方向的黑磷室溫面內熱導率,結果顯示其熱導率數值具有明顯的各向異性,同時隨著厚度變化,ZZ方向的熱導率與AC方向熱導率的比值也會有所變化——當厚度大于15 nm時,上述比值能達到2左右;但是在最薄(厚度9.5 nm)的樣品中,上述比值變成了3左右.他們認為黑磷面內熱導率的各向異性是由結構的各向異性導致聲子色散關系各向異性而引起的.同年,Lee等[48]發現黑磷面內熱導率的各向異性除了與厚度有關外,還與溫度有關.當溫度低于100 K時,ZZ方向與AC方向熱導率數值差別很小,但是隨著溫度升高,其各向異性愈發明顯.圖11中列舉了不同文獻中關于黑磷面內熱導率各向異性的實驗結果.在多層黑砷中,同樣存在熱導率的各向異性現象.吳軍橋等[145]發現室溫下黑砷ZZ方向的熱導率與AC方向的熱導率的比值接近1.8,與黑磷的情況類似,如圖12(a)所示.

近期,關于碲烯的面內熱導率各向異性在實驗上也被證實,Xu Xianfan課題組[199]使用拉曼法測量了碲烯面內不同方向的熱導率,結果顯示室溫下鏈內熱導率與鏈間熱導率的比值能夠達到1.3以上,呈現出明顯的各向異性特性.同時通過第一性原理計算,他們認為鏈內聲速大于鏈間聲速是導致碲烯熱導率各向異性的根本原因.

關于黑磷面內熱導率各向異性的起源,文獻中的觀點主要集中在兩個方面[48,73,77,146,147]:(1)聲子色散關系的各向異性;(2)聲子弛豫時間的各向異性.2018年趙云山等[49]在實驗中不僅測量了黑磷面內熱導率,還使用AFM測量了同一樣品的楊氏模量,如圖12(b)所示,結果顯示黑磷的面內熱導率的各向異性比值與楊氏模量各向異性比值非常接近,因此他們認為黑磷面內熱導率各向異性的真正起源應該是聲速的各向異性.

圖12(a)多層黑砷懸空面內熱導率的各向異性[145];(b)黑磷沿ZZ方向、AC方向懸空面內熱導率以及楊氏模量數值(300 K)[49]Fig.12.(a)Anisotropic in-plane thermal conductivity of suspended few-layer BAs[145];(b)the Young modulus and in-plane thermal conductivity of suspended BP along AC and ZZ direction respectively at 300 K[49].

3.3 二維材料熱導率調控

3.3.1 同位素效應

廈門大學蔡偉偉課題組通過13C摻雜調控單層石墨烯的懸空熱導率,結果顯示隨著13C摻雜比例的提高,石墨烯熱導率呈現先下降后上升的趨勢[201].開始階段隨著同位素摻雜比例提高,聲子受到的散射會愈發嚴重,因此熱導率存在降低的情況.例如與摻雜比例為0.01%的樣品相比,摻雜比例為50%的樣品室溫熱導率降低了50%.當摻雜比例達到一定程度后,摻雜原子13C反而主導了熱輸運過程,此后提高13C摻雜比例,其實是降低了“雜質”(12C)比例,因此高摻雜樣品熱導率反而有所上升.該實驗現象的發現引起了一定的關注,相關理論研究相繼發表[202?204].Fugallo等[202]通過求解玻爾茲曼輸運方程的方法,改變石墨烯中13C的摻雜比例所得到的熱導率變化趨勢與實驗測量相同,如圖13(a)所示.

3.3.2 晶粒/晶界效應

材料內部晶粒的大小以及晶界的夾角等均會影響聲子的弛豫時間,導致材料的熱導率降低.Lee等[205]通過控制合成條件進而控制石墨烯中晶粒的尺寸,并發現石墨烯的懸空熱導率隨晶粒尺寸的減小而降低,如圖13(b)所示.他們認為石墨烯中熱導率主要由低頻長波聲子貢獻,晶粒尺寸愈小,聲子的散射愈嚴重.此外Malekpour等[206]在石墨烯壓層材料中觀察到材料熱導率隨石墨烯片尺寸變大而呈增大的趨勢.由于石墨烯片的尺寸較小(微米級別,與聲子平均自由程相似),可以將其理解成晶粒,因此同樣可以利用上述理論解釋該現象.

此外,可以用鏡面反射系數P描述在晶界處的聲子散射行為.鏡面反射系數與界面夾角(q)之間的關系可以表述為P-exp(–C1×sin2q),其中C1為經驗常數.可以看出小角度情況下隨著晶界夾角增大,鏡面反射系數會降低,從而導致聲子散射加強.Lee等[207]在單晶/雙晶/多晶石墨烯中證實了上述現象,雙晶石墨烯的懸空熱導率隨著晶界夾角增大呈現下降趨勢,尤其是小角度(<4°)時,隨著晶界夾角的增大,熱導率下降的非常迅速,如圖13(c)所示.同時當夾角較大時,熱導率數值將出現飽和,不再繼續減小,用上述理論可以很貼切的解釋該實驗現象.

3.3.3 雜質/缺陷效應

與同位素效應相似,在二維材料中引入雜質或缺陷,同樣能夠起到調控熱導率的作用.通過在石墨烯上沉積金原子并改變金原子在石墨烯上的覆蓋率,李保文課題組[109]發現隨著金原子覆蓋率的增大,石墨烯熱導率呈先減小后增大的趨勢.他們認為金原子較重,能夠抑制石墨烯中的ZA聲子模,因此出現熱導率降低的現象.但是當金原子覆蓋率達到一定程度后,金原子本身就能形成一個傳熱網絡,導致后續熱導率呈增大趨勢.

圖13懸空石墨烯面內熱導率(a)同位素效應[202];(b)晶粒尺寸的影響[205];(c)晶界夾角的影響[207];(d)空位率的影響[208]Fig.13.In-plane thermal conductivity of suspended graphene:(a)Isotope effect[202];(b)influence of grain size[205];(c)influence of misorientation angle between grains[207];(d)influence of vacancy ratio[208].

其次理論上預測石墨烯的熱導率會隨其晶格結構中的空位率的增大而降低,但是在石墨烯制備過程很難控制空位形成的比例及其均勻性[209].Malekpour等[208]以及Lee等[210]利用電子束轟擊石墨烯表面形成規則且均勻的孔洞代替晶格中的空位,結果顯示隨著孔洞面積占比增大,其熱導率呈下降趨勢,與理論預測一致,如圖13(d)所示.隨后Oh等[211]通過進一步研究發現除了孔洞面積占比外,相鄰孔洞之間的距離也是影響石墨烯熱導率的一個關鍵因素.聲子散射會隨孔洞間距的減小而增強,石墨烯熱導率隨之減小.此外,Yarali等[212]在制備單層硒化鉬的過程中進行鎢原子替代硒原子并產生一定的空位,測量結果顯示經過處理的樣品熱導率比未經處理的樣品熱導率偏低.

與此同時,通過摻雜引入雜質原子進而調控熱導率也是一種行之有效的方法[213,214].利用氧等離子體對石墨烯[215]及多層硫化鉬[45,216]進行摻雜在實驗上已經得以實現.同濟大學徐象繁課題組[45]采用上述方法并結合電子束自加熱法研究了多層硫化鉬室溫懸空熱導率與氧離子的摻雜濃度之間的關系,實現了從多晶到非晶的熱導率連續調控(約30 W/(m·K)→約2 W/(m·K)). 結合分子動力學模擬,他們發現當摻雜濃度比較低的時候,聲子-缺陷散射導致聲子透射系數下降并引起熱導率的快速且大幅度的減小;隨著摻雜濃度繼續提高,熱導率的下降趨勢則相對平緩,最終能夠接近非晶材料熱導率的極限值,如圖14所示.通過高分辨率透射電子顯微鏡也證實晶體結構從多晶到非晶的轉變.

3.3.4 熱整流效應

與電流二極管類似,熱整流效應是指熱流沿某一方向較相反方向更容易通過的現象.熱整流效應是實現熱二極管、熱三極管、熱邏輯門以及聲子計算機的基礎.1936年Starr等[217]首次在銅以及氧化亞銅界面處發現熱二極管現象[217].隨之一系列熱二極管的理論與實驗相繼出現[218].在塊體材料中熱二極管的設計理論主要包括:(1)利用界面處電流二極管現象產生熱二極管效應;(2)利用界面處兩種材料的接觸應力或接觸面粗糙度隨溫度改變產生熱二極管效應;(3)利用界面處的熱勢壘產生熱二極管效應;(4)利用界面兩側材料的熱導率與溫度依賴關系不同產生熱二極管現象.

圖14 懸空硫化鉬面內熱導率[45]:缺陷濃度的影響Fig.14.In-plane thermal conductivity of suspended MoS2 [45]:influence of defect concentration.

隨著集成電路的微型化,微納尺度的熱二極管在散熱方面的應用越發受到重視.微納尺度熱二極管的設計理論與塊材有相似之處,也存在一定區別.非對稱結構(形貌、應力、缺陷等)是實現微納尺度熱二極管的主要方法,其物理機制存在以下兩種解釋:(1)兩種結構的熱導率隨溫度變化的趨勢不同.例如A結構的熱導率隨溫度升高而增大,但是B結構的熱導率隨溫度升高而降低,改變熱流方向它們整體的平均熱導率會發生變化,即能夠實現熱二極管效應,如圖15(a)所示;(2)兩種結構的聲子譜不一致,熱流方向不同時聲子譜之間的重疊情況會發生變化,聲子譜重疊程度越高,熱流能夠更順利的通過[219],如圖15(b)所示.實驗上低維材料的熱整流效應最開始是通過在碳納米管以及氮化硼納米管上非均勻沉積重金屬原子實現的[220].隨后在形貌非對稱的氧化釩納米線[221]、Y-型碳納米管[40,222]中以及聚酰亞胺納米線/硅納米線異質結構[223]中均觀測到了熱整流效應.

由于二維材料非對稱結構的制備技術存在一定難度,因此最初關于二維材料的熱整流效應研究主要集中在理論方面.2009年楊諾等[225]利用分子動力學模擬在非對稱單層石墨烯結構(梯形以及雙矩形)中發現了熱整流現象.隨后大量關于非對稱二維材料結構(三角形、Y-型、缺陷等)的熱整流效應的理論工作接踵而出,為后續實驗觀測提供一定指導[219,226?230].

直到2017年Takamatsu課題組[224]才在實驗上實現了懸空單層石墨烯中的熱整流現象.在該實驗中,石墨烯一側保持完整結構,但是在另一側被掏孔、沉積重原子或剪裁,如圖15(c)所示.在一側被掏孔的石墨烯樣品中,當熱流從結構完整一側往結構被破壞一側傳導時所受阻礙較大,因而觀測到了約27%的平均整流率,如圖15(d)所示.他們認為完整結構部分和被掏孔部分石墨烯熱導率的不一致是導致熱整流效應出現的主要原因.

4 二維材料界面熱阻研究進展

圖15微納尺度熱二極管設計原理(a)熱導率隨溫度變化趨勢不同;(b)聲子透射率不對稱[219];非對稱結構懸空石墨烯[224](c)SEM圖;(d)熱二極管實驗結果Fig.15.Design principle of thermal diode in micro/nano-scale:(a)Different tendency between thermal conductivity and temperature;(b)asymmetric phonon transmission ratio[219];asymmetric structure of suspended graphene[224](c)SEM image;(b)the experiment result of thermal diode.

在熱傳導領域,不僅材料本身的熱導率是一個重要的研究方向,不同材料間的界面熱阻也是非常關鍵的.尤其在復雜的電子器件中,決定器件散熱能力的往往不是各材料的本征熱導率數值,而是各種界面之間的熱阻大小[4,231?233]. 如對于h-BN/SiO2界面,其界面熱阻測量值為1.6×10–8m2·K/W,取SiO2熱導率為1.1 W/(m·K),則其Kapitza長度為17.6 nm,即BN/SiO2界面熱阻值與17.6 nm SiO2的熱阻值相同[234].因此在未來二維材料的應用過程中,二維材料與其他材料的界面熱阻問題需要引起足夠的重視.

1941年Kapitza在銅與液氦的界面上觀察到溫度場的突變,從而提出了界面熱阻(Kapitza熱阻)的概念.界面熱阻Rint=DT/J,其中DT為界面處溫度場的突變值,J為單位時間內通過單位面積的熱流大小.關于界面熱阻的大小,主要有兩種理論進行估算——聲子失配理論(acoustic mismatch model, AMM)[251]與擴散失配理論(diffusive mismatch model,DMM)[252].AMM模型假設界面是理想光滑的,在界面處聲子發生完全鏡面反射或透射,因此只有在低溫環境中或對于低頻聲子,即當聲子波長遠大于界面粗糙尺寸,該模型是成立的.DMM模型則假設聲子在界面處發生散射時失去了除頻率外的所有信息,因而聲子透射率與界面兩側材料的聲子態密度的匹配程度密切相關.很顯然,上述兩種模型對于界面處聲子行為的假設過于簡單.大量實驗結果也證實,上述兩種理論的計算值與實驗值普遍存在巨大差別,因此對于界面熱阻的機理還有待進一步研究[253].

作為襯底,介電材料和金屬材料是被研究較多的[254].2009年Dames等[237]利用3w法測量了機械剝離石墨烯與氧化硅襯底之間的界面熱阻.他們發現隨溫度升高界面熱阻數值逐漸降低,室溫下界面熱阻Rint=5.6—12×10–9m2·K/W,同時發現界面熱阻與石墨烯厚度(1.2—3 nm)之間不存在明顯的聯系.隨后Villaroman等[239]研究了CVD石墨烯與不同金屬(Au,Ti,Al)之間的界面熱阻,其數值為(2—5)×10–8m2·K/W.隨著二維材料家族的不斷發展,同濟大學徐象繁課題組[234]測量了多層氮化硼與氧化硅襯底之間的界面熱阻((1.3—3.5)×10–8m2·K/W),并發現界面熱阻數值與氮化硼厚度之間呈一定正相關,如圖16(a)所示.他們認為這是由于使用機械剝離的方法制備較厚的氮化硼會在界面處引入比較多的空位以及空隙所造成的.在硫化鉬與晶體硅襯底的界面熱阻實驗中,王信偉課題組[244]觀察到界面熱阻數值隨硫化鉬厚度增大而減小的現象,同樣與硫化鉬與襯底的接觸情況有關.

圖16(a)氮化硼厚度對金屬/氮化硼/氧化硅界面熱阻的影響[234];(b)利用3w法測量不同方法制備的氮化硼對硒化鎢器件的界面熱阻的影響[250];(c)在界面處引入化學鍵對金屬/單層石墨烯/氧化硅界面熱導的影響[256];(d)在界面處加電壓對氧化硅/多層石墨烯/氧化硅界面熱阻的影響[257]Fig.16.(a)Thickness-depend interfacial thermal resistance of metal/h-BN/SiO2[234];(b)interfacial thermal resistance of WSe2 device with h-BN prepared by different method[250];(c)improving interfacial thermal resistance of Al/single-layer graphene/SiO2 by introducing chemical bond[256];(d)the influence of voltage at interface to interfacial thermal resistance of SiO2/graphene/SiO2[257].

表5中列舉了部分常見二維材料與襯底之間界面熱導Gint=1/Rint的實驗測量值.從表5中數據可以看出,襯底材料對界面熱傳導的影響非常大.對于同種二維材料與不同襯底之間的界面熱導數值變化能達到1—2個數量級的變化,因此選擇合適的襯底材料對于提高二維材料的界面熱導是至關重要的.在分析界面熱導時,聲子透射率是一個關鍵的因素.界面處聲子透射率越大,往往界面熱導越高.石墨烯/碳化硅之間的界面熱導(約28 MW/(m2·K),室溫)相較石墨烯與氮化硼之間的界面熱導(約186 MW/(m2·K),室溫)要低很多,其核心原因就是石墨烯與氮化硅之間的聲子透射率非常低[255].其次,兩種材料的德拜溫度的匹配程度也可以作為分析依據.界面熱導會隨著兩種材料德拜溫度的差值增大而減小.金剛石的德拜溫度較石墨烯德拜溫度高出很多,導致石墨烯與金剛石之間的界面熱導相較其他介電襯底偏低[245].

除了聲子透射率以及德拜溫度匹配程度以外,即使是相同的界面材料,其界面熱阻可能依舊存在較大差別,這主要與界面處材料之間的結合情況有關.例如采用機械剝離方法制備的二維材料與襯底之間往往會存在一定空隙、缺陷、水蒸氣、有機物殘留等,從而使用CVD方法直接在襯底上生長二維材料將大大改善上述問題.例如同濟大學徐象繁課題組測量了硫化鉬/氧化硅之間的界面熱阻,在該實驗中多層硫化鉬是直接利用CVD方法生長在氧化硅襯底上的,其實驗結果(約4.76×10–8m2·K/W)較其他通過轉移所制備的樣品要低至少一個數量級[243].此外,他們在硒化鎢器件的界面熱導實驗中發現通過等離子增強CVD法所制備的單層氮化硼比普通CVD法所制備的單層氮化硼能夠使器件的界面熱導降低的更多一些(圖16(b)),其中原因就在于前者與襯底之間結合更加緊密[250].

在普通界面處兩種材料是通過范德瓦爾斯力結合在一起的,如果能夠在界面處引入相互作用更強的結合鍵(共價鍵等)將能夠在一定程度上提高界面熱導[256,258].Hopkins等[256]通過氧等離子轟擊在金屬/石墨烯界面引入C-O共價鍵,測量結果顯示相較未經處理的樣品,經過等離子處理的樣品的界面熱導提高了一倍,如圖16(c)所示.除此之外,實驗還發現經過退火處理能夠在金屬鈦/石墨烯的界面處引入Ti—C健,從而也可以提高其界面熱導[239].更進一步,Koh等[257]通過在石墨烯/氧化硅界面處加上一定電壓,增強界面耦合的強度,同樣可以起到提高界面熱輸運的作用, 如圖16(d)所示.

表 5常見二維材料的界面熱導實驗測量值Table 5.Experimental results of interfacial thermal conductance of two-dimensional materials.

一般而言,聲子是非金屬中熱能輸運的主要載流子,而電子則是金屬中的主要熱載流子.當熱流通過金屬和非金屬的界面處時,兩者界面處存在熱能的傳遞,如圖17插圖所示.其中Q表示要通過界面的熱流總量,藍色和紫色的圓球分別代表兩種材料中的聲子和電子,綠色(左)和黃綠色方塊(右)分別表示金屬和非金屬材料.考慮到所有可能存在的熱輸運通道,可以將其大致分為三類,即Q=Q1+Q2+Q3,其中,Q1表示界面處金屬中的電子和非金屬中的聲子直接耦合以實現熱能的傳遞,用藍色的箭頭表示[260];Q2表示金屬內部的電子和聲子首先耦合將能量傳給聲子,隨后在界面處實現聲子-聲子耦合來傳遞熱能,用紅色的箭頭表示;Q3表示金屬中的聲子和非金屬中的聲子耦合來傳遞熱能,用黑色的箭頭表示.通過這三種方式(主要是Q3),共同傳遞了界面處總量為Q的熱能.因此,如果在非金屬表面引入一薄導電層,則可以重新增加一個導熱通道Q4:即金屬中的電子首先傳導至非金屬表面導電層,然后再通過電-聲耦合將熱量傳導至非金屬.在此基礎之上利用氧離子轟擊非金屬表面,同濟大學徐象繁課題組[259]發現金-氧化鋁的界面熱阻會大幅度降低,如圖17所示.在排除接觸面粗糙度變化、產生化學鍵等因素的情況下,他們提出經氧離子處理的非金屬表面載流子濃度會隨處理時間增大而增大,進而會出現一種新的熱量傳遞機制—金屬一側的電子與非金屬表面的載流子產生耦合隨之載流子會與非金屬的聲子進行耦合并傳遞熱量.如果將該方法用于改善石墨烯與介電襯底之間的界面熱阻同樣是適用的.

圖17 通過氧離子束轟擊改善金屬與非金屬的界面熱阻[259]Fig.17.Improving interfacial thermal resistance of metal/nonmetal by O2-plasma[259].

通過上述分析可以看出,影響界面熱阻的因素比較多,通過某種單一措施想獲得超低的界面熱阻是比較困難的,因此在未來的研究中需要更多的考慮多重因素共同作用的效果.

5 二維材料在散熱方面的研究進展

散熱問題的處理始終伴隨著電子器件的發展,尤其是近年來集成電路元件逐漸向微型化發展,電子器件的集成度越來越高,運行時所產生的熱功率可高達1000 W/cm2[4,231?233].熱量的積聚會嚴重影響電子器件的運行效率以及壽命,因此散熱問題已經成為制約集成電路進一步發展的瓶頸.為了提高器件的散熱性能,散熱材料應該具備輕薄、高熱導率以及低界面熱阻等特性.傳統的電學器件散熱材料,例如鋁、銅等,雖然擁有較高的熱導率,但是往往體積很大、質量很重,使得器件整體看起來比較笨重.二維材料的發現,給科研工作者提供了一條新的解決思路.

在散熱方面的應用,石墨烯在眾多二維材料中最具代表性[23].其具有超高熱導率并可以將單層/多層石墨烯直接作為散熱材料[261].Balandin等[262]利用高度取向的熱解石墨(HOPG)進行機械剝離獲得多層石墨烯并將其轉移至氮化硅襯底上.當襯底上的AlGaN/GaN晶體管以約13 W/mm2的高功率運行時器件“熱點”溫度較無石墨烯的情況降低了20℃,說明石墨烯能夠快速的將“熱點”處的熱量擴散出去,預測器件的使用壽命至少能夠延長十倍.上海大學劉建影課題組[263]進一步將CVD單層及多層石墨烯轉移到硅襯底上,當襯底上的器件運行時同樣觀察到“熱點”的溫度有明顯的降低.同時單層石墨烯較多層石墨烯散熱效果更加理想一些.通過對比,Bae等[264]發現以石墨烯為基礎的散熱元件與以金材質為基礎的散熱元件相比,襯底上的溫度分布更加均勻.

雖然機械剝離石墨烯較CVD石墨烯質量普遍要好一些且熱導率更高,但是機械剝離方法不適用于大規模的工業制備和生產,因此提高CVD石墨烯的質量是非常有必要的.隨著近幾年CVD制備技術的不斷進步,CVD石墨烯的質量已經有了一定的提高.例如Lee等[265]成功在鍺襯底上生長出晶圓尺度且光滑無褶皺的單層單晶石墨烯.中國科學院謝曉明課題組[266]在CuNi合金襯底上實現快速生長英寸尺度的單晶石墨烯.

盡管單層/多層石墨烯已經證實可以直接作為電學器件的散熱材料,但是其散熱能力有限,面對高密度熱流其散熱效果會大打折扣,因而將大量石墨烯制成薄膜可以作為一種新的方案.在實際操作中制備石墨烯薄膜一般需要經過兩個步驟——原材料解離和制膜. 解離步驟常見方法包括超聲解離、球磨等,制膜流程的常見方法包括真空過濾、靜電紡絲、噴涂印刷、自組裝、旋涂等.實驗上石墨烯薄膜的熱導率基本維持在1000—1400 W/(m·K)[267?269],雖然該數值較商業熱解石墨片偏低,但是石墨烯薄膜在柔韌型以及尺寸控制方面的優勢很突出.石墨烯薄膜低熱導率主要原因是薄膜中晶粒小而多,還存在大量褶皺、錯位排列等導致聲子散射嚴重.為了解決這一問題,上海大學劉建影課題組[90]通過嚴格控制制膜過程中的溫度以及壓強大幅度提高了石墨烯薄膜的熱導率,厚度為0.8μm的薄膜熱導率能夠達到3200 W/(m·K),如圖18(a)所示.

石墨烯不僅可以直接作為散熱材料,將其與其他材料混合制成的復合材料能夠在一定程度上提高原有材料的散熱性能,例如將其與有機物混合可以作為熱界面材料(thermal interface materials,TIMs). 將單層/多層石墨烯與環氧樹脂混合, Shahil等[270]發現隨著摻雜比例提高混合物的熱導率逐漸變大,摻雜體積比為10%的樣品熱導率較環氧樹脂增加了2300%,達到約5.2 W/(m·K),如圖18(b)所示.同時他們在商業導熱油脂中做了同樣的摻雜實驗,發現摻雜比例僅為2%就能將室溫熱導率由原來的約5.8 W/(m·K)提高到約14 W/(m·K),并且力學性質在摻雜前后并未發生明顯變化.

圖18(a)經高溫退火的石墨烯薄膜的熱導率與厚度之間的關系[90];(b)石墨烯與環氧樹脂混合作為TIMs材料[270]Fig.18.(a)Thickness-depend thermal conductivity of graphene film with high-temperature annealing[90];(b)mixture of graphene and epoxy as TIMs [270].

石墨烯面內熱導率遠遠高于其面間熱導率,如果能夠使石墨烯在界面處縱向排列,利用其面內的高熱導率充當熱界面材料將會有比較好的效果.北京大學白樹林課題組[271]將大量石墨烯帶進行卷曲隨之縱向切割,便成功的實現了上述想法.通過該實驗可獲得比傳統熱界面材料熱導率高出了兩個數量級的高熱導率界面材料(614.85 W/(m·K)).此外,石墨烯泡沫也是理想的界面材料之一,其具有質輕、高熱導率、高壓縮比等優點.Loeblein等[272]利用金屬鎳泡沫為模板并通過CVD方法在鎳骨架上生長多層石墨烯, 最后將鎳骨架腐蝕清除即得到石墨烯泡沫, 經壓縮其熱導率能夠達到86 W/(m·K).

除了上述材料外,石墨烯纖維[273]、石墨烯壓層材料[206]、石墨烯納米流體[274]等均是較好的基于石墨烯的散熱材料,這些材料可以滿足各種環境下的不同需求.

在二維材料中,氮化硼因高熱導率且表面非常光滑等特點同樣是非常具有潛能的散熱材料.氮化硼還具有一個比較明顯的優點—絕緣,因此它可以與電學器件直接接觸而不必擔心出現電路短路的問題.Choi等[248]通過熱掃描探針SThM掃描石墨烯器件表面溫度, 發現當熱流密度為1600 W/cm2時器件表面溫度變化最大值為42 K.相同功率情況下在器件與襯底之間加上多層氮化硼,器件表面溫度變化最大值則降低了2.2倍,僅為18 K.在硒化鎢器件和硒化鉬器件中,復旦大學魏大程課題組和同濟大學徐象繁課題組[250]也觀察到了類似的現象,如圖19(a)—圖19(f)所示,同時發現在單層氮化硼的輔助下器件的飽和功率得到了一定提高.可以看出單層/多層氮化硼能夠將器件運行所產生的熱量快速且有效的輸送出去,避免“熱點”的出現對器件造成損壞.

本文只提綱挈領介紹二維材料界面熱阻研究進展及其在散熱領域的應用.更多內容可參考相關文獻[23,275].

通過以上介紹,可以看出二維材料在散熱方面的應用主要集中于兩個方向:作為熱擴散材料避免器件中熱量的積聚及充當熱界面材料提高界面熱輸運能力.如在消費電子領域,芯片功耗增大和機身結構變化及小巧化是其發熱的主要原因.在手機芯片方面,4G芯片的功耗為1—2 W,而5G芯片的功耗可高達5—7 W.華為M20X手機以及小米10手機已將石墨烯散熱膜用于熱管理系統中,石墨烯助力的鋰電池也將在手機中推廣,其目的在于快速將CPU或電池工作時產生的熱量導出提高零件的使用壽命和改善用戶使用體驗.與此同時,充當熱界面材料,二維材料的前景還是比較光明的,但是在實際應用之前還需要解決一些技術問題,例如進一步提高其性能、使用壽命、與現有技術之間的融合度等.

圖19氮化硼對硒化鎢以及硫化鉬器件中溫度分布的影響[250]:(a)?(d)SThM溫度掃描圖;(e)器件邊界處溫度變化圖;(f)器件中溫度分布柱狀統計圖Fig.19.Effect of h-BN on temperature distribution in WSe2 and MoSe2 devices [250]:(a)?(d)Temperature scanned by SThM;(e)temperature variation at device boundary;(f)histogram of temperature distribution in devices.

6 總結及展望

綜上所述,本文以二維材料的熱導率為研究平臺來探討微納尺度下熱傳導最基礎的物理問題,如尺度效應、維度效應、界面熱阻等等,并探討調控熱導率及界面熱阻的方法,希望以此對二維材料在熱物理領域特別是散熱研究方向的應用提供實驗基礎.相比于十年前,我們對二維材料熱傳導機理已經有了一定的認識和了解.然而,路漫漫其修遠兮,對二維材料熱傳導的研究仍存在很多瓶頸和問題,但這也可以為二維材料熱傳導相關的進一步研究指明一定的方向:

1)到目前為止,沒有關于二維材料反常熱傳導的嚴格解析解.現存的反常熱傳導模型只局限在二維晶格[11,12,276].二維晶格系統里是沒有面外聲子模式的(即ZA聲子),然而在真實二維材料如石墨烯和氮化硼,面外聲學聲子對熱導率起著決定性的作用[102].

2)石墨烯熱導率是多少?不同的實驗之間存在很大的差異,而三聲子散射和四聲子散射計算結果也不能自洽.公認的是懸空單層石墨烯熱導率比石墨塊體更高,然而最近的實驗顯示石墨塊體/薄片的室溫熱導率達3200—4300 W/(m·K)[90,194].目前采用的熱橋法和拉曼法在測量熱導率時,其樣品表面往往會吸附少量小分子,進而抑制聲子振動.研究人員一般采用退火(約200—300℃)的辦法去除表面雜質,但是由于存在負熱膨脹系數,高溫退火會使得ZA聲子受到抑制從而影響最終實驗結果.同時,懸空大尺寸(如大于50μm)石墨烯用于熱導測量也存在很大的技術瓶頸.以目前掌握的實驗測量技術,測量單層懸空石墨烯本征熱導率似乎是“不可能的任務”.

3)在當前的理論框架里,四聲子散射往往被直接忽略,因為其是只有在高溫區才會逐漸出現的一類聲子散射行為[106].但是有部分理論研究發現即使是在室溫下,單層石墨烯中大量的低能ZA模聲子導致其四聲子散過程是不容忽視的[107,108].因此有必要用四聲子散射理論重新審視二維材料熱傳導行為.

4)二維到三維的維度效應也是一個非常有意義的研究方向.二維材料為熱導率的維度效應研究提供了一個絕佳的平臺.有部分結果顯示,石墨烯和氮化硼的熱導率隨著厚度的增加而降低,并在四層的時候達到和塊體類似的熱導率[44,56,64].但是多厚的二維材料才可以變為三維材料?解決這個問題仍需要大量的實驗工作.

5)雖然有理論工作表明即使當樣品的尺度到了毫米甚至厘米量級仍存在熱導率的尺度效應[174,202],然而目前的實驗中樣品長度最多只有9μm[17].還需要大量的實驗來對理論進行驗證.

6)近期的研究表明石墨塊材中存在聲子流體動力學行為及第二聲,并可解釋石墨塊體/薄片中的高熱導率及熱導率尺度效應[194,195].雖然早期的理論顯示二維材料中也存在聲子流和第二聲[192,193],但是到目前為止沒有任何發表的實驗數據可支持這個論點.

7)目前普遍采用的界面熱阻理論,如AMM模型[251]和DMM模型[252],都是簡單地假設聲子以彈道傳輸或者擴散傳輸的形式通過界面,因此這兩個模型與實驗結果都有一定的差別.而最新理論和實驗顯示,在低維系統中,聲子不是以簡單的彈道或擴散傳輸,而是以超擴散的形式傳輸.由此需要一種新的模型,在考慮界面熱阻時引入超擴散的概念.

8)熱導率測量,如拉曼法及熱橋法,都不可避免地存在接觸熱阻問題,這將大大影響實驗結果.雖然有部分課題組采用雙拉曼激光法[67]和電子束自加熱法[54]以消除接觸熱阻的影響,但是苛刻地實驗條件及昂貴的實驗設備使得大多數課題組無法進行相關實驗.

9)通常采用的界面熱導測量,如TDTR和3w法可以提供微米尺度的空間分辨率,但是它只能用于薄膜材料界面熱阻測量,同時其在面內的空間分辨率也局限于其加熱激光的光斑大小(通常為微米左右).由此,有必要開發一種全新的測量手段,要求其空間分辨率能達到納米尺度,并且可探測二維材料的界面熱阻信息[54,55].雖然電子束自加熱法可用于測量部分材料界面熱阻,但是目前該測量方法局限于掃描電子顯微鏡腔體內,不能進行變溫測量, 也無法進行多物理場調控,如光場, 磁場等[54,55].因此,有必要開發一種新的測量手段,可對結構復雜界面進行熱阻測量,同時兼容商業儀器如變溫強磁系統,進行光、熱、電和磁場等多物理場耦合測量,以獲得更多界面熱阻信息.