改進響應面法在橋梁結構有限元模型修正中的應用

楊雅勛，楊福利，陳 東,2

(1.長安大學 公路學院，陜西 西安 710064; 2.上海市政工程設計研究總院(集團)有限公司天津分公司 天津 300042)

0 引言

采用有限元模型對工程結構分析已成為現在工程設計必不可少的環節。模型建立過程中的多種因素的簡化、截面尺寸誤差、材料性能參數、連續介質離散化的精度及施工過程中某些不確定因素的影響等都會使初始有限元模型計算結果與實測結果存在偏差[1]。因此，務必考慮對初始有限元模型修正，使其與橋梁實際受力性能一致。

國內外已對有限元模型修正進行了一系列的研究，提出了幾種模型修正方法，主要有矩陣修正法、靈敏度法和響應面法等[2]。矩陣修正法將質量矩陣、剛度矩陣作為修正對象對有限元模型進行修正，但復雜結構的矩陣不容易得出，且修正后的矩陣往往不具有稀疏、對稱的性質，喪失了其物理意義[3-5]。靈敏度法對于修正參數選取有較大隨機性和單一性，每次迭代必須調用程序計算，計算量較大，修正效率低[6-8]。響應面法由于其精確性和高效性在優化設計、可靠度分析和有限元模型修正中得到廣泛應用[9-11]。

本研究對傳統響應面法進行改進，并將改進后響應面法應用到一座系桿拱橋的有限元模型修正中，以鋪裝層的厚度及各構件的彈性模量和密度為待修正參數，采用F檢驗法尋找顯著性高的參數，通過函數擬合構造響應面模型，再根據試驗數據，在響應面內優化求解，得到最優解對有限元模型進行修正。在響應面法的基礎上，利用成橋荷載試驗數據對一座系桿拱橋模型進行修正，修正前后誤差明顯降低，驗證了該方法在系桿拱橋模型修正中的有效性。

1 基于響應面法的有限元模型修正理論

1.1 修正參數及響應參數的選取

通常選擇材料的彈性模量、密度、泊松比阻尼比、摩擦系數、支座剛度等作為待修正參數。當基于動力測試數據對模型進行修正時，響應值通常為模態振型和模態頻率，當基于靜力測試數據對模型進行修正時，響應值通常為撓度和應變。

1.2 試驗設計與參數顯著性檢驗

以有限的試驗次數獲得最有效的試驗數據的關鍵在于試驗設計，樣本數據的增加能夠使模型的精確度提高，但大量的數據會使計算效率顯著降低[12]。因此，在不影響精度的前提下，選擇最具代表性的樣本數據是試驗設計的中心原則。D-最優設計是一種基于最小化協方差矩陣|(X′X)-1|的計算機隨機生成的設計，在擬合響應面模型時，其樣本個數為n=(k+1)(k+2)/2(k為待修正參數的數量)，與其他試驗設計相比，具有較高的精度且試驗次數少[12]。

參數顯著性檢驗是對參數響應值進行方差分析，結合F檢驗法，挑選顯著性高的參數。其基本原理是將總離差平方和分解為由各個試驗因素引起的離差平方和SSA和試驗數據本身偏差引起的離差平方和SSE，然后，構造服從F分布的統計量FA：通過計算出的FA值進行假設檢驗，判定參數的顯著性。

統計量：

(1)

式中，dA為因素自由度數，dE為偏差自由度數。在方差分析中，對于給定的顯著性水平α，當F≥F1-α(nc,ne)即P≤α時，則稱該因素對其影響顯著；否則，該因素對響應值的影響不顯著。

1.3 改進響應面法

對于修正參數較多，輸入值和響應值之間存在高度非線性的問題，傳統響應面法構造的響應面模型往往精度不高，所以更適合局部模型的建立，而徑向基函數的方法可用于全局顯式模型的建立[13]。改進響應面法是將二階多項式與徑向基函數相結合作為響應面的模型函數,旨在提高模型與實際結構在參數取值的全局范圍內的契合度，提高模型修正的精度。

根據最佳一致理論中的哈文條件的等價定義[14]，徑向基函數是未知函數唯一的最佳一致逼近形式[13]。根據不同的徑向基函數的函數近似結果，發現對不同類型的測試函數、高斯函數的均方根誤差均較小，說明高斯徑向基函數具有良好的擬合適應性、較高的精度和應用的廣泛性[15]。所以，選擇高斯函數作為徑向基函數，隨著空間維數的增加，計算量呈線性增長，對模型的非線性模擬適應能力強[16-19]。因此,將多項式函數和徑向基函數相結合作為響應面函數，形成混合響應面[20-23]，即改進響應面法。

傳統響應面法一般選用二階多項式作為響應面模型函數式[24]，其函數形式如式(2)；對傳統響應法進行改進，在二階多項式后增加高斯函數項，旨在提高響應面擬合精度，其方程形式如式(3)：

(2)

(3)

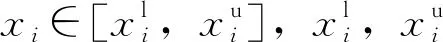
文獻[13]通過大量的數值算例驗證，總結出σ取值的經驗公式：

(4)

式中r0為設計空間內最遠兩點的距離。

檢驗響應面擬合程度可靠性的標準有：

(5)

(6)

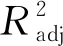
1.4 優化求解

構造目標函數對響應面模型進行優化求解[25]。目標函數表達式如式(7)：

(7)

式中，fi為響應面模型的計算值，fii為結構的實測值。在參數取值區間內，當目標函數F取最小值時，得到參數最優解，即修正后的參數取值。

2 有限元模型修正

2.1 工程概況與有限元模型建立

貴州岑鞏黃弓大橋為(52+70+52) m的三跨系桿拱橋，拱軸線為二次拋物線，主拱矢高14 m。主拱圈和縱梁均為2 m×1.2 m的矩形截面，中橫梁為1.35 m×0.8 m的矩形截面，橫撐為1.2 m×1 m的內八角形箱形截面，均為鋼筋混凝土材料；吊桿采用消除預應力鍍鋅高強鋼絲束。材料參數見表1。根據橋梁的結構信息，采用ANASYS建立主橋的有限元模型如圖1所示。

表1 材料參數Tab.1 Material parameters

圖1 黃弓大橋有限元模型Fig.1 Finite element model of Huanggong Bridge

2.2 靜動載試驗2.2.1 靜載試驗

按照作用效應等效的原則進行荷載試驗，獲得主拱圈跨中和縱梁跨中各測點的數據。為保證其合理有效性，按影響線的最不利位置進行加載，并保證各截面的加載效率在0.95～1.05之間，本次靜載試驗共采用4輛35T的三軸加載車，設置4個工況：

(1)工況1：L/2拱肋、縱梁截面最大正彎矩中載工況；

(2)工況2：L/2拱肋、縱梁截面最大正彎矩偏載工況。

(3)工況3：L/4拱肋、縱梁截面最大正彎矩中載工況；

(4)工況4：L/4拱肋、縱梁截面最大正彎矩偏載工況。

荷載試驗中應變和撓度測點布置圖如圖2所示，現場實驗如圖3所示。測試多組數據取平均值并進行處理，消除沉降影響，由于殘余應變和殘余撓度在合理范圍內，消除殘余應變和殘余撓度，得到各工況下的應變和撓度測試數據見表2。

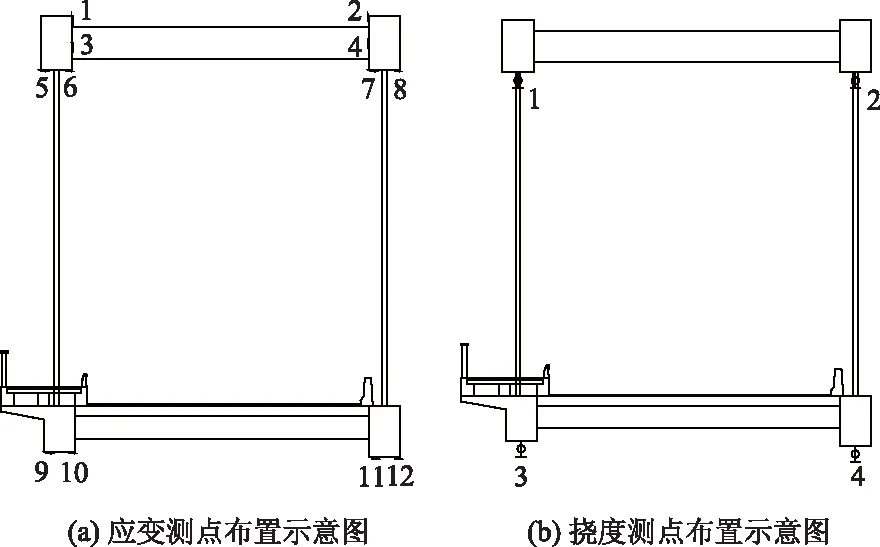
圖2 荷載試驗測點布置示意圖Fig.2 Schematic diagram of arrangement of measuring points in load test

圖3 現場荷載試驗Fig.3 Field load test

表2 靜載試驗應變值Tab.2 Strain values in static load test

表3 靜載試驗撓度值Tab.3 Deflection values in static load test

2.2.2動載試驗

采用行車激勵的方法對橋梁進行動力測試，使用加速度傳感器進行數據收集。在主橋的拱肋L/2截面和橋面L/2截面的拱肋上緣和橋面分別布置測點，測試結構振動頻率。以一輛35T的激勵車分別以15，30，45 km/h速度對橋梁進行激勵，采集多組數據并進行處理，對比個階模態對數據進行處理后得到各階頻率實測值，并將實測值與計算值對比見表4。

表4 自振頻率對比Tab.4 Comparison of natural frequencies

2.3 有限元模型修正2.3.1 修正參數及響應值選取

對本橋結構特點進行分析，得出可能造成模型與實橋存在偏差的因素有：材料特性參數、幾何尺寸，邊界條件等。研究中模型是根據施工圖建立的，截面幾何尺寸誤差較小，橋墩與縱梁簡支連接，橋墩變形對頻率響應影響較小，但施工過程中標高控制誤差的存在會使成橋后的橋面鋪裝層厚度產生誤差，以材料參數和橋面鋪裝層厚度作為修正對象，在設計值上下20%內進行取值，參數及修正范圍見表5。

表5 模型修正參數選取Tab.5 Model correction parameter selection

2.3.2試驗設計與參數顯著性分析

根據實橋的結構特點與本次模型修正的目的，選擇工況1作用下拱頂截面撓度d1，d2,縱梁跨中撓度d3，d4及前三階頻率f1，f2，f3作為響應值進行試驗設計。由于待修正參數較多，按照取最少樣本點獲得最有效的數據原則，選擇D-最優準則的計算機生成設計。試驗設計得到65個(55個設計試驗點+5個不匹配點+5個最佳重復點)隨機樣本點見表6，將樣本點數據代入有限元模型得到響應值見表7，并進行方差分析。根據各參數類型及其對應顯著水平值得顯著性分析圖，如圖4所示：

表6 D-最優試驗設計參數Tab.6 D-optimal test design parameters

表7 D-最優試驗設計響應值Tab.7 D-optimal test design response values

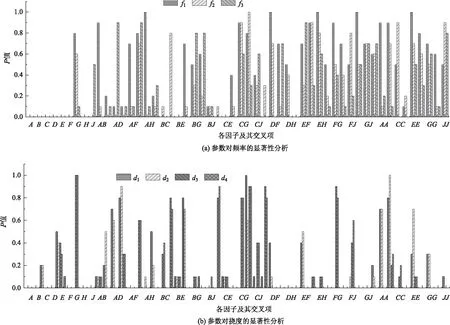
圖4 參數顯著性分析Fig.4 Parameter significance analysis

本次分析中設置顯著性水平為0.05，當p∈[0,0.001]時，該參數影響高度顯著；當P∈(0.001,0.05]，該參數影響顯著；當P∈(0.05,1]時，該參數影響不顯著。參數對頻率的顯著性分析結果表明，主效應中E1，D1，E2，D2對前三階頻率影響高度顯著，E3，D3，E4對前三階頻率影響顯著；大部分參數交互項和二次項對前三階頻率影響不顯著。參數對撓度的顯著性分析結果表明，主效應中彈性模量對撓度影響高度顯著；部分參數的交互作用對撓度影響顯著，主要為各構件彈性模量交互項；縱梁彈性模量二次項,縱梁密度二次項對撓度影響高度顯著，其他二次項分別對d1，d2，d3，d4的顯著性有不同程度的影響。橋面鋪裝層厚度對撓度影響高度顯著，分析原因，主要為鋪裝層層厚度在一定程度上改變了橋梁的整體剛度。

圖5 部分響應面模型Fig.5 Partial response surface models

2.3.3響應面擬合

2.3.4優化求解

將設計參數代入響應面模型得到計算值，構造計算值與實測值目標函數并進行優化求解，采用粒子群優化算法求解，得到修正后的參數見表9。將修正后的全部參數代入有限元模型計算，得到頻率和撓度的計算值并與實測值進行對比見表10。

表8 響應面精度檢驗Tab.8 Response surface accuracy test

表9 優化求解后的參數Tab.9 Parameters after optimization

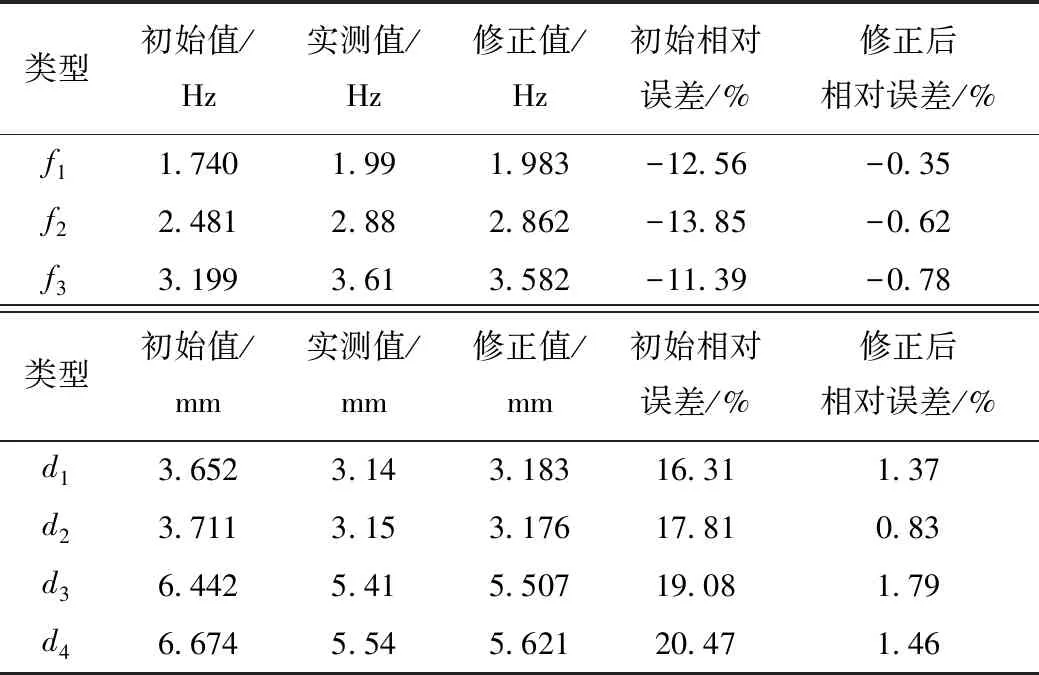
表10 工況1修正前后響應值對比Tab.10 Comparison of response values before and after correction of working condition 1

由表9可以發現，有限元模型修正后，各構件的彈性模量均增大，吊桿的彈性模量較初始值增加了0.065倍；拱肋、縱梁、橫梁的彈性模量值較初始值都增加了0.14倍以上；鋪裝層厚度比初始值增加了約0.04倍，拱肋的密度較初始值則減少了0.09倍，其余各構件密度較初始值變化不大，均在0.03倍之內。分析原因可能為：(1)拱肋結構、縱梁、橫向聯系中鋼筋的存在增大了構件的彈性模量，而初始有限元模型中未考慮鋼筋的影響；(2)施工中使用的水泥或者混凝土標號高于設計值；(3)拱肋澆注過程中振搗不完全，造成密實度降低。修正后的彈性模量可視為各鋼筋混凝土構件的整體彈性模量，反映了各構件的實際剛度。

由表10可以發現，修正后的頻率響應值誤差由初始的13%左右降到1%以內，修正后的撓度響應值誤差由20%降至1.8%以內，在可接受的范圍內。結果表明：響應面法可以實現對系桿拱橋結構有限元模型修正，且精度能滿足工程要求。

2.3.5結構靜動力響應驗證

將原有限元模型中的參數改為修正值，計算不同工況下的響應值，并與實測值對比，圖6表明，修正后的有限元模型響應值與實測值偏差明顯降低。

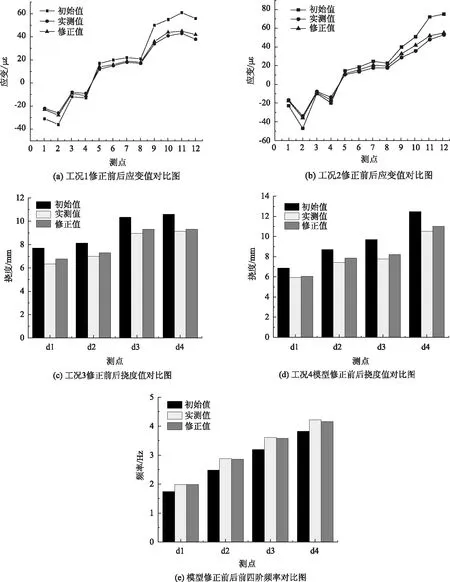
圖6 模型修正前后計算結果對比圖Fig.6 Comparison of calculation results before and after model correction

3 結論

以貴州岑鞏黃弓大橋為例，結合靜動力測試數據，采用改進響應面法，對該橋的有限元模型進行了修正，得到以下幾點結論：

(1)利用統計學原理，結合徑向基函數，將傳統響應面法進行改進，增加了對模型非線性模擬的適應性，提高了響應面的擬合精度。基于靜動力測試數據在響應面內優化求解，以修正參數進行D-最優試驗設計，避免了采樣點的主觀性，降低了樣本點采集數量，提高了樣本點質量；縮減有限元模型的調用頻率，模型修正的效率提高。

(2)建立了貴州岑鞏黃弓大橋有限元模型，結合靜動力測試數據得到對撓度的主要響應因素為彈性模量E二次項效應，并將鋪裝層厚度作為修正參數，分析得出鋪裝層厚度對頻率影響不顯著，對撓度影響高度顯著。因此，在今后的分析中鋪裝層厚度對橋梁的靜力特性的影響不可忽略。

(3)利用改進的響應面法修正后的系桿拱橋有限元模型，其計算值更接近于實測值，頻率誤差由原來的13%左右降至1%以內，撓度誤差由原來的20%左右降至1.8%以內，在結構靜動力響應驗證中，修正后有限元模型的響應值與實測值相吻合，為以后的橋梁結構受力性能再分析、承載能力評估等提供了基準有限元模型，對橋梁服役期內的健康監測與結構損傷識別具有重要意義與實用價值。