基于Octave的射頻濾波器理論建模與設(shè)計(jì)

余景原，王子瑋，許國泰

(上海市信息網(wǎng)絡(luò)有限公司，上海 200081)

0 引言

作為無線通信系統(tǒng)中必不可少的射頻端組件，射頻帶通濾波器(Bandpass Filter，BPF)[1]的設(shè)計(jì)開發(fā)成為關(guān)系到整個(gè)射頻端乃至整個(gè)無線系統(tǒng)開發(fā)成功與否的重要環(huán)節(jié)。通常對(duì)于頻率低于1 GHz的射頻濾波器可以采用基于電感(L)、電容(C)等集總參數(shù)元件的歸一化低通濾波器(Lowpass Filter，LPF)作為原型(Prototype)進(jìn)行設(shè)計(jì)[1-2]，但由于集總參數(shù)元件的頻率限制，對(duì)于藍(lán)牙[3]、WLAN[4]、WiFi[5]等工作在微波射頻頻段(2.4 GHz)的無線通信系統(tǒng)而言，通常無法使用集總參數(shù)原件，而必須使用微帶線、波導(dǎo)等分布參數(shù)傳輸線來構(gòu)造實(shí)際濾波器[6]。因此，即使可以使用傳統(tǒng)的濾波器設(shè)計(jì)理論獲得集總參數(shù)原件L和C的理論值，也無法直接用于分布參數(shù)射頻帶通濾波器的設(shè)計(jì)，必須推導(dǎo)分布參數(shù)的電路模型。

與集總參數(shù)電路不同，在設(shè)計(jì)分布參數(shù)諧振器等電路時(shí)使用的主要參數(shù)是諧振頻率，諧振器間的耦合系數(shù)，以及電路輸入/輸出端口處的外部Q值[1-6]。文章從傳統(tǒng)的基于集總參數(shù)濾波器模型出發(fā)，建立一個(gè)基于各個(gè)諧振器的諧振頻率，諧振器間的耦合系數(shù)以及外部Q值的射頻濾波器模型。通過推導(dǎo)給出這些分布參數(shù)與傳統(tǒng)濾波器設(shè)計(jì)理論中的歸一化低通原型濾波器參數(shù)(L和C)的關(guān)系。為了擺脫復(fù)雜煩瑣的公式推導(dǎo)，在建模(公式推導(dǎo))中選用了一種在斯坦福大學(xué)的機(jī)器學(xué)習(xí)課程中被推薦的，功能上幾乎等同于Matlab[7-8]的開源免費(fèi)科學(xué)計(jì)算軟件Octave[8-9]。歸功于其強(qiáng)大的數(shù)值和符號(hào)計(jì)算功能，有效提高了設(shè)計(jì)速度和效率。論文在給出基于Octave的具體推導(dǎo)過程的同時(shí)，也給出了可用于2.4 GHz無線通信系統(tǒng)的發(fā)夾型微帶濾波器的設(shè)計(jì)實(shí)例。通過仿真結(jié)果與實(shí)測結(jié)果的比較來驗(yàn)證模型以及仿真設(shè)計(jì)過程的有效性。

1 基于Octave的射頻帶通濾波器的理論建模與綜合設(shè)計(jì)

1.1 基于集總參數(shù)LC的低通原型濾波器

由于射頻帶通濾波器模型需要從傳統(tǒng)的濾波器模型開始推導(dǎo)，首先介紹傳統(tǒng)的基于集總參數(shù)LC的歸一化低通原型濾波器。圖1中給出了一個(gè)由并聯(lián)C開始，串聯(lián)L和并聯(lián)C交替連接構(gòu)成的階梯狀電路。在輸入端1-1’接入電源和電源電阻R0，在輸出端2-2’接入負(fù)載電阻Rn+1后就可以構(gòu)成2端口網(wǎng)絡(luò)。根據(jù)電路理論[1-2]可知，此2端口網(wǎng)絡(luò)具有低通頻率特性，我們把這樣的電路作為歸一化低通濾波器的原型電路。其中，把包括輸入輸出端電阻在內(nèi)的所有電路元件從左到右順次用gi(i=0～n+1) 來表示。其中，gi的值可根據(jù)希望實(shí)現(xiàn)的濾波器種類來選取。比如，若要實(shí)現(xiàn)等波紋(切比雪夫)濾波器，其理論傳遞函數(shù)(S21)和理論反射系數(shù)(S11)由(1)給出

(1)

(2)

β=ln[coth[0.25·ln(1+ε2)]],γ=sinh[β/(2n)]

(3)

1.2 基于串聯(lián)L和K變換器的低通原型濾波器

為了獲得適用于分布參數(shù)濾波器設(shè)計(jì)的模型，作為過渡模型，從圖1的傳統(tǒng)模型開始，繼續(xù)推導(dǎo)一種基于串聯(lián)L和K變換器的低通原型濾波器。圖2(a)中給出2端口網(wǎng)絡(luò)元件K變換器[1-2]的ABCD矩陣。經(jīng)過簡單的推導(dǎo)可以知道，若在K變換器的端口2處連接負(fù)載ZL，在端口1的輸入端所看到的輸入阻抗則為Zin=K2/ZL。因此，若K為實(shí)數(shù)，ZL為電容性元件，則Zin轉(zhuǎn)換為等效的電感性元件，反之亦然。即，K變換器可應(yīng)用于電容性元件和電感性元件之間的等效轉(zhuǎn)換。圖2(b)中給出了利用串聯(lián)電感L和兩個(gè)K變換器來等效并聯(lián)電容C的等效變換。應(yīng)用圖2(a)中的等效變換，把圖1中的所有并聯(lián)電容用串聯(lián)電感L和K變換器替代后，可得到圖3中的基于串聯(lián)L和K變換器的低通原型濾波器模型。為了獲取圖3與圖1中的電路模型之間的各元件值之間的對(duì)應(yīng)關(guān)系，需要進(jìn)行公式推導(dǎo)，對(duì)于這個(gè)煩瑣的過程，借助Octave的符號(hào)運(yùn)算功能[8]。以下給出推導(dǎo)過程。

圖1 基于集總參數(shù)LC的階梯狀電路的歸一化低通

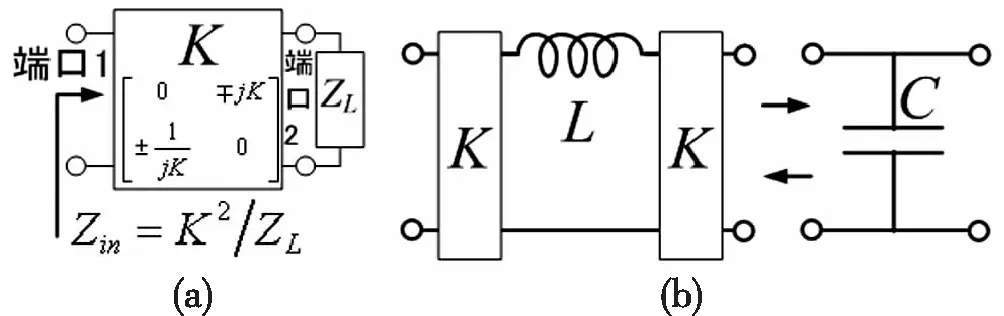
(a) K變換器的ABCD矩陣及阻抗變換特性

圖3 基于串聯(lián)L和K變換器的低通原型濾波器

%

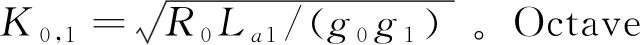
syms W R0 g0 g1 La1 Z22 Z12 K01 La1 real%定義變量

Y11 = (1/Z22 + j*W*g1)/g0 %計(jì)算圖1中的Y11

Y01=1/( K01^2/ (Z12+j*W*La1)*R0) %計(jì)算圖3的Y01

eq1 = real( Y11 ) - real( Y01 ) %建立實(shí)部方程

eq2 = imag( Y11 ) - imag( Y01 ) %建立虛部方程

[KK01] = solve(eq2 == 0, K01) %求解虛部方程eq2

%

%

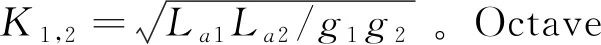
syms Y33 Z23 g2 K12 La2 real %定義實(shí)數(shù)變量

vK01 = KK01(2) %把K01的結(jié)果保存在vK01中

ZZ22 = 1/Y33 + j*W*g2 %計(jì)算圖1的Z22

ZZ12 = K12^2/(Z23+j*W*La2) %計(jì)算圖3的Z12

eq3=real(subs(eq1, {Z22,Z12,K01},{ZZ22,ZZ12,vK01}))

eq4=imag(subs(eq1, {Z22,Z12,K01},{ZZ22,ZZ12,vK01}))

[KK12, ZZ33] = solve(eq3 == 0, eq4 == 0, K12, Z33)

%求解方程組獲得K12和Z33

%

通過相似的推導(dǎo)過程，可以獲得圖3中的低通原型濾波器的K變換器的K值與圖1種的原型低通濾波器的元件值的關(guān)系式。

(4)

其中R0，Rn+1，Lai可以任意選擇。這里由于使用Octave進(jìn)行推導(dǎo)，使得原來煩瑣的推導(dǎo)過程變得非常容易。

1.3 利用頻率變換獲得帶通濾波器理論模型

設(shè)計(jì)帶通濾波器時(shí)，需要通過對(duì)低通原型濾波器模型進(jìn)行頻率變換來獲得帶通濾波器的理論模型。在具體操作上，需對(duì)低通原型濾波器的理論特性(1)(2)中的歸一化頻率用以下公式代換[1]。

(5)

由于圖3中僅有串聯(lián)L的阻抗與頻率有關(guān)，在對(duì)原型濾波器進(jìn)行頻率變換時(shí)，僅需要把其中的串聯(lián)L替換成串聯(lián)LC諧振電路。帶通濾波器的電路圖在圖4中給出，元件值由下式給出：

(6)

1.4 射頻帶通濾波器的理論建模

在1.1中已經(jīng)指出，由于射頻濾波器的實(shí)現(xiàn)需使用分布參數(shù)元件，因此為了推導(dǎo)出適合于射頻帶通濾波器的模型，需要把圖4中的集總參數(shù)L，C，K轉(zhuǎn)化成諧振器的諧振頻率f0，諧振器間的耦合系數(shù)kij，以及端口處的外部Qe值。

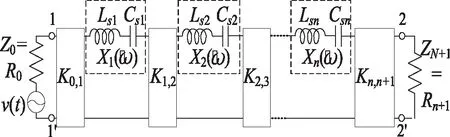
圖4 基于K變換器和串聯(lián)LC電路的帶通濾波器

從圖4可知，第i個(gè)串聯(lián)LC諧振器的電抗參數(shù)Xi(ω)可以由下式給出：

(7)

定義如下電抗斜率參數(shù)(reactance slope parameter)

(8)

把(8)代入(4)，可以獲得如下的Ki,j計(jì)算公式：

(9)

其中R0，Rn+1，χi(i=1,...,n)可以取任意數(shù)值。

圖5(a)給出了耦合串聯(lián)LC諧振器與K變換器的等效變換，圖5(b)給出了包含K變換器和電源部分的串聯(lián)LC諧振器等效電路。把圖5(a)(b)的等效變換應(yīng)用于圖4的電路，可以獲得圖5(c)的基于諧振頻率f0，外部Qe, 諧振器間的耦合系數(shù)kij的帶通濾波器模型。通過簡單推導(dǎo)可獲得以下設(shè)計(jì)公式：

(10)

以上公式推導(dǎo)都通過Octave完成，由于和前面給出的程序例相似以及篇幅原因，這里不再贅述。

2 設(shè)計(jì)實(shí)例及分析

為了驗(yàn)證圖5中給出的用Octave導(dǎo)出的射頻帶通濾波器理論模型以及相應(yīng)公式的正確性，應(yīng)用這個(gè)模型設(shè)計(jì)了一個(gè)用于2.4GHz頻段(藍(lán)牙，無線WiFi，車輛警報(bào)器系統(tǒng)等通信系統(tǒng)所利用的頻段)[3-5]的帶通濾波器。所設(shè)計(jì)濾波器的中心頻率為2.45GHz，相對(duì)帶寬為11.2%。具體設(shè)計(jì)步驟如下：

(1)選擇9階切比雪夫函數(shù)作為帶通濾波器的理論目標(biāo)函數(shù)。把n = 9代入(2)和(1)，選擇波紋系數(shù)=0.107(0.05dB)獲得低通原型濾波器的理論特性。然后應(yīng)用(5)中給出的頻率變換公式，選擇中心頻率f0=2.45GHz，相對(duì)帶款FBW=0.112，便可獲得所需設(shè)計(jì)的帶通濾波器的理論特性(圖7中的直線)。為了方便讀者，在附錄中給出了基于Octave的帶通濾波器理論特性的計(jì)算程序，并給出必要的說明。

圖5 射頻帶通濾波器的建模

(2)使用圖6中給出的微帶發(fā)夾型濾波器結(jié)構(gòu)來設(shè)計(jì)帶通濾波器。由于要實(shí)現(xiàn)9階切比雪夫?yàn)V波器，需要9個(gè)發(fā)夾型諧振器，在輸入和輸出端，選用平行耦合線結(jié)構(gòu)。濾波器的等效電路在圖5(c)中給出，所有的諧振器的諧振頻率都設(shè)定為濾波器的中心頻率f0=2.45 GHz，輸入端和輸出端的外部Qe值以及第i和i+1個(gè)濾波器之間的耦合系數(shù)ki,i+1(i= 1，…，8)可由(10)獲得，其中g(shù)i(i=0，…，10)需通過(3)獲得(n=9)。

圖6 9階切比雪夫發(fā)夾型微帶濾波器的實(shí)物圖

(3)選擇介電常數(shù)2.2，厚度0.787 mm的基板設(shè)計(jì)實(shí)際的微帶濾波器。根據(jù)步驟(2)中所獲得的外部Qe以及耦合系數(shù)ki,i+1(i= 1，…，8)，可以獲得濾波器的物理尺寸的初值，然后通過電磁場仿真軟件[9-10]進(jìn)行優(yōu)化，從而獲得最終的尺寸。由于軟件仿真優(yōu)化偏離文章主題以及篇幅的限制，對(duì)這一部分的說明予以省略。最后通過蝕刻(etching)工藝實(shí)際制作濾波器。圖6中給出了實(shí)物照片。然后使用網(wǎng)絡(luò)分析儀測量S參數(shù)，并在圖7中與理論特性進(jìn)行比較。

圖7 圖6中的切比雪夫?yàn)V波器的理論特性與實(shí)測結(jié)果的比較

從圖7中可以得到以下結(jié)論：(1)實(shí)驗(yàn)結(jié)果和理論結(jié)果較好地吻合，證明了使用Octave推導(dǎo)出的射頻濾波器模型以及綜合設(shè)計(jì)公式是有效的。(2)實(shí)測結(jié)果的帶通特性具有2 dB左右的插入損耗，這主要是由所使用基板的介電材料的損耗以及金屬(銅)損耗而引起的。(3)可以發(fā)現(xiàn)實(shí)測結(jié)果的阻滯特性與理論特性存在一些差異，由于誤差主要發(fā)生在-50 dB以下的區(qū)域，推測是由于電路的制造誤差以及測量誤差所造成的。另外必須應(yīng)該指出，由于阻滯特性好于-50 dB，即使和理論特性存在誤差，也完全不影響濾波器的實(shí)際使用性能。

3 結(jié)語

文章使用與Matlab具有相似功能的免費(fèi)開源科學(xué)計(jì)算軟件Octave，推導(dǎo)出適合于設(shè)計(jì)基于分布參數(shù)射頻帶通濾波器的電路模型以及相應(yīng)的綜合設(shè)計(jì)公式，給出了基于Octave的詳細(xì)推導(dǎo)過程，并附上源程序。為了驗(yàn)證導(dǎo)出的模型以及綜合公式的有效性，筆者設(shè)計(jì)了一個(gè)9階切比雪夫梳發(fā)夾型微帶濾波器，并做了實(shí)驗(yàn)。實(shí)驗(yàn)結(jié)果和理論結(jié)果吻合得較好，從而證明了推導(dǎo)出的理論模型以及綜合設(shè)計(jì)方法以及Octave作為計(jì)算工具的有效性。

另外，由于Octave的強(qiáng)大功能，使得公式推導(dǎo)以及濾波器的綜合設(shè)計(jì)過程變得非常方便、快速，大大提高了設(shè)計(jì)效率，降低開發(fā)成本，有效縮短了開發(fā)周期。相信Octave可以被廣泛應(yīng)用于更多的工程設(shè)計(jì)領(lǐng)域。

附錄：圖7中的切比雪夫?yàn)V波器的理論特性的Octave計(jì)算程序

%運(yùn)行以下Octave程序需要安裝GNU Octave以及symbolic package。具體安裝過程請(qǐng)參見參考文獻(xiàn)[8]。

%

pkg load symbolic %加載符號(hào)運(yùn)算模塊

n=9; %設(shè)定切比雪夫?yàn)V波器的階數(shù)

epr=0.10761; %設(shè)定波紋系數(shù)

ff=-5:0.001:5; %低通原型濾波器的頻率范圍

ww=ff.*(2*pi); %角頻率范圍

Wc=1; %低通原型濾波器的截止角頻率

wc1=2.32*2*pi; wc2 = 2.61*2*pi; %把所設(shè)計(jì)的帶通濾波器的截止頻率2.32 GHz和2.61 GHz轉(zhuǎn)化成角頻率

w0=(wc1*wc2)^0.5; %設(shè)定中心角頻率(公式(5))

FBW=(wc2-wc1)/w0; %設(shè)定相對(duì)帶寬(公式(5))

WW=Wc./FBW.*(ww./w0-w0./ww);%LPF->BPF變換公式(公式(5))

Hs=epr*(cos(n*acos(WW))); %濾波器的切比雪夫理論傳遞函數(shù)(式(2))

s21_2=(1./(1+(abs(Hs).^2))); s11_2=(1-s21_2); %式(1)

ls21=10.*log10(s21_2); ls11=10.*log10(s11_2); % dB

plot(ff, ls21,ff, ls11); %繪制濾波器的理論曲線

axis([2 3 -60 0]); %x，y軸的范圍設(shè)定

title(‘BPF’); %添加圖像標(biāo)題

xlabel(‘Frequency(Hz)’); %添加x軸標(biāo)題

ylabel(‘|S21|&|S11|(dB)’); %添加y軸標(biāo)題

legend(‘S21’,‘S11’); legend(‘Location’,‘northwest’) %設(shè)置圖例

set(gca, “fontsize”, 20) %設(shè)置字體大小

%