基于 C-SVM 分類器對影響乘客選擇出行方式的模型建立與求解

楊佳凝

(江蘇大學，江蘇 鎮江 212013)

1 購票行為分析

本文根據 2019 年某高校本科生寒假回程購票信息調查表所給出的 161 組學生購票情況數據和因素調查、該高校本科生另一組回程信息調查表所給出的 85 組購票因素調查，篩選影響購票結果的主要因素，建立購票結果與影響因素之間的數學模型，對影響因素與影響因素之間的關系進行量化分析，從高到低排序，并預測下一年寒假每個學生的購票行為[1]。模型流程如圖1所示。

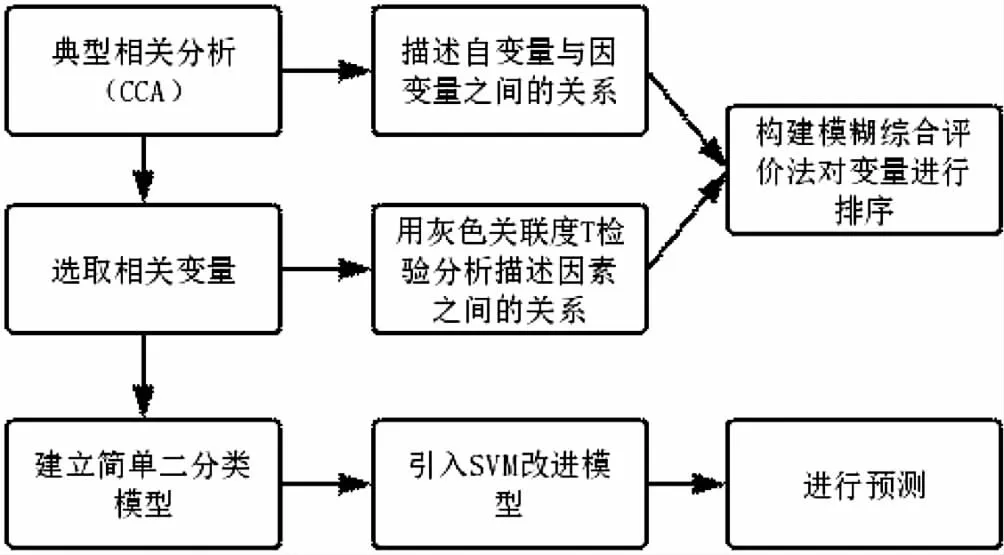
圖1 模型流程

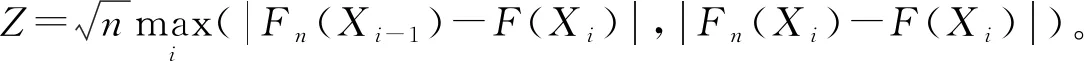
其次，考慮邏輯數據的分布情況。由于邏輯數據只有 0 和 1 兩種狀態，故檢驗其是否呈伯努利分布。令Fn等于伯努利分布函數，進行Kolmogorov-Smirnovtest，發現所有邏輯數據均不成伯努利分布[2]。

2 購買火車票和高鐵票的主要因素

篩選購買火車票和購買高鐵票的主要因素，并建立典型相關分析模型，先建立多元線性回歸模型：

ym=β0+β1X1+β2X2+β3X3+β4X4β5X5β6X6+β7X7+β8X8

典型相關分析函數的因變量為人們選擇購買高鐵票還是普通火車票，自變量分別為影響人們出行的各個因素，即里程長度X1、時間X2、被迫選擇X3、可支配收入X4、購票方式X5、購票價格X6、舒適程度X7以及時間成本X8。

其中，β0表示多元回歸統計常數，β1，……，β8分別代表各個因素的權重。

由表1可知，系數越大，該自變量對因變量的影響程度越大，將這些系數所占的權重從高到低排序可知影響乘客購票行為的主要因素，其中，最主要的因素為兩種交通工具的舒適程度，所占權重為0.046 6；次要因素為購票方式(自付或家庭報銷)，所占權重為0.045 5；排在第3位的因素為行駛時間長度，所占權重為0.036 8。

對于典型相關分析模型(CCA)進行顯著性檢驗，記H(0)=0，表示原假設結果為真。經檢驗得知，顯著性誤差檢驗結果為 46 個，占比為 25%，在誤差允許范圍之內[3]。

表1 典型相關分析模型系數

將數據經過標準化處理后，運用sgn分類函數，經過 CCA 分析可以得到乘客購票行為(購買火車票還是高鐵票)對各個自變量影響程度的大小，篩選出影響乘客購買高鐵票還是火車票的主要因素，在對主要因素進行多元線性回歸后，利用 sgn 函數進行二分類。為進一步刻畫出乘客購買火車票還是購買高鐵票的特征，需要對結果進一步分析，建立數學模型，將每位學生的特征標簽化，將不同的標簽賦予權重后，對學生購買火車票還是高鐵票的行為進行分類，建立數學模型函數表達式為：y=sgn(βX)。

通過sgn符號函數分類，可將在[-1,0]上的數全部映射成-1(乘客購買火車票)，將[0,1]上的數全部映射成1(乘客購買高鐵票)。由此建立出影響乘客購票行為因素的準則并通過回歸分析驗證該模型的準確性。

3 因素與因素之間的量化行為分析

進一步量化分析因素與因素之間的關系，建立一個簡單的二分類模型，用最小二乘法擬合其參數。但是驗證后發現，擬合的準確率較低，為 84.47%。故而，需要優化二分類函數的線性部分，提高其準確率。本團隊通過時間的角度加以分析。最后，建立模糊綜合評價法，對影響乘客購票行為的因素從高到低進行排序。

那么，只需求出min‖Y-Y′‖2，即min‖Aβ-Y‖2。考慮到Aβ-Y是正規方程，用最小二乘法即可得出全局最優解，即β=(ATA)-1ATY，因此，得到簡單二分類模型：

將原始數據Y代入，發現其預測錯25個，準確率為84.47。

簡單二分類的預測結果并不令人滿意，故選擇更換二分類函數的線性部分。考慮到這部分是一個超平面，且是通過歐式距離計算平面與數據點的距離[4]。

將歐式距離優化為幾何距離，引入 SVM 的模型架構，SVM 的超平面如圖2所示。選擇 C-SVM 分類器，其是二分類支持向量機，通過設訓練集、選取合適的核函數K(x,x′)和適當的參數C，構造并求解最優問題，通過設立計算閾值并構造決策函數：

該模型的重點在于調節核函數和參數C。接下來，結合Matlab軟件，對模型進行解算。

圖2 SVM的超平面

將數據按1∶4劃分為訓練集和測試集，核函數選取線性核函數K(x,x′)=xTx，參數C定為6。訓練完畢后得到準確率為96.610 2%。Box可視化圖如圖3所示，測試樣本準確圖如圖4所示。

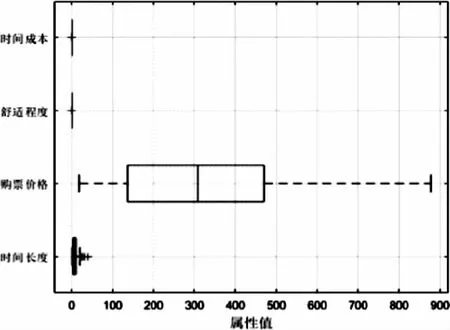
圖3 Box可視化圖

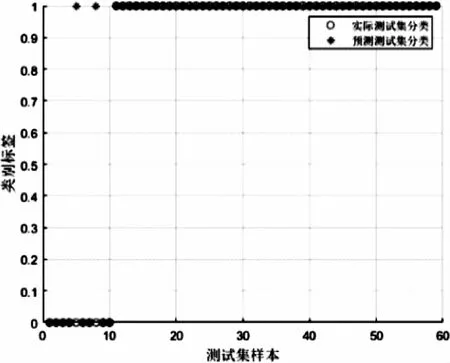
圖4 測試樣本準確圖

本研究希望能通過不同的角度來考察自變量與自變量之間的關系，因此，用灰色關聯度 T 檢驗分析對影響乘客購票行為的自變量關系。考慮到 T 檢驗是關于時間變化的，所以，將 Excel 表格數據按照乘客購買火車票還是購買高鐵票的行為按照時間長度進行分類排序，再根據 CCA 方法，篩選出的4個主要因素時間長度、購票價格、舒適程度和時間成本，并加以分析。其中，時間長度為因變量，其余3個因素為自變量，主要分析自變量與因變量之間的關系。

灰色關聯度 T 檢驗分析的基本思想為按照因素的時間序列曲線和相對變化勢態的接近程度來計算關聯度，對于離散時間序列，所謂兩曲線的相對變化勢態的接近程度，是指兩時間序列在對應各時段Δtk=tk-tk-1(K=2,3,...,n)間各變量經標準化后的增量大小來判定的。若在時間段Δtk間兩增量相等或接近于相等，則這兩時間序列在時段Δtk間的關聯系數就越大，反之就小。兩時間序列的關聯度定義為：各時間段Δtk間的關聯系數的加權平均數，權數為Δtk。

通過Matlab計算得到，在選擇乘坐高鐵的乘客中，時間長度對購票價格、舒適程度和時間成本的關聯度為-0.035 9，0.011 2和0.007 9。在選擇乘坐火車的乘客中，時間長度對購票價格、舒適程度和時間成本的關聯度為-0.011 3，-0.009 3 和 0.030 5。很明顯，時間長度對于其他3個變量的影響對于乘客購票選擇高鐵還是火車是不同的。對于選擇高鐵的乘客來說，時間越長，對舒適程度越為看重；對于選擇火車的乘客來說，時間越長，就越不關心舒適程度。對于二者來說，時間越長，乘客會選擇較低的票價，并且所有乘客對于出行花費的時間都很重視。

希望能夠建立某種準則反映學生購票行為，對于學生購票行為進行綜合評價打分，根據CCA分析之后得到的函數表達式的系數，對系數進行AHP層次分析法，得到的系數如表2所示。

表2 AHP權重系數

運用兩種方法檢驗 AHP 層次分析法可行性。

方案1：根據一致性指標公式進行判斷。由于共有 8 個自變量，故 n=8。得到 CI=0.130 6，非常接近 0。隨機相關一致性 RI=1.41，CR=0.092 6<0.1，AHP 層次分析法結果滿足檢驗。

方案2：用模糊綜合評價法進行分析。首先，確定因素集，也就是評價指標，根據CCA分析結果，選出4個主要因素進行模糊綜合評價。確定因素集，也就是評價指標U={行駛時間長度，購票價格，舒適程度，時間成本}，然后確定評語集V={非常重要，重要，一般，不太重要}。根據AHP層次分析確認各因素權重，確定模糊綜合評價矩陣對各因素做出評價，進行矩陣合成運算。最終求得在顧客購票行為因素中，行駛時間長度因素非常重要，購票價格因素重要，時間成本一般，舒適程度因素不太重要。

4 模型的評價

C-SVM 是一種有堅實理論基礎的新穎的小樣本學習方法。對于本文中的樣本較少，邏輯數據和數值數據分布不清的問題，特別適用 SVM 模型進行求解。C-SVM模型的最終決策函數只由少數的支持向量所確定，計算的復雜性取決于支持向量的數目，而不是樣本空間的維數，降低了過擬合的風險。但是SVM也有不足之處，SVM 算法對大規模訓練樣本難以實施。

經典的支持向量機算法只給出了二類分類的算法，而在數據挖掘的實際應用中，一般要解決多類的分類問題。只能通過多個二類支持向量機的組合來解決，勢必會增加誤差的累計，最終使得預測結果偏差較大。