衛星影像在軌定位解算模型構建
丁榮莉,謝寶蓉,王 琰,朱浩文,張夢琪
(上海航天技術研究院,上海 201109)
0 引言
隨著遙感技術的發展,衛星影像分辨率不斷提高,已經可以達到數十米甚至一米之內[1],影像分辨率的提高利于定位解算技術發展的同時也對定位精度提出更嚴苛的需求。在軌定位解算技術在無需地面處理的情況下,可以實時提供偵測目標的物理位置信息以實現對動、靜目標的定位,可以為一些相關領域的軍事及民用項目提供有力的技術支持,如在民用上可以實現漁船等目標的實時跟蹤,從而保障出現事故時可及時進行搜救,在軍事上可用于對典型目標如船艦、潛艇等定位以及敏感運動目標的運動軌跡跟蹤和行為意圖的預判,及時有效地建立防御以保障國家領土安全[2-4]。國外定位解算技術相對成熟,文獻[5]詳細介紹了遙感衛星成像模型中涉及到的主要坐標系并建立了嚴格成像幾何模型。劉世杰[6]探討了高分辨率衛星遙感影像的各種成像模型,包括嚴格物理成像模型和有理函數模型等。文獻[7]分析了星載線陣CCD傳感器嚴格成像模型的一般建立方法與過程,針對不同的典型高分辨率遙感衛星傳感器特點,分別給出了3種改化的嚴格成像模型。
傳統衛星支持作業任務時通常由星上數據獲取、星地數傳、地面處理和信息分發等環節構成,有效信息到達作戰單元的延遲過長,難以滿足高動態戰場環境感知及戰術作戰情報信息支持需求。因此,亟需開展在軌處理技術研究以保障信息的實效性。現階段我國定位解算多是在地面處理計算,而星上在軌定位解算技術發展仍比較空白。本文著重分析了章動歲差、自轉和極移對定位精度的影響,并在此基礎上優化得到在軌實時定位模型,其算法復雜度相比嚴格物理成像模型大大降低,符合在軌實現的硬件要求。
1 嚴格物理成像模型
衛星影像拍攝時刻的像點、投影中心和地面物點這3點滿足共線方程,依據3點共線可建立嚴格物理成像模型[8-9]。模型還涉及到一系列航天坐標系及其相互轉換,需要依次建立WGS84坐標系[10]、J2000坐標系[11]、軌道坐標系、本體坐標系、相機坐標系和焦平面坐標系[12]。通過坐標系間的轉換,將影像坐標與地面坐標歸一到同一參考系下,坐標系變換框圖如圖1所示。
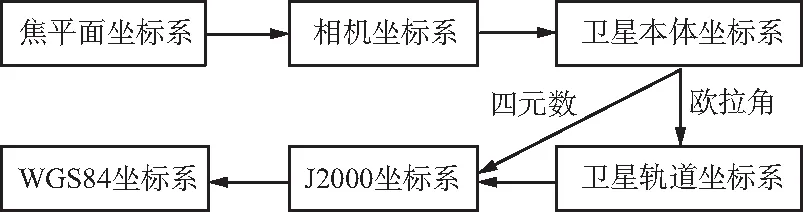
圖1 航天坐標系變換框圖Fig.1 Transformation block diagram of space coordinate systems
由以上可得嚴格物理成像模型表達式:
(1)
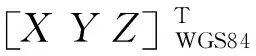
2 星上幾何成像模型構建
星上存儲資源緊張且感興趣目標點定位解算實時性要求較高,而嚴格物理成像模型涉及大量的三角函數運算和矩陣變換,計算資源消耗大且計算耗時長,因此需要對嚴格物理成像模型進行優化從而得到適用于星上處理的幾何成像模型。

(2)
b3=-s/|s|,
(3)
b2=b3×v/|b3×v|,
(4)
b1=b2×b3,
(5)
式中,s為J2000坐標系中的衛星位置矢量;v為J2000坐標系中的衛星速度矢量。
J2000坐標系到WGS84坐標系的變換矩陣為[14]:
(6)
式中,W(t)為極移矩陣;R(t)為地球自轉矩陣;Q(t)章動歲差矩陣。
GPS下傳的衛星軌道數據常為WGS84坐標系下的速度和位置,進行定位解算時首先需將WGS84坐標系下的速度和位置轉換為J2000坐標系下的速度和位置,即:
sJ2000=[W(t)·R(t)·Q(t)]T·sWGS84=
(7)
vJ2000=QT(t)·RT(t)[WT(t)·vWGS84+we×
(WT(t)·sWGS84)]=
(WT(t)·sWGS84),
(8)
式中,we=7.292×10-5(1-LOD/86 400)。
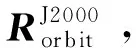
(9)
(10)
由以上可知,定位時J2000坐標系到WGS84坐標系的變換矩陣,以及軌道坐標系到J2000坐標系的變換矩陣表達式中都涉及章動歲差矩陣、地球自轉矩陣和極移矩陣及其逆矩陣的求解。而這3個矩陣求解時涉及的角度表達式系數多、運算量大、計算復雜。為降低模型運算量對它們展開具體分析。
2.1 章動歲差矩陣
在J2000坐標系轉WGS84坐標系過程中,若不考慮章動歲差影響,則其引起的誤差表達式為:
(11)
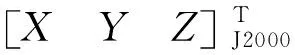
根據式(11)進行Matlab仿真得坐標轉換誤差,如圖2所示。
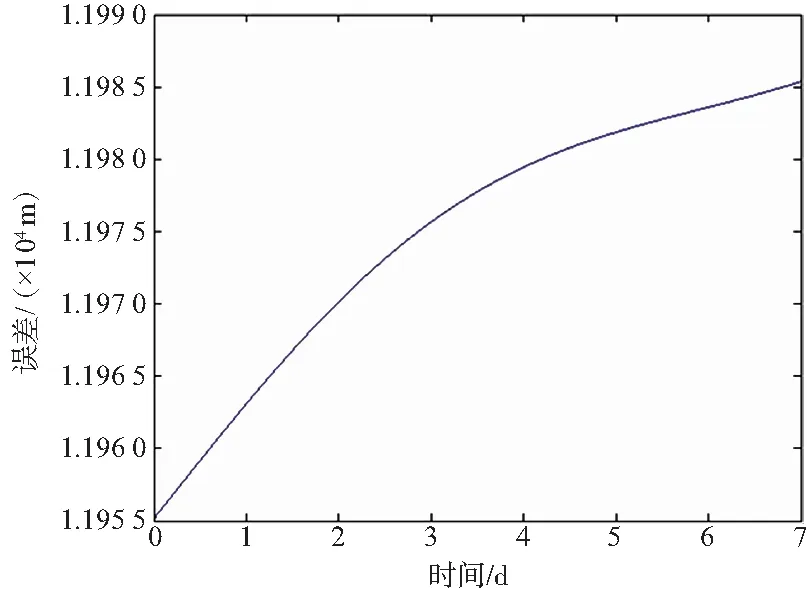
圖2 缺省章動歲差對坐標變換影響Fig.2 The effect of default nutation precession on coordinate transformation
由圖2可知,J2000坐標系轉WGS84坐標系的過程中,在7天觀測時間內,章動歲差對J2000坐標系轉WGS84坐標系產生的影響峰值超過11.986 km,且呈緩慢增長趨勢。故坐標系變換過程中缺省章動歲差對變換結果影響較大,不可忽略。
2.2 地球自轉矩陣
在J2000坐標系轉WGS84坐標系過程中若不考慮地球自轉影響,則其引起的誤差表達式為
(12)
式中,d(r)為有無地球自轉矩陣引起的距離誤差;R(t)為地球自轉矩陣。
根據式(12)進行Matlab仿真得坐標轉換誤差,如圖3所示。
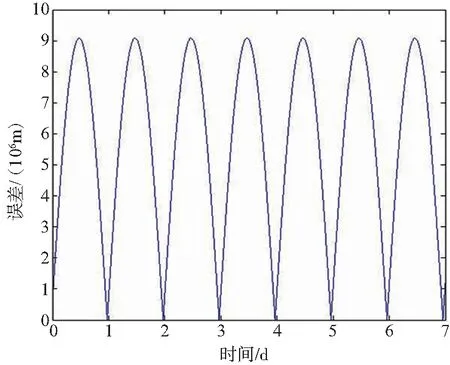
圖3 缺省地球自轉對坐標變換影響Fig.3 The effect of default earth rotation on coordinate transformation
由圖3可知,J2000坐標系轉WGS84坐標系過程中,在7天觀測時間范圍內,地球自轉對J2000坐標系轉WGS84坐標系產生的影響峰值超過9 000 km。坐標系變換過程中缺省地球自轉矩陣對變換結果影響顯著,不可缺省自轉構成的變換矩陣。
2.3 極移矩陣
在J2000坐標系轉WGS84坐標系過程中若不考慮極移矩陣影響,則其引起的誤差表達式為
(13)
式中,d(r)為有無極移矩陣引起的距離誤差;W(t)為極移矩陣。
根據式(13)進行Matlab仿真得坐標轉換誤差,如圖4所示。
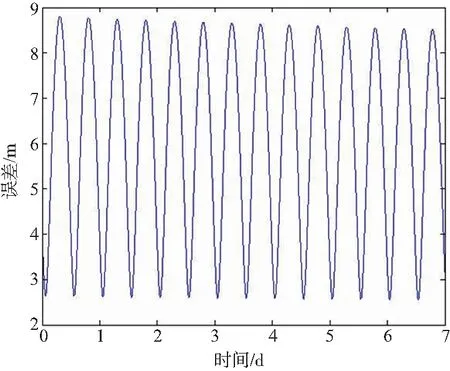
圖4 缺省極移對坐標變換影響Fig.4 The effect of default polar shift on coordinate transformation
由圖4可知,J2000坐標系轉WGS84坐標系過程中,在7天觀測時間范圍內,極移矩陣對J2000坐標系轉WGS84坐標系產生的影響峰值不超過9 m。極移影響較小,為降低算法復雜度可以缺省極移矩陣。
根據以上分析可知,極移矩陣對衛星定位精度影響較小,故可忽略極移影響。將焦平面坐標系下的像素坐標變換到衛星本體坐標系下表示為[X1,Y1,Z1],其表達式為:
(14)
將式(4)帶入嚴格物理成像模型:

(15)
按式(15)進行定位時不僅要求解J2000坐標系到WGS84坐標系的變換矩陣,還需求解其逆矩陣,而章動歲差矩陣和地球自轉矩陣和極移矩陣求解復雜,為進一步降低運算量,依據三階正交矩陣的分配率[15],若|R|=1,則R(B×C)=(RB)×(RC),對模型進行優化。優化后得星上幾何成像模型表達式為:
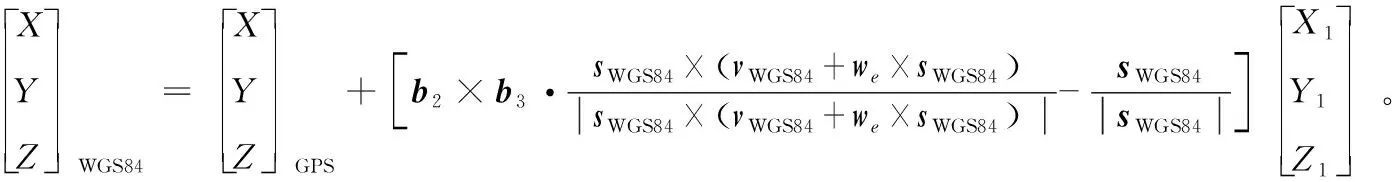
(16)
星上幾何成像模型不需要求解J2000坐標系轉WGS84坐標系的變換矩陣,且簡化了本體坐標系到J2000坐標系變換矩陣形式,大大降低了模型復雜度,為星上在軌處理奠定了基礎。
3 實驗仿真驗證
為驗證所構建星上幾何成像模型的準確性,采用衛星拍攝的迪拜影像和其對應的GPS接收機輸出的軌道位置速度信息以及星敏感器和陀螺組合定姿輸出的姿態信息進行仿真分析。迪拜影像成像時間為相對時間,GPS接收機輸出WGS84坐標系下的位置和速度,姿態數據以歐拉角形式給出。在影像上隨機選取若干像素點進行定位解算,并將定位解算結果與其對應的谷歌地圖真實經緯度進行比較求解誤差,其結果如表1所示。
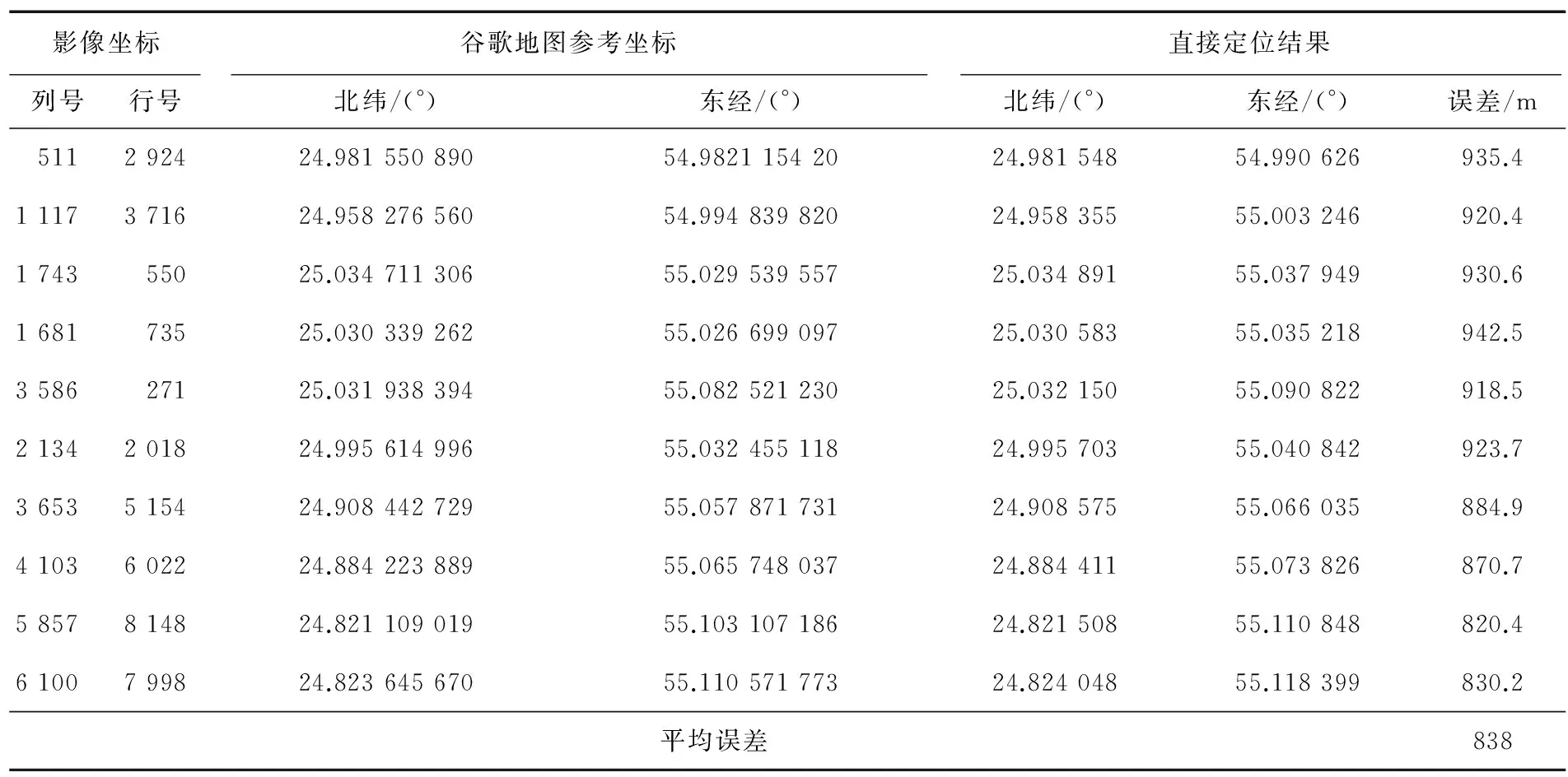
表1 圖像直接定位結果Tab.1 Direct image location results
由表1可知,影像的直接定位結果誤差均值為838 m,影像各像素點的誤差值沿均值分布,可以證實星上幾何成像模型構建的準確性。
4 結束語
為節約星地傳輸資源和保障定位解算的實時性,深入理解嚴格物理成像模型的原理,分析了章動歲差、地球矩陣和極移對坐標變換的影響,其中極移矩陣對坐標變換影響低于10 m,極移矩陣可忽略不計。再依據三階正交矩陣的分配率對嚴格物理成像模型表達式進行優化從而得到星上幾何成像模型。星上幾何成像模型避免了復雜的J2000坐標系到WGS84坐標系的變換矩陣求解,算法復雜度明顯降低。同時經衛星拍攝的影像進行定位解算驗證,未定標定位誤差均值為838 m,星上幾何成像模型的構建準確。雖然直接定位誤差結果相對理想,但仍不能滿足高分辨率衛星定位精度的需求,因此定位解算的在軌定標技術是未來需要繼續研究的課題。

